Guia de Intervenção
Plano de Aula
Plano de aula: Estratégias de multiplicação com número decimal.
Plano 2 de uma sequência de 5 planos. Veja todos os planos sobre Descobrindo estratégias de cálculo com números racionais
Por: Joel Luiz Pereira
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Joel Luiz Pereira
Mentora: Débora Vieira de Moraes
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF07MA08 - Compreender e utilizar a multiplicação e a divisão de números racionais, a relação entre elas e suas propriedades operatórias.
Conhecimentos que a turma deve dominar:
- Operações de multiplicação com números decimais (Unidade NOVA ESCOLA: MAT6_06NUM; Base Nacional: EF06MA10)
- Operações de multiplicação com números negativos (Unidade NOVA ESCOLA: MAT7_04NUM; Base Nacional: EF07MA04)
- Estimativas e cálculo mental (Unidade NOVA ESCOLA: MAT6_04NUM; Base Nacional: EF06MA03)
Objetivos específicos
- Operar multiplicações envolvendo números decimais positivos e negativos.
- Estabelecer estratégias para cálculo de multiplicações.
- Desenvolver habilidade de cálculo mental, propondo estimativas.
Conceito-chave
Multiplicação de números decimais.
Recursos necessários
- Atividades impressas em folhas, coladas no caderno ou não.
- Calculadoras.
- Projetor multimídia (caso não se utilize impressões).
Habilidades BNCC:
Objetivos de aprendizagem
- Operar multiplicações envolvendo números decimais positivos e negativos.
- Estabelecer estratégias para cálculo de multiplicações.
- Desenvolver habilidade de cálculo mental, propondo estimativas.
Resumo da aula
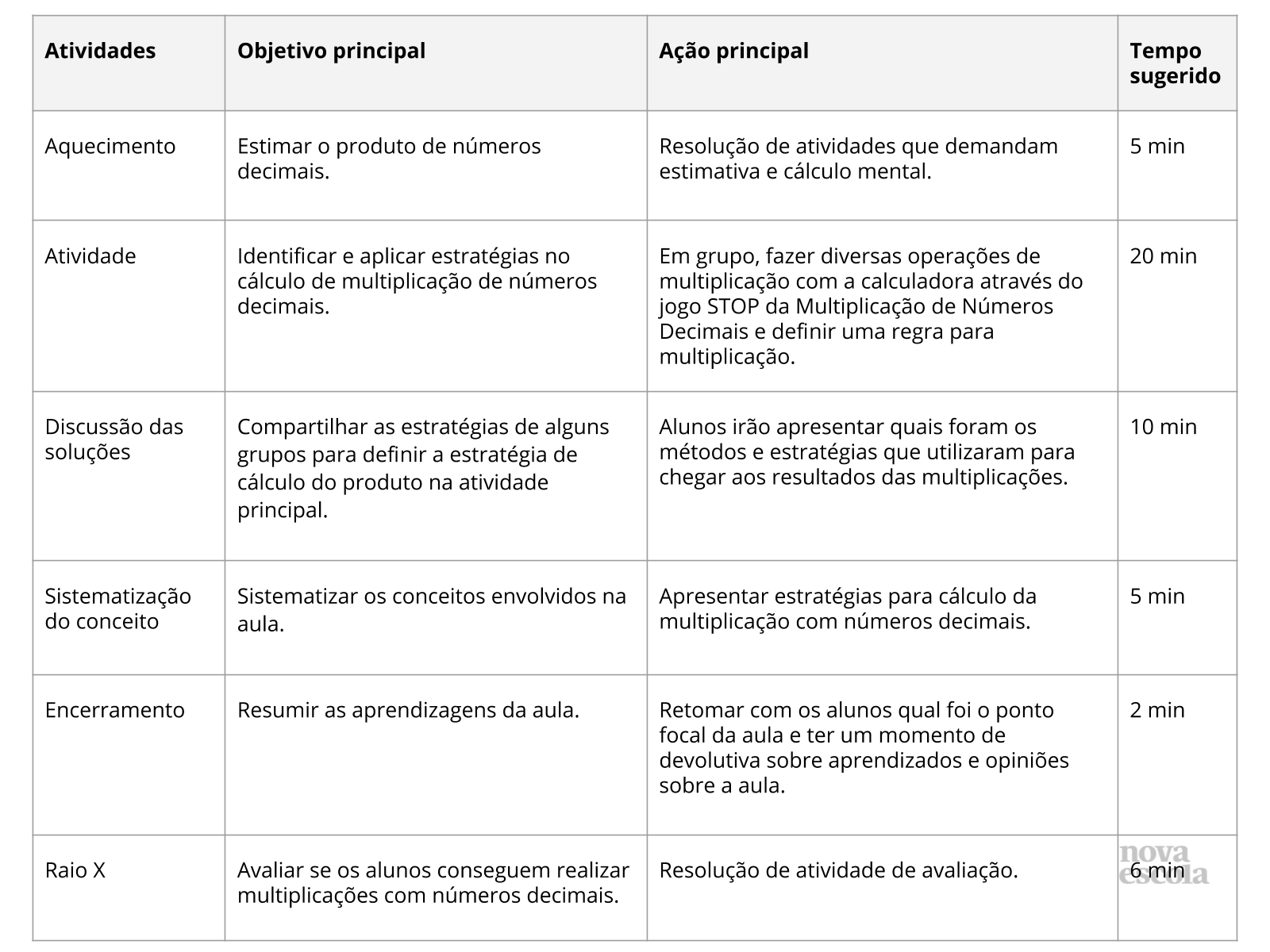
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma, informando aos alunos que irão atingir o objetivo da aula a partir de uma atividade lúdica. Questione a eles quais são as estratégias de cálculo que possuem para realizar uma multiplicação.
Propósito: Compartilhar o objetivo da aula.
Aquecimento

Tempo sugerido: 5 minutos.
Orientação: Escolha alguns alunos para que digam quais estimativas de valor conseguem apontar para o produto da multiplicação. O valor deve ser maior que 90 (3 x 30) e menor do que 120 (3 x 40). Após estabelecido o valor estimado e tendo sido explicado pelos alunos seu método para alcançá-lo, deixe os alunos utilizarem seus métodos para encontrar o valor exato do produto. Peça então que comparem o produto da questão aos resultados das multiplicações propostas em cada item, garantindo que os alunos percebam que os algarismos do produto, assim como dos fatores, continuarão os mesmos, alterando apenas as casas decimais. Assim, explore com os alunos as formas e estratégias para alcançar os produtos.
Propósito: Estimar o produto de números decimais positivos e negativos.
Discuta com a turma:
- Quais os métodos para chegar à estimativa? E qual estratégia utilizada para resolver a multiplicação?
- Como posso saber qual o número inteiro mais próximo do produto de uma multiplicação que envolve números decimais?
- Como saber a quantidade de casas decimais que o produto irá ter?
- Como saber se o produto será positivo ou negativo?
Solução da atividade:
a) 10,8 b) -1,08 c) 0,108 d) -1,08
Atividade principal - parte I

Tempo sugerido: 5 minutos (slides 4 e 5).
Orientação:
- Antes de iniciar a atividade, leia a regra para os alunos e tenha certeza de que eles entenderam o desenvolvimento da atividade (para isso, questione os alunos e peça para que repitam o que deve ser feito). Explique que a atividade será dividida em 3 partes e que esta é a primeira parte.
- Após, separe-os em grupo previamente definidos com até 5 alunos (tenha em mente as habilidades de cada aluno) e, caso não seja possível imprimir, peça para que separem uma folha do caderno e copiem o modelo estabelecido (o plano traz uma sugestão de valores, mas pode ser alterado).
- Durante a atividade, garanta que os números indicados pelos alunos sejam números decimais negativos. Enquanto estiverem trabalhando em grupos, circule pela sala e averigue se todos os alunos estão realizando os cálculos na calculadora e se há algum equívoco sendo cometido. Geralmente alguns alunos não utilizam calculadora, então, caso haja necessidade de intervenção, analise se deve ser feita uma orientação específica ou para toda a sala. Também instigue que os membros do grupo troquem informações e conhecimento entre si.
Utilize o guia de intervenções para analisar as dificuldades e realizar intervenções.
Você pode fazer o download desta atividade para imprimir para os seus alunos aqui. A solução está disponível aqui.
Discuta com a turma:
- Discuta com um colega ao lado sobre as observações e cálculos que ele fez. Quais as semelhanças e diferenças entre suas observações?
Propósito: Identificar e aplicar estratégias no cálculo de multiplicação de números decimais positivos e negativos
Material complementar:
- Para aprofundar seu repertório de exercícios e estratégias envolvendo multiplicações com números decimais, acesse o site Khan Academy.
Atividade principal - parte I

Tempo sugerido: 5 minutos (slides 4 e 5).
Orientação:
- Antes de iniciar a atividade, leia a regra para os alunos e tenha certeza de que eles entenderam o desenvolvimento da atividade (para isso, questione os alunos e peça para que repitam o que deve ser feito). Explique que a atividade será dividida em 3 partes e que esta é a primeira parte.
- Após, separe-os em grupo previamente definidos com até 5 alunos (tenha em mente as habilidades de cada aluno) e, caso não seja possível imprimir, peça para que separem uma folha do caderno e copiem o modelo estabelecido (o plano traz uma sugestão de valores, mas pode ser alterado).
- Durante a atividade, garanta que os números indicados pelos alunos sejam números decimais negativos. Enquanto estiverem trabalhando em grupos, circule pela sala e averigue se todos os alunos estão realizando os cálculos na calculadora e se há algum equívoco sendo cometido. Geralmente alguns alunos não utilizam calculadora, então, caso haja necessidade de intervenção, analise se deve ser feita uma orientação específica ou para toda a sala. Também instigue que os membros do grupo troquem informações e conhecimento entre si.
Utilize o guia de intervenções para analisar as dificuldades e realizar intervenções.
Você pode fazer o download desta atividade para imprimir para os seus alunos aqui. A solução está disponível aqui.
Discuta com a turma:
- Discuta com um colega ao lado sobre as observações e cálculos que ele fez. Quais as semelhanças e diferenças entre suas observações?
Propósito: Identificar e aplicar estratégias no cálculo de multiplicação de números decimais positivos e negativos
Material complementar:
- Para aprofundar seu repertório de exercícios e estratégias envolvendo multiplicações com números decimais, acesse o site Khan Academy.
Atividade principal - parte II

Tempo sugerido: 7 minutos.
Orientação:
- Finalize a parte I da atividade e explique aos alunos que na parte II serão feitas observações e anotações.
- As observações e anotações deverão ser feitas no caderno (para isso, os alunos deverão consultar a folha de anotações utilizadas na parte I da atividade)
- Se os alunos não conseguirem perceber regularidades para multiplicação de números decimais através dos cálculos realizados na parte I da atividade, você pode dedicar uma segunda rodada de cálculos, garantindo que eles façam observações e anotações.
- Após um breve momento de observações e anotações (até 3 minutos), utilize as perguntas do slide para ajudar os alunos a verificar regularidades.
Utilize o guia de intervenções para analisar as dificuldades e realizar intervenções.
Você pode fazer o download desta atividade para imprimir para os seus alunos aqui. A solução está disponível aqui.
Discuta com a turma:
- Discuta com um colega ao lado sobre as observações que ele fez. Quais as semelhanças e diferenças entre suas observações?
Propósito: Identificar e aplicar estratégias no cálculo de multiplicação de números decimais positivos e negativos
Material complementar:
- Para aprofundar seu repertório de exercícios e estratégias envolvendo multiplicações com números decimais, acesse o site Khan Academy.
Atividade principal - parte III

Tempo sugerido: 8 minutos.
Orientação:
- Explique aos alunos que agora terão de definir estratégias para o cálculo dos produtos das multiplicações e aplicar essa estratégia em alguma multiplicação que antes tinha sido efetuada pela calculadora. Garanta que todos os alunos entenderam a transição entre a atividade.
- A folha de anotações utilizadas na parte I da atividade serve como consulta para o aluno verificar se os resultados estão de acordo com as respostas já encontradas anteriormente pela calculadora.
- Se o professor achar melhor, pode ser indicado um novo número e os alunos terão de definir a regra e realizar as multiplicações corretamente com base nesse novo número indicado.
- Ganha o grupo que definir a regra primeiro e aplicá-la corretamente às multiplicações.
- Enquanto estiverem trabalhando em grupos, circule pela sala e averigue se todos os alunos estão se esforçando e realizando a atividade. Também sugira que alguns grupos transformem o número decimal em fração decimal, para ter diversidade nas soluções apresentadas (pergunte a um ou dois grupos: “E se transformássemos os números decimais em fração? Vocês poderiam tentar e verificar se daria certo?”)
- Para engajamento da turma, você pode providenciar alguma premiação simbólica para o grupo que definir primeiro a regra de multiplicação e conseguir aplicá-la.
Utilize o guia de intervenções para analisar as dificuldades e realizar intervenções.
Você pode fazer o download desta atividade para imprimir para os seus alunos aqui. A solução está disponível aqui.
Propósito: Identificar e aplicar estratégias no cálculo de multiplicação de números decimais positivos e negativos.
Material complementar:
- Para aprofundar seu repertório de exercícios e estratégias envolvendo multiplicações com números decimais, acesse o site Khan Academy.
Discussão das soluções
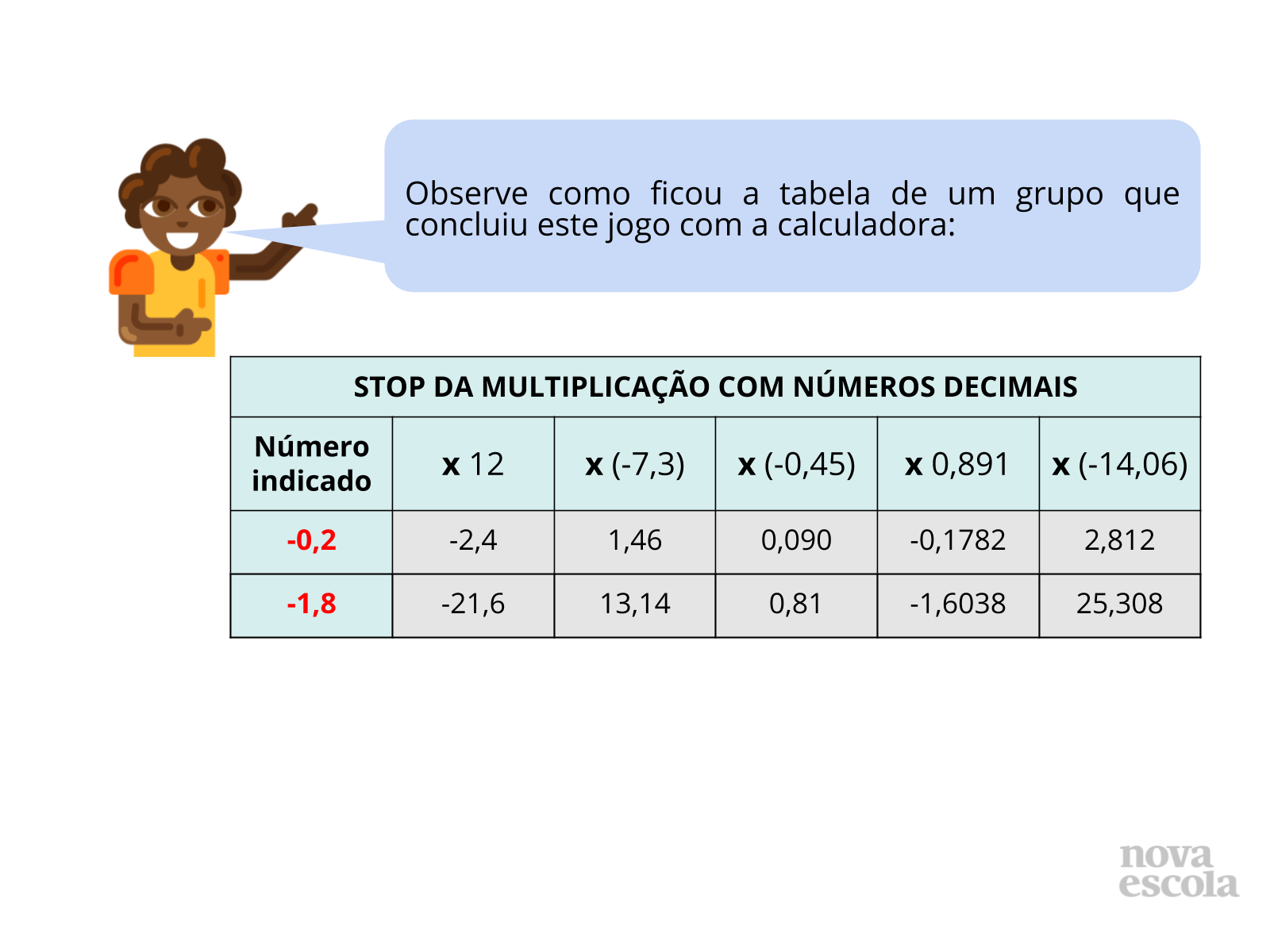
Tempo sugerido: 10 minutos (slides 8 a 10)
Orientação: Baseado nas observações que você fez durante a atividade, escolha alguns alunos para compartilharem as estratégias utilizadas na resolução da atividade e quais regras foram definidas a partir dessas estratégias. Sempre questione aos demais alunos se alguém resolveu do mesmo modo e por quê eles resolveram assim. Apenas depois das interações da turma e discussões, caso seja necessário, passe para esta série de slides, a fim de apresentar as alunos as regras definidas em cada caso (tanto na resolução decimal como fracionária). Vale ressaltar que, dado o fato que as respostas serão de acordo com os números indicados pelos alunos, o momento de discussão das soluções deve priorizar totalmente as respostas dadas em sala. Utilize o tópico “Discuta com a turma” para explorar as estratégias e fazer com que os alunos decidam quais serão as estratégias utilizadas por eles. Caso não haja projetor, você pode reproduzir as estratégias para cálculo das multiplicações no quadro.
Propósito: Fazer com que os alunos compartilhem as estratégias utilizadas na multiplicação de números decimais.
Discuta com a turma:
- Por que podemos utilizar a estratégia de transformar os números decimais em fração na resolução deste exercício? Qual a vantagem de adotá-la?
- Por que podemos utilizar a estratégia de continuar utilizando os números decimais nas multiplicações? Quais cuidados temos de tomar ao utilizar essa estratégia?
- Quais outras estratégias temos na multiplicação de números decimais?
- Nos casos de multiplicação de um número inteiro por um número decimal, quais estratégias podemos utilizar que difere das já relatadas? (neste momento, espera-se que seja apresentada a soma de parcelas iguais)
- Se há diversas estratégias de resolução, por que preferimos utilizar a convencional (número em sua forma decimal)? Quais fatores positivos temos ao adotá-la?
Discussão das soluções

Tempo sugerido: 10 minutos (slides 8 a 10)
Orientação: Baseado nas observações que você fez durante a atividade, escolha alguns alunos para compartilharem as estratégias utilizadas na resolução da atividade e quais regras foram definidas a partir dessas estratégias. Sempre questione aos demais alunos se alguém resolveu do mesmo modo e por quê eles resolveram assim. Apenas depois das interações da turma e discussões, caso seja necessário, passe para esta série de slides, a fim de apresentar as alunos as regras definidas em cada caso (tanto na resolução decimal como fracionária). Vale ressaltar que, dado o fato que as respostas serão de acordo com os números indicados pelos alunos, o momento de discussão das soluções deve priorizar totalmente as respostas dadas em sala. Utilize o tópico “Discuta com a turma” para explorar as estratégias e fazer com que os alunos decidam quais serão as estratégias utilizadas por eles. Caso não haja projetor, você pode reproduzir as estratégias para cálculo das multiplicações no quadro.
Propósito: Fazer com que os alunos compartilhem as estratégias utilizadas na multiplicação de números decimais.
Discuta com a turma:
- Por que podemos utilizar a estratégia de transformar os números decimais em fração na resolução deste exercício? Qual a vantagem de adotá-la?
- Por que podemos utilizar a estratégia de continuar utilizando os números decimais nas multiplicações? Quais cuidados temos de tomar ao utilizar essa estratégia?
- Quais outras estratégias temos na multiplicação de números decimais?
- Nos casos de multiplicação de um número inteiro por um número decimal, quais estratégias podemos utilizar que difere das já relatadas? (neste momento, espera-se que seja apresentada a soma de parcelas iguais)
- Se há diversas estratégias de resolução, por que preferimos utilizar a convencional (número em sua forma decimal)? Quais fatores positivos temos ao adotá-la?
Discussão das soluções

Tempo sugerido: 10 minutos (slides 8 a 10)
Orientação: Baseado nas observações que você fez durante a atividade, escolha alguns alunos para compartilharem as estratégias utilizadas na resolução da atividade e quais regras foram definidas a partir dessas estratégias. Sempre questione aos demais alunos se alguém resolveu do mesmo modo e por quê eles resolveram assim. Apenas depois das interações da turma e discussões, caso seja necessário, passe para esta série de slides, a fim de apresentar as alunos as regras definidas em cada caso (tanto na resolução decimal como fracionária). Vale ressaltar que, dado o fato que as respostas serão de acordo com os números indicados pelos alunos, o momento de discussão das soluções deve priorizar totalmente as respostas dadas em sala. Utilize o tópico “Discuta com a turma” para explorar as estratégias e fazer com que os alunos decidam quais serão as estratégias utilizadas por eles. Caso não haja projetor, você pode reproduzir as estratégias para cálculo das multiplicações no quadro.
Propósito: Fazer com que os alunos compartilhem as estratégias utilizadas na multiplicação de números decimais.
Discuta com a turma:
- Por que podemos utilizar a estratégia de transformar os números decimais em fração na resolução deste exercício? Qual a vantagem de adotá-la?
- Por que podemos utilizar a estratégia de continuar utilizando os números decimais nas multiplicações? Quais cuidados temos de tomar ao utilizar essa estratégia?
- Quais outras estratégias temos na multiplicação de números decimais?
- Nos casos de multiplicação de um número inteiro por um número decimal, quais estratégias podemos utilizar que difere das já relatadas? (neste momento, espera-se que seja apresentada a soma de parcelas iguais)
- Se há diversas estratégias de resolução, por que preferimos utilizar a convencional (número em sua forma decimal)? Quais fatores positivos temos ao adotá-la?
Sistematização do conceito
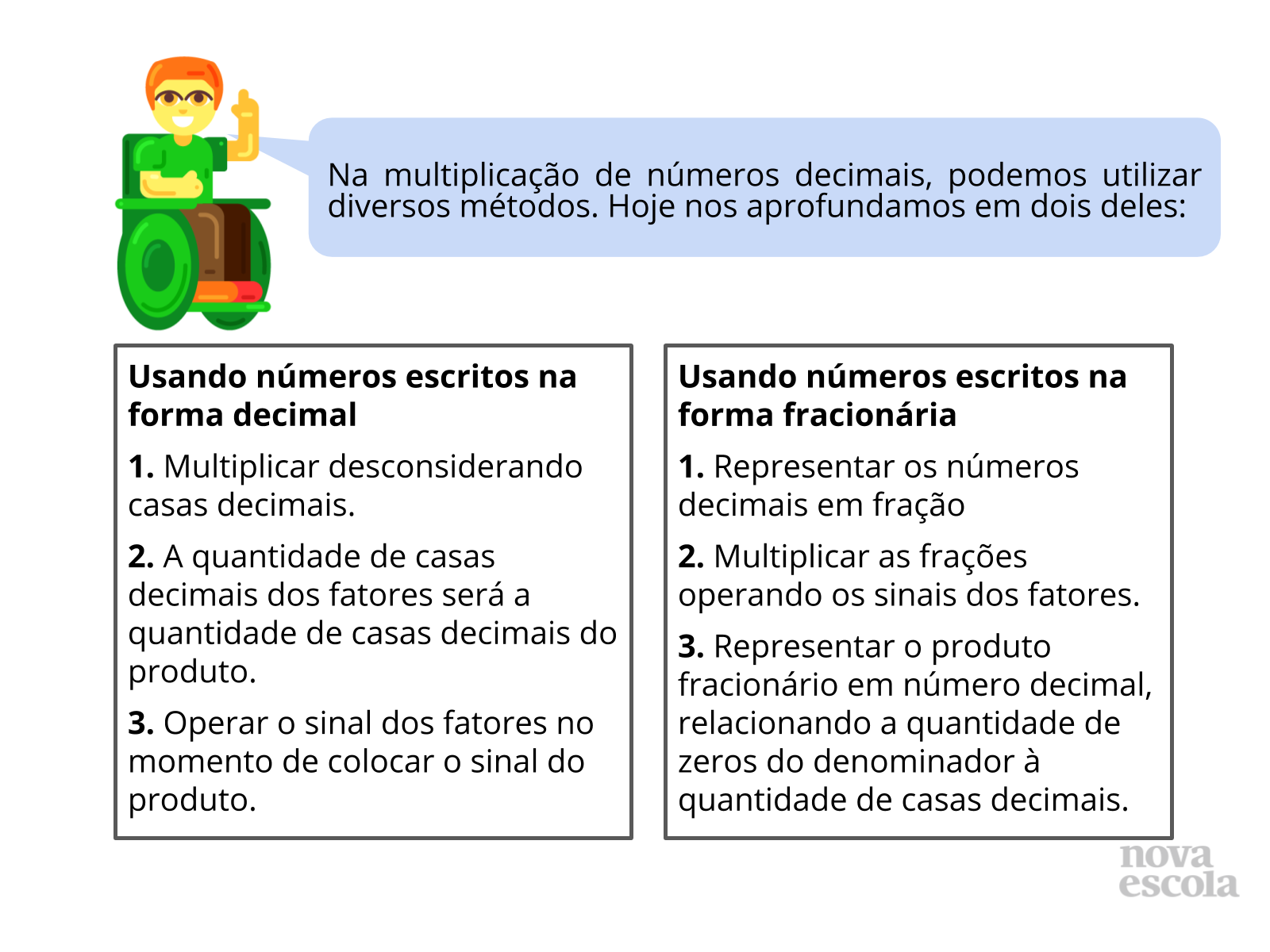
Tempo sugerido: 5 minutos
Orientação: Discuta com a turma sobre os diferentes métodos e estratégias de encontrar o produto de uma multiplicação, tendo certeza de que eles consigam compreender as vantagens e desvantagens de cada método. Neste momento, o aluno deve ter clareza de como se dá a aplicação de cada método, portanto, enfoque o passo a passo utilizado em cada um.
Propósito: Sistematizar os conceitos da aula, apresentando a forma de comparar números racionais positivos e negativos, bem como ordená-los.
Discuta com a turma:
- Qual a vantagem de usarmos o método de transformação em fração? E o método convencional de multiplicação (número em forma decimal)?
- Durante a aula, quais erros cometemos no método da transformação em fração? O que esses erros nos ensinaram?
- Quais erros foram cometidos no método convencional (número em forma decimal)? O que podemos aprender a partir disso?
- Você ainda tem alguma dúvida sobre como aplicar algum dos métodos trabalhados nesta aula? Se sim, crie um exercício de multiplicação de números decimais e tente aplicar novamente este método.
Encerramento

Tempo sugerido: 2 minutos.
Orientação: Encerre a aula relembrando qual foi a aprendizagem adquirida pelos alunos e escolha 3 alunos que possam opinar sobre os seguintes tópicos:
- Você já tinha aprendido multiplicações nos anos anteriores. O que mudou e o que se manteve, quando consideramos números decimais?
- Descreva, detalhadamente, como um(a) colega resolveu as multiplicações de hoje. Como o método utilizado por ele/ela se parece com o seu? Em que eles se diferem?
- Como você e seu grupo se organizaram para resolver as multiplicações? Essa organização foi bem-sucedida? O que você aprendeu sobre trabalho em grupo hoje?
Propósito: Resumir as aprendizagens do dia e refletir sobre a aula.
Raio X
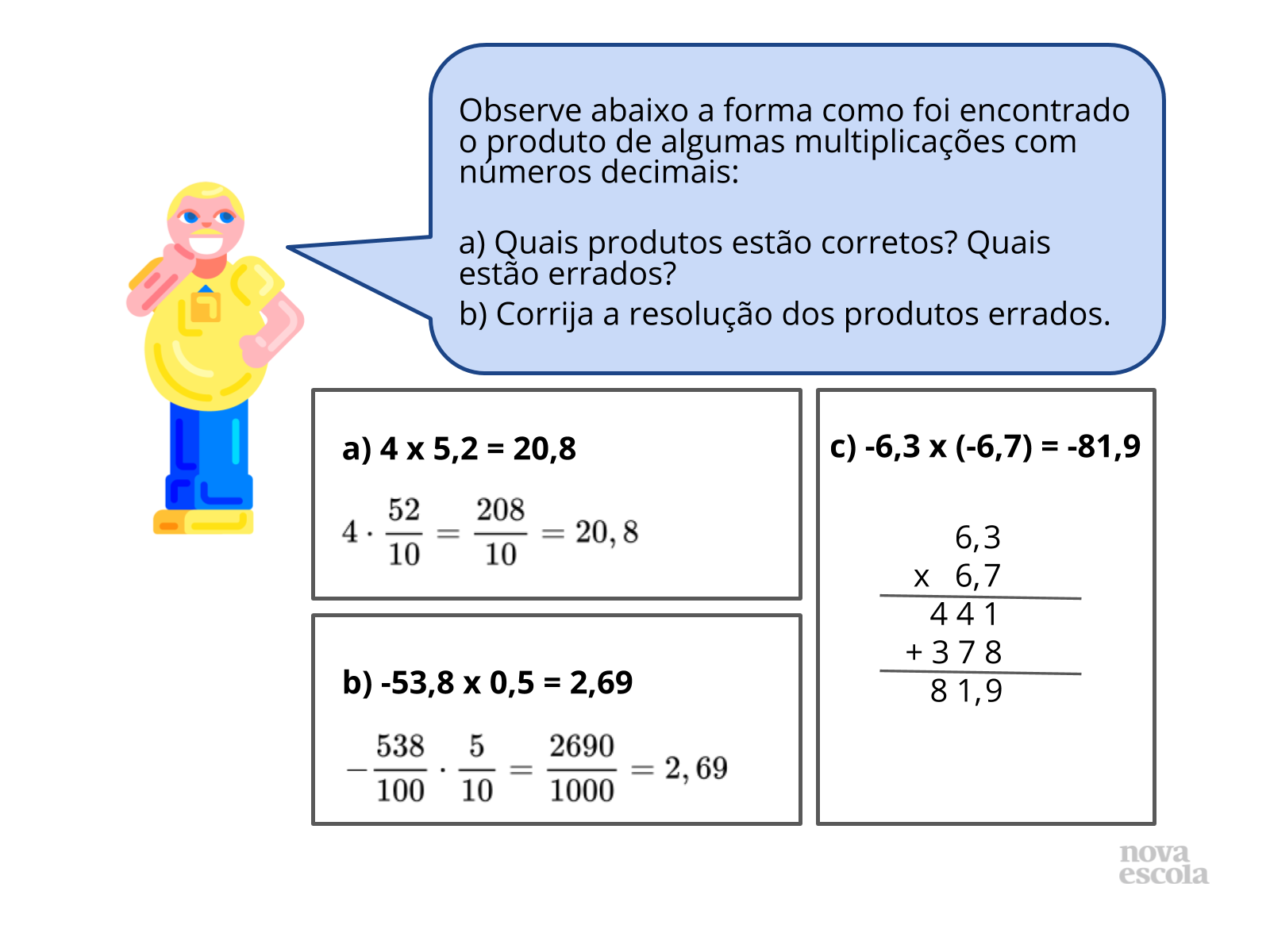
Tempo sugerido: 6 minutos.
Orientações: O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto. Assim, separe, para cada aluno, uma folha de papel recortada, onde os alunos terão de colocar o nome e responder a atividade. Você também pode pedir para que os alunos respondam as questões no caderno enquanto você circula pela sala anotando o desempenho da turma. No fim da aula , responda a atividade com os alunos e discuta com eles sobre como estimar o valor dos produtos.
Você pode projetar, passar no quadro ou fazer cópia da atividade para os alunos.
Você pode fazer o download desta atividade para imprimir para os seus alunos aqui.
Acesse aqui a resolução desta atividade.
Propósito: Avaliar quais as estratégias de cálculo utilizadas pelos alunos na obtenção do produto da multiplicação.
Discuta com a turma:
- Como podemos estimar o resultado do produto? A estimativa já demonstraria alguma questão que apresentou erros?
- Como podemos definir a quantidade de casas decimais que o produto irá conter? Essa estratégia já demonstraria alguma questão que apresentou erros?
Sugestão de adaptação para ensino remoto
Código do plano
MAT7_09NUM02
Recursos
- Necessários:
caderno
lápis
régua
grupo de alunos no WhatsApp
- Opcionais:
Google Sala de Aula
Meet
Vídeo : “Estratégias para multiplicar números decimais”- Khan Academy, disponível em: https://youtu.be/5H4iv_eQLrI acesso em 24 de jun 2020.
Jogo: “Jogo Números decimais” - Mathema.com, disponível em: https://mathema.com.br/jogos-e-atividades/numeros-decimais-e-calculadora-eu-quero-um/ acesso em 24 de jun 2020.
Para este plano, foque na etapa: Aquecimento
Aquecimento
Essa etapa é uma retomada ou “pontapé” inicial da aula. Comece perguntando para os alunos se eles sabem o que é uma estimativa. É importante que os alunos identifiquem o significado de estimar o produto de números decimais positivos e negativos. Para isso, inicie uma discussão via WhatsApp, estimulando a interação com e entre os estudantes, ou de maneira síncrona usando o Meet ou Zoom.
Atividade principal
A atividade é um jogo de Stop da multiplicação com números decimais.
Disponibilize o jogo por WhatsApp, Google Sala de Aula ou e-mail, para que os alunos possam jogar com seus familiares. Caso não seja possível o jogo, recomende aos alunos que acessem o site do Khan Academy e assistam ao video “Estratégias para multiplicar números decimais”.
Sistematização
Discuta com a turma sobre os diferentes métodos e estratégias de encontrar o produto de uma multiplicação, tendo certeza de que eles consigam compreender as vantagens e desvantagens de cada método. Disponibilize a imagem do slide via WhatsApp ou Google sala de aula para que os alunos façam a sistematização do conceito no caderno.
Raio X
O Raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto. Compartilhe a imagem do slide com os alunos usando o recurso de e-mail ou foto via WhatsApp. Peça que respondam à questão e lhe devolvam com ela resolvida. Analise as respostas, elabore devolutivas individuais sobre a atividade e reenvie com comentários para os alunos.
Convite às famílias
A participação das famílias no processo de aprendizagem é de grande importância para o aluno. Porém, ressaltamos que os pais não são professores de matemática e muitos estão ocupados com outras funções em casa. Portanto, indicamos a participação das famílias no compartilhamento e discussão de possíveis soluções para os problemas propostos ou interagindo com o aluno no momento do jogo da atividade principal. Outra sugestão para jogo em família é o Jogo dos números decimais, disponível no Mathema.com.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Joel Luiz Pereira
Mentora: Débora Vieira de Moraes
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF07MA08 - Compreender e utilizar a multiplicação e a divisão de números racionais, a relação entre elas e suas propriedades operatórias.
Conhecimentos que a turma deve dominar:
- Operações de multiplicação com números decimais (Unidade NOVA ESCOLA: MAT6_06NUM; Base Nacional: EF06MA10)
- Operações de multiplicação com números negativos (Unidade NOVA ESCOLA: MAT7_04NUM; Base Nacional: EF07MA04)
- Estimativas e cálculo mental (Unidade NOVA ESCOLA: MAT6_04NUM; Base Nacional: EF06MA03)
Objetivos específicos
- Operar multiplicações envolvendo números decimais positivos e negativos.
- Estabelecer estratégias para cálculo de multiplicações.
- Desenvolver habilidade de cálculo mental, propondo estimativas.
Conceito-chave
Multiplicação de números decimais.
Recursos necessários
- Atividades impressas em folhas, coladas no caderno ou não.
- Calculadoras.
- Projetor multimídia (caso não se utilize impressões).








