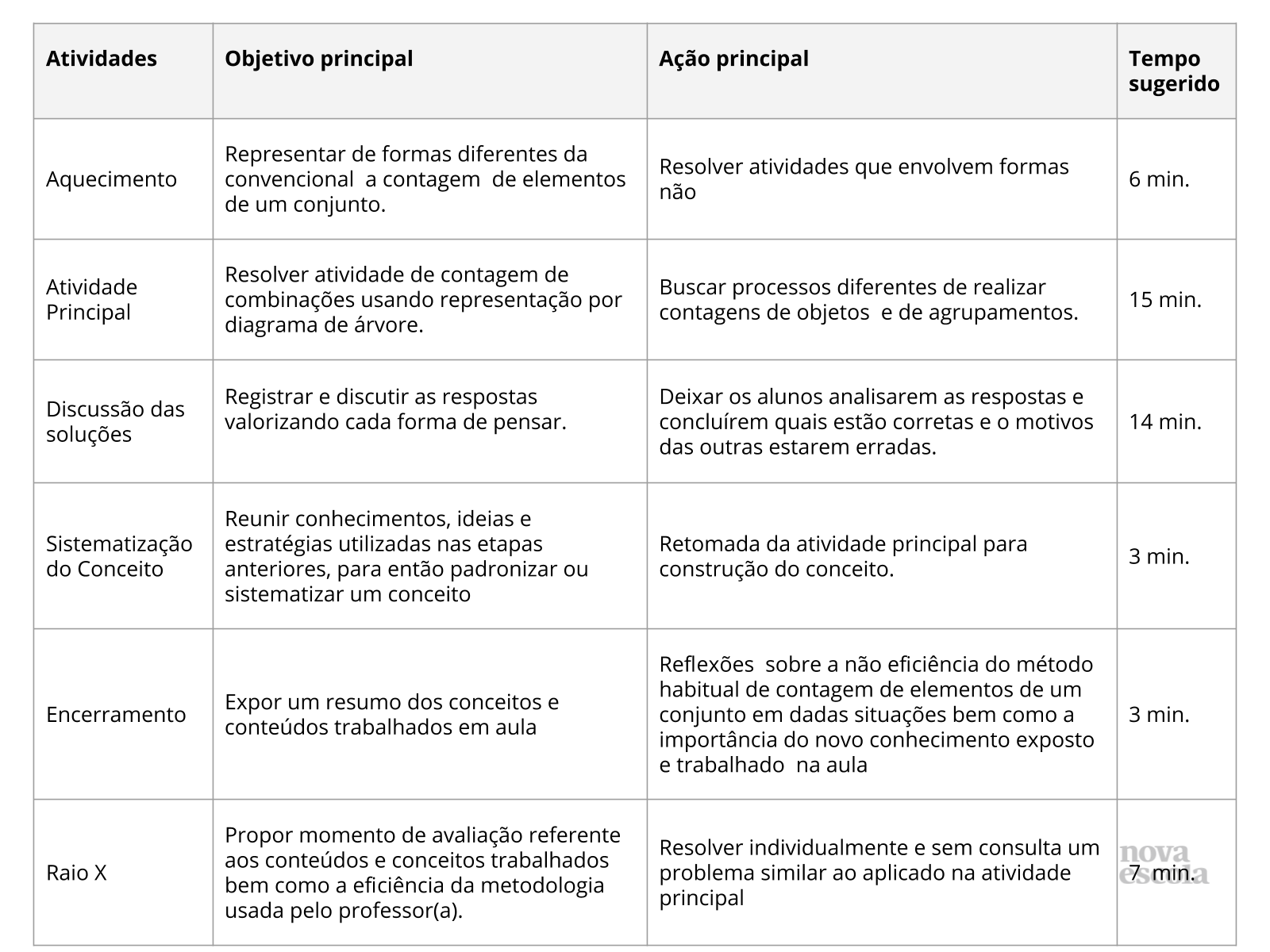
Aquecimento
Plano de Aula
Plano de aula: PRINCÍPIO MULTIPLICATIVO DA CONTAGEM E DIAGRAMAS DE ÁRVORE
Plano 1 de uma sequência de 5 planos. Veja todos os planos sobre Princípio multiplicativo da contagem
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Altamiro Marlon Ribeiro
Mentor: Amanda Ferreira Verardo Bilia
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
(EF08MA03): Princípio multiplicativo da contagem (resolução de problemas de contagem)
Conhecimento prévios:
Noção de organização triangular e construção de grafos e tabelas para representação de contagens.
Objetivos específicos
Elaborar e resolver problemas de contagem relacionando o Princípio Multiplicativo da Contagem com do Diagrama de árvore.
Conceito-chave
Contagem, princípio multiplicativo, diagrama de árvore
Recursos necessários
- Projetor (caso haja)
- Atividades impressas em folhas, coladas no caderno ou não.
- Folhas A4
- Lápis de cor e régua
Habilidades BNCC:
Objetivos de aprendizagem
Elaborar e resolver problemas de contagem relacionando o Princípio Multiplicativo da Contagem com do Diagrama de árvore.
Resumo da Aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo
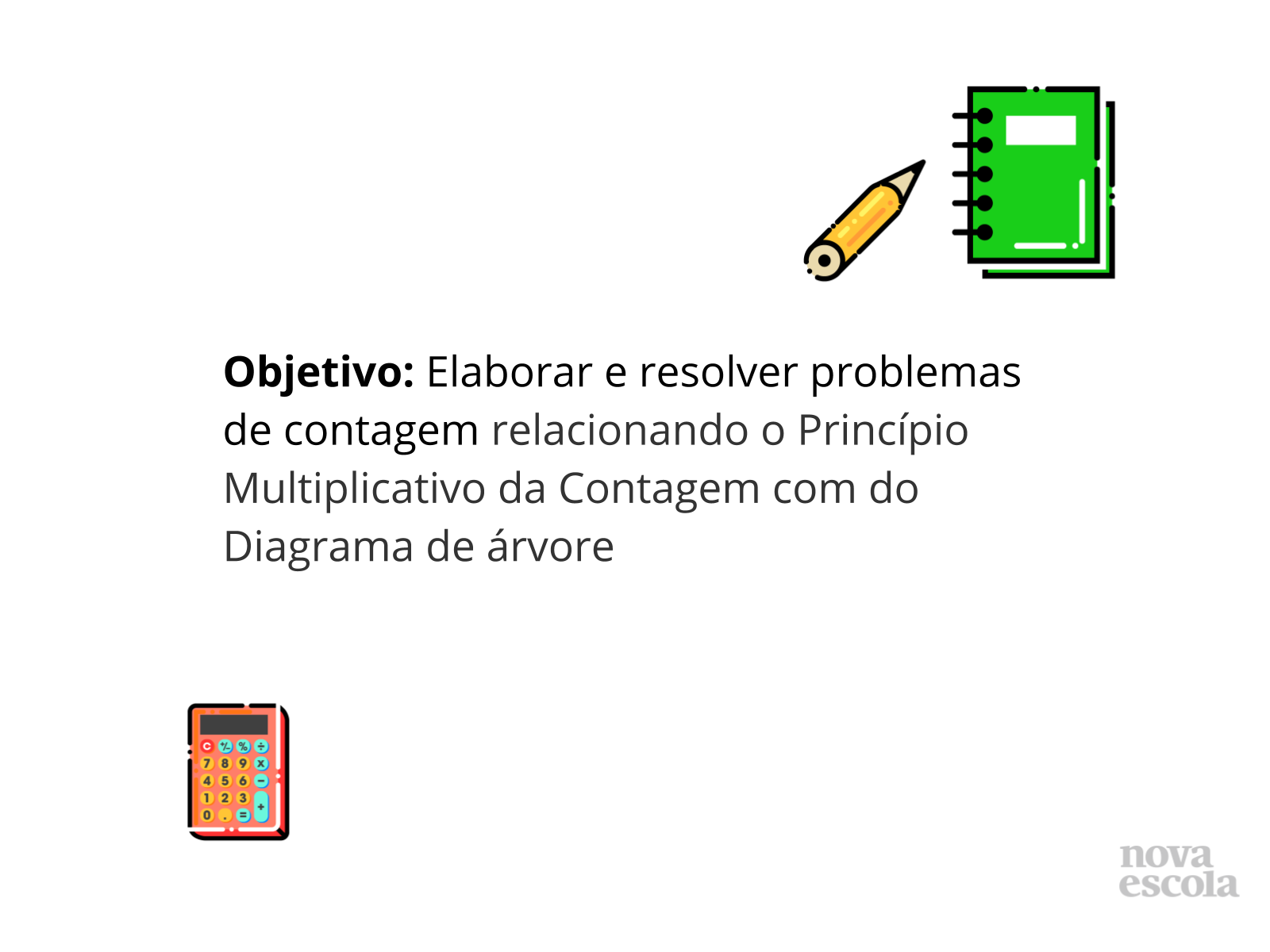
Tempo sugerido: 2 minutos
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Aquecimento
Tempo sugerido: 6 minutos (slides 3 a 7)
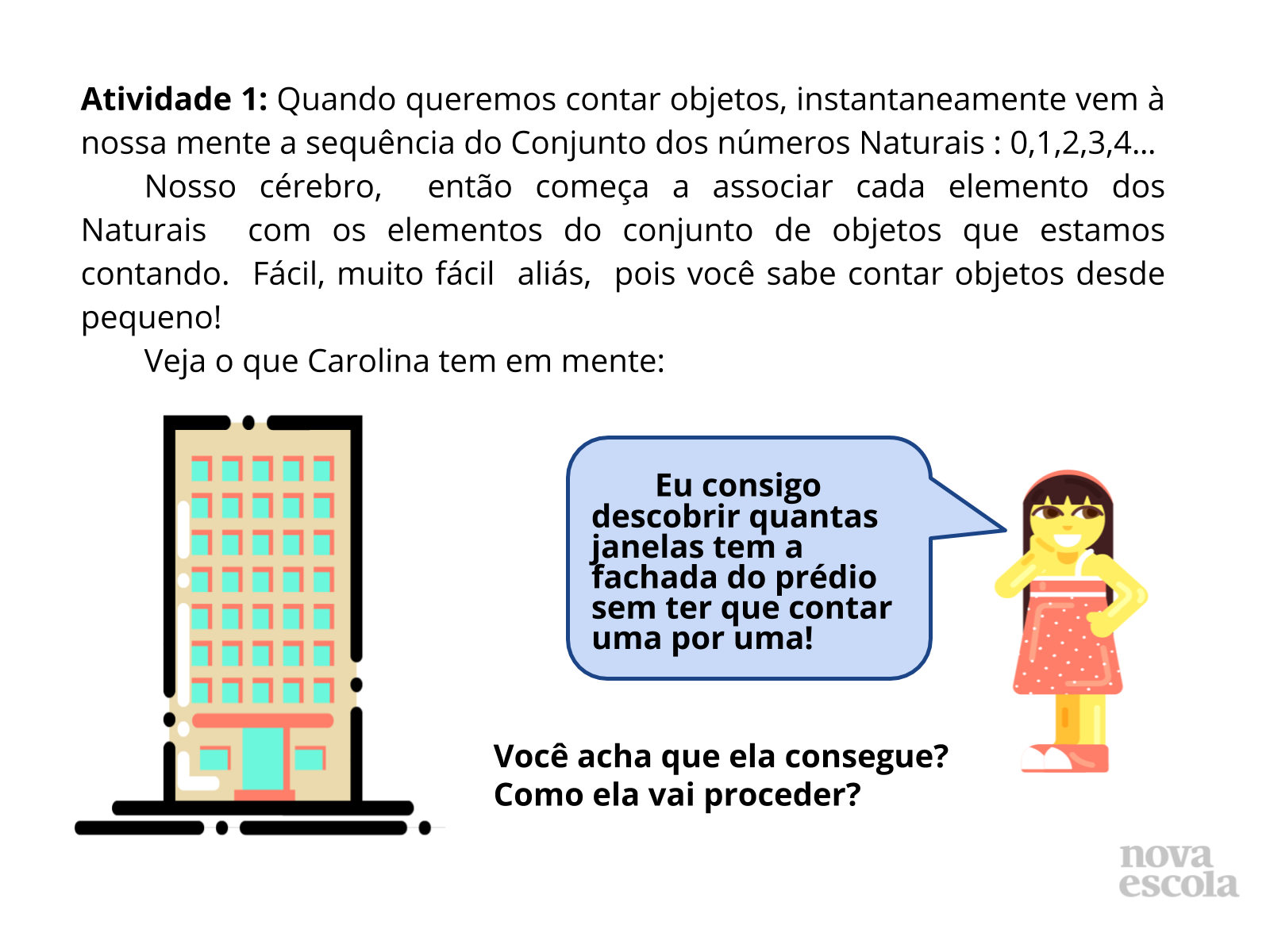
Orientação: Organize os alunos em duplas e de forma que não fiquem de costas uns para os outros. Projete o slide 3 e/ou distribua cópias impressas da atividade, leia com a turma e dê tempo para uma discussão sobre a forma com que a personagem irá proceder para determinar o número de janelas da fachada do prédio. Após ouvir algumas estratégias expostas pelos estudantes. Após esse momento, discuta com a turma o texto do slide 4 e peça para os estudantes exemplificarem outras situações em que podem fazer uma contagem de maneira indireta. Espera-se que eles, neste momento dêem exemplos de situações onde se aplica a “organização retangular” usada neste caso, ou em qualquer outro em que os objetos a serem contados possam ser dispostos em forma de retângulo. Não esqueça que podem surgir exemplos que se apliquem raciocínios muito diferentes destes, devem ser valorizados e discutidos, mas validados ou refutados com cautela, no decorrer da aula, quando surgirem oportunidades adequadas. Se for possível projete o slide 6 ou represente na lousa para que os estudantes vejam uma possibilidade para o diagrama de árvore. É possível que os estudantes já tenham percebido que para o total de possibilidades, basta multiplicar as opções de faces da moeda pelas opções de faces do dado, você pode até validar isso, mas chame atenção para o fato de não estarmos querendo apenas quantas possibilidades também queremos determinar quais são elas.
Propósito: Apresentar o enunciado da atividade e propor uma reflexão sobre métodos indiretos de contagem preparando o estudante para a resolução da atividade principal.
Discuta com a turma:
- É importante buscarmos métodos mais eficientes de realizar contagens por questões de praticidade pois, as vezes contar um por um demanda muito tempo e até mesmo erros na própria contagem?
- O que é um par ordenado?
Sugestão de resposta: par ordenado (x,y) é um par de elementos de conjuntos onde ordem de ocorrência desses elementos é relevante. Neste caso, x é o primeiro elemento e y é o segundo elemento.
- Pergunte por que, multiplicando 2 por 6 podemos obter a quantidade total de pares ordenados diferentes que se podem formar.
Sugestão de resposta: Para cada face da moeda que são 2, dispomos de 6 possibilidades para a face do dado. Portanto, Carolina tem 12 ( duas vezes seis) possibilidades para seus resultados.
- Qual a diferença entre perguntar quais e quantas possibilidades?
Sugestão de resposta: Quando a na pergunta aparece “quantas”, um número basta para responder a pergunta. Porém quando aparece “quais” é preciso representar uma a uma as possibilidades possíveis.
Materiais complementares para impressão:
Aquecimento

Tempo sugerido: 6 minutos (slides 3 a 7)
Orientação: Organize os alunos em duplas e de forma que não fiquem de costas uns para os outros. Projete o slide 3 e/ou distribua cópias impressas da atividade, leia com a turma e dê tempo para uma discussão sobre a forma com que a personagem irá proceder para determinar o número de janelas da fachada do prédio. Após ouvir algumas estratégias expostas pelos estudantes. Após esse momento, discuta com a turma o texto do slide 4 e peça para os estudantes exemplificarem outras situações em que podem fazer uma contagem de maneira indireta. Espera-se que eles, neste momento dêem exemplos de situações onde se aplica a “organização retangular” usada neste caso, ou em qualquer outro em que os objetos a serem contados possam ser dispostos em forma de retângulo. Não esqueça que podem surgir exemplos que se apliquem raciocínios muito diferentes destes, devem ser valorizados e discutidos, mas validados ou refutados com cautela, no decorrer da aula, quando surgirem oportunidades adequadas. Se for possível projete o slide 6 ou represente na lousa para que os estudantes vejam uma possibilidade para o diagrama de árvore. É possível que os estudantes já tenham percebido que para o total de possibilidades, basta multiplicar as opções de faces da moeda pelas opções de faces do dado, você pode até validar isso, mas chame atenção para o fato de não estarmos querendo apenas quantas possibilidades também queremos determinar quais são elas.
Propósito: Apresentar o enunciado da atividade e propor uma reflexão sobre métodos indiretos de contagem preparando o estudante para a resolução da atividade principal.
Discuta com a turma:
- É importante buscarmos métodos mais eficientes de realizar contagens por questões de praticidade pois, as vezes contar um por um demanda muito tempo e até mesmo erros na própria contagem?
- O que é um par ordenado?
Sugestão de resposta: par ordenado (x,y) é um par de elementos de conjuntos onde ordem de ocorrência desses elementos é relevante. Neste caso, x é o primeiro elemento e y é o segundo elemento.
- Pergunte por que, multiplicando 2 por 6 podemos obter a quantidade total de pares ordenados diferentes que se podem formar.
Sugestão de resposta: Para cada face da moeda que são 2, dispomos de 6 possibilidades para a face do dado. Portanto, Carolina tem 12 ( duas vezes seis) possibilidades para seus resultados.
- Qual a diferença entre perguntar quais e quantas possibilidades?
Sugestão de resposta: Quando a na pergunta aparece “quantas”, um número basta para responder a pergunta. Porém quando aparece “quais” é preciso representar uma a uma as possibilidades possíveis.
Aquecimento
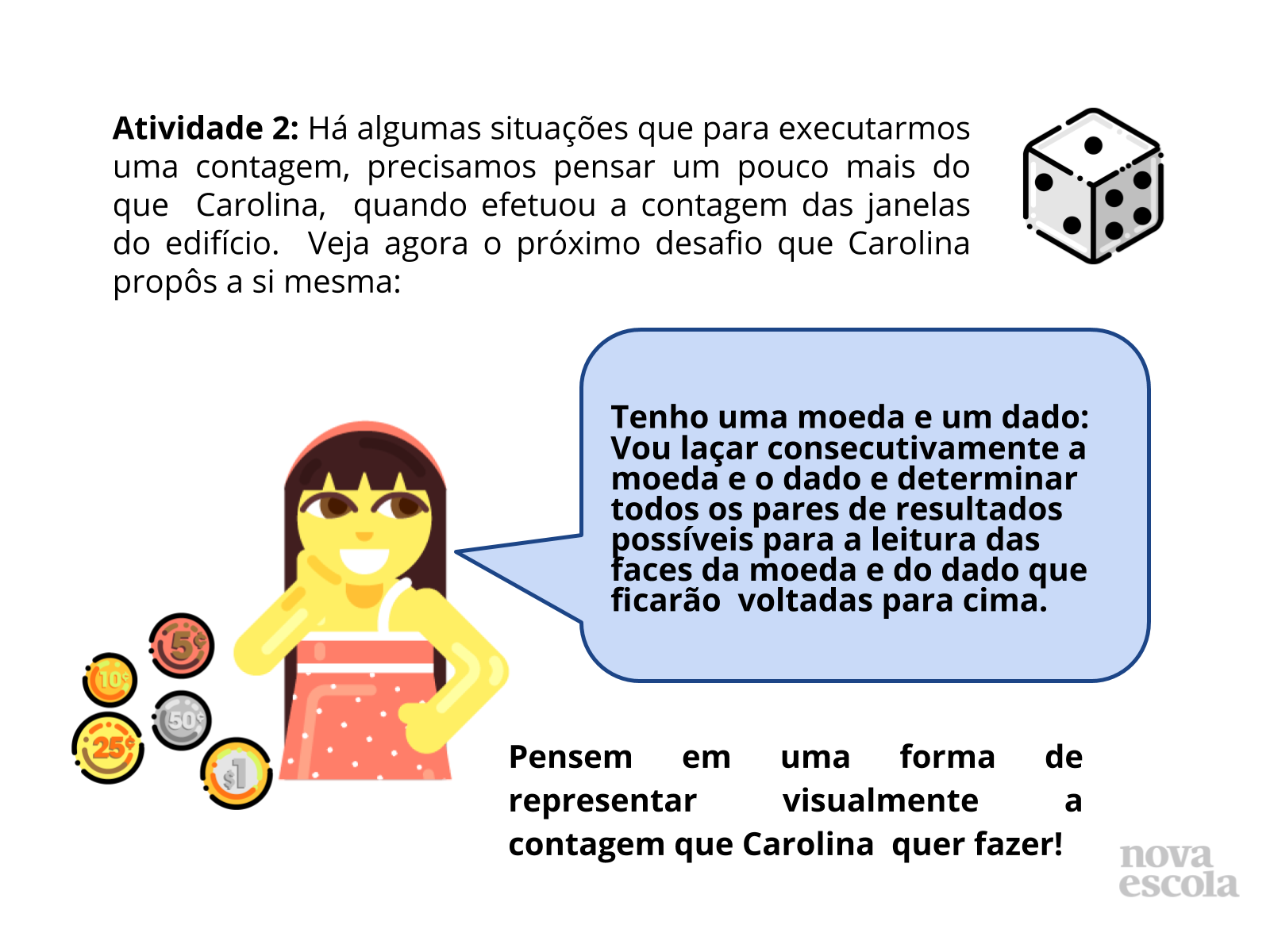
Tempo sugerido: 6 minutos (slides 3 a 7)
Orientação: Organize os alunos em duplas e de forma que não fiquem de costas uns para os outros. Projete o slide 3 e/ou distribua cópias impressas da atividade, leia com a turma e dê tempo para uma discussão sobre a forma com que a personagem irá proceder para determinar o número de janelas da fachada do prédio. Após ouvir algumas estratégias expostas pelos estudantes. Após esse momento, discuta com a turma o texto do slide 4 e peça para os estudantes exemplificarem outras situações em que podem fazer uma contagem de maneira indireta. Espera-se que eles, neste momento dêem exemplos de situações onde se aplica a “organização retangular” usada neste caso, ou em qualquer outro em que os objetos a serem contados possam ser dispostos em forma de retângulo. Não esqueça que podem surgir exemplos que se apliquem raciocínios muito diferentes destes, devem ser valorizados e discutidos, mas validados ou refutados com cautela, no decorrer da aula, quando surgirem oportunidades adequadas. Se for possível projete o slide 6 ou represente na lousa para que os estudantes vejam uma possibilidade para o diagrama de árvore. É possível que os estudantes já tenham percebido que para o total de possibilidades, basta multiplicar as opções de faces da moeda pelas opções de faces do dado, você pode até validar isso, mas chame atenção para o fato de não estarmos querendo apenas quantas possibilidades também queremos determinar quais são elas.
Propósito: Apresentar o enunciado da atividade e propor uma reflexão sobre métodos indiretos de contagem preparando o estudante para a resolução da atividade principal.
Discuta com a turma:
- É importante buscarmos métodos mais eficientes de realizar contagens por questões de praticidade pois, as vezes contar um por um demanda muito tempo e até mesmo erros na própria contagem?
- O que é um par ordenado?
Sugestão de resposta: par ordenado (x,y) é um par de elementos de conjuntos onde ordem de ocorrência desses elementos é relevante. Neste caso, x é o primeiro elemento e y é o segundo elemento.
- Pergunte por que, multiplicando 2 por 6 podemos obter a quantidade total de pares ordenados diferentes que se podem formar.
Sugestão de resposta: Para cada face da moeda que são 2, dispomos de 6 possibilidades para a face do dado. Portanto, Carolina tem 12 ( duas vezes seis) possibilidades para seus resultados.
- Qual a diferença entre perguntar quais e quantas possibilidades?
Sugestão de resposta: Quando a na pergunta aparece “quantas”, um número basta para responder a pergunta. Porém quando aparece “quais” é preciso representar uma a uma as possibilidades possíveis.
Aquecimento
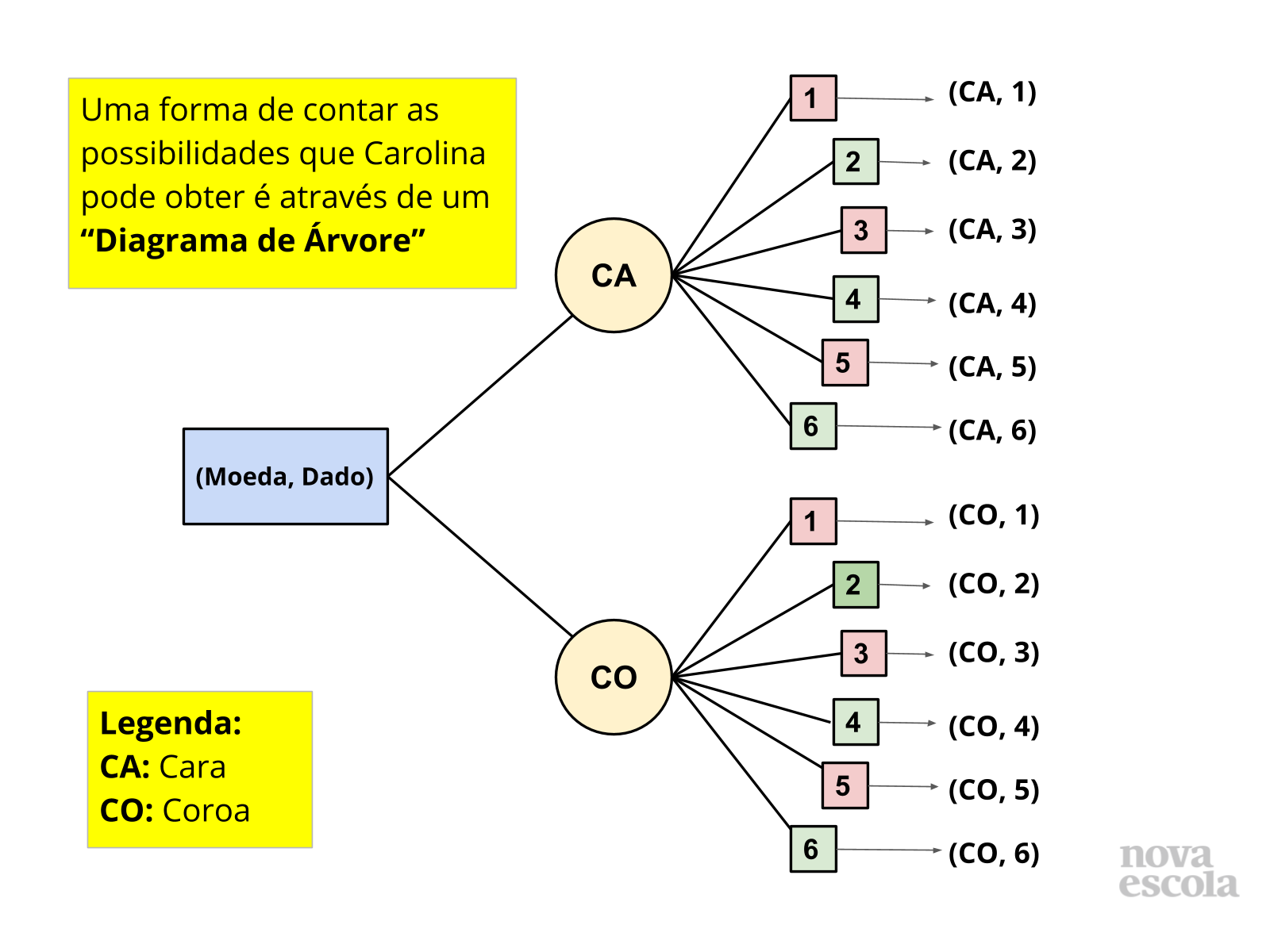
Tempo sugerido: 6 minutos (slides 3 a 7)
Orientação: Organize os alunos em duplas e de forma que não fiquem de costas uns para os outros. Projete o slide 3 e/ou distribua cópias impressas da atividade, leia com a turma e dê tempo para uma discussão sobre a forma com que a personagem irá proceder para determinar o número de janelas da fachada do prédio. Após ouvir algumas estratégias expostas pelos estudantes. Após esse momento, discuta com a turma o texto do slide 4 e peça para os estudantes exemplificarem outras situações em que podem fazer uma contagem de maneira indireta. Espera-se que eles, neste momento dêem exemplos de situações onde se aplica a “organização retangular” usada neste caso, ou em qualquer outro em que os objetos a serem contados possam ser dispostos em forma de retângulo. Não esqueça que podem surgir exemplos que se apliquem raciocínios muito diferentes destes, devem ser valorizados e discutidos, mas validados ou refutados com cautela, no decorrer da aula, quando surgirem oportunidades adequadas. Se for possível projete o slide 6 ou represente na lousa para que os estudantes vejam uma possibilidade para o diagrama de árvore. É possível que os estudantes já tenham percebido que para o total de possibilidades, basta multiplicar as opções de faces da moeda pelas opções de faces do dado, você pode até validar isso, mas chame atenção para o fato de não estarmos querendo apenas quantas possibilidades também queremos determinar quais são elas. Peça que expliquem como se relaciona o diagrama apresentado no slide 7 com a multiplicação que determina o número total de possibilidades.
Propósito: Apresentar o enunciado da atividade e propor uma reflexão sobre métodos indiretos de contagem preparando o estudante para a resolução da atividade principal.
Discuta com a turma:
- É importante buscarmos métodos mais eficientes de realizar contagens por questões de praticidade pois, as vezes contar um por um demanda muito tempo e até mesmo erros na própria contagem?
- O que é um par ordenado?
Sugestão de resposta: par ordenado (x,y) é um par de elementos de conjuntos onde ordem de ocorrência desses elementos é relevante. Neste caso, x é o primeiro elemento e y é o segundo elemento.
- Pergunte por que, multiplicando 2 por 6 podemos obter a quantidade total de pares ordenados diferentes que se podem formar.
Sugestão de resposta: Para cada face da moeda que são 2, dispomos de 6 possibilidades para a face do dado. Portanto, Carolina tem 12 ( duas vezes seis) possibilidades para seus resultados.
- Qual a diferença entre perguntar quais e quantas possibilidades?
Sugestão de resposta: Quando a na pergunta aparece “quantas”, um número basta para responder a pergunta. Porém quando aparece “quais” é preciso representar uma a uma as possibilidades possíveis.
Aquecimento

Tempo sugerido: 6 minutos (slides 3 a 7)
Orientação: Organize os alunos em duplas e de forma que não fiquem de costas uns para os outros. Projete o slide 3 e/ou distribua cópias impressas da atividade, leia com a turma e dê tempo para uma discussão sobre a forma com que a personagem irá proceder para determinar o número de janelas da fachada do prédio. Após ouvir algumas estratégias expostas pelos estudantes. Após esse momento, discuta com a turma o texto do slide 4 e peça para os estudantes exemplificarem outras situações em que podem fazer uma contagem de maneira indireta. Espera-se que eles, neste momento dêem exemplos de situações onde se aplica a “organização retangular” usada neste caso, ou em qualquer outro em que os objetos a serem contados possam ser dispostos em forma de retângulo. Não esqueça que podem surgir exemplos que se apliquem raciocínios muito diferentes destes, devem ser valorizados e discutidos, mas validados ou refutados com cautela, no decorrer da aula, quando surgirem oportunidades adequadas. Se for possível projete o slide 6 ou represente na lousa para que os estudantes vejam uma possibilidade para o diagrama de árvore. É possível que os estudantes já tenham percebido que para o total de possibilidades, basta multiplicar as opções de faces da moeda pelas opções de faces do dado, você pode até validar isso, mas chame atenção para o fato de não estarmos querendo apenas quantas possibilidades também queremos determinar quais são elas.
Propósito: Apresentar o enunciado da atividade e propor uma reflexão sobre métodos indiretos de contagem preparando o estudante para a resolução da atividade principal.
Discuta com a turma:
- É importante buscarmos métodos mais eficientes de realizar contagens por questões de praticidade pois, as vezes contar um por um demanda muito tempo e até mesmo erros na própria contagem?
- O que é um par ordenado?
Sugestão de resposta: par ordenado (x,y) é um par de elementos de conjuntos onde ordem de ocorrência desses elementos é relevante. Neste caso, x é o primeiro elemento e y é o segundo elemento.
- Pergunte por que, multiplicando 2 por 6 podemos obter a quantidade total de pares ordenados diferentes que se podem formar.
Sugestão de resposta: Para cada face da moeda que são 2, dispomos de 6 possibilidades para a face do dado. Portanto, Carolina tem 12 ( duas vezes seis) possibilidades para seus resultados.
- Qual a diferença entre perguntar quais e quantas possibilidades?
Sugestão de resposta: Quando a na pergunta aparece “quantas”, um número basta para responder a pergunta. Porém quando aparece “quais” é preciso representar uma a uma as possibilidades possíveis.
Atividade Principal

Tempo sugerido: 15 minutos (slides 8 e 9)
Orientações: Projete o slide e/ou entregue uma cópia impressa da atividade, leia uma vez o enunciado para a turma e verifique se todos entenderam o que deve ser feito. Peça inicialmente, para lerem mais uma vez a atividade 1 em silêncio e tentarem iniciar a resolução sozinhos por 2 minutos sozinhos, após esse tempo, libere-os para discutir e concluir suas soluções com o colega de dupla.
Propósito: Apresentar o enunciado e passar as instruções para a resolução da atividade principal
Discuta com a turma:
- Qual a vantagem de aplicar o Princípio Multiplicativo da Contagem para sabermos de antemão quantas combinações devem ser listadas.
- Pergunte quantos problemas eles vão resolver essa aula, uma vez que irão elaborar um problema, passar esse problema para o colega de dupla resolver e receber o problema feito pelo colega para resolver.
Resposta: 3 problemas.
Materiais complementares para impressão:
Atividade Principal

Tempo sugerido: 15 minutos (slides 8 e 9)
Orientações: Projete o slide e/ou entregue uma cópia impressa da atividade, leia uma vez o enunciado para a turma e verifique se todos entenderam o que deve ser feito. Peça inicialmente, para lerem mais uma vez a atividade 1 em silêncio e tentarem iniciar a resolução sozinhos por 2 minutos sozinhos, após esse tempo, libere-os para discutir e concluir suas soluções com o colega de dupla.
Propósito: Apresentar o enunciado e passar as instruções para a resolução da atividade principal
Discuta com a turma:
- Qual a vantagem de aplicar o Princípio Multiplicativo da Contagem para sabermos de antemão quantas combinações devem ser listadas.
- Pergunte quantos problemas eles vão resolver essa aula, uma vez que irão elaborar um problema, passar esse problema para o colega de dupla resolver e receber o problema feito pelo colega para resolver.
Resposta: 3 problemas.
Discussão das Soluções
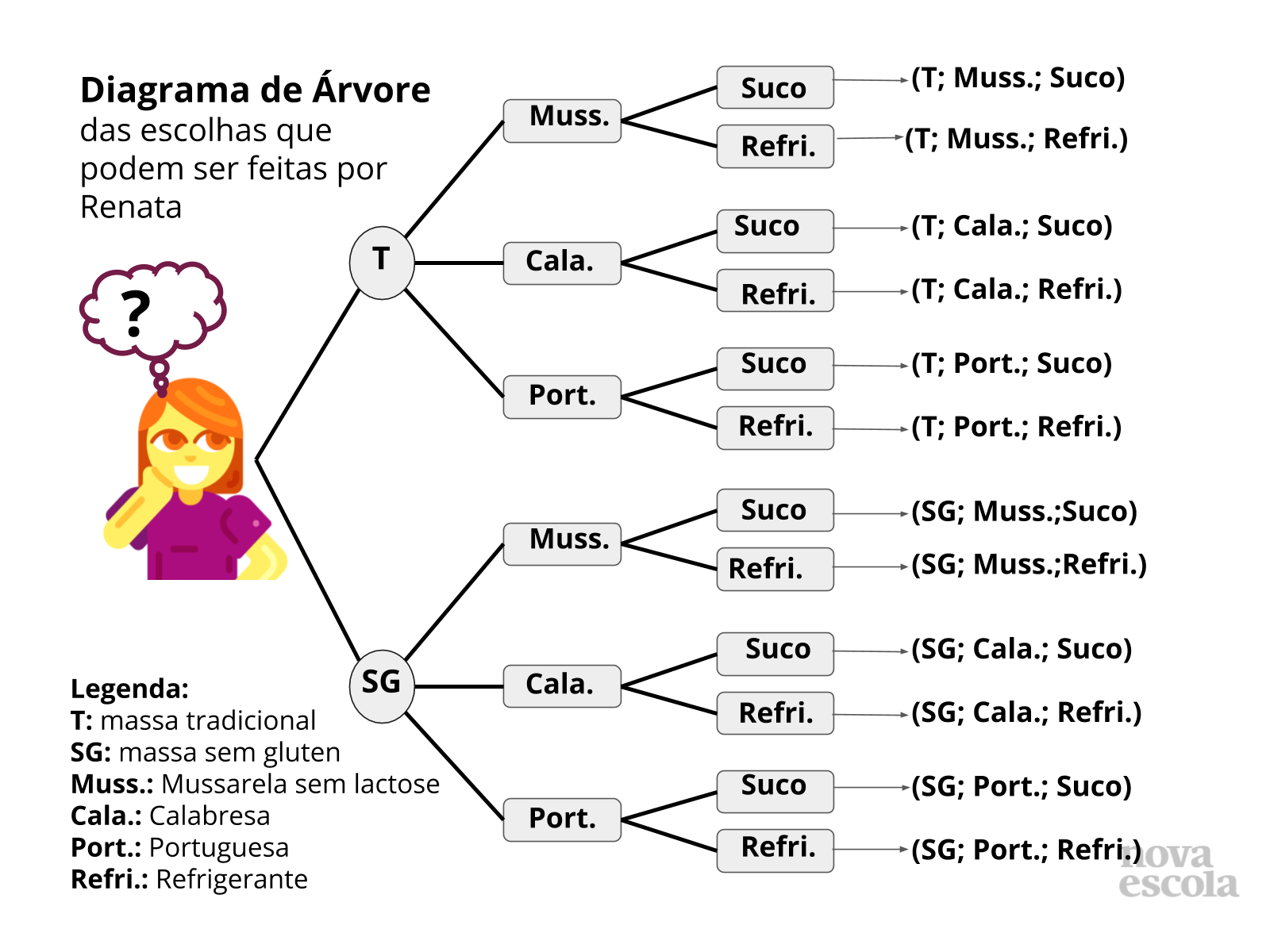
Tempo sugerido: 14 minutos (slides 10 e 11 )
Orientações: Convide os alunos a irem para a lousa apresentar suas soluções, incentive e medie a discussão sobre as diferentes soluções construídas e somente ao final dessa discussão, se julgar necessário, projete o slide com a proposta de solução sugerida no slide 10. A discussão da solução e correção desta atividade deve ser feita de preferência, antes da resolução das atividades 2 e 3. Enfatize os elementos que devem estar presentes no diagrama: Título, que dá ideia clara do que representa e legenda caso haja abreviações ou siglas. Lembre-se que as atividades 2 e 3 são abertas, ali você vai encontrar uma diversidade muito grande de enunciados e soluções. Finalize o momento pedindo para pelo menos um estudante descreva a experiência de ter elaborado um problema de matemática.
Propósito: Apresentar uma solução para a atividade principal
Discuta com a turma:
- Existe alguma outra forma, além do diagrama, para organizar o pensamento e escrever com precisão o conjunto de todas as possibilidades possíveis para a pizza da personagem?
Sugestão de resposta: Também podemos representar todas as possibilidades usando uma tabela de dupla entrada ou diagrama ou pontos em um plano cartesiano, porém nosso objetivo de hoje é construir o diagrama. É possível que, alguns alunos apresentem esse tipo de solução.
- Qual a vantagem de usar o Princípio Multiplicativo para determinarmos de antemão o total de possibilidades antes de construirmos o diagrama?
Sugestão de resposta: Se procedermos assim, saberemos quantas possibilidades o diagrama deve nos fornecer, caso não tenhamos encontrado o valor, devemos analisar o que aconteceu e fazer da forma certa.
Discussão das Soluções

Tempo sugerido: 14 minutos (slides 10 e 11 )
Orientações: Convide os alunos a irem para a lousa apresentar suas soluções, incentive e medie a discussão sobre as diferentes soluções construídas e somente ao final dessa discussão, se julgar necessário, projete o slide com a proposta de solução sugerida no slide 10. A discussão da solução e correção desta atividade deve ser feita de preferência, antes da resolução das atividades 2 e 3. Enfatize os elementos que devem estar presentes no diagrama: Título, que dá ideia clara do que representa e legenda caso haja abreviações ou siglas. Lembre-se que as atividades 2 e 3 são abertas, ali você vai encontrar uma diversidade muito grande de enunciados e soluções. Finalize o momento pedindo para pelo menos um estudante descreva a experiência de ter elaborado um problema de matemática.
Propósito: Apresentar uma solução para a atividade principal
Discuta com a turma:
- Existe alguma outra forma, além do diagrama, para organizar o pensamento e escrever com precisão o conjunto de todas as possibilidades possíveis para a pizza da personagem?
Sugestão de resposta: Também podemos representar todas as possibilidades usando uma tabela de dupla entrada ou diagrama ou pontos em um plano cartesiano, porém nosso objetivo de hoje é construir o diagrama. É possível que, alguns alunos apresentem esse tipo de solução.
- Qual a vantagem de usar o Princípio Multiplicativo para determinarmos de antemão o total de possibilidades antes de construirmos o diagrama?
Sugestão de resposta: Se procedermos assim, saberemos quantas possibilidades o diagrama deve nos fornecer, caso não tenhamos encontrado o valor, devemos analisar o que aconteceu e fazer da forma certa.
Sistematização do conceito
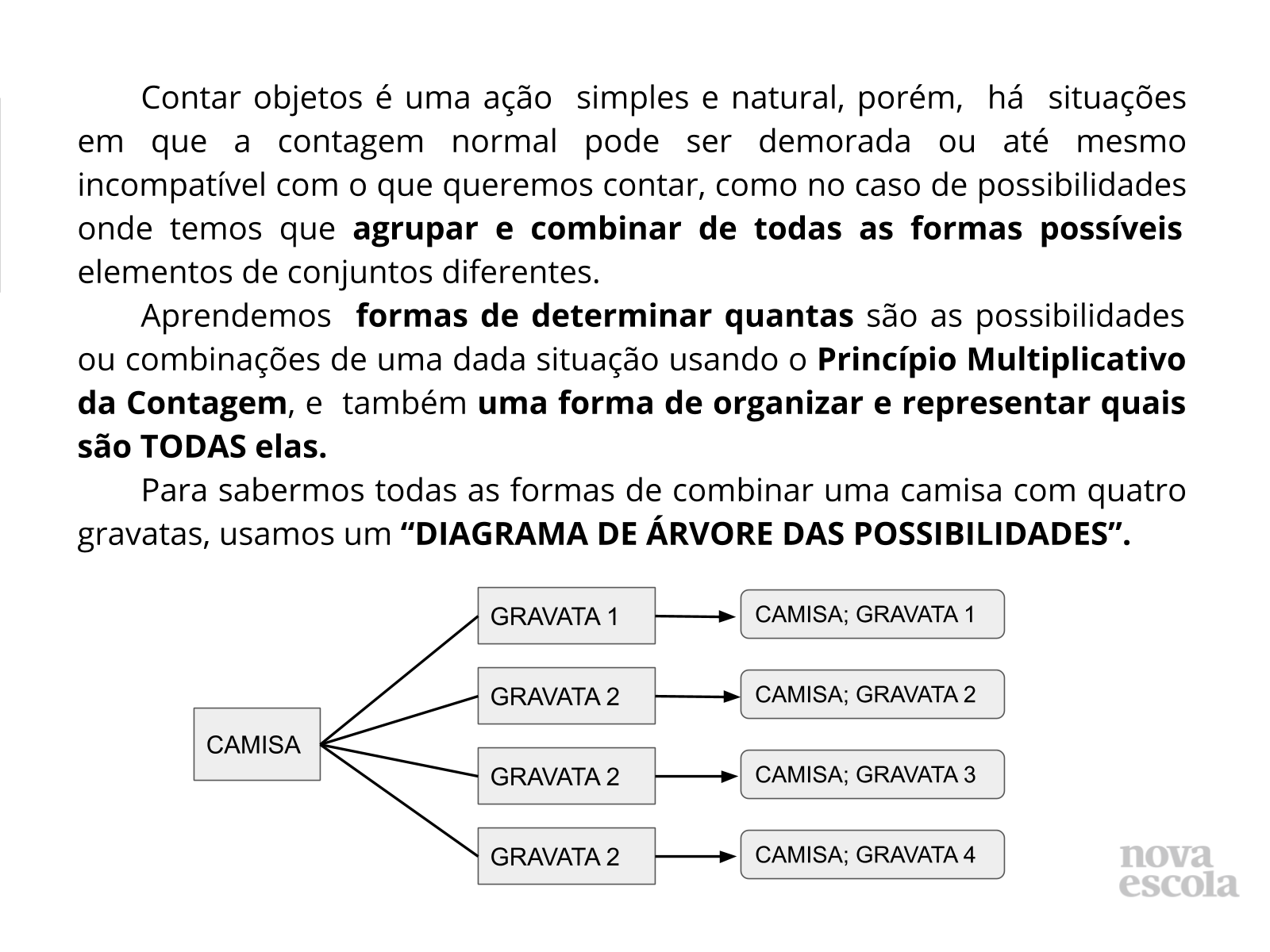
Tempo sugerido: 3 minutos
Orientação: Explique de forma sucinta o texto do slide e tenha em mente, que você deve enfatizar que o diagrama de árvore representa é uma representação para o Princípio Multiplicativo da Contagem que possibilita determinar quantos são os agrupamentos em uma dada situação de contagem porém, se nos for exigido listar quais são todos estes agrupamentos, uma forma prática de organizar a elaboração desta lista é construindo um diagrama de árvore.
Propósito: Sistematizar o conceito de diagrama de possibilidades bem como mostrar a praticidade de seu uso em certas situações de contagem de possibilidades ou combinações.
Discuta com a turma:
- A praticidade de construirmos um diagrama que determine quais são todas as placas de automóveis do país no sistema de 3 letras e quatro algarismos. ( A frota estimada apenas de automóveis no país é de 51 296 981, segundo dados do IBGE: Ministério das Cidades, Departamento Nacional de Trânsito - DENATRAN - 2016. Disponível em http://cod.ibge.gov.br/2vsy7 , acessado em 16/01/2018).
Sugestão de Resposta: Não é prático, manualmente, uma pessoa levaria muito tempo para listar manualmente todas estas placas, mas podemos calcular o número de de todas as placas que podem ser feitas, em instantes, usando o Princípio Multiplicativo e uma calculadora.
Encerramento

Tempo sugerido: 3 minutos
Orientação: Explique para a turma o texto do slide e certifique-se se ainda há dúvidas esclareça-as, pois o próximo momento da aula é a AVALIAÇÃO. Peça que de forma breve eles reflitam e respondam a questão reflexiva do item “Discuta com a turma”. Caso perceba que não há tempo, mande esta questão como tarefa porém, não esqueça de discutir as respostas dos estudantes na aula seguinte. Lembre-se que estamos trabalhando com uma concepção de ensino onde o estudante é o protagonista do processo, então é importante que ele consiga criar significados para o que está aprendendo.
Propósito: Apresentar um resumo do tema trabalhado na aula e enunciar o Princípio Multiplicativo da Contagem.
Discuta com a turma:
- Diferencie para os estudantes escolhas independentes e não independentes:
Sugestão de explicação: A escolha entre 3 pares de tênis e 2 pares de sapatos não são independentes pois ou usamos tênis ou usamos sapato. Em um caso como este não podemos multiplicar as opções para tênis pelas opções para sapatos, pois estaremos considerando combinações em que a pessoa estará usando em um pé um tênis e no outro um sapato. Neste tipo de situação as escolhas não são independentes uma da outra. Dizemos que elas são exclusivas, a escolha de uma, impossibilita a escolha da outra.
- Questão reflexiva: O que você aprendeu na aula de hoje que ainda não sabia? Como você pensa que pode aplicar o conceito estudado na aula de hoje em sua vida fora da escola?
Atividade de Raio X

Tempo sugerido: 5 min para a resolução e 2 minutos para correção.
Orientação: Ler junto com os alunos, verificar se todos compreenderam o problema e sabem o que devem fazer, e pedir para que resolvam. Circule pela sala para verificar as resoluções. Lembre-se que neste momento você está avaliando os avanços dos estudantes em relação ao conteúdo da aula. Procure identificar as dúvidas que ainda ficaram e reserve os minutos finais da aula para uma breve correção desta atividade (resolução da atividade disponível para impressão).
Propósito: Verificar a assimilação dos conteúdos desenvolvidos durante a aula.
Discuta com a turma:
- Corrigir a atividade na lousa de forma breve usando os três minutos finais da aula.
Materiais complementares para impressão:
Sugestão de adaptação para ensino remoto
Professor, revisite todos os arquivos do plano que você vai orientar e identifique os pontos principais para o trabalho remoto. Lembre-se que as sugestões precisam envolver tanto o uso da tecnologia quanto situações em que a tecnologia não está disponível.
Recursos
USAR APENAS FERRAMENTAS EM PORTUGUÊS E GRATUITAS.
- Necessários: papel e lápis.
- Opcionais: Meet, Hangout, Whatsapp, plataforma da Khan Academy (disponível aqui).
Para este plano, foque na etapa ATIVIDADE PRINCIPAL.
Aquecimento
O aquecimento serve aqui como um exemplo para o uso de árvore de possibilidades ou diagrama de árvore. Ele pode ser suprimido para manter o foco na ATIVIDADE PRINCIPAL. Caso sua turma nunca tenha tido conhecimento do uso de árvore de possibilidades nos problemas de contagem, sugerimos manter a aula centrada no Aquecimento.
Atividade principal
Embora a aula esteja centralizada no uso de árvore de possibilidades, os alunos podem resolver usando outras estratégias. Sugerimos manter a liberdade de escolha para resolução da situação. Nas discussões das soluções você pode propor a árvore como uma forma de resolução. Há uma etapa de elaboração de problemas de contagem. Você pode solicitar que os alunos elaborem e encaminhem via Whatsapp. Você pode fazer uma seleção dos problemas para que todos os alunos resolvam.
Na plataforma da Khan Academy, há vários vídeos e atividades sobre o tema. Essa pode ser uma proposta interessante para os alunos que têm acesso à Internet. Os vídeos a seguir são introdutórios para os problemas de combinação:
Vídeo 1 (disponível aqui).
Vídeo 2 (disponível aqui).
Vídeo 3(disponível aqui).
Discussão das soluções
É interessante disponibilizar aos alunos estratégias diferentes de resolução focando na árvore de possibilidades. Você pode disponibilizar para todos alguns problemas selecionados que eles elaboraram na etapa 2 da Atividade principal.
O Whatsapp pode ser usado para intermediar essa mediação. Se houver recursos tecnológicos para discussão em tempo real com a turma, utilize-os para esclarecer dúvidas e sugerir propostas que ampliem e consolidem as amprendizagens. Sugestão de recursos on line para discussões: Meet ou Hangout (Google).
Sistematização
xxxx
Encerramento
Use a definição do Princípio Multiplicativo de contagem nas discussões das soluções.
Raio X
O Raio X pode ser usado como forma de revisão das aprendizagens, assim como as atividades complementares.
Convite às famílias
Os problemas de contagem podem funcionar como um jogo, um desafio. Podem ser propostos para as famílias discutirem como se resolveria o Raio X. Lembre-se que pessoas não letradas são capazes de realizar alguns problemas de contagem.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Altamiro Marlon Ribeiro
Mentor: Amanda Ferreira Verardo Bilia
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
(EF08MA03): Princípio multiplicativo da contagem (resolução de problemas de contagem)
Conhecimento prévios:
Noção de organização triangular e construção de grafos e tabelas para representação de contagens.
Objetivos específicos
Elaborar e resolver problemas de contagem relacionando o Princípio Multiplicativo da Contagem com do Diagrama de árvore.
Conceito-chave
Contagem, princípio multiplicativo, diagrama de árvore
Recursos necessários
- Projetor (caso haja)
- Atividades impressas em folhas, coladas no caderno ou não.
- Folhas A4
- Lápis de cor e régua











