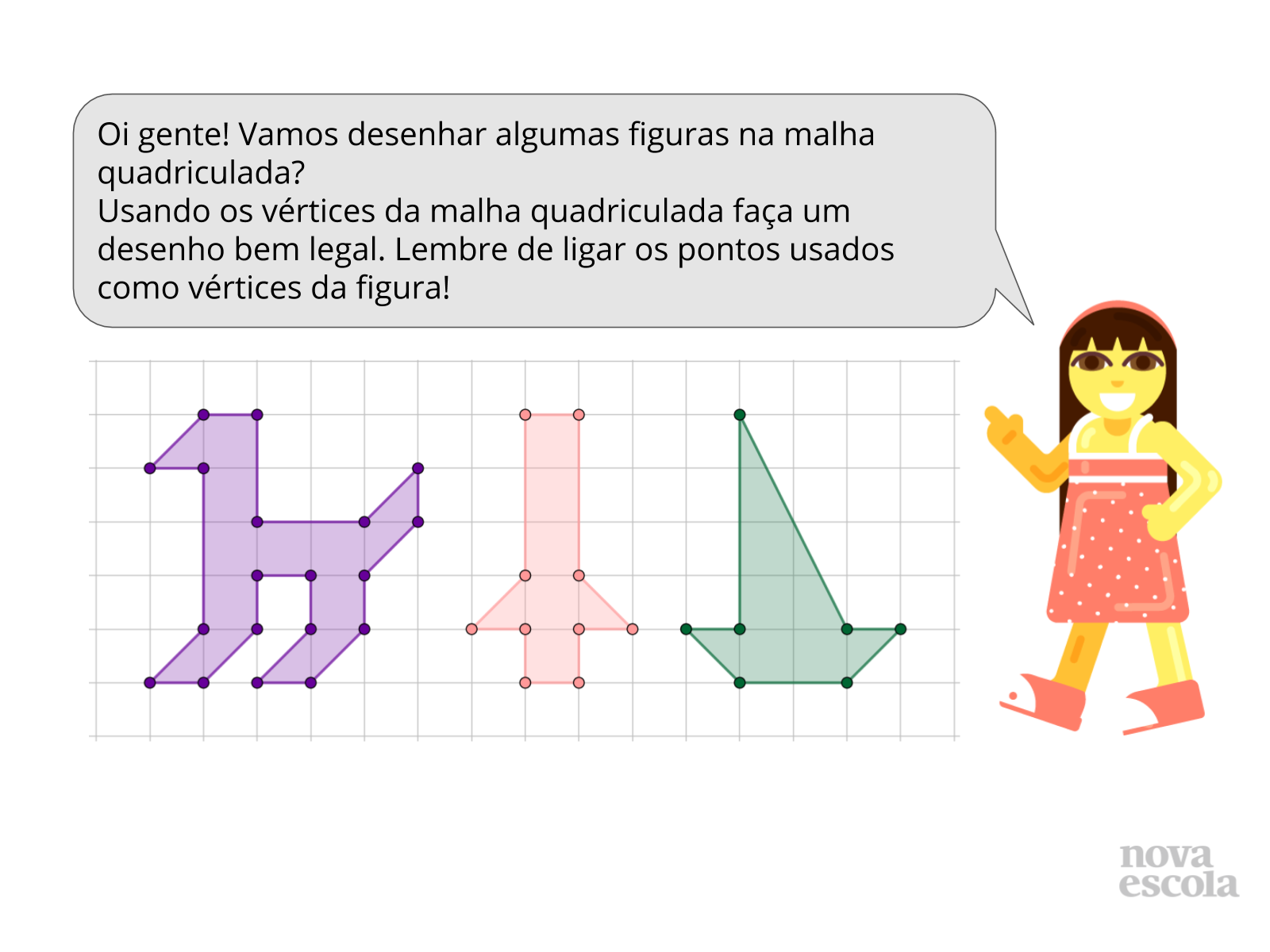
Atividade principal
Plano de Aula
Plano de aula: Recortando e Moldando o Teorema de Pitágoras
Plano 8 de uma sequência de 11 planos. Veja todos os planos sobre Teorema de Pitágoras e suas aplicações
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Sebastiao Rodrigues da Silva
Mentor: Lara Martins Barbosa
Especialista de área: Pricilla Mendes Cerqueira
Habilidade da BNCC
(EF09MA14) Resolver e elaborar problemas de aplicação do teorema de Pitágoras ou das relações de proporcionalidade envolvendo retas paralelas cortadas por secantes.
Objetivos específicos
Deduzir o Teorema de Pitágoras através de recortes e atividades práticas.
Conceito-chave
Utilização de recortes em folhas de papel cartão ou EVA como forma de auxiliar na dedução e compreensão do Teorema de Pitágoras.
Recursos necessários
- Uma folha de papel cartão ou EVA
- Régua
- Lápis comum
- Lápis de cor ou pincel hidrocor
- Tesoura
- Atividades impressas
Conhecimentos prévios:
- Triângulos Retângulos
- Ângulos complementares e suplementares
- Congruência de triângulos
- Área de quadrado e triângulo
Habilidades BNCC:
Objetivos de aprendizagem
Deduzir o Teorema de Pitágoras através de recortes e atividades práticas.
Resumo da Aula
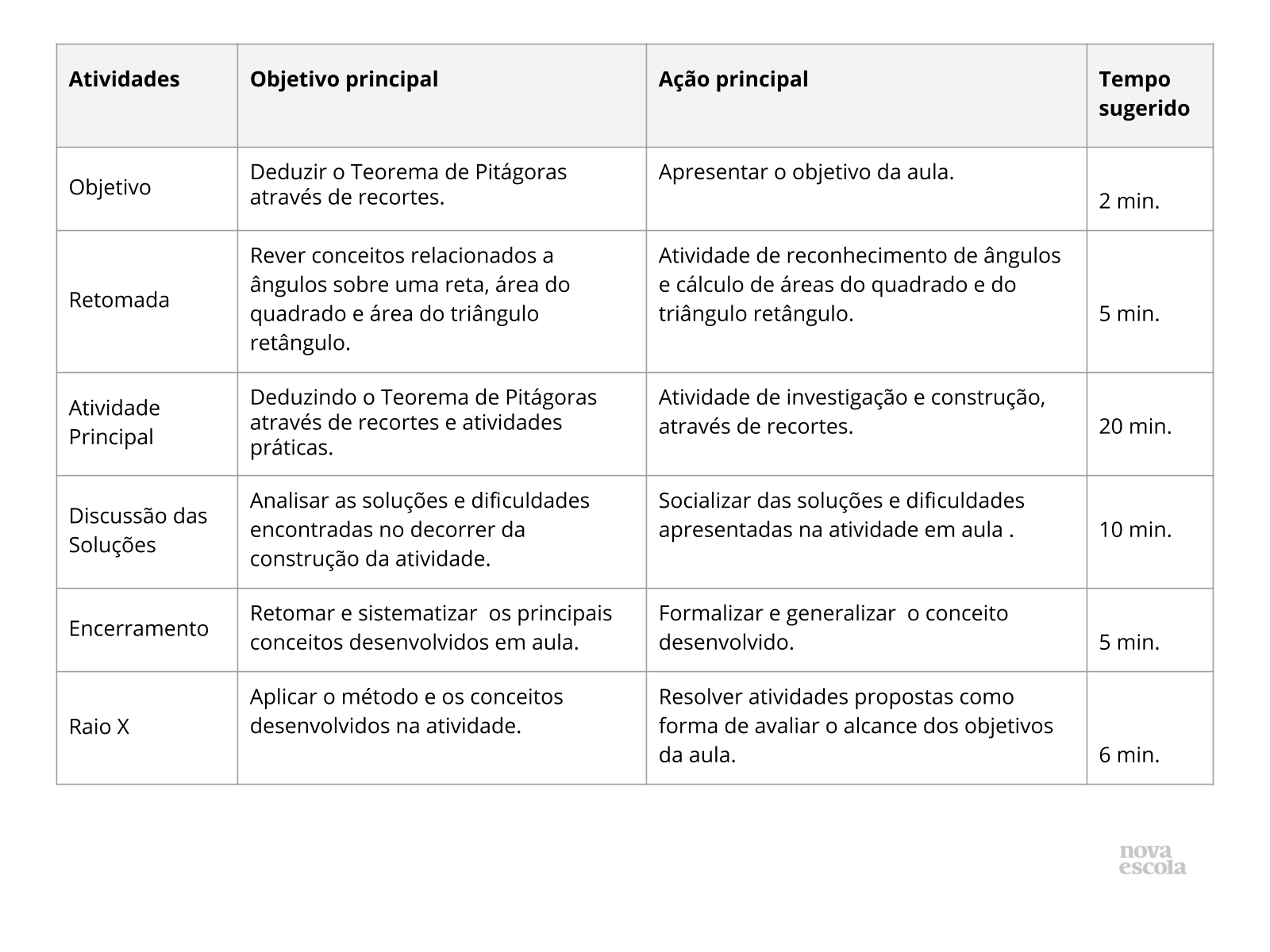 Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientações:
Apresente o objetivo da aula de forma clara, de modo que os alunos percebam o que se deseja alcançar com as atividades a serem desenvolvidas na aula. Poderá usar um esquadro de madeira para mostrar os elementos que compõe um triângulo retângulo, destacando a relação entre as medidas dos lados expressas pelo teorema de Pitágoras.
Propósito: Apresentar o objetivo da aula.
Discuta com a turma:
- Como se chama cada lado do triângulo retângulo?
- O que nos diz o Teorema de Pitágoras?
Aquecimento
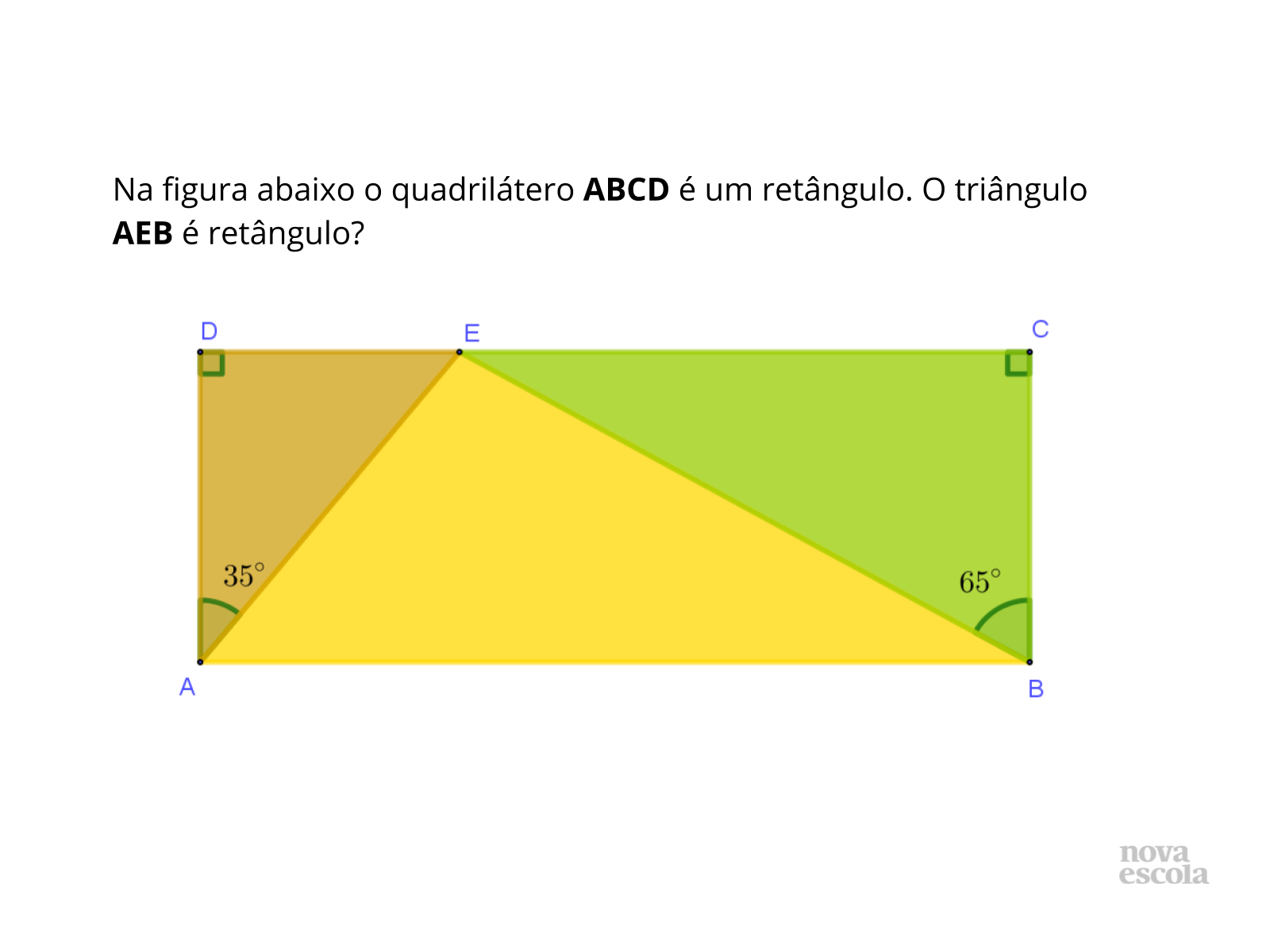
Tempo sugerido: 5 minutos. (slides 3 e 4) .
Orientações:
Realize a atividade em duplas. Disponibilize a atividade impressa para cada dupla.
Propósito: Rever conceitos relacionados a ângulos sobre uma reta e ângulos no triângulo retângulo.
Discuta com a turma:
- Qual a medida do ângulo entre 3 pontos sobre uma reta?
- Quanto vale a soma dos ângulos internos de um triângulo?
- No triângulo retângulo, quanto mede o maior ângulo?
- Quando dois ângulos são complementares?
- Materiais complementares:
Retomada
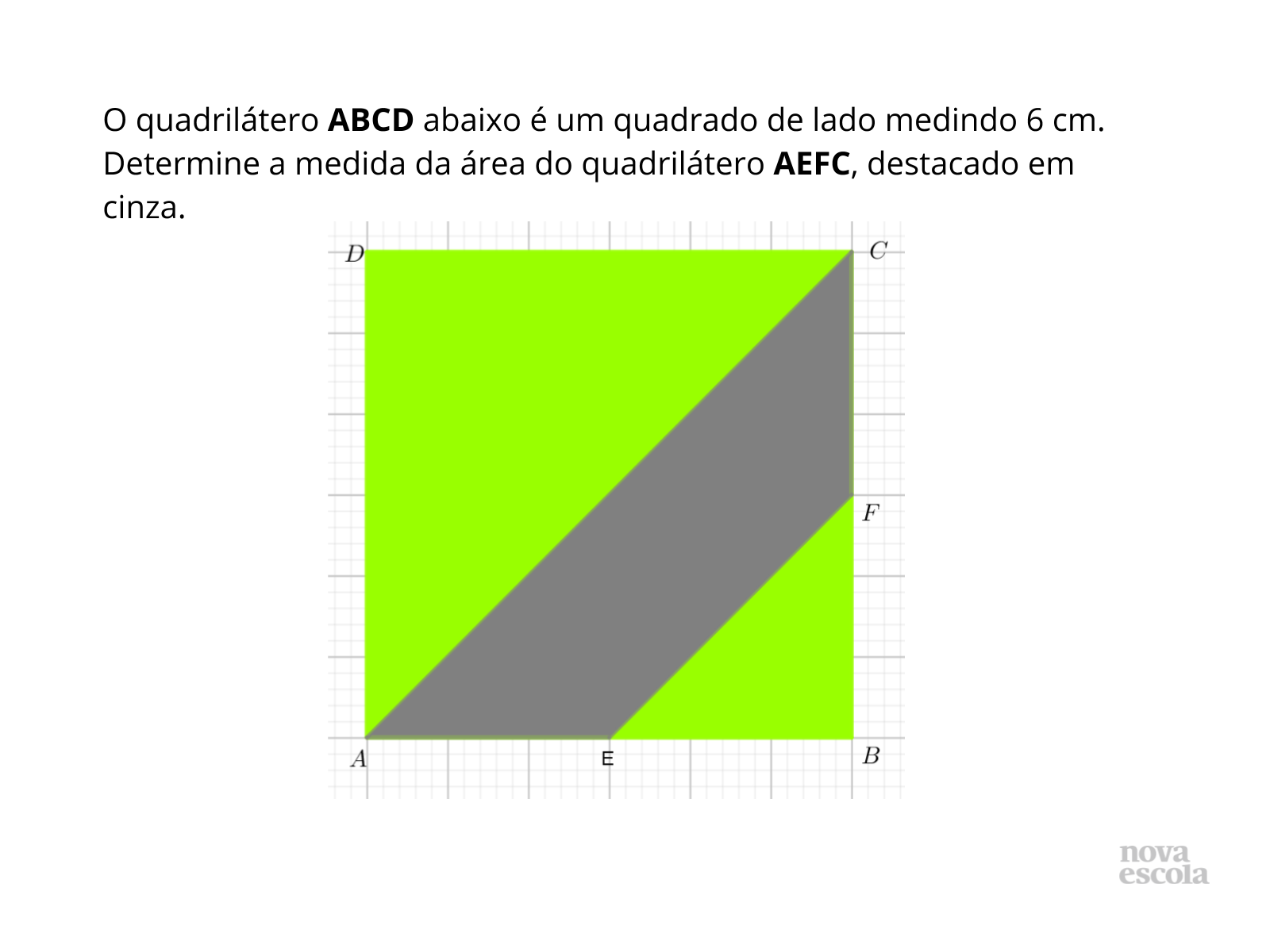
Tempo sugerido: 5 minutos (slides 3 e 4) .
Orientações:
Realize a atividade em duplas. Disponibilize a atividade impressa para cada dupla.
Propósito: Rever conceitos relacionados ao cálculo de áreas do quadrado, do triângulo retângulo e a noção de composição de áreas.
Discuta com a turma:
- Quando um quadrilátero é um quadrado?
- Como se determina a área de um quadrado? E de um triângulo retângulo?
Atividade Principal

Tempo sugerido: 20 minutos. (slides 5, 6, 7, 8).
Orientações:
Material necessário para a construção: Papel cartão ou EVA, régua, lápis comum, lápis de cor ou pincel hidrocor, tesoura. Disponibilize essa quantidade de material por equipe. Realize a atividade em equipes de no máximo 3 componentes, para que possam interagir e trocar ideias em torno da construção e dessa forma construírem uma hipótese coletiva. Estimule as equipes a construírem quadrados com tamanhos diferentes. Disponibilize a imagem impressa ou a projete para os alunos, assim poderão visualizar antecipadamente o que se pretende construir, tendo mais tempo para realizar as investigações em torno dos questionamentos e construírem uma conjectura para a demonstração algébrica. Oriente os alunos a escreverem internamente as letras a, b e c, que representam medidas genéricas, para que após os recortes as mesmas apareçam nas figuras.
Propósito: Utilizar recortes para deduzir o Teorema de Pitágoras
Discuta com a turma:
- Quais as propriedades fundamentais de um quadrado?
- Quando dois quadrados são congruentes?
- Quando dois triângulos são congruentes?
- Como se denomina as medidas dos lados de um triângulo retângulo?
- Materiais complementares:
Atividade Principal

Tempo sugerido: 20 minutos. (slides 5, 6, 7, 8).
Orientações:
Disponibilize a imagem impressa ou a projete para os alunos.
Propósito: Utilizar recortes para deduzir o Teorema de Pitágoras
Discuta com a turma:
- Quais as propriedades fundamentais de um quadrado?
- Quando dois quadrados são congruentes?
- Quando dois triângulos são congruentes?
- Como se denomina as medidas dos lados de um triângulo retângulo?
Atividade Principal

Tempo sugerido: 20 minutos. (slides 5, 6, 7, 8).
Orientações:
Oriente os alunos sobre a importância dos recortes serem o mais perfeito possível.
Propósito: Utilizar recortes para deduzir o Teorema de Pitágoras
Discuta com a turma:
- Qual a soma dos dois ângulos agudos em um triângulo retângulo?
- De que forma podemos construir um retângulo com dois triângulos retângulos?
- De quantos modos podemos colocar os dois retângulos formados pelo triângulos, dentro do quadrado MNOP, de modo que dois lados não fiquem sobrepostos e tenham em comum um único vértice?
Atividade Principal

Tempo sugerido: 20 minutos. (slides 5, 6, 7, 8).
Orientações:
Os questionamentos investigativos visam nortear os alunos de modo a construírem uma hipótese independente. Assim, trabalhe com as equipes, buscando fazer com que os mesmos alcancem o objetivo da aula de forma independente.
Propósito: Utilizar recortes para deduzir o Teorema de Pitágoras
Discuta com a turma:
- Quais as figuras formadas pelos espaços vazios?
- Qual a soma das áreas das figuras formadas pelos espaços vazios não ocupados pelos retângulos?
- O que vocês percebem? Há alguma relação entre as medidas dos lados de um triângulo retângulo?
Discussão das Soluções
Tempo sugerido: 10 minutos. (slides 9, 10 e 11).
Orientações:
Estimule as equipes a socializarem e discutirem suas dificuldades e soluções.
Propósito: Discutir a solução e as dificuldades apresentadas no decorrer da atividade.
Discuta com a turma:
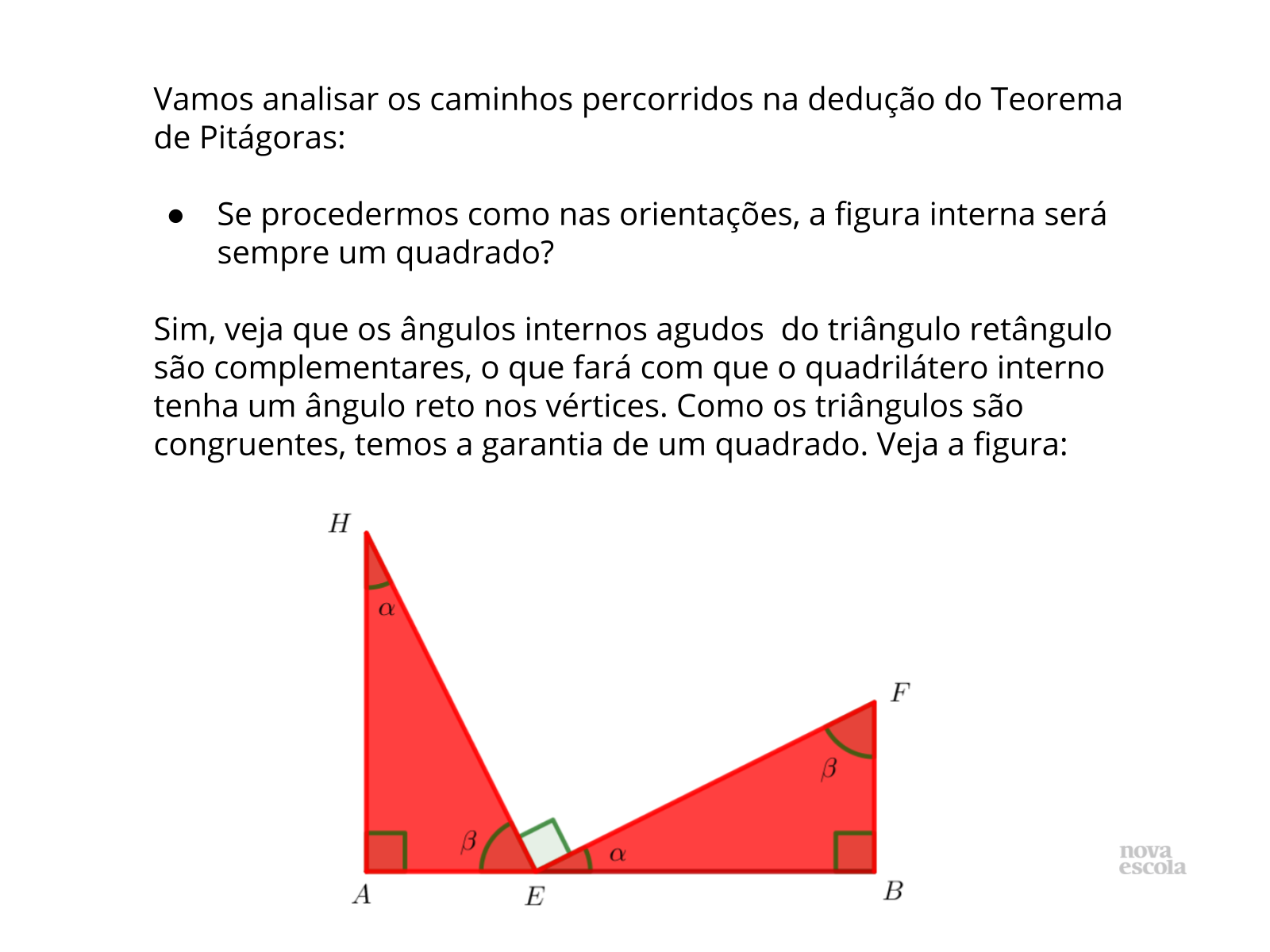
- Por que a soma de dois ângulos agudos de um triângulo retângulo vale 90°?
- Quanto mede cada ângulo do quadrado?
- Além dos ângulos retos, o que se precisa para que um quadrilátero seja um quadrado?
Discussão das Soluções

Tempo sugerido: 10 minutos. (slides 9, 10 e 11).
Orientações:
Estimule as equipes a socializarem e discutirem suas dificuldades e soluções.
Propósito: Discutir a solução e as dificuldades apresentadas no decorrer da atividade.
Discuta com a turma:
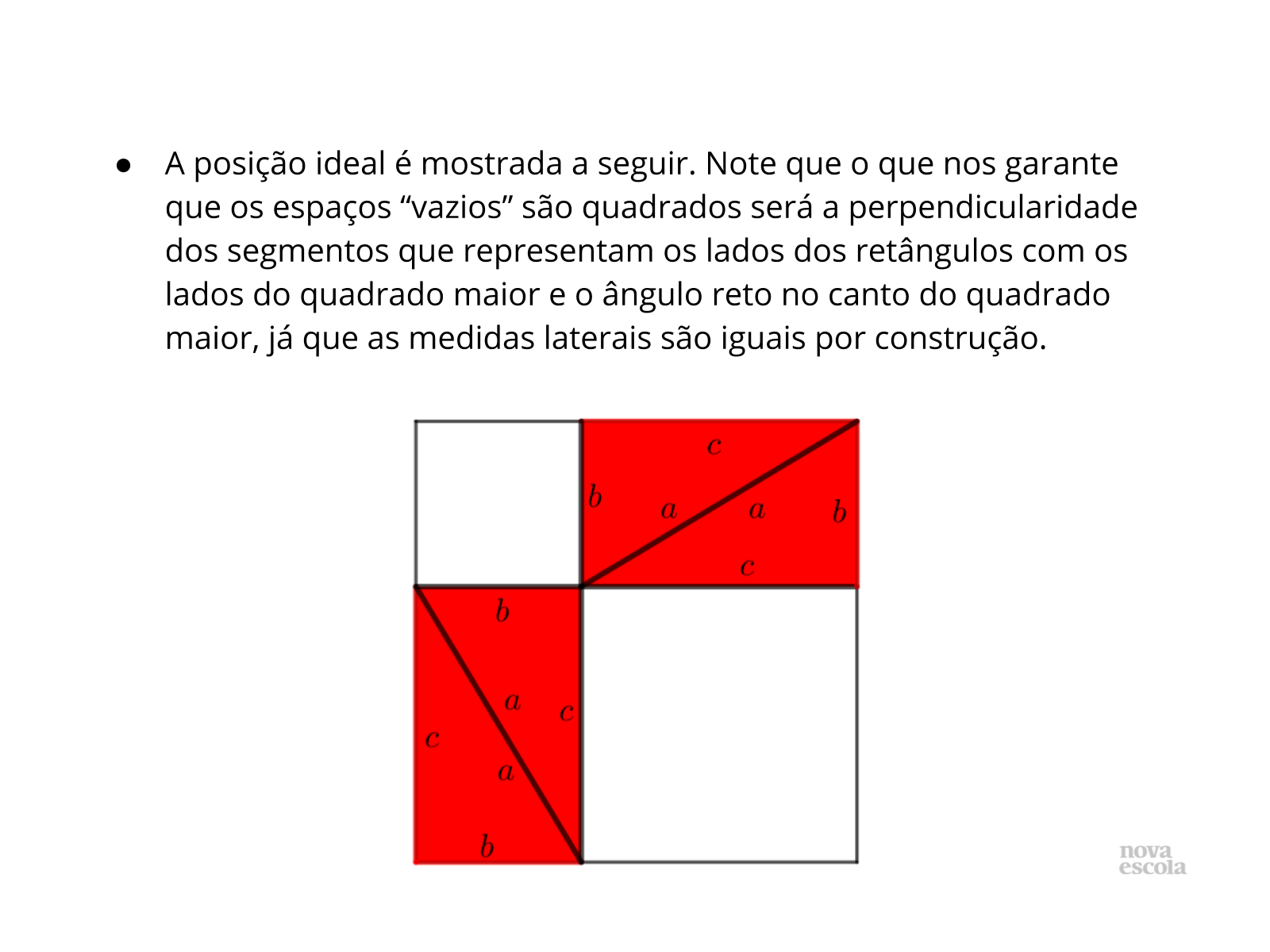
- Vocês podem mostrar alguma outra posição diferente dessa?
Discussão das Soluções
Tempo sugerido: 10 minutos. (slides 9, 10 e 11).
Orientações:
Estimule as equipes a socializarem e discutirem suas dificuldades e soluções.
Propósito: Discutir a solução e as dificuldades apresentadas no decorrer da atividade
Discuta com a turma:
- A diferença nos tamanhos dos quadrados, fez surgir uma relação diferente?
- A conclusão da equipe é a mesma da equipe vizinha?
- O que isso significa?
Encerramento
Tempo sugerido: 5 minutos. (Slides 12 e 13).
Orientações:
Encerre a aula resumindo com os alunos o conceito desenvolvido na aula através dos recortes e construções.
Propósito: Sintetizar o que foi desenvolvido na aula.
Discuta com a turma:
- As diferentes medidas adotadas influenciaram nos resultados?
Encerramento
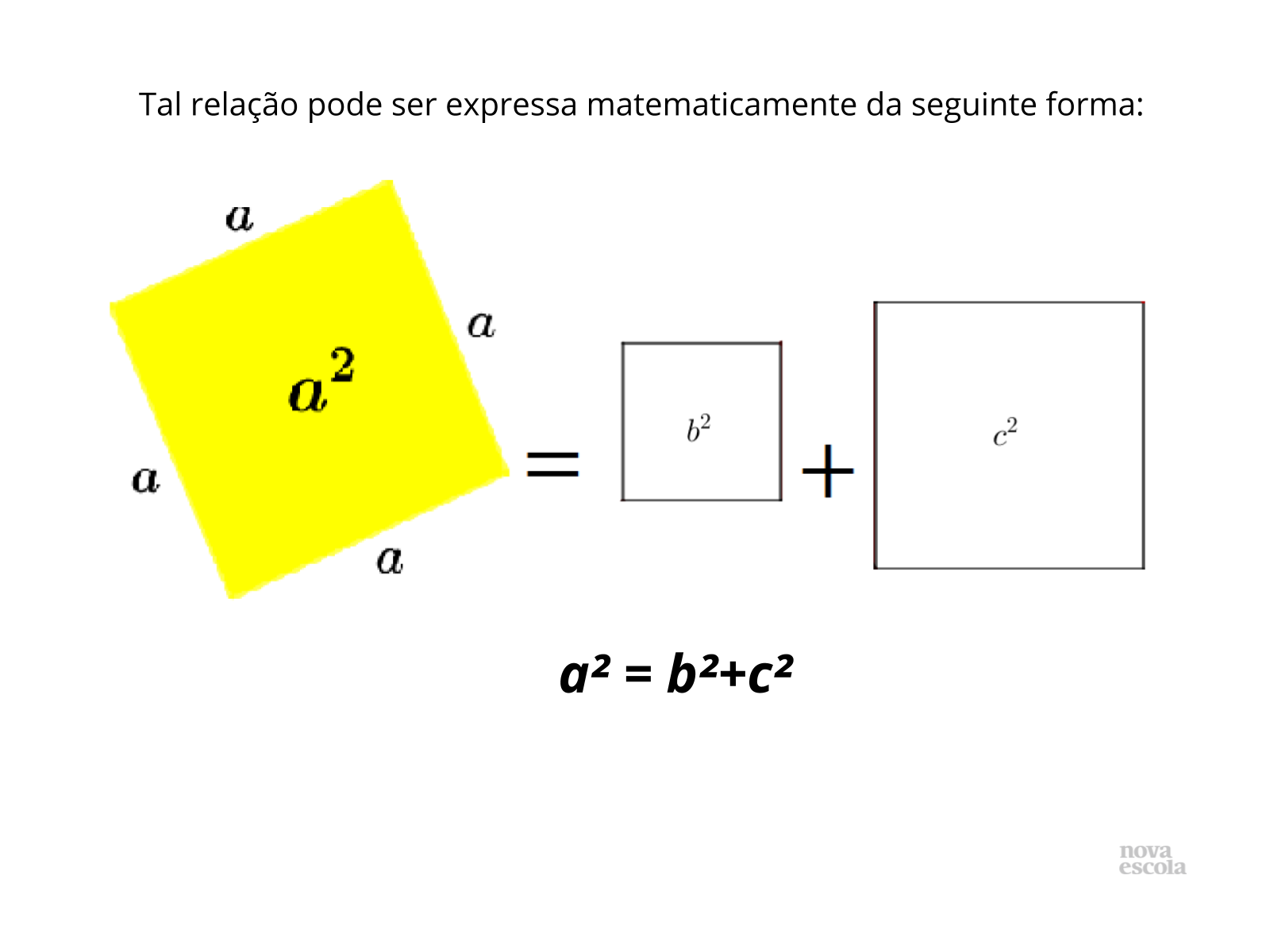
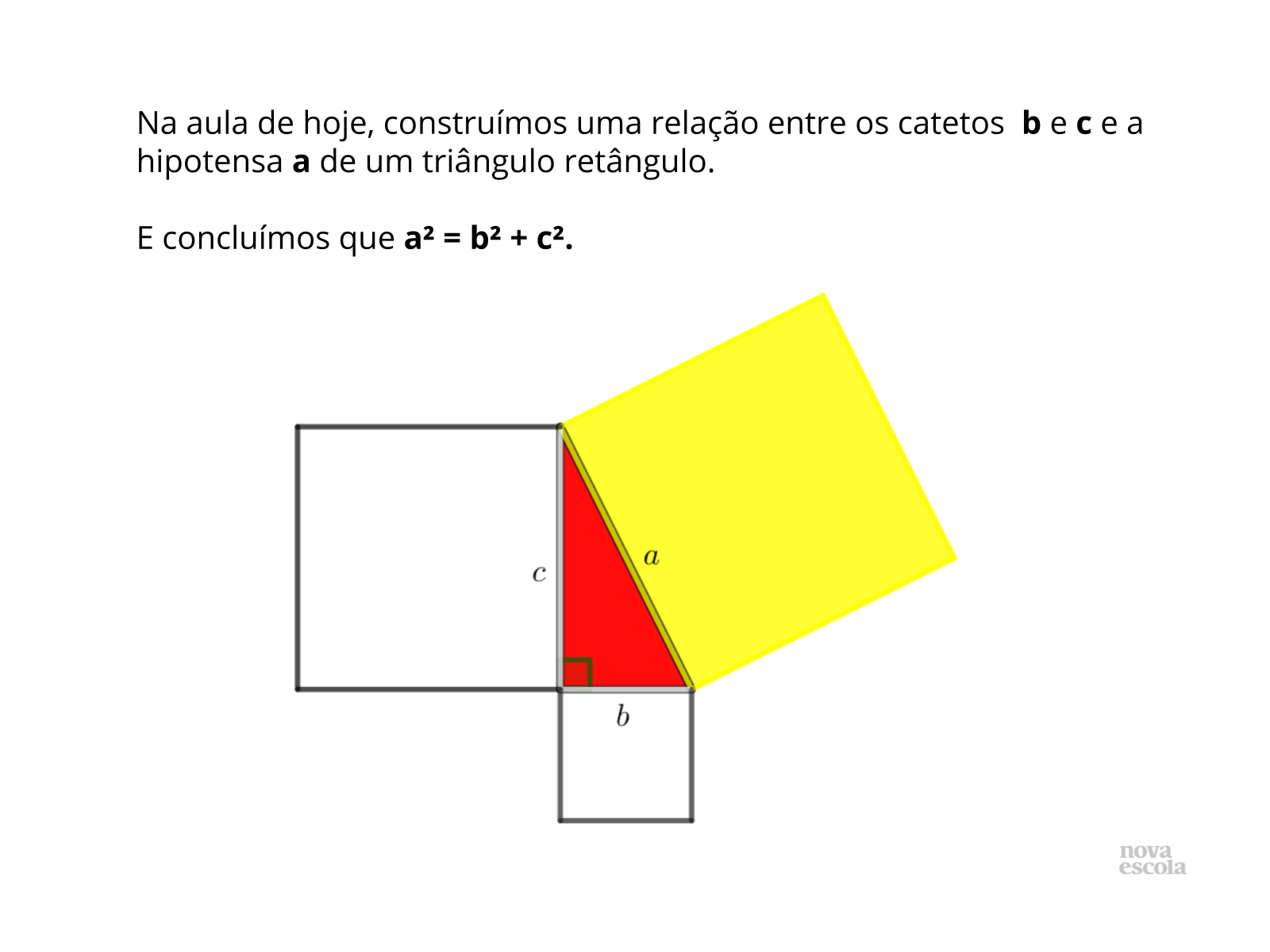
Tempo sugerido: 5 minutos. (Slides 12 e 13).
Orientações: Encerre a aula resumindo com os alunos o conceito desenvolvido na aula através dos recortes e construções.
Propósito: Sintetizar o que foi desenvolvido na aula.
Discuta com a turma:
- Qual o significado da relação obtida?
- Como vocês expressaram tal relação verbalmente?
Raio X

Tempo sugerido: 6 minutos.
Orientações: A atividade deve ser realizada individualmente. O ideal é que os alunos recortem e identifiquem as cinco regiões destacadas, pois através da manipulação concreta torna-se-a mais fácil estabelecer as relações entre as áreas dos quadrados construídos sobre os catetos e o quadrado sobre a hipotenusa.
Propósito: Avaliar se os objetivos da aula foram alcançados.
Materiais complementares:
Resolução atividade complementar/a>
Raio X
Tempo sugerido: 6 minutos.
Orientações:
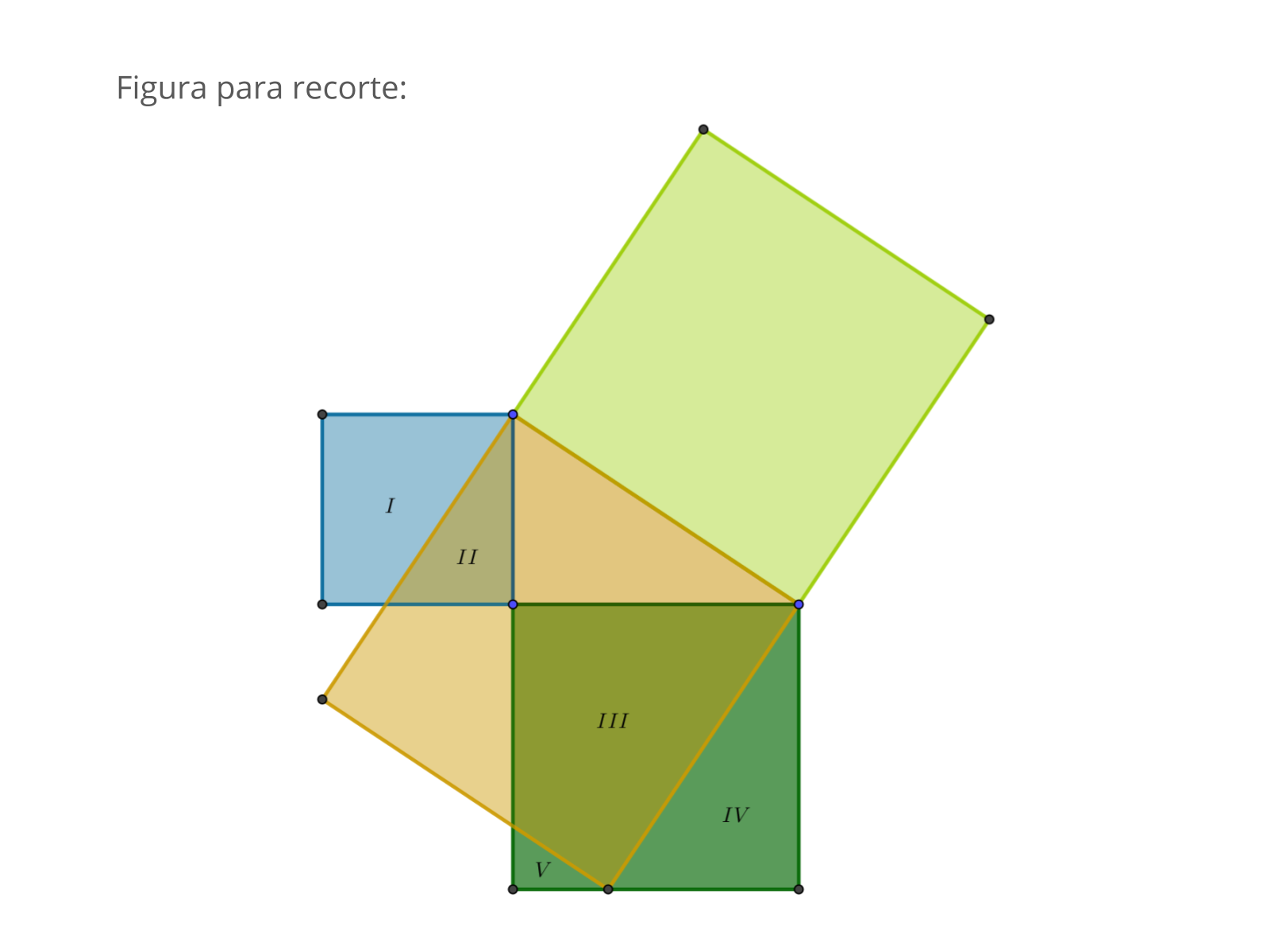
A atividade deve ser realizada individualmente. Disponha a figura impressa para os alunos. O ideal é que os alunos recortem e identifiquem as cinco regiões destacadas, pois através da manipulação concreta torna-se-a mais fácil estabelecer as relações entre as áreas dos quadrados construídos sobre os catetos e o quadrado sobre a hipotenusa. Caso disponha de mais tempo, o professor orientar a construção da figura, da seguinte forma:
- Constrói-se um quadrado sobre cada lado do triângulo;
- O quarto quadrado ( interno à hipotenusa) constrói-se ampliando os dois lados que tem vértices comuns com a hipotenusa, de modo a obter um quadrado congruente ao quadrado construído sobre a hipotenusa
Propósito: Avaliar se os objetivos da aula foram alcançados.
Discussão com a turma:
- Qual a medida da área de cada quadrado?
- Quanto vale a soma das áreas destacadas?
- Qual a relação entre as áreas destacadas e a área do quadrado sobre a hipotenusa?
Raio X

Tempo sugerido: 6 minutos.
Orientações: Peça que recortem e identifiquem as cinco regiões destacadas, pois através da manipulação concreta torna-se-a mais fácil estabelecer as relações entre as áreas dos quadrados construídos sobre os catetos e o quadrado sobre a hipotenusa.
Propósito: Avaliar se os objetivos da aula foram alcançados
Sugestão de adaptação para ensino remoto
Código do plano (MAT9_15GEO08)
Ferramentas sugeridas
- Essenciais: Alguma rede social (Whatsapp, Facebook, etc.) régua e papel para anotações.
- Optativas: Calculadora e tesoura.
Aquecimento
- Pela rede social escolhida, inicie esse contato questionando se lembram das condições existentes na soma dos ângulos internos de triângulos e quadriláteros, e oriente as respostas.
- Ainda nessa etapa, questione se lembram o significado de calcular área de um polígono qualquer. Muitos podem relatar fórmulas, mas sua orientação deve ser no sentido de que área é o cálculo de “quantos quadrados unitários (de lado 1)” cabem na superfície do polígono.
Atividade principal
Para realizar a atividade principal deste plano é possível construir quadrados realizando as dobraduras numa folha retangular, já aprendidas e pode ser revisitada no link: https://www.youtube.com/watch?v=FLk879D4fos.
A partir dessa construção determine que sigam os passos da construção prevista no plano original e mande a imagem, para que comparem e verifiquem se ficou semelhante.
Oriente as manipulações dos recortes e os questionamentos, sempre mostrando as imagens quando necessário e incentive que alguns compartilhem as suas para posterior discussão de soluções.
Discussão das soluções, sistematização e encerramento
- Na discussão das soluções, retorne às imagens e identifique uma melhor disposição para perceberem o teorema de Pitágoras.
- Reforce assim que é mais uma maneira geométrica de mostrar a validade do teorema de Pitágoras.
Convite às famílias
Peça para que seus alunos envolvam seus familiares, próximos neste momento, e relatem suas explorações sobre o link acessado pedindo apoio para as manipulações.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Sebastiao Rodrigues da Silva
Mentor: Lara Martins Barbosa
Especialista de área: Pricilla Mendes Cerqueira
Habilidade da BNCC
(EF09MA14) Resolver e elaborar problemas de aplicação do teorema de Pitágoras ou das relações de proporcionalidade envolvendo retas paralelas cortadas por secantes.
Objetivos específicos
Deduzir o Teorema de Pitágoras através de recortes e atividades práticas.
Conceito-chave
Utilização de recortes em folhas de papel cartão ou EVA como forma de auxiliar na dedução e compreensão do Teorema de Pitágoras.
Recursos necessários
- Uma folha de papel cartão ou EVA
- Régua
- Lápis comum
- Lápis de cor ou pincel hidrocor
- Tesoura
- Atividades impressas
Conhecimentos prévios:
- Triângulos Retângulos
- Ângulos complementares e suplementares
- Congruência de triângulos
- Área de quadrado e triângulo