Atividade principal
Plano de Aula
Plano de aula: Volume e capacidade do cilindro reto
Plano 5 de uma sequência de 10 planos. Veja todos os planos sobre Volumes e Capacidades
Tem interesse no tema "Neurociência, adolescências e engajamento nos Anos Finais"?
Inscreva-se neste tema para receber novidades pelo site e por email.
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Fenando César Escobar
Mentor: Emiliano Chagas
Revisor: Rodrigo Morozetti Blanco
Especialista da área: Fernando Barnabé
Habilidades da BNCC
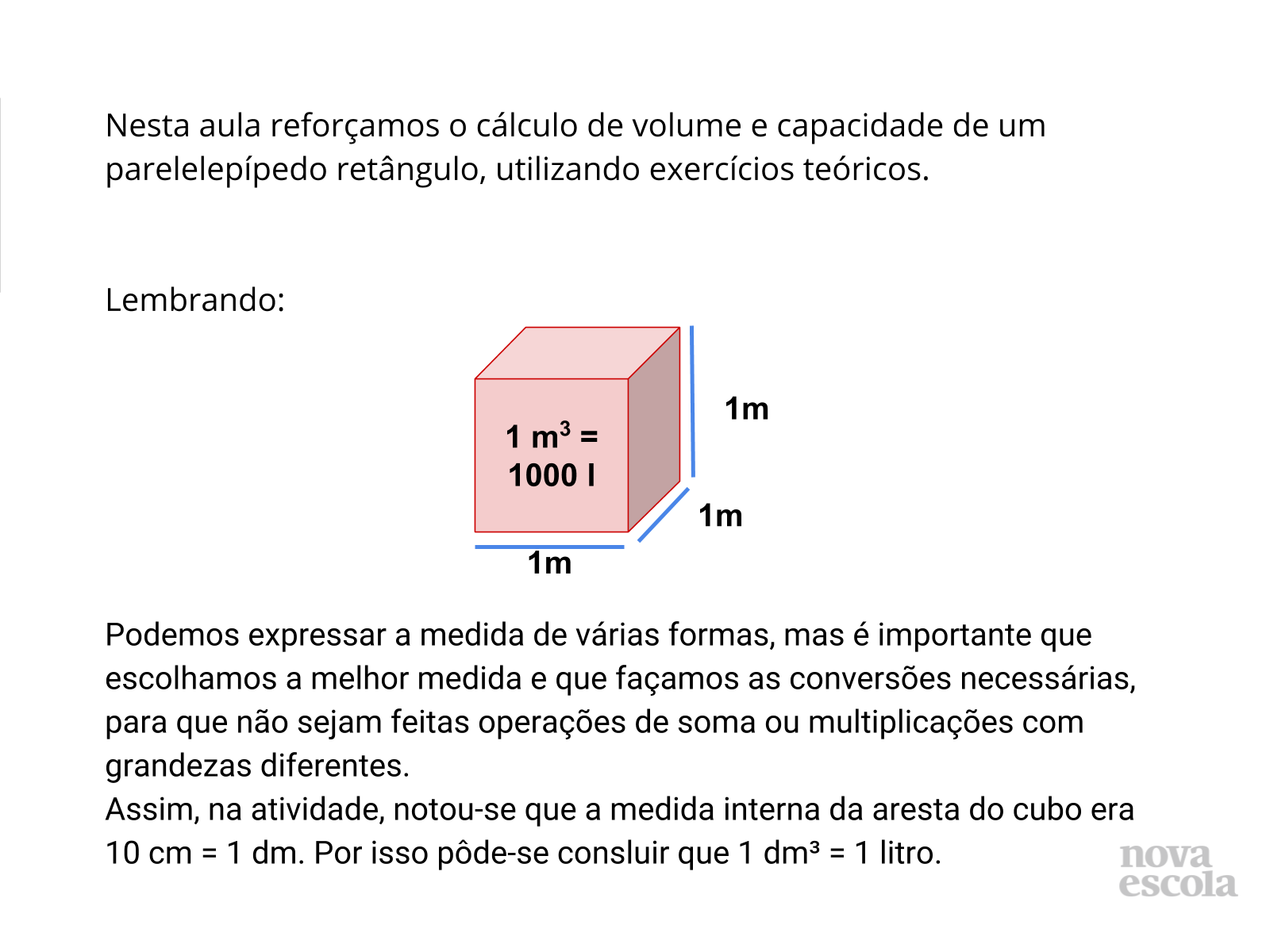
(EF08MA17) Reconhecer a relação entre um litro e um decímetro cúbico e a relação entre litro e metro cúbico, para resolver problemas de cálculo de capacidade de recipientes;
(EF08MA18) Resolver e elaborar problemas que envolvam o cálculo do volume de recipiente cujo formato é o de um bloco retangular.
Objetivos específicos
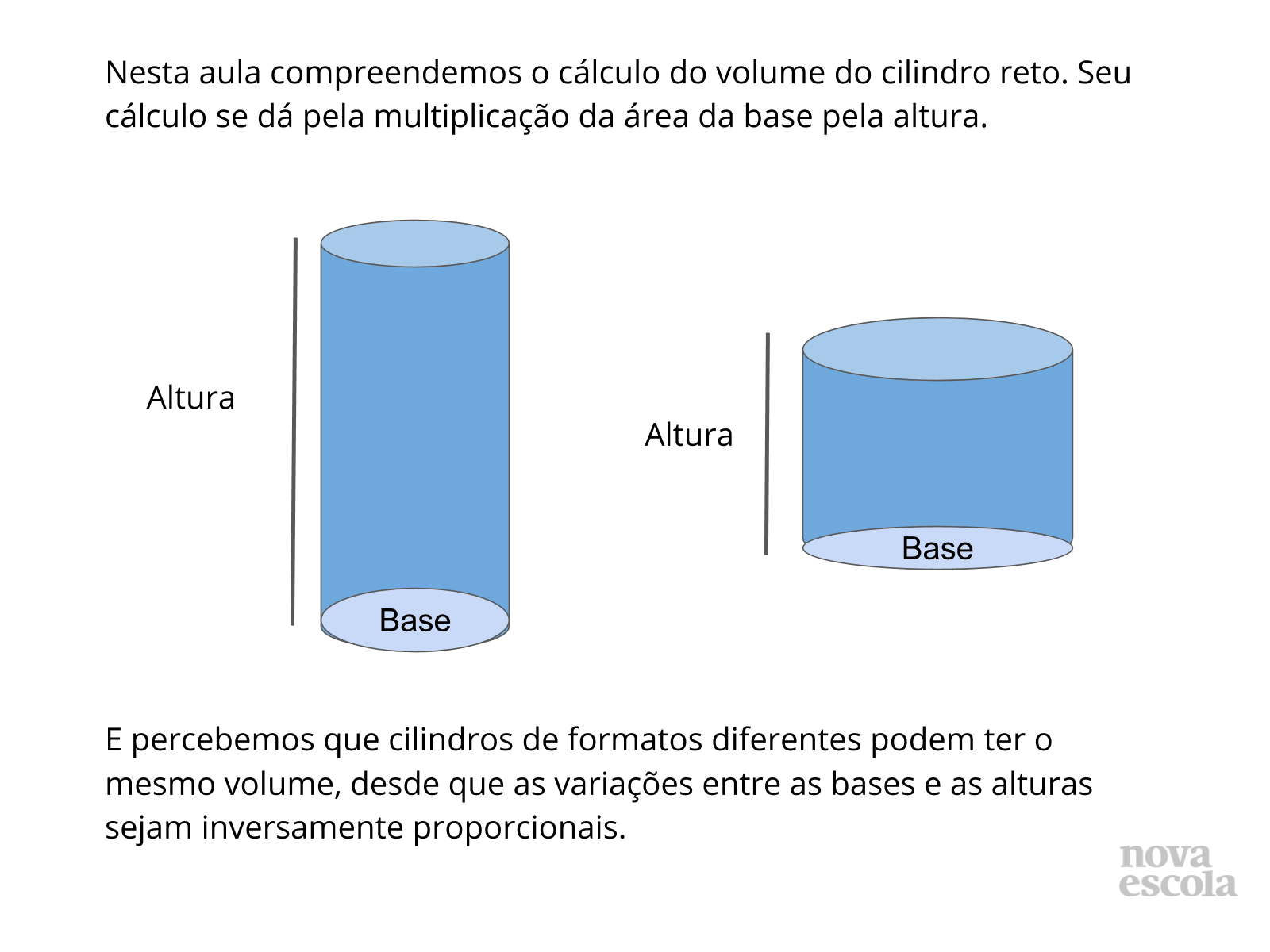
1. Compreender conceitualmente o cálculo do volume do cilindro reto;
2. Descrever as dimensões e características do? Cilindro Reto;
3. Efetuar cálculos? iniciais ?de volume do Cilindro Reto.
Conceito-chave
Volume do Cilindro Reto
Recursos necessários
Lápis, borracha, papel, .
Objetos cilíndricos: Latas de ervilhas, latas de goiabada, rolos de papel higiênico ou de papel toalha.
Habilidades BNCC:
Objetivos de aprendizagem
Planeje suas aulas pelo Whatsapp!
Qualidade com economia de tempo
Aula
Resumo da aula
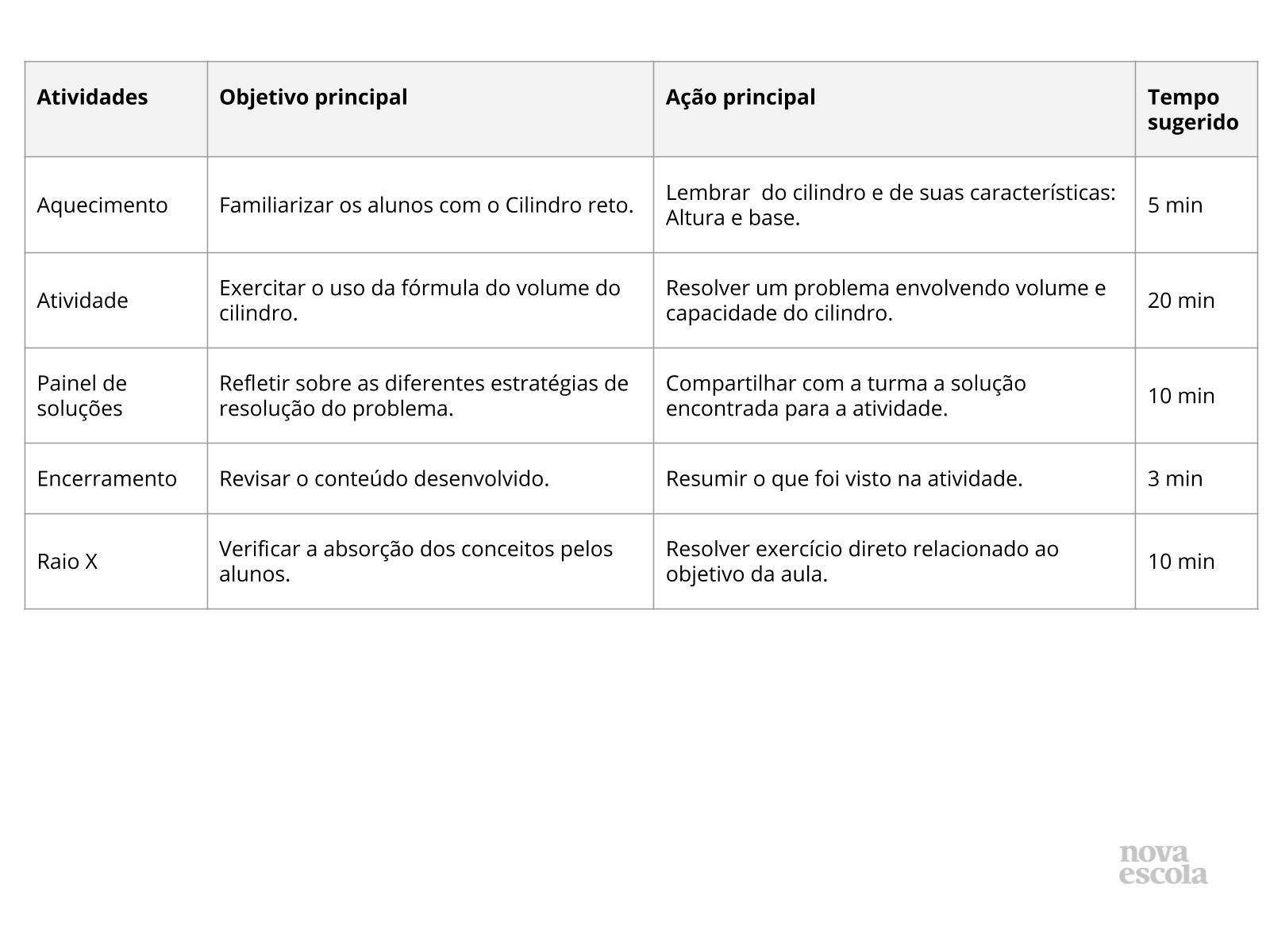Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo da aula
Tempo sugerido: 2 min
Orientação: Apresente a turma o que será feito, dando destaque ao fato de que o volume é o “espaço” que o cilindro reto ocupa e a capacidade é seu espaço interno.
Propósito: Compartilhar com a turma o objetivo da aula
Novo curso gratuito
Conheça nosso mais novo curso sobre adolescências, neurociência e engajamento nos anos finais
VER CURSO
