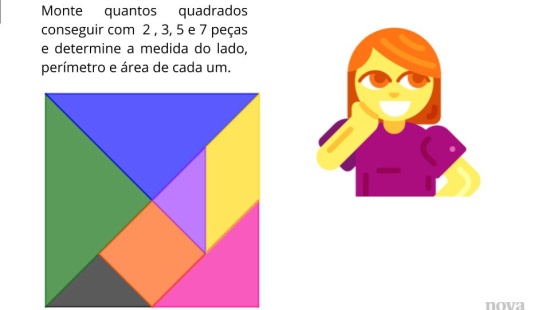
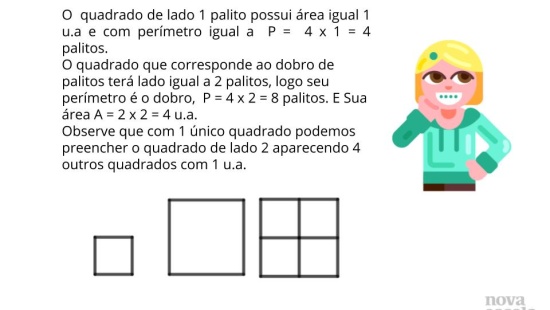
Raio X
Plano de Aula
Plano de aula: Explorando área e perímetro de um quadrado
Plano 1 de uma sequência de 5 planos. Veja todos os planos sobre Área e Perímetro do quadrado: quem é proporcional?
Por: Elizabeth Bento
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Elizabeth Bento
Mentor: Maria Aparecida Nemet Nascimento
Especialista de área: Fernando Barnabé
Habilidade da BNCC
(EF06MA27) Analisar e descrever as mudanças que ocorrem no perímetro e área de um quadrado quando ampliamos ou reduzimos seus lados por um fator k.
Habilidades necessárias
Determinar perímetro e área de um quadrilátero, reconhecer quando há proporcionalidade entre duas grandezas, compreender entes da geometria como ponto médio, diagonal e vértice.
Objetivos específicos
Concluir que apenas lado e perímetro de um quadrado são proporcionais.
Conceito-chave
Área, perímetro, proporcionalidade.
Recursos necessários
- Folha milimetrada;
- Lápis de cor;
- Tesoura;
- Transferidor;
- Régua.
Habilidades BNCC:
Objetivos de aprendizagem
Concluir que apenas lado e perímetro de um quadrado são proporcionais.
Resumo da aula
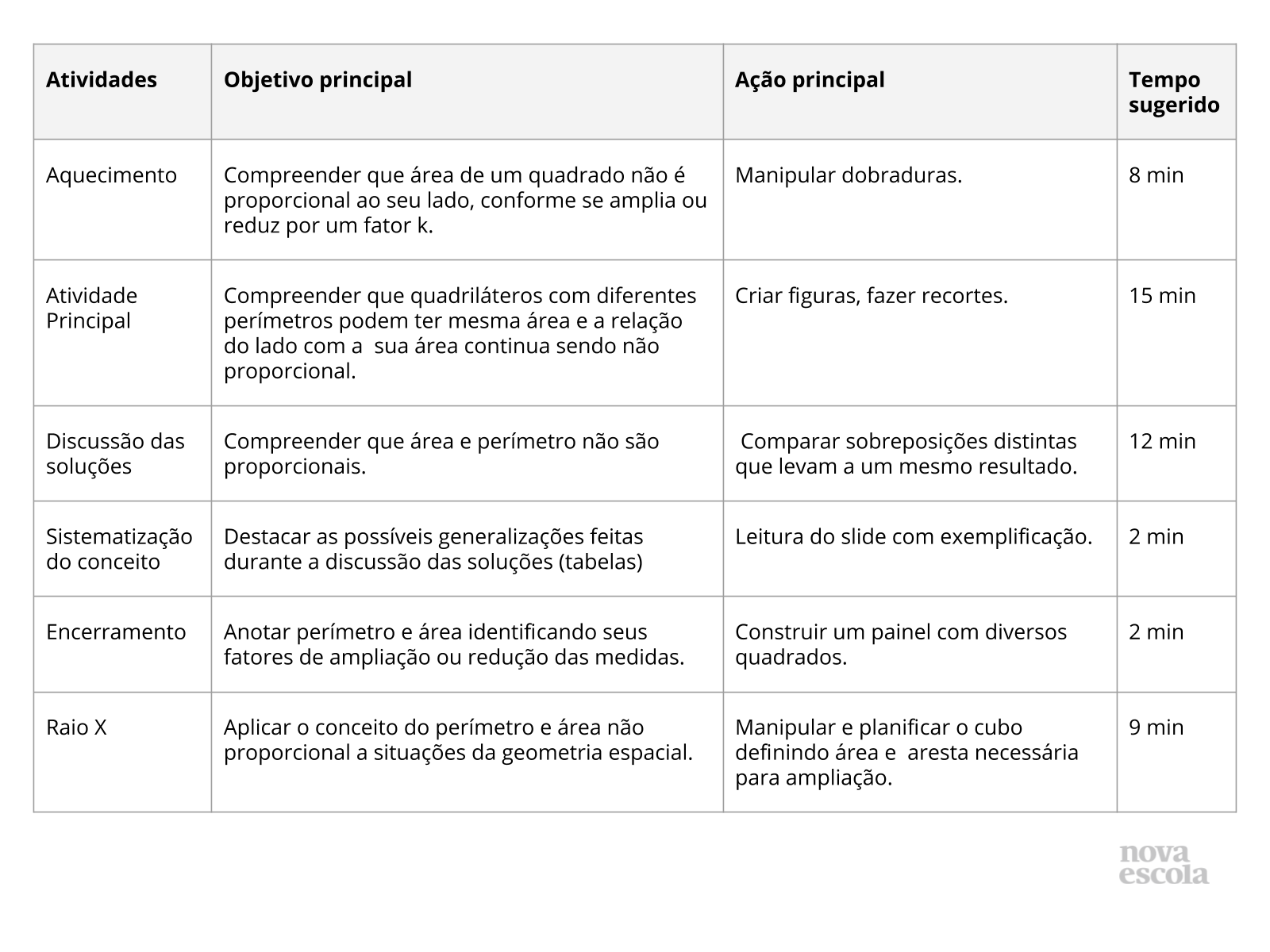
Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Compartilhe com a classe o objetivo desta aula.
Aquecimento: Origamis e quadrados (slides 3 ao 7)
Tempo sugerido: 8 minutos.
Orientação: Para esta atividade é necessário folha milimetrada, tesoura e lápis de cor. Distribua uma folha de papel milimetrado para cada aluno. O tamanho a ser construído do quadrado é livre, mas sugerimos que os alunos pensem em dois quadrados (sendo o segundo com o dobro da medida do lado) que caiba em uma única folha, reforçando deste modo o uso sustentável dos materiais.
Propósito: Analisar e compreender o que acontece com o perímetro e área de um quadrado quando ampliamos ou reduzimos seus lados.
Discuta com a turma:
- Como podemos garantir que os novos quadriláteros formados pelos recortes são quadrados ? É necessário que relembrem algumas propriedades dos quadrados: Os segmentos que ligam os vértices opostos AC e BD são as diagonais que se interceptam no centro do quadrado formando 4 ângulos de 90°. Essas diagonais são bissetrizes dos ângulos Â, B, C e D, com isso os 4 triângulos que se formam são isósceles e retângulos. Ao unir os triângulos a e c , b e d, verifica-se que o lado do antigo quadrado passa a ser a diagonal do novo quadrado e que os lados iguais dos triângulos passam a ser os lados dos novos quadrados. Formando deste modo 4 ângulos internos de 90° com 4 lados congruentes e dois a dois paralelos. Se necessário, acesse o Guia de Intervenções para relembrar as propriedades de um quadrado.
- O que acontece com área de um quadrado quando ampliamos ou reduzimos seus lados? A área é aumentada quando se amplia seus lados por qualquer fator e diminui quando reduz seu lado por qualquer fator.
- O que acontece com o perímetro de um quadrado quando ampliamos ou reduzimos seus lados O perímetro aumenta quando se amplia seus lados por qualquer fator e diminui quando reduz seu lado por qualquer fator.
- Existe alguma relação de proporcionalidade entre os lados e o perímetro? Sim. O perímetro fica igualmente ampliado ou reduzido pelo mesmo fator que ampliou ou reduziu os lados do quadrado.
- Existe alguma relação de proporcionalidade entre os lados e área? Não. A área não se amplia ou reduz a um mesmo fator que ampliou ou reduziu a medida dos lados.
Materiais complementares para impressão:
Aquecimento: Origamis e quadrados (slides 3 ao 7)
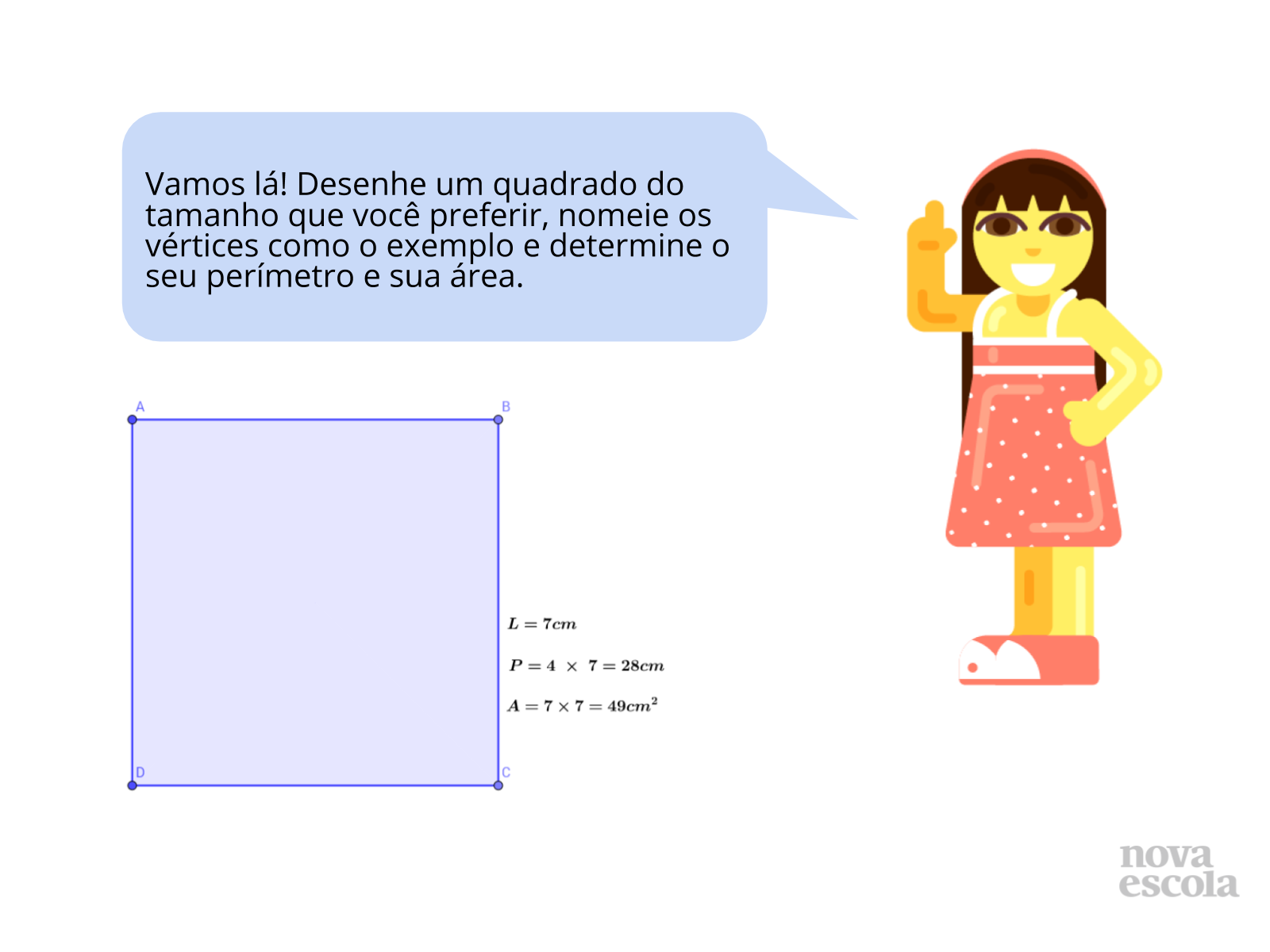
Tempo sugerido: 8 minutos.
Orientação: Para esta atividade é necessário folha milimetrada, tesoura e lápis de cor. Distribua uma folha de papel milimetrado para cada aluno. O tamanho a ser construído do quadrado é livre, mas sugerimos que os alunos pensem em dois quadrados (sendo o segundo com o dobro da medida do lado) que caiba em uma única folha, reforçando deste modo o uso sustentável dos materiais.
Propósito: Analisar e compreender o que acontece com o perímetro e área de um quadrado quando ampliamos ou reduzimos seus lados.
Discuta com a turma:
- Como podemos garantir que os novos quadriláteros formados pelos recortes são quadrados ? É necessário que relembrem algumas propriedades dos quadrados: Os segmentos que ligam os vértices opostos AC e BD são as diagonais que se interceptam no centro do quadrado formando 4 ângulos de 90°. Essas diagonais são bissetrizes dos ângulos Â, B, C e D, com isso os 4 triângulos que se formam são isósceles e retângulos. Ao unir os triângulos a e c , b e d, verifica-se que o lado do antigo quadrado passa a ser a diagonal do novo quadrado e que os lados iguais dos triângulos passam a ser os lados dos novos quadrados. Formando deste modo 4 ângulos internos de 90° com 4 lados congruentes e dois a dois paralelos. Se necessário, acesse o Guia de Intervenções para relembrar as propriedades de um quadrado.
- O que acontece com área de um quadrado quando ampliamos ou reduzimos seus lados? A área é aumentada quando se amplia seus lados por qualquer fator e diminui quando reduz seu lado por qualquer fator.
- O que acontece com o perímetro de um quadrado quando ampliamos ou reduzimos seus lados O perímetro aumenta quando se amplia seus lados por qualquer fator e diminui quando reduz seu lado por qualquer fator.
- Existe alguma relação de proporcionalidade entre os lados e o perímetro? Sim. O perímetro fica igualmente ampliado ou reduzido pelo mesmo fator que ampliou ou reduziu os lados do quadrado.
- Existe alguma relação de proporcionalidade entre os lados e área? Não. A área não se amplia ou reduz a um mesmo fator que ampliou ou reduziu a medida dos lados.
Aquecimento: Origamis e quadrados (slides 3 ao 7)
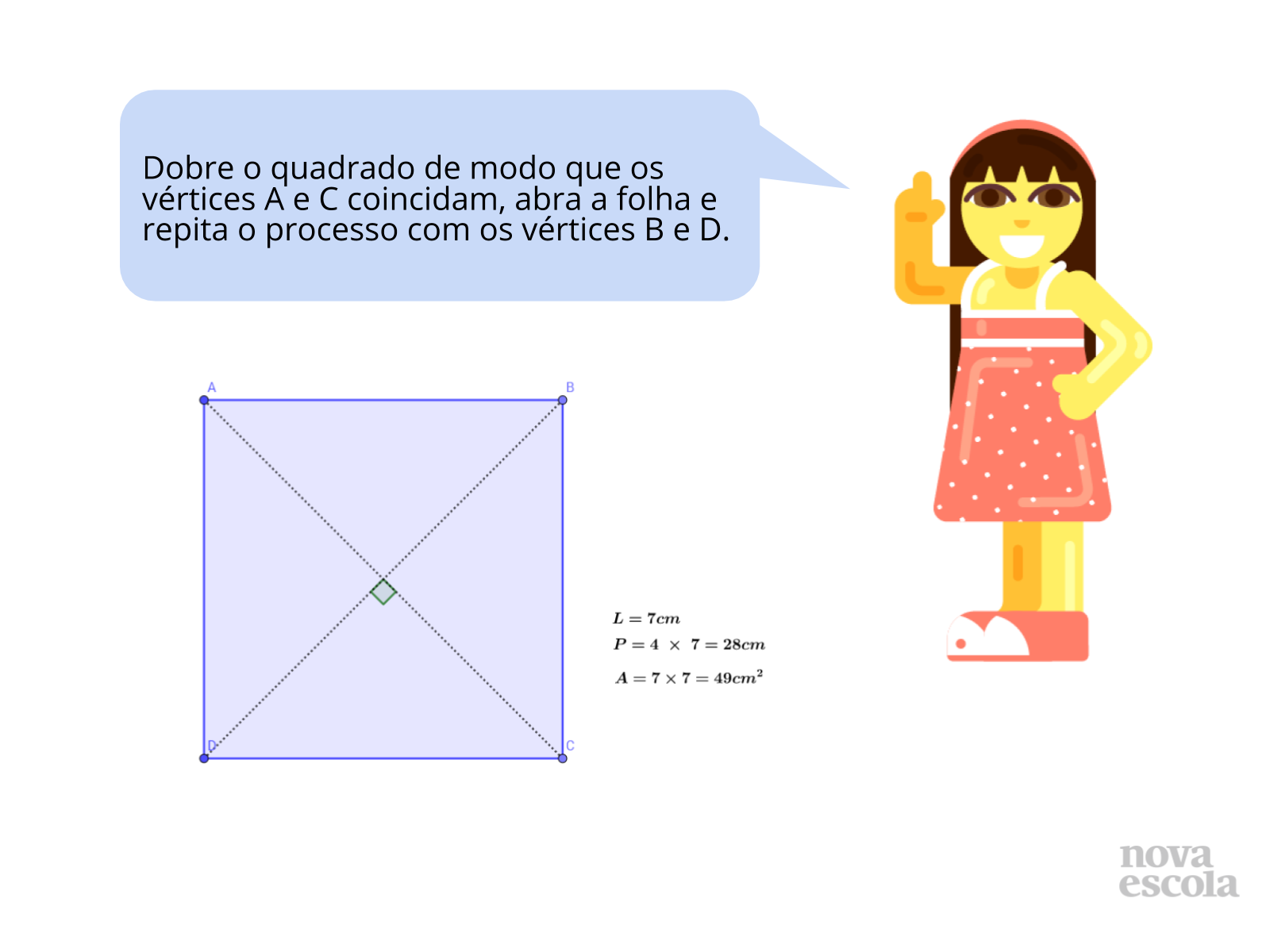
Tempo sugerido: 8 minutos.
Orientação: Para esta atividade é necessário folha milimetrada, tesoura e lápis de cor. Distribua uma folha de papel milimetrado para cada aluno. O tamanho a ser construído do quadrado é livre, mas sugerimos que os alunos pensem em dois quadrados (sendo o segundo com o dobro da medida do lado) que caiba em uma única folha, reforçando deste modo o uso sustentável dos materiais.
Propósito: Analisar e compreender o que acontece com o perímetro e área de um quadrado quando ampliamos ou reduzimos seus lados.
Discuta com a turma:
- Como podemos garantir que os novos quadriláteros formados pelos recortes são quadrados ? É necessário que relembrem algumas propriedades dos quadrados: Os segmentos que ligam os vértices opostos AC e BD são as diagonais que se interceptam no centro do quadrado formando 4 ângulos de 90°. Essas diagonais são bissetrizes dos ângulos Â, B, C e D, com isso os 4 triângulos que se formam são isósceles e retângulos. Ao unir os triângulos a e c , b e d, verifica-se que o lado do antigo quadrado passa a ser a diagonal do novo quadrado e que os lados iguais dos triângulos passam a ser os lados dos novos quadrados. Formando deste modo 4 ângulos internos de 90° com 4 lados congruentes e dois a dois paralelos. Se necessário, acesse o Guia de Intervenções para relembrar as propriedades de um quadrado.
- O que acontece com área de um quadrado quando ampliamos ou reduzimos seus lados? A área é aumentada quando se amplia seus lados por qualquer fator e diminui quando reduz seu lado por qualquer fator.
- O que acontece com o perímetro de um quadrado quando ampliamos ou reduzimos seus lados O perímetro aumenta quando se amplia seus lados por qualquer fator e diminui quando reduz seu lado por qualquer fator.
- Existe alguma relação de proporcionalidade entre os lados e o perímetro? Sim. O perímetro fica igualmente ampliado ou reduzido pelo mesmo fator que ampliou ou reduziu os lados do quadrado.
- Existe alguma relação de proporcionalidade entre os lados e área? Não. A área não se amplia ou reduz a um mesmo fator que ampliou ou reduziu a medida dos lados.
Aquecimento: Origamis e quadrados (slides 3 ao 7)
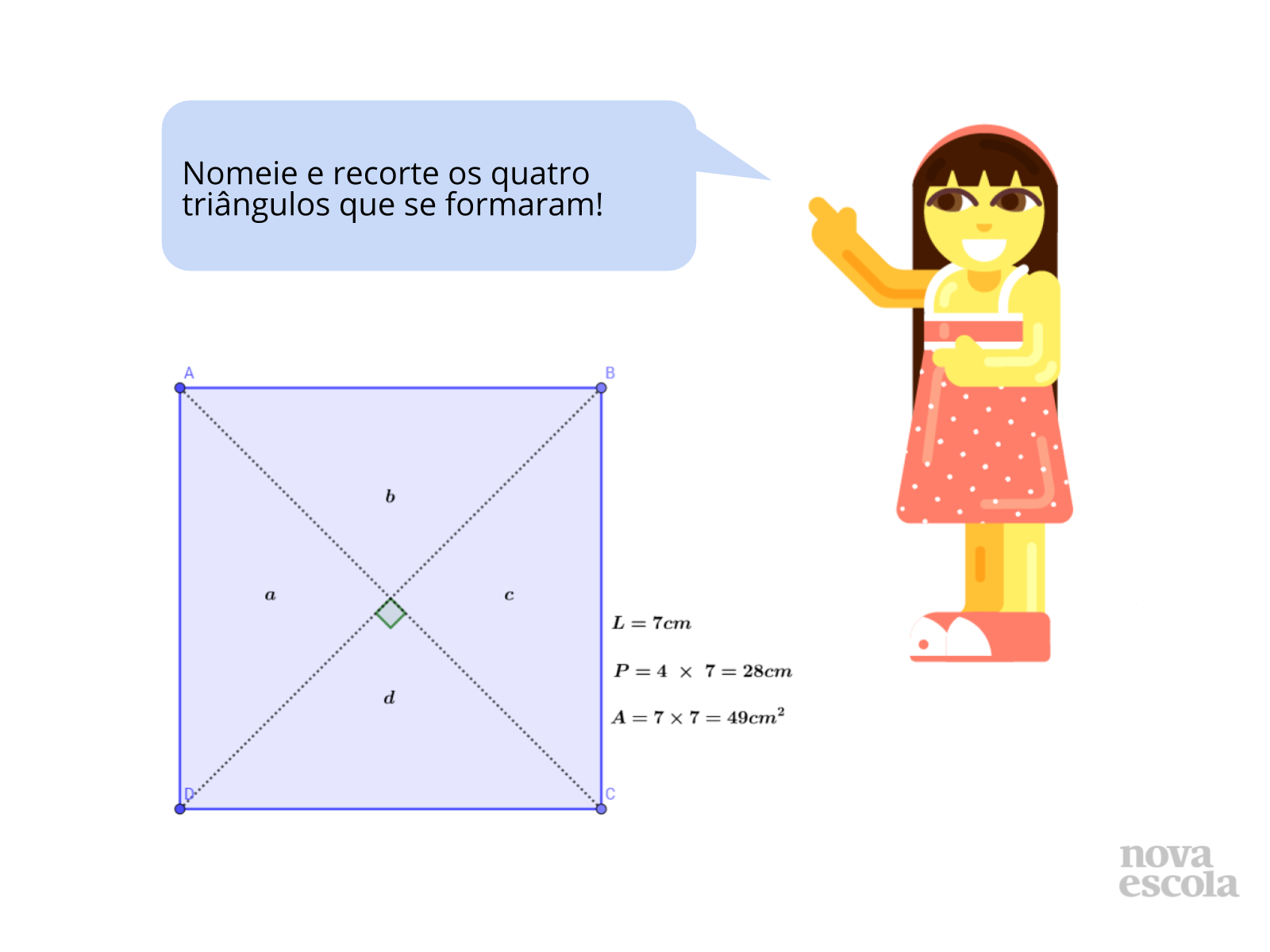
Tempo sugerido: 8 minutos.
Orientação: Para esta atividade é necessário folha milimetrada, tesoura e lápis de cor. Distribua uma folha de papel milimetrado para cada aluno. O tamanho a ser construído do quadrado é livre, mas sugerimos que os alunos pensem em dois quadrados (sendo o segundo com o dobro da medida do lado) que caiba em uma única folha, reforçando deste modo o uso sustentável dos materiais.
Propósito: Analisar e compreender o que acontece com o perímetro e área de um quadrado quando ampliamos ou reduzimos seus lados.
Discuta com a turma:
- Como podemos garantir que os novos quadriláteros formados pelos recortes são quadrados ? É necessário que relembrem algumas propriedades dos quadrados: Os segmentos que ligam os vértices opostos AC e BD são as diagonais que se interceptam no centro do quadrado formando 4 ângulos de 90°. Essas diagonais são bissetrizes dos ângulos Â, B, C e D, com isso os 4 triângulos que se formam são isósceles e retângulos. Ao unir os triângulos a e c , b e d, verifica-se que o lado do antigo quadrado passa a ser a diagonal do novo quadrado e que os lados iguais dos triângulos passam a ser os lados dos novos quadrados. Formando deste modo 4 ângulos internos de 90° com 4 lados congruentes e dois a dois paralelos. Se necessário, acesse o Guia de Intervenções para relembrar as propriedades de um quadrado.
- O que acontece com área de um quadrado quando ampliamos ou reduzimos seus lados? A área é aumentada quando se amplia seus lados por qualquer fator e diminui quando reduz seu lado por qualquer fator.
- O que acontece com o perímetro de um quadrado quando ampliamos ou reduzimos seus lados O perímetro aumenta quando se amplia seus lados por qualquer fator e diminui quando reduz seu lado por qualquer fator.
- Existe alguma relação de proporcionalidade entre os lados e o perímetro? Sim. O perímetro fica igualmente ampliado ou reduzido pelo mesmo fator que ampliou ou reduziu os lados do quadrado.
- Existe alguma relação de proporcionalidade entre os lados e área? Não. A área não se amplia ou reduz a um mesmo fator que ampliou ou reduziu a medida dos lados.
Aquecimento: Origamis e quadrados (slides 3 ao 7)
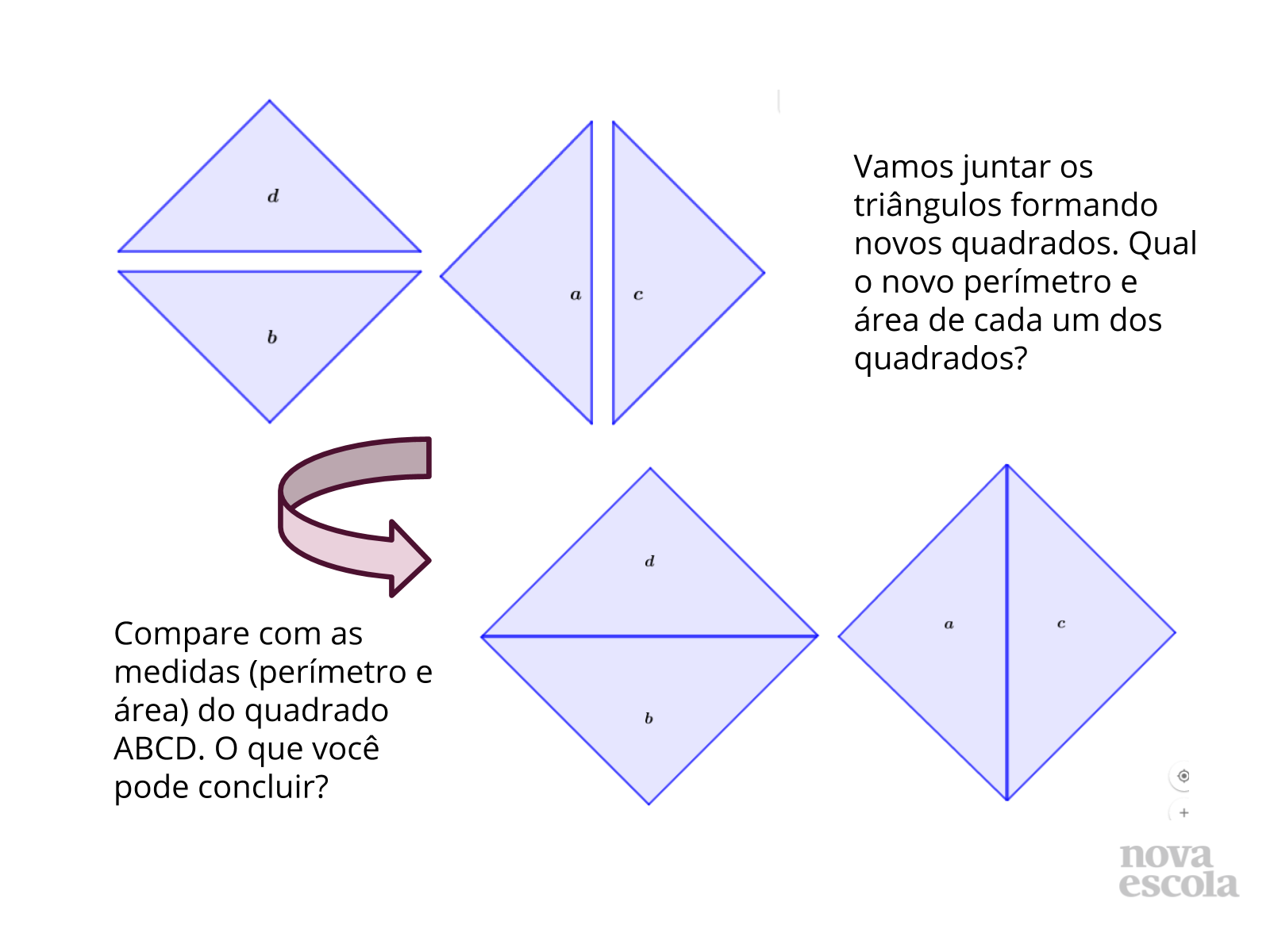
Tempo sugerido: 8 minutos.
Orientação: Para esta atividade é necessário folha milimetrada, tesoura e lápis de cor. Distribua uma folha de papel milimetrado para cada aluno. O tamanho a ser construído do quadrado é livre, mas sugerimos que os alunos pensem em em dois quadrados (sendo o segundo com o dobro da medida do lado) que caiba em uma única folha, reforçando deste modo o uso sustentável dos materiais.
Propósito: Analisar e compreender o que acontece com o perímetro e área de um quadrado quando ampliamos ou reduzimos seus lados.
Discuta com a turma:
- Como podemos garantir que os novos quadriláteros formados pelos recortes são quadrados ? É necessário que relembrem algumas propriedades dos quadrados: Os segmentos que ligam os vértices opostos AC e BD são as diagonais que se interceptam no centro do quadrado formando 4 ângulos de 90°. Essas diagonais são bissetrizes dos ângulos Â, B, C e D, com isso os 4 triângulos que se formam são isósceles e retângulos. Ao unir os triângulos a e c , b e d, verifica- se que o lado do antigo quadrado passa a ser a diagonal do novo quadrado e que os lados iguais dos triângulos passam a ser os lados dos novos quadrados. Formando deste modo 4 ângulos internos de 90° com 4 lados congruentes e dois a dois paralelos. Se necessário acesse o guia de intervenções para relembrar as propriedades de um quadrado.
- O que acontece com área de um quadrado quando ampliamos ou reduzimos seus lados? A área é aumentada quando se amplia seus lados por qualquer fator e diminui quando reduz seu lado por qualquer fator.
- O que acontece com o perímetro de um quadrado quando ampliamos ou reduzimos seus lados O perímetro aumenta quando se amplia seus lados por qualquer fator e diminui quando reduz seu lado por qualquer fator.
- Existe alguma relação de proporcionalidade entre os lados e o perímetro? Sim. O perímetro fica igualmente ampliado ou reduzido pelo mesmo fator que ampliou ou reduziu os lados do quadrado.
- Existe alguma relação de proporcionalidade entre os lados e área? Não. A área não amplia ou reduz a um mesmo fator que ampliou ou reduziu a medida dos lados
Aquecimento: Origamis e quadrados
Tempo sugerido: 8 minutos.
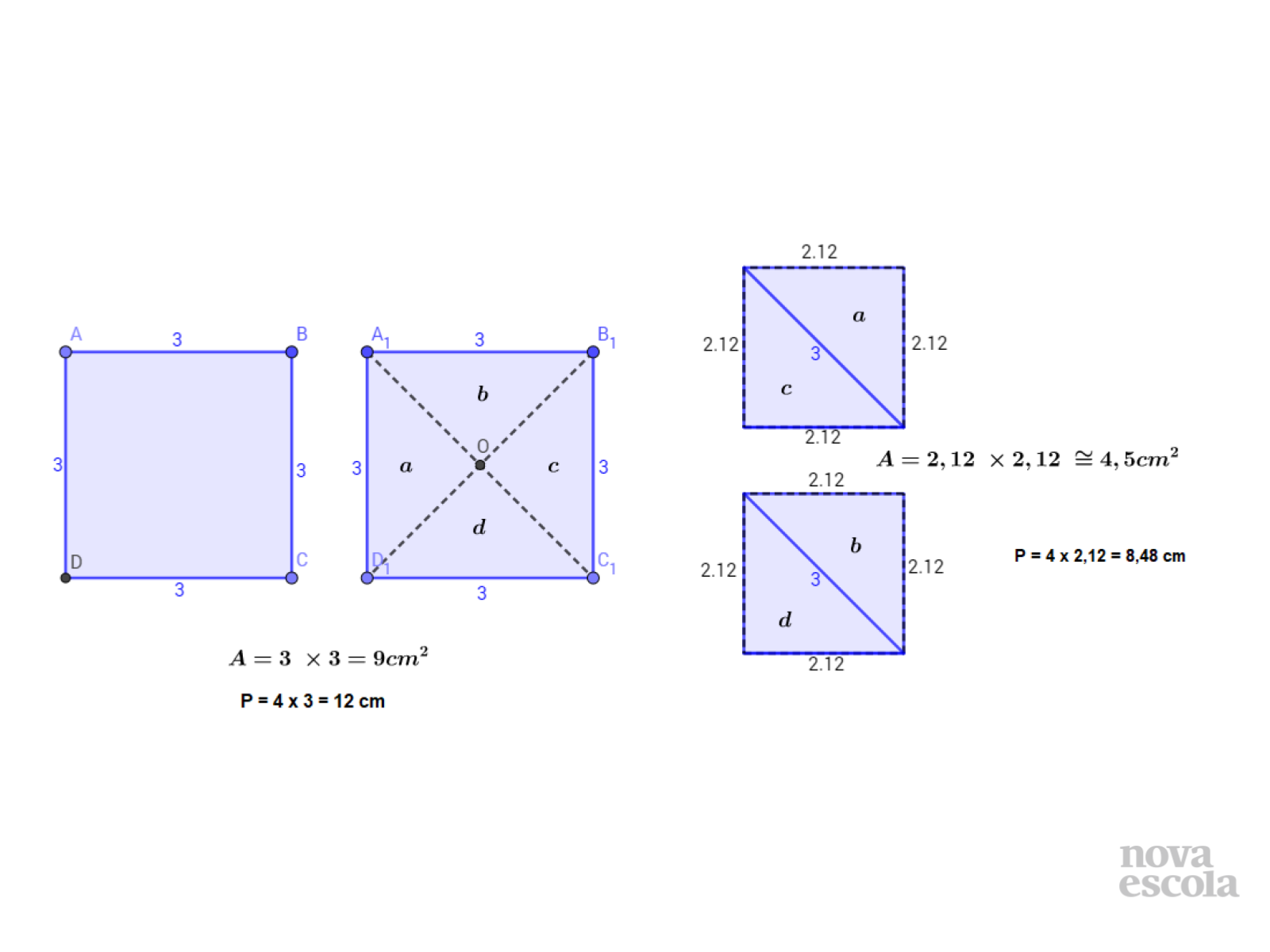
Orientação: Apresentamos a resolução com dois quadrados distintos, mas você pode fazer um quadrado maior ou menor se preferir na lousa. Caso haja necessidade de construir uma solução na lousa será necessário utilizar um compasso e régua para lousa.
Propósito: Analisar e compreender o que acontece com o perímetro e área de um quadrado quando ampliamos ou reduzimos seus lados.
Discuta com a turma:
- Que tipo de generalização podemos realizar com os resultados obtidos? Para todo e qualquer quadrado ampliar ou reduzir seu lado por um fator k a área não fica multiplicada por esse mesmo fator k, que é o que caracteriza se duas grandezas são diretamente proporcionais ou não. Se necessário consulte o Guia de Intervenções.
- Sabemos que a área não é proporcional ao lado quando ampliamos ou reduzimos este mesmo por fator k. Mas podemos estabelecer um padrão de aumento ou redução? Se sim qual? Justifique. Observe a tabela nos slides 10 e 11. Podemos generalizar a ampliação de um quadrado escrevendo o produto do fator que amplia ou reduz os lados ao quadrado por uma área em questão. Use a tabela para reforçar a não proporcionalidade e para compreender o padrão existente quando analisamos os perímetros e as áreas de regiões quadradas.
Aquecimento: Origamis e quadrados
Tempo sugerido: 8 minutos.
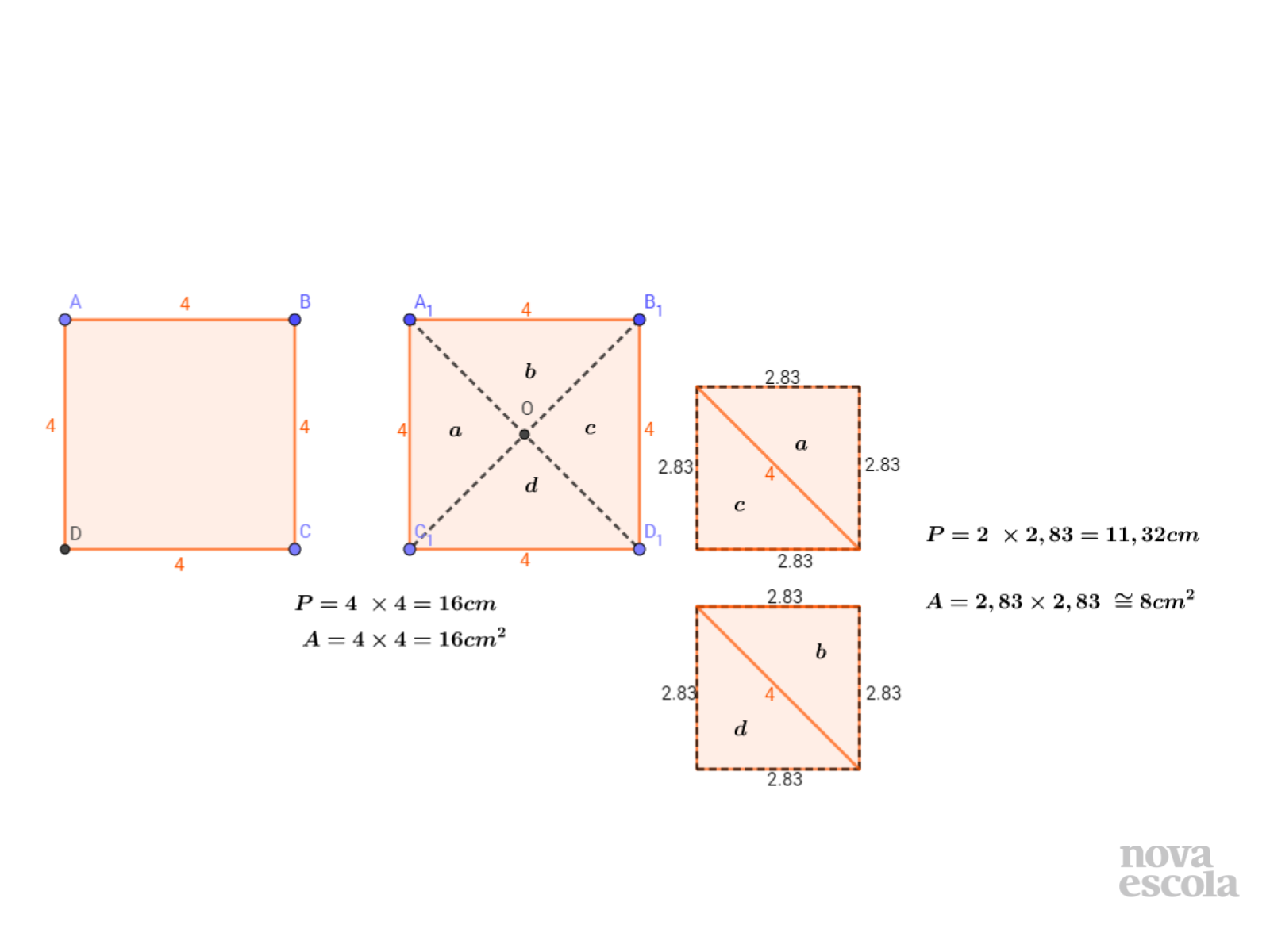
Orientação: Apresentamos a resolução com dois quadrados distintos, mas você pode fazer um quadrado maior ou menor se preferir na lousa. Caso haja necessidade de construir uma solução na lousa será necessário utilizar um compasso e régua para lousa.
Propósito: Analisar e compreender o que acontece com o perímetro e área de um quadrado quando ampliamos ou reduzimos seus lados.
Discuta com a turma:
- Que tipo de generalização podemos realizar com os resultados obtidos? Para todo e qualquer quadrado ampliar ou reduzir seu lado por um fator k a área não fica multiplicada por esse mesmo fator k, que é o que caracteriza se duas grandezas são diretamente proporcionais ou não. Se necessário consulte o Guia de Intervenções.
- Sabemos que a área não é proporcional ao lado quando ampliamos ou reduzimos este mesmo por fator k. Mas podemos estabelecer um padrão de aumento ou redução? Se sim qual? Justifique. Observe a tabela nos slides 10 e 11. Podemos generalizar a ampliação de um quadrado escrevendo o produto do fator que amplia ou reduz os lados ao quadrado por uma área em questão. Use a tabela para reforçar a não proporcionalidade e para compreender o padrão existente quando analisamos os perímetros e as áreas de regiões quadradas.
Aquecimento: Origamis e quadrados
Tempo sugerido: 8 minutos
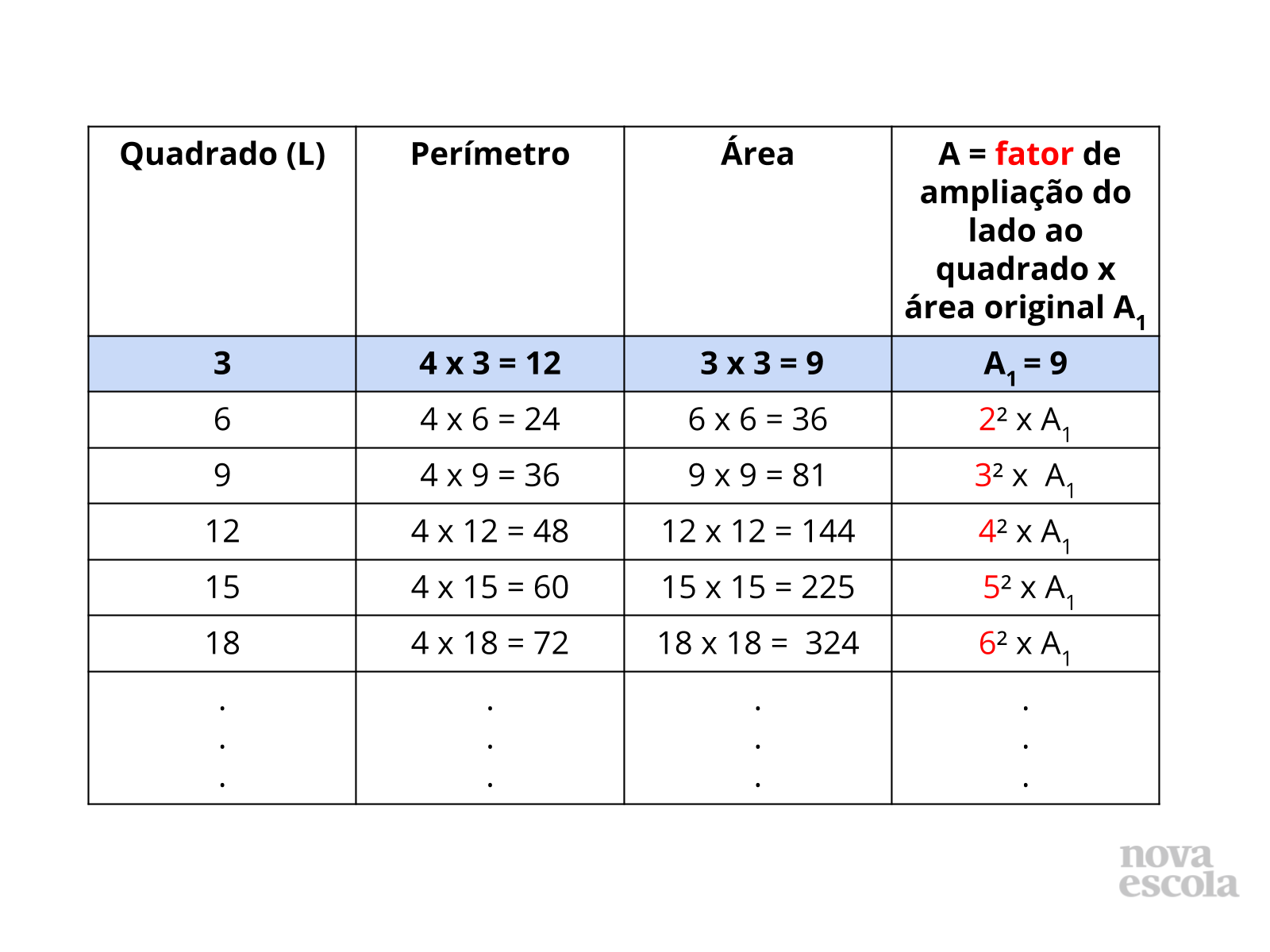
Orientação: Apresentamos a resolução com dois quadrados distintos, mas você pode fazer um quadrado maior ou menor se preferir na lousa. Caso haja necessidade de construir uma solução na lousa será necessário utilizar um compasso e régua para lousa.
Propósito: Analisar e compreender o que acontece com o perímetro e área de um quadrado quando ampliamos ou reduzimos seus lados.
Discuta com a turma:
- Que tipo de generalização podemos realizar com os resultados obtidos? Para todo e qualquer quadrado ampliar ou reduzir seu lado por um fator k a área não fica multiplicada por esse mesmo fator k, que é o que caracteriza se duas grandezas são diretamente proporcionais ou não. Se necessário consulte o guia de intervenções.
- Sabemos que a área não é proporcional ao lado quando ampliamos ou reduzimos este mesmo por fator k. Mas podemos estabelecer um padrão de aumento ou redução? Se sim qual? Justifique. Observe a tabela nos slides 10 e 11. Podemos generalizar a ampliação de um quadrado escrevendo o produto do fator que amplia ou reduz os lados ao quadrado por uma área em questão. Use a tabela para reforçar a não proporcionalidade e para compreender o padrão existente quando analisamos os perímetros e as áreas de regiões quadradas.
Aquecimento: Origamis e quadrados
Tempo sugerido: 8 minutos.
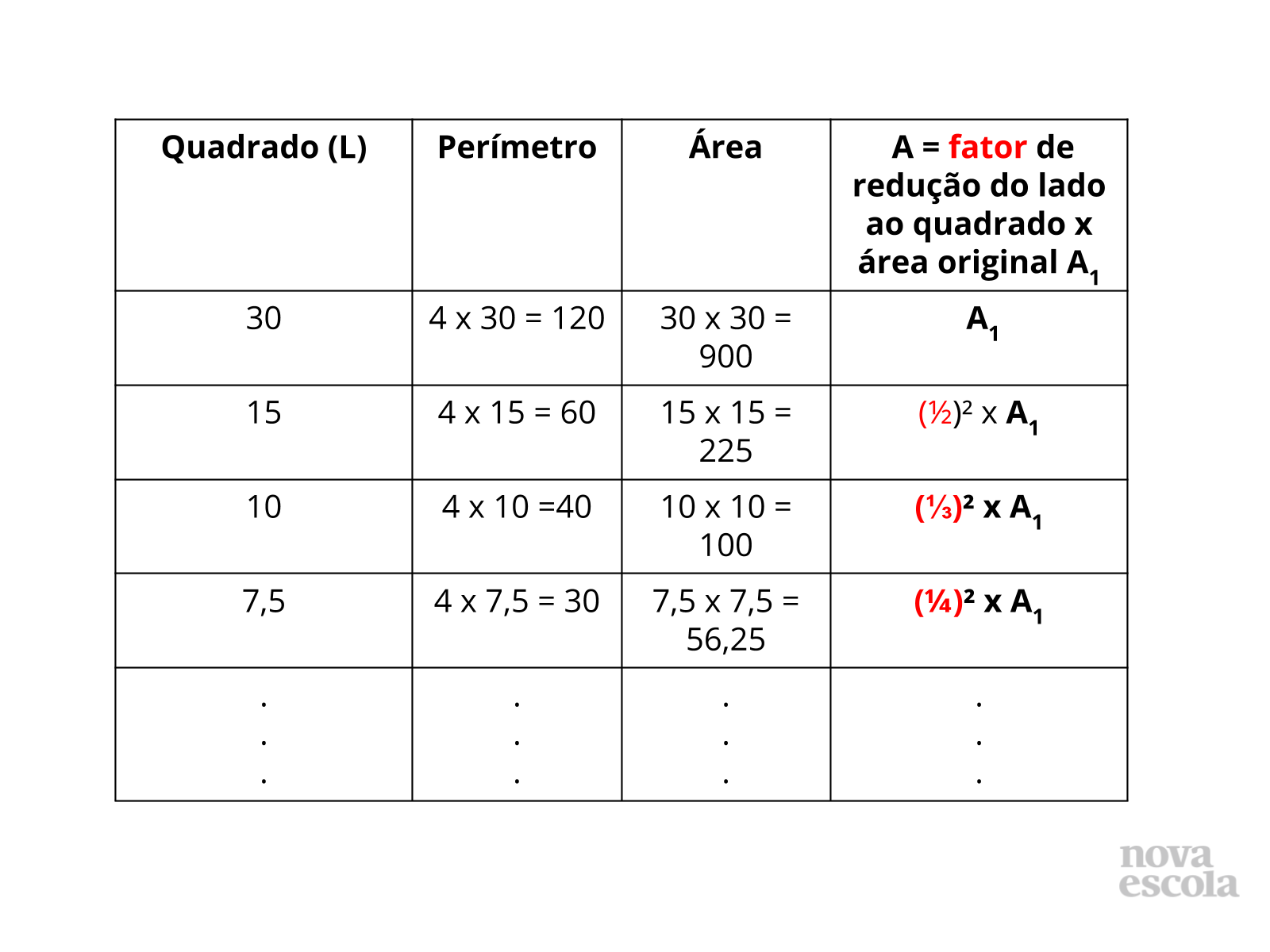
Orientação: Apresentamos a resolução com dois quadrados distintos, mas você pode fazer um quadrado maior ou menor se preferir na lousa. Caso haja necessidade de construir uma solução na lousa será necessário utilizar um compasso e régua para lousa.
Propósito: Analisar e compreender o que acontece com o perímetro e área de um quadrado quando ampliamos ou reduzimos seus lados.
Discuta com a turma:
- Que tipo de generalização podemos realizar com os resultados obtidos? Para todo e qualquer quadrado ampliar ou reduzir seu lado por um fator k a área não fica multiplicada por esse mesmo fator k, que é o que caracteriza se duas grandezas são diretamente proporcionais ou não. Se necessário consulte o Guia de Intervenções.
- Sabemos que a área não é proporcional ao lado quando ampliamos ou reduzimos este mesmo por fator k. Mas podemos estabelecer um padrão de aumento ou redução? Se sim qual? Justifique. Observe a tabela nos slides 10 e 11. Podemos generalizar a ampliação de um quadrado escrevendo o produto do fator que amplia ou reduz os lados ao quadrado por uma área em questão. Use a tabela para reforçar a não proporcionalidade e para compreender o padrão existente quando analisamos os perímetros e as áreas de regiões quadradas.
Atividade Principal: Sobreposição de quadriláteros 1 (slides 12 e 13)

Tempo sugerido: 15 minutos.
Orientação: Distribua uma folha milimetrada para cada aluno. Sugira que façam diversos tipos de sobreposição sem dobrar os quadriláteros, e que escolha uma para resolver a questão acima do slide.
Propósito: Investigar e determinar o lado de quadriláteros sobrepostos a partir da área e do perímetro. Constatar que figuras com perímetros diferentes podem possuir mesma área.
Discuta com a turma:
- Quaisquer sobreposições escolhidas terão as mesmas medidas? Apesar do enunciado exigir que a sobreposição ocorra de maneira paralela e que partes dos segmentos paralelos deverão estar contidos no mesmo plano, é possível que algum aluno sobreponha com inclinação, e por esse motivo essa observação deve ser pautada a fim de verificar que a área e o perímetro irá mudar.
- Temos dois quadriláteros diferentes com áreas iguais, como isso é possível? Apesar da diferença de lados a área poder numericamente igual e pode ser verificada através da quadriculação do polígono (verifique guia de intervenções aqui) no caso dos quadriláteros que a área é dada pelo produto da base pela altura, podemos listar diversos fatores inteiros ou não que resultam num mesmo valor.
- Quaisquer pares de quadriláteros que possuírem a mesma área, quando sobrepostos terão o perímetro numericamente igual à área? Não, o perímetro depende unicamente do tipo de sobreposição.
Materiais complementares para impressão:
Sobreposição de quadriláteros 1 (slides 12 e 13)
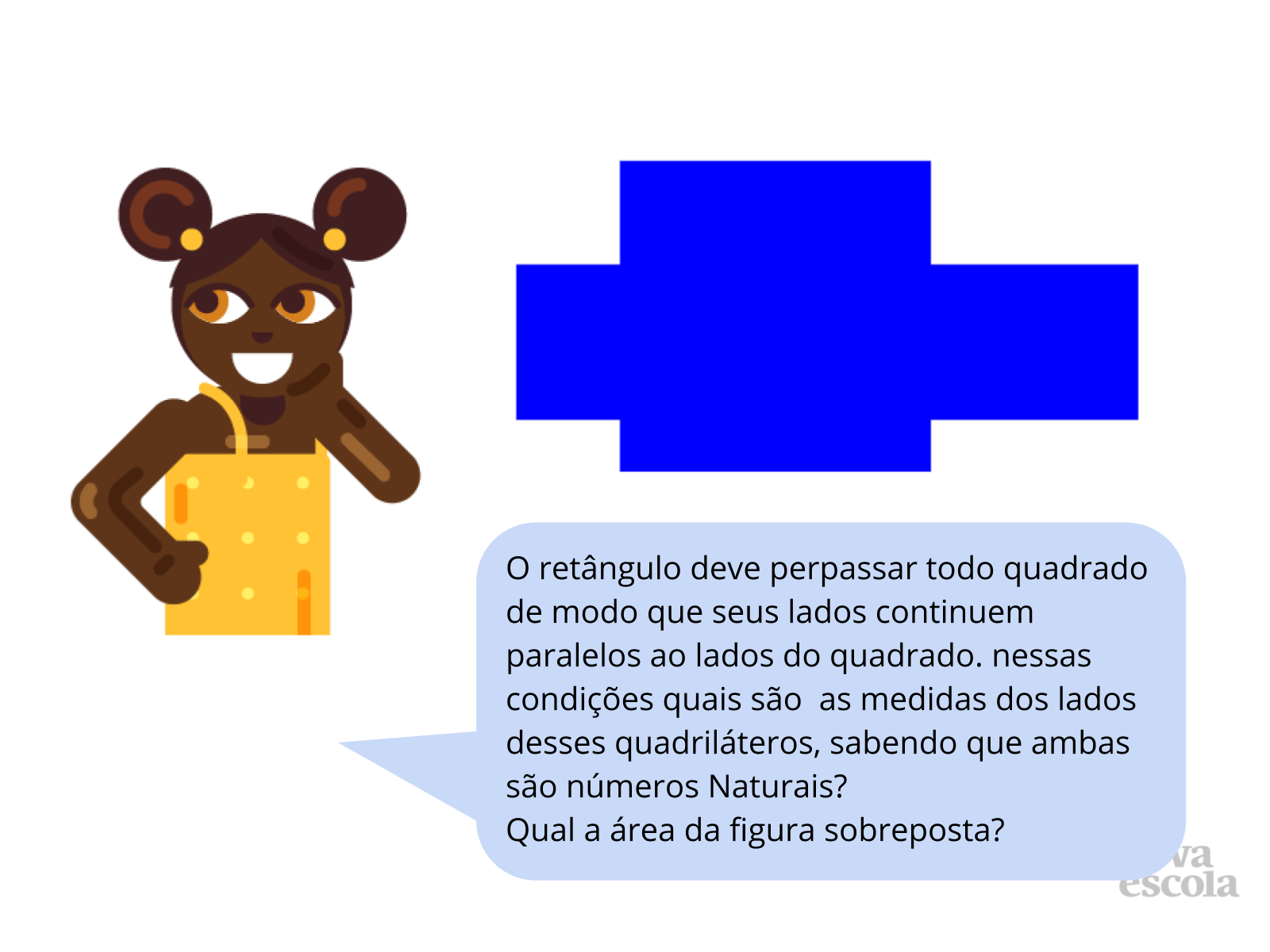
Tempo sugerido: 15 minutos.
Orientação: Distribua uma folha milimetrada para cada aluno. Sugira que façam diversos tipos de sobreposição sem dobrar os quadriláteros, e que escolha uma para resolver a questão acima do slide.
Propósito: Investigar e determinar o lado de quadriláteros sobrepostos a partir da área e do perímetro. Constatar que figuras com perímetros diferentes podem possuir mesma área.
Discuta com a turma:
- Quaisquer sobreposições escolhidas terão as mesmas medidas? Apesar do enunciado exigir que a sobreposição ocorra de maneira paralela e que partes dos segmentos paralelos deverão estar contidos no mesmo plano, é possível que algum aluno sobreponha com inclinação, e por esse motivo essa observação deve ser pautada a fim de verificar que a área e o perímetro irá mudar.
- Temos dois quadriláteros diferentes com áreas iguais, como isso é possível? Apesar da diferença de lados a área poder numericamente igual e pode ser verificada através da quadriculação do polígono (verifique guia de intervenções aqui) no caso dos quadriláteros que a área é dada pelo produto da base pela altura, podemos listar diversos fatores inteiros ou não que resultam num mesmo valor.
- Quaisquer pares de quadriláteros que possuírem a mesma área, quando sobrepostos terão o perímetro numericamente igual à área? Não, o perímetro nesse caso depende unicamente do tipo de sobreposição.
Sobreposição de quadriláteros 2 ( slides 14 e 15)

Tempo sugerido: 15 minutos.
Orientação: Na mesma folha milimetrada peça para que construam duas figuras ampliadas pelo fator 2
Propósito: Constatar que área do quadrado ou retângulo não é proporcional ao seu lado.
Discuta com a turma:
- O perímetro do retângulo é proporcional ao seu lado? Sim, o perímetro é ampliado ou reduzido pelo mesmo fator ampliou ou reduziu os lados do mesmo.
- A área do retângulo é proporcional ao seu lado? Não, observa-se que não há um fator constante de proporcionalidade entre o lado e área.
- É possível generalizar a área de um retângulo estabelecendo uma correspondência com o fator de ampliação ou redução? Sim, do mesmo modo observado nas tabelas criadas para o quadrado (slides 10 e 11)
Sobreposição de quadriláteros 2 ( slides 14 e 15)
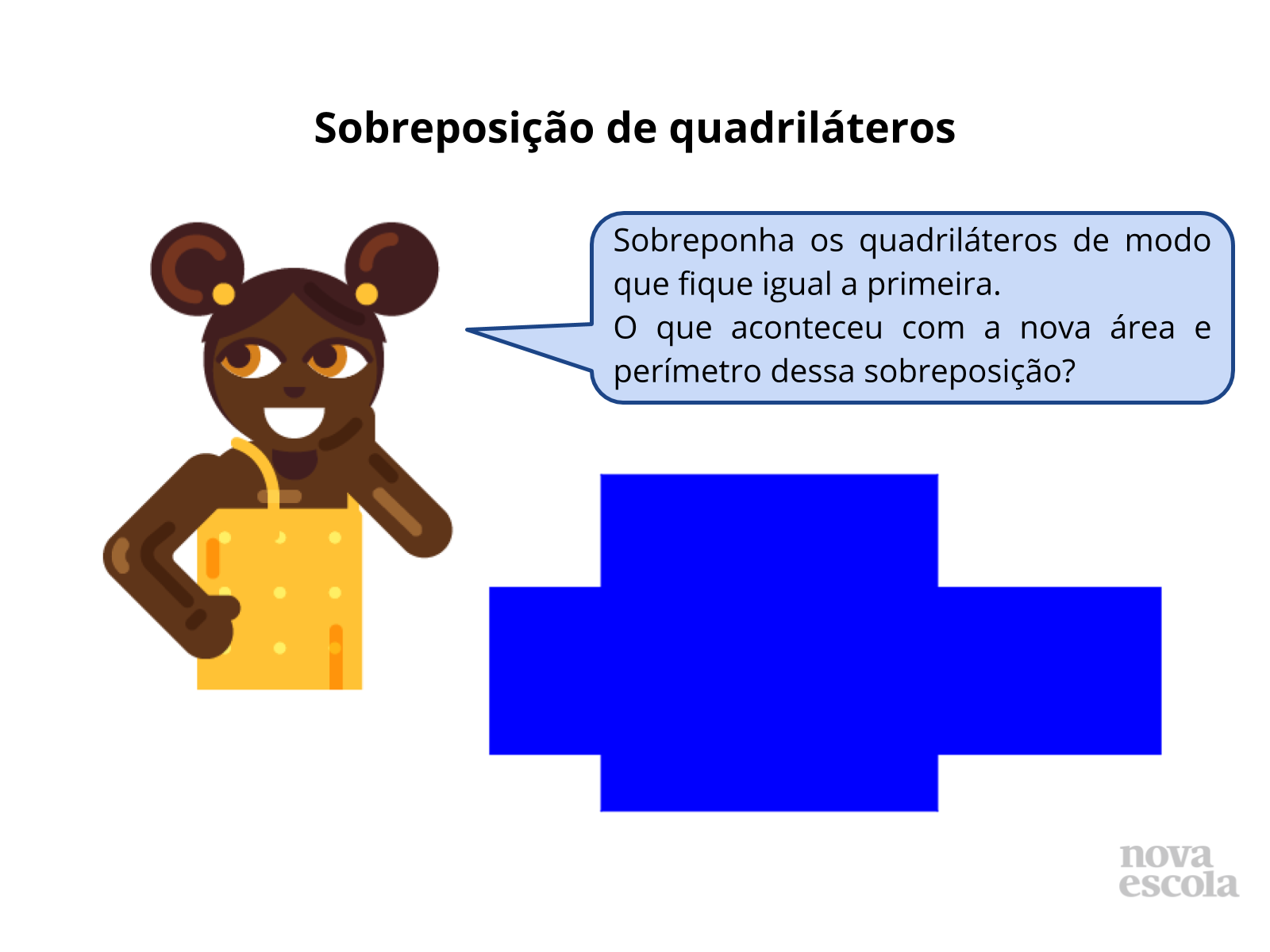
Tempo sugerido: 15 minutos
Orientação: Na mesma folha milimetrada peça para que construam duas figuras ampliadas pelo fator 2
Propósito: Constatar que área do quadrado ou retângulo não é proporcional ao seu lado.
Discuta com a turma:
- O perímetro do retângulo é proporcional ao seu lado? Sim, o perímetro é ampliado ou reduzido pelo mesmo fator ampliou ou reduziu os lados do mesmo.
- A área do retângulo é proporcional ao seu lado? Não, observa-se que não há um fator constante de proporcionalidade entre o lado e área.
- É possível generalizar a área de um retângulo estabelecendo uma correspondência com o fator de ampliação ou redução? Sim, do mesmo modo observado nas tabelas criadas para o quadrado (slides 10 e 11)
Sobreposição de quadriláteros solução 1 (slides 16 ao 21)
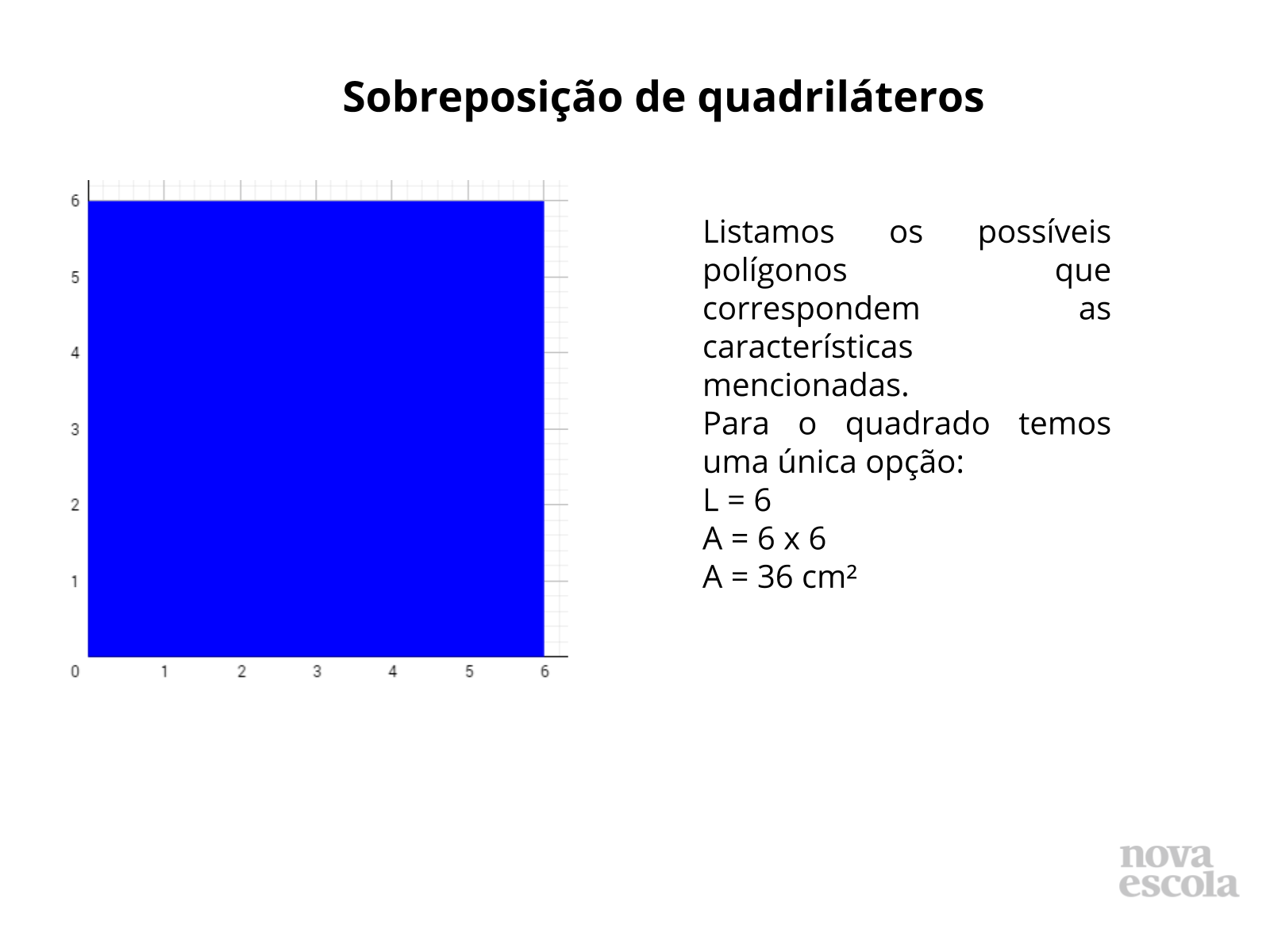
Tempo sugerido: 12 minutos
Orientação: Escolha uma escala para reproduzir o quadrado e o retângulo de área 36 cm² numa cartolina, você pode fixar na lousa ou na parede diversos tipos de sobreposições e pedir para que os alunos façam anotações que julgarem pertinentes nessas figuras.
Propósito: Determinar o lado de quadriláteros sobrepostos a partir da área e do perímetro. Constatar que figuras com perímetros diferentes podem possuir mesma área.
Discuta com a turma:
- Qual outra medida fora dos critérios do exercício poderíamos ter? No caso do quadrado, não é possível representar com outra medida. Você pode reforçar que se trata de um quadrado perfeito, consulte o guia de intervenções aqui. Já para o retângulo podemos ter 30 x 1,2; 8 x 4,5 entre outros.
- Utilizando outros polígonos com mesma área é possível adotar o mesmo padrão? Não, a maneira de determinar a área poderá ser diferente, os segmentos contidos no mesmo plano poderão não ser paralelos.
Sobreposição de quadriláteros solução 1 (slides 16 ao 21)
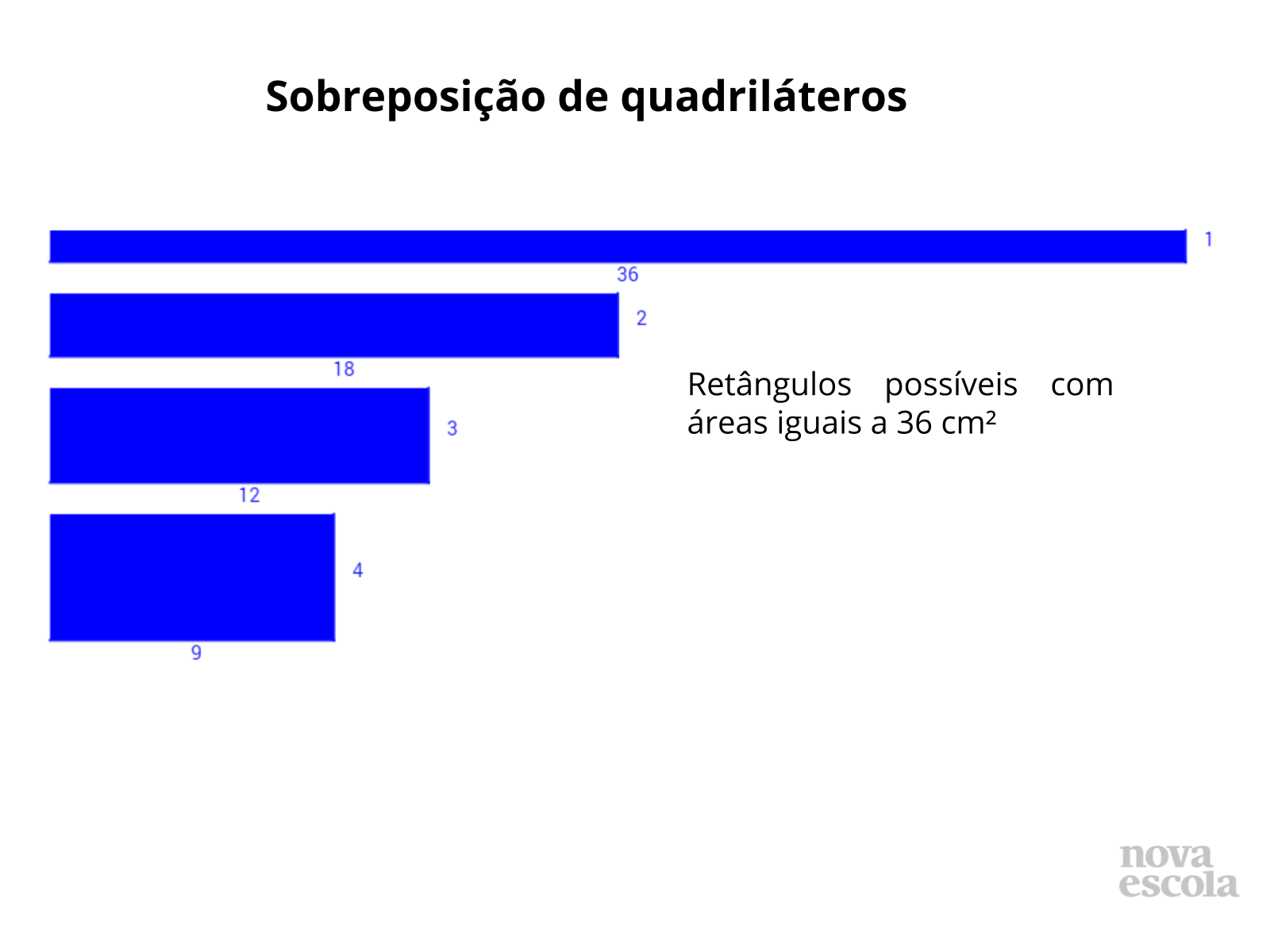
Tempo sugerido: 12 minutos
Orientação: Escolha uma escala para reproduzir o quadrado e o retângulo de área 36 cm² numa cartolina, você pode fixar na lousa ou na parede diversos tipos de sobreposições e pedir para que os alunos façam anotações que julgarem pertinentes nessas figuras.
Propósito: Determinar o lado de quadriláteros sobrepostos a partir da área e do perímetro. Constatar que figuras com perímetros diferentes podem possuir mesma área.
Discuta com a turma:
- Qual outra medida fora dos critérios do exercício poderíamos ter? No caso do quadrado, não é possível representar com outra medida. Você pode reforçar que se trata de um quadrado perfeito, consulte o guia de intervenções aqui. Já para o retângulo podemos ter 30 x 1,2; 8 x 4,5 entre outros.
- Utilizando outros polígonos com mesma área é possível adotar o mesmo padrão? Não, a maneira de determinar a área poderá ser diferente, os segmentos contidos no mesmo plano poderão não ser paralelos.
Sobreposição de quadriláteros solução 1 (slides 16 ao 21)
Tempo sugerido: 12 minutos
Orientação: Escolha uma escala para reproduzir o quadrado e o retângulo de área 36 cm² numa cartolina, você pode fixar na lousa ou na parede diversos tipos de sobreposições e pedir para que os alunos façam anotações que julgarem pertinentes nessas figuras.
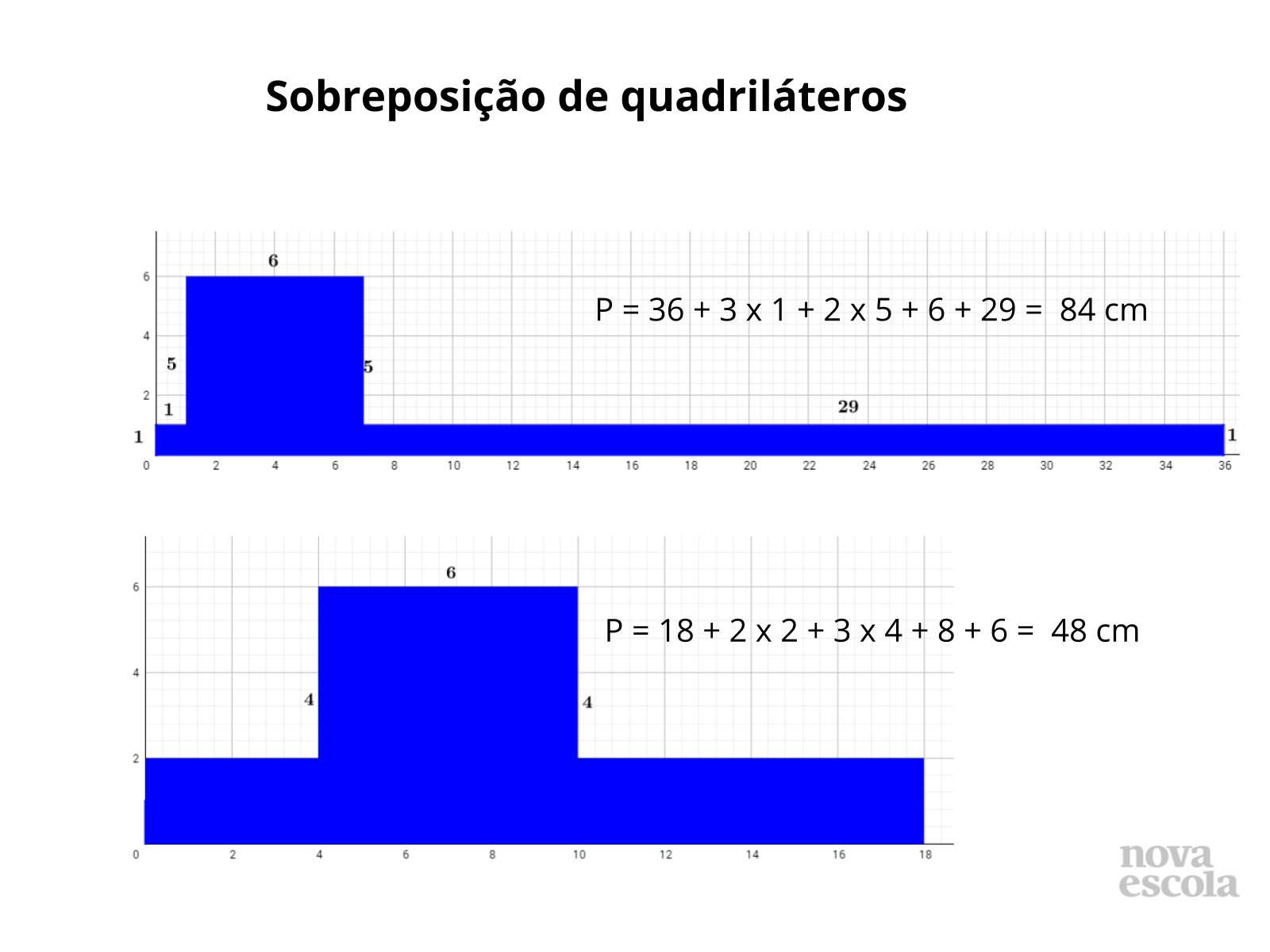
Propósito: Determinar o lado de quadriláteros sobrepostos a partir da área e do perímetro. Constatar que figuras com perímetros diferentes podem possuir mesma área.
Discuta com a turma:
- Qual outra medida fora dos critérios do exercício poderíamos ter? No caso do quadrado, não é possível representar com outra medida. Você pode reforçar que se trata de um quadrado perfeito, consulte o guia de intervenções aqui. Já para o retângulo podemos ter 30 x 1,2; 8 x 4,5 entre outros.
- Utilizando outros polígonos com mesma área é possível adotar o mesmo padrão? Não, a maneira de determinar a área poderá ser diferente, os segmentos contidos no mesmo plano poderão não ser paralelos.
Sobreposição de quadriláteros solução 1 (slides 16 ao 21)
Tempo sugerido: 12 minutos
Orientação: Escolha uma escala para reproduzir o quadrado e o retângulo de área 36 cm² numa cartolina, você pode fixar na lousa ou na parede diversos tipos de sobreposições e pedir para que os alunos façam anotações que julgarem pertinentes nessas figuras.
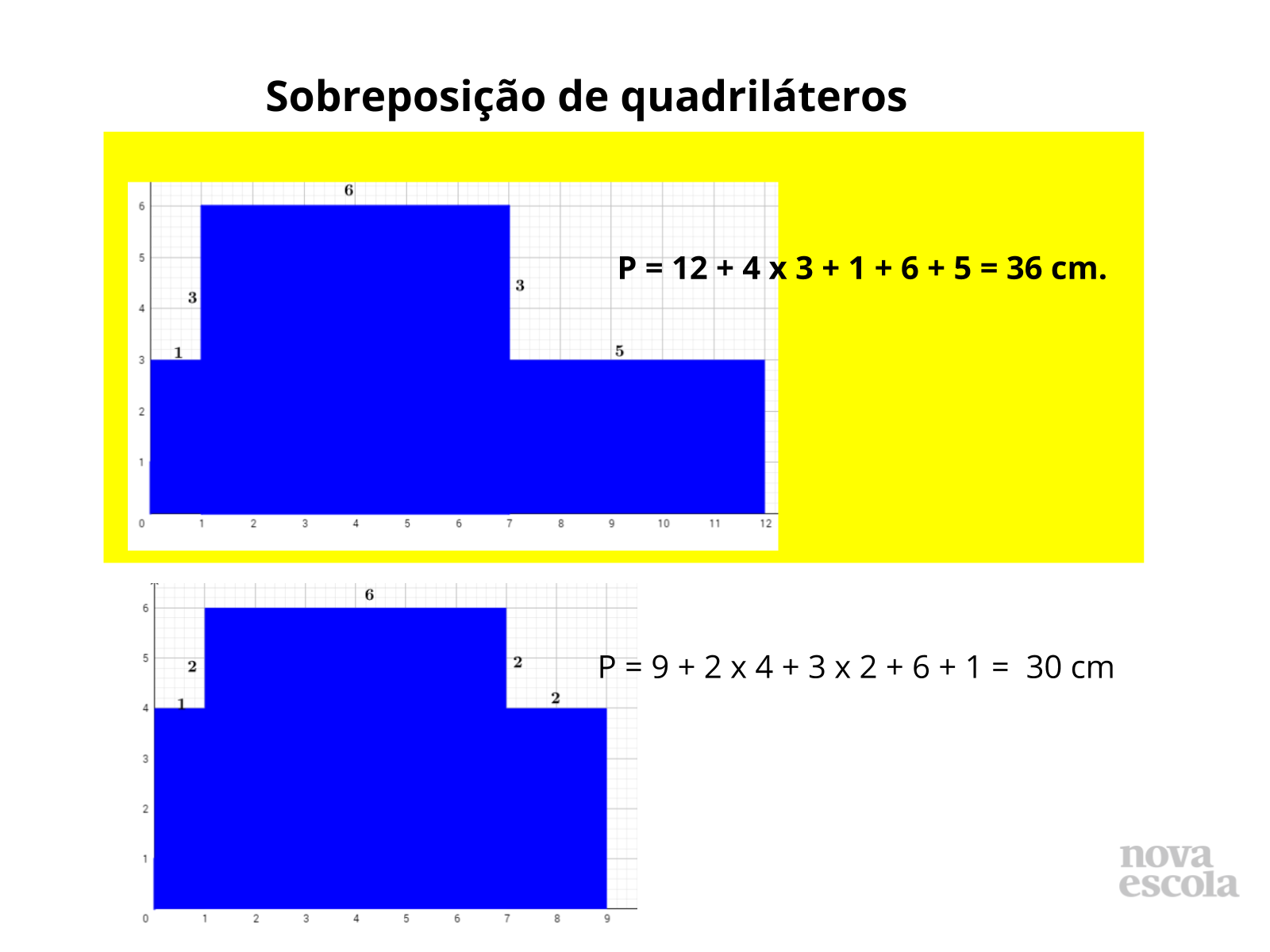
Propósito: Determinar o lado de quadriláteros sobrepostos a partir da área e do perímetro. Constatar que figuras com perímetros diferentes podem possuir mesma área.
Discuta com a turma:
- Qual outra medida fora dos critérios do exercício poderíamos ter? No caso do quadrado, não é possível representar com outra medida. Você pode reforçar que se trata de um quadrado perfeito, consulte o guia de intervenções aqui. Já para o retângulo podemos ter 30 x 1,2; 8 x 4,5 entre outros.
- Utilizando outros polígonos com mesma área é possível adotar o mesmo padrão? Não, a maneira de determinar a área poderá ser diferente, os segmentos contidos no mesmo plano poderão não ser paralelos.
Sobreposição de quadriláteros solução 1 (slides 16 ao 21)
Tempo sugerido: 12 minutos
Orientação: Escolha uma escala para reproduzir o quadrado e o retângulo de área 36 cm² numa cartolina, você pode fixar na lousa ou na parede diversos tipos de sobreposições e pedir para que os alunos façam anotações que julgarem pertinentes nessas figuras.
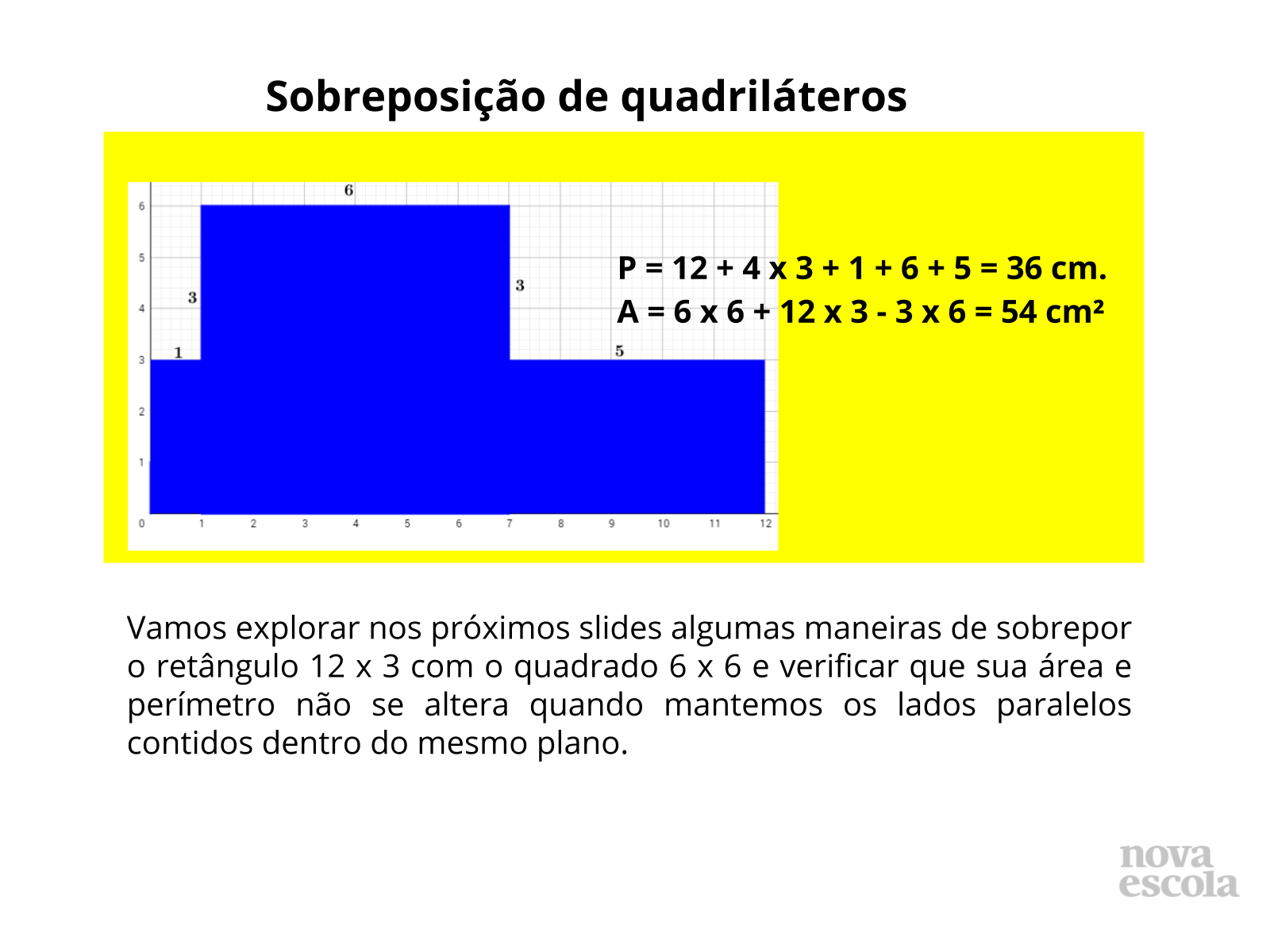
Propósito: Determinar o lado de quadriláteros sobrepostos a partir da área e do perímetro. Constatar que figuras com perímetros diferentes podem possuir mesma área.
Discuta com a turma:
- Qual outra medida fora dos critérios do exercício poderíamos ter? No caso do quadrado, não é possível representar com outra medida. Você pode reforçar que se trata de um quadrado perfeito, consulte o guia de intervenções aqui. Já para o retângulo podemos ter 30 x 1,2; 8 x 4,5 entre outros.
- Utilizando outros polígonos com mesma área é possível adotar o mesmo padrão? Não, a maneira de determinar a área poderá ser diferente, os segmentos contidos no mesmo plano poderão não ser paralelos.
Sobreposição de quadriláteros solução 1 (slides 16 ao 21)
Tempo sugerido: 12 minutos
Orientação: Escolha uma escala para reproduzir o quadrado e o retângulo de área 36 cm² numa cartolina, você pode fixar na lousa ou na parede diversos tipos de sobreposições e pedir para que os alunos façam anotações que julgarem pertinentes nessas figuras.
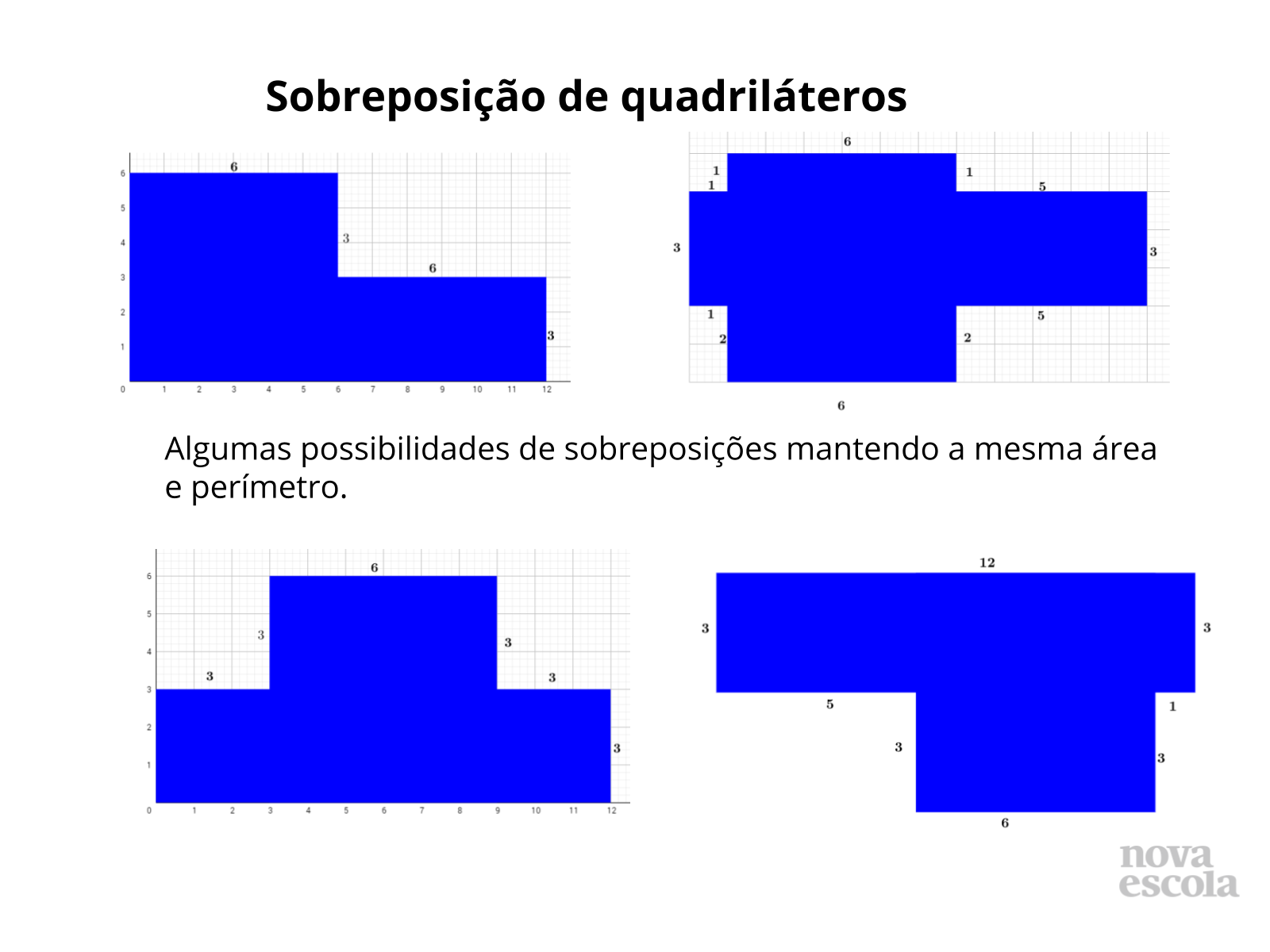
Propósito: Determinar o lado de quadriláteros sobrepostos a partir da área e do perímetro. Constatar que figuras com perímetros diferentes podem possuir mesma área.
Discuta com a turma:
- Qual outra medida fora dos critérios do exercício poderíamos ter? No caso do quadrado, não é possível representar com outra medida. Você pode reforçar que se trata de um quadrado perfeito, consulte o guia de intervenções aqui. Já para o retângulo podemos ter 30 x 1,2; 8 x 4,5 entre outros.
- Utilizando outros polígonos com mesma área é possível adotar o mesmo padrão? Não, a maneira de determinar a área poderá ser diferente, os segmentos contidos no mesmo plano poderão não ser paralelos.
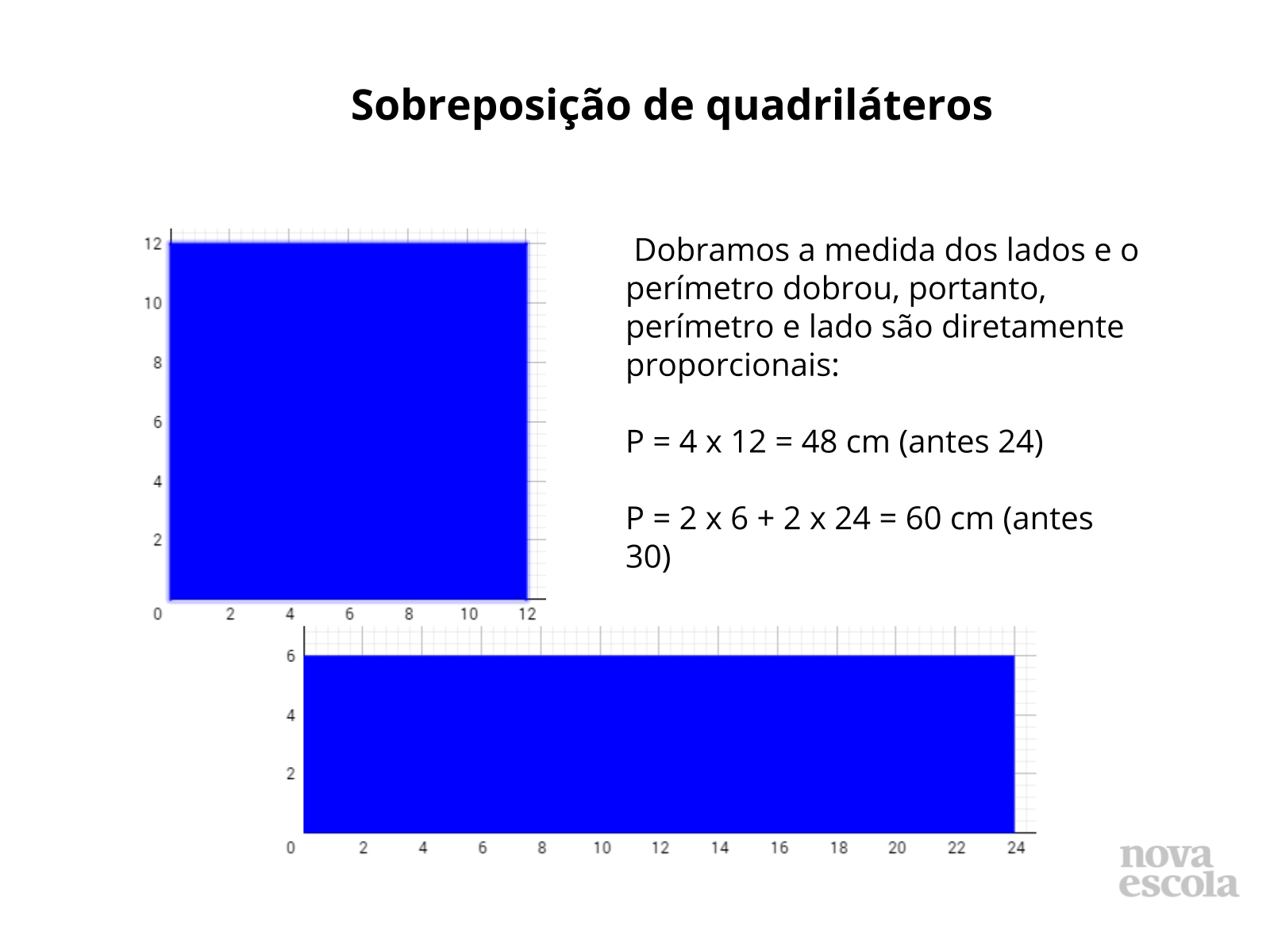
Sobreposição de quadriláteros solução 2 (slides 22 ao 23)
Tempo sugerido: 12 minutos
Orientação: Escolha uma escala para reproduzir o quadrado e o retângulo de área 36 cm² numa cartolina, você pode fixar na lousa ou na parede diversos tipos de sobreposições e pedir para que os alunos façam anotações que julgarem pertinentes nessas figuras.
Propósito: Constatar que figuras com perímetros diferentes podem possuir mesma área e a não proporcionalidade entre lado e área de ambas.
Discuta com a turma:
- Quando se amplia ou reduz os lados das figuras por um mesmo valor, o que acontece com a área da interseção? Segue o mesmo padrão descrito na tabela por exemplo. A área de interseção da figura original corresponde a 18 cm², duplicamos os lados das figuras, ou seja, ampliamos por um fator igual a 2. A nova área de interseção corresponde a 72 cm² que pode ser escrito como fator de ampliação (2) ao quadrado multiplicado pela área original (18) ou como chamamos na tabela de A1 :
2² x 18 ou 2² x A1.
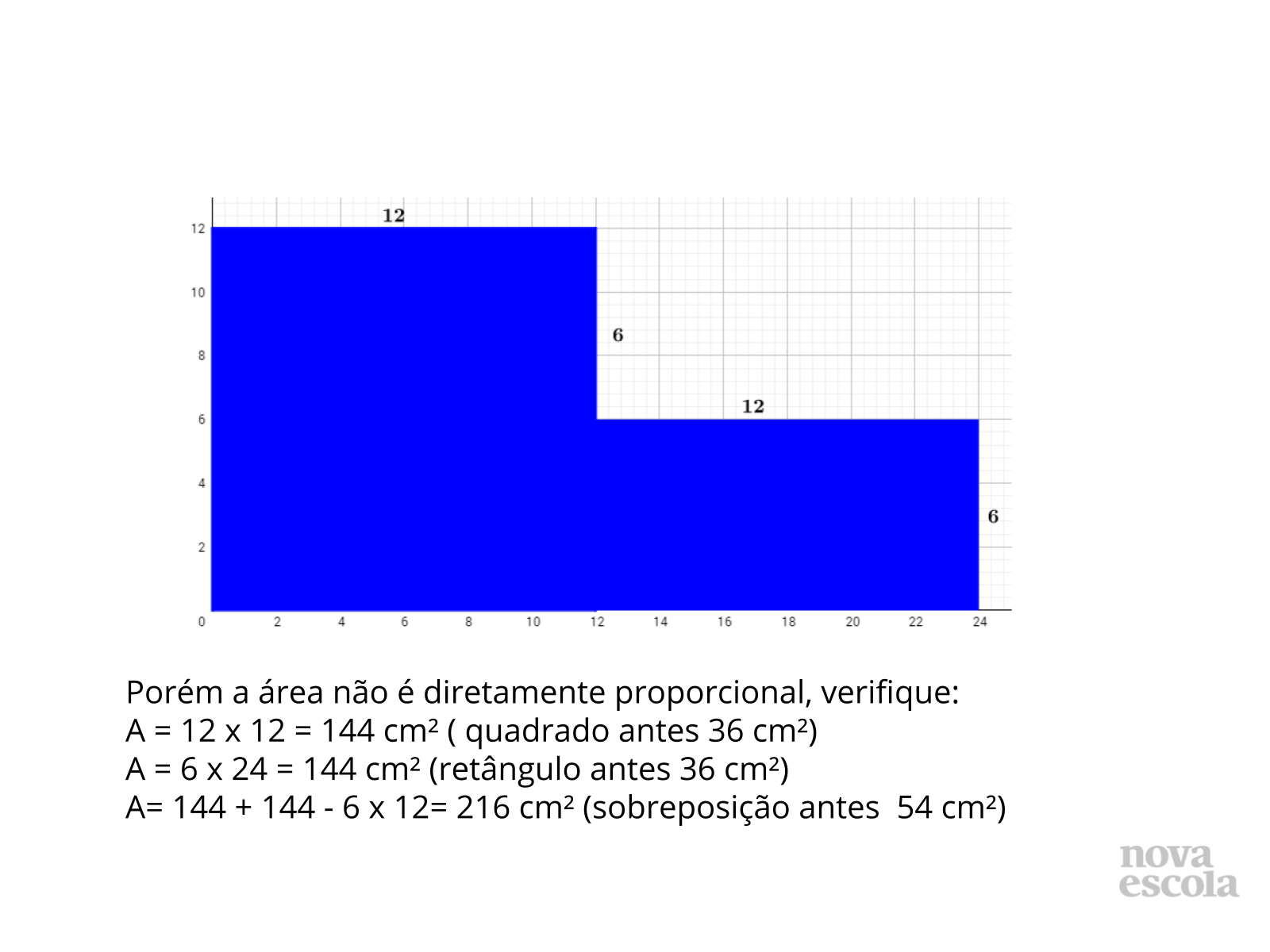
Sobreposição de quadriláteros solução 2 (slides 22 ao 23)
Tempo sugerido: 12 minutos
Orientação: Escolha uma escala para reproduzir o quadrado e o retângulo de área 36 cm² numa cartolina, você pode fixar na lousa ou na parede diversos tipos de sobreposições e pedir para que os alunos façam anotações que julgarem pertinentes nessas figuras.
Propósito: Constatar que figuras com perímetros diferentes podem possuir mesma área e a não proporcionalidade entre lado e área de ambas.
Discuta com a turma:
- Quando se amplia ou reduz os lados das figuras por um mesmo valor, o que acontece com a área da interseção? Segue o mesmo padrão descrito na tabela por exemplo. A área de interseção da figura original corresponde a 18 cm², duplicamos os lados das figuras, ou seja, ampliamos por um fator igual a 2. A nova área de interseção corresponde a 72 cm² que pode ser escrito como fator de ampliação (2) ao quadrado multiplicado pela área original (18) ou como chamamos na tabela de A1 :
2² x 18 ou 2² x A1.
Sistematização de Conceito

Tempo sugerido: 2 minutos.
Orientação: Leia com os alunos e verifique se o conceito de proporcionalidade apenas entre lado e perímetro foi compreendido.
Encerramento
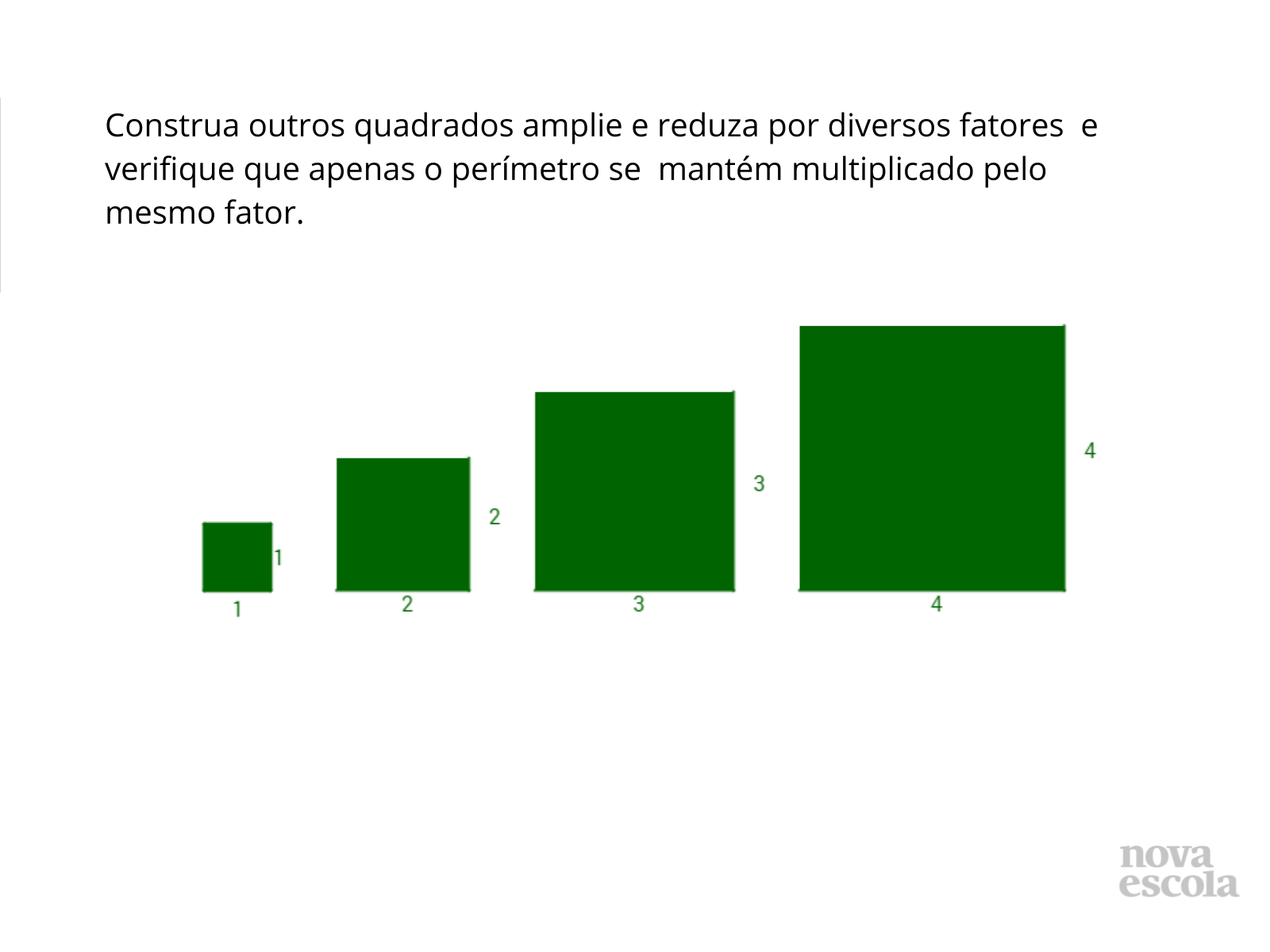
Tempo sugerido: 2 minutos.
Orientação: Determine as áreas e perímetros dos diversos quadrados com os alunos, apontando a proporcionalidade existente entre lado e perímetro.
Raio X: Ampliando uma caixa cúbica
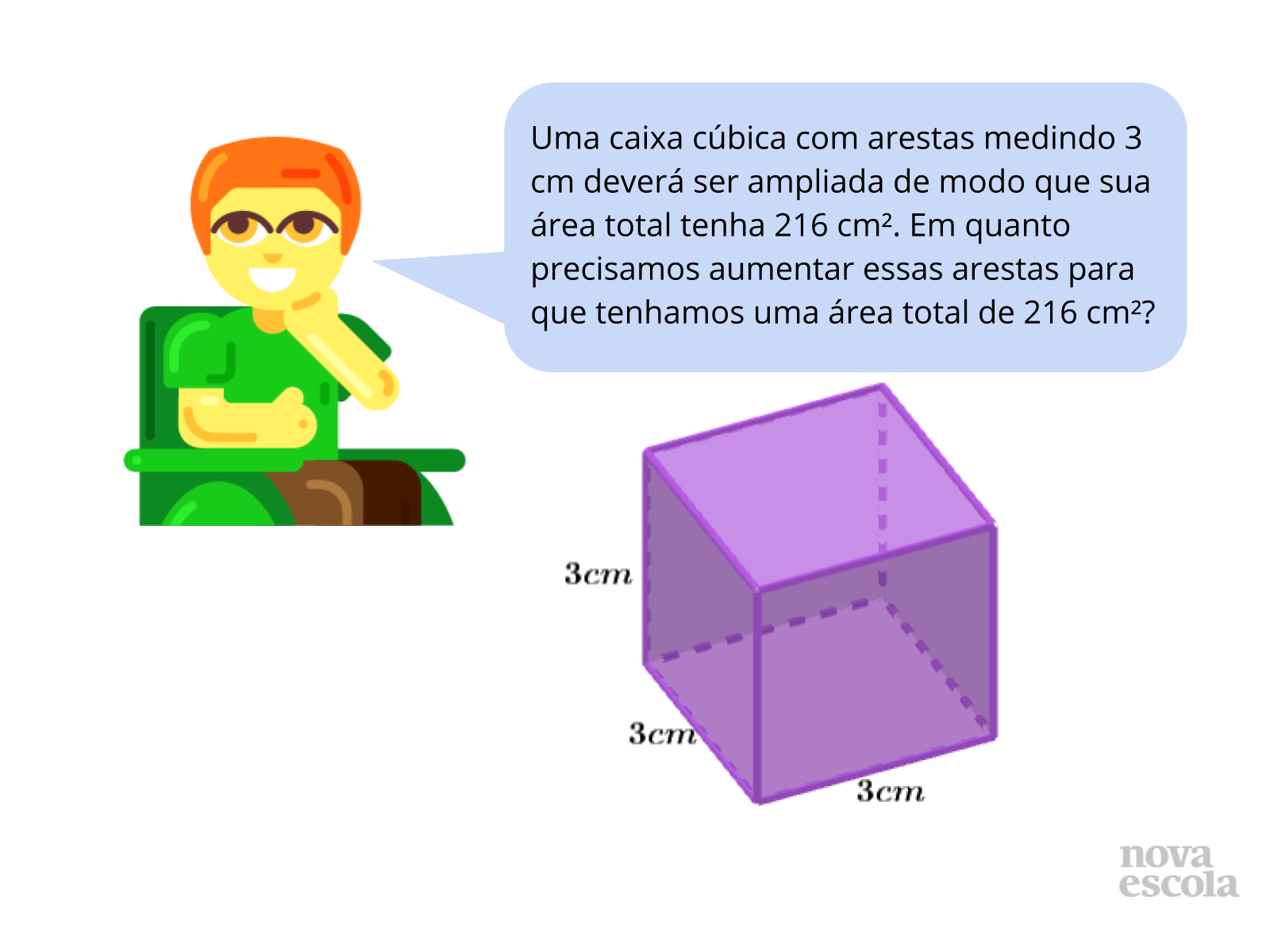
Tempo sugerido: 9 minutos
Orientação: Leia o enunciado com os alunos , você pode utilizar uma caixa cúbica, cubo mágico para e deixá-lo a mostra para que os alunos manipulem se acharem necessário
Propósito: Determinar a nova aresta de um cubo ampliado a partir de sua área total.
Discuta com a turma:
- Existe alguma relação entre a medida da aresta com a soma das medidas de todas as arestas do cubo? Sim, elas são diretamente proporcionais, logo aumentam e diminuem a mesma medida.
- Quando aumentamos as arestas do cubo aumentamos seu volume também. Analisando o aumento da aresta, da área e do volume, existe alguma relação entre elas? Quando aumentamos ou diminuímos a aresta de um cubo por um fator k, a área total será dada pelo produto do fator ao quadrado e área que será ampliada enquanto seu volume será dado por pelo produto do fator ao cubo e volume que será ampliado.
Materiais complementares para impressão:
Anexo da atividade complementar
Sugestão de adaptação para ensino remoto
Código do plano
MAT6_22GRM01
Recursos
- Necessários: Caderno, lápis, régua, tesoura, folha milimetrada
- Opcionais: Zoom, Meet
Testando área e perímetro: https://www.youtube.com/watch?v=7vyh1i2FNU8
Para este plano foque na etapa Aquecimento
Aquecimento
Nessa aula é importante o uso dos materiais indicados. Para isso, compartilhe com antecedência com os alunos os slides (3 ao 7) pelo WhatsApp ou outro meio de comunicação combinado com eles. Grave um áudio orientativo. O Aquecimento será o cerne da sua aula. Sugira que todos os alunos façam a atividade em casa e mantenha um canal de comunicação para dúvidas e esclarecimentos. Na construção e análise das atividades os alunos precisam focar em alguns pontos:
- Como podemos garantir que os novos quadriláteros formados pelos recortes são quadrados?
- O que acontece com área de um quadrado quando ampliamos ou reduzimos seus lados?
- O que acontece com o perímetro de um quadrado quando ampliamos ou reduzimos seus lados?
- Existe alguma relação de proporcionalidade entre os lados e o perímetro?
- Existe alguma relação de proporcionalidade entre os lados e área?
Ao final da vivência peça aos alunos que assistam ao vídeo https://www.youtube.com/watch?v=7vyh1i2FNU8.
Se sua aula fora assíncrona você pode deixar a atividade impressa na escola ou enviar pelo grupo de WhatsApp e combinar um retorno com eles para uma devolutiva. Nesse retorno, você pode enviar um áudio, registros de outros alunos para que eles comparem com suas estratégias e colem no seu caderno como repertório de soluções.
Discussão das soluções
Avalie as respostas e dúvidas apresentadas pelos alunos para dar um feedback à turma. Se sua aula for síncrona, abra o áudio e ouça as hipóteses ou dúvidas vivenciadas por eles. Volte as perguntas iniciais. Garanta que eles chegaram as conclusões quanto a proporcionalidade o que acontece com a área e perímetro do quadrado. Questione: O que acontece quando ampliamos ou reduzimos o quadrado? A área e/ou o perímetro permanece o mesmo? Se sim, justifique. Que tipo de generalização podemos realizar com os resultados obtidos? Deixe preparado uma tabela (como exemplo) com possíveis lados e áreas para que eles façam comparações e cheguem a conclusões. Façam boas perguntas e deixem que eles compartilhem o que fizeram. O vídeo será de boa ajuda par ao entendimento. Prepare um áudio com explicação para um fechamento da aula.
Use o encerramento como atividade complementar ou tarefa de casa.
Convite às famílias
A participação das famílias no processo de aprendizagem é de grande importância para o aluno. Porém, ressaltamos que os pais não são professores de matemática e muitos estão ocupados nessa fase com outras funções em casa. Peça às famílias, que oportunamente, auxiliem na leitura das comandas e no envio das soluções, conforme os combinados com o professor. É importante que as famílias acompanhem as atividades nos canais de comunicação estabelecidos entre vocês.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Elizabeth Bento
Mentor: Maria Aparecida Nemet Nascimento
Especialista de área: Fernando Barnabé
Habilidade da BNCC
(EF06MA27) Analisar e descrever as mudanças que ocorrem no perímetro e área de um quadrado quando ampliamos ou reduzimos seus lados por um fator k.
Habilidades necessárias
Determinar perímetro e área de um quadrilátero, reconhecer quando há proporcionalidade entre duas grandezas, compreender entes da geometria como ponto médio, diagonal e vértice.
Objetivos específicos
Concluir que apenas lado e perímetro de um quadrado são proporcionais.
Conceito-chave
Área, perímetro, proporcionalidade.
Recursos necessários
- Folha milimetrada;
- Lápis de cor;
- Tesoura;
- Transferidor;
- Régua.