Aquecimento
Plano de Aula
Plano de aula: Situações problema
Plano 4 de uma sequência de 10 planos. Veja todos os planos sobre Resolução de problemas
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Érica Fernanda Barbosa dos Santos.
Mentor: Tatiane Cristina Guadagnucci.
Especialista de área: Rita Batista.
Habilidade da BNCC
NÃO HÁ.
Objetivos específicos
Resolver e elaborar problemas que envolvam cálculos mentais ou escritos com números naturais, por meio de estratégias variadas, com compreensão dos processos neles envolvidos com e sem uso de calculadora.
Conceito-chave
Investigar diferentes soluções para situações problemas.
Recursos necessários
- Folha de papel A4 branca;
- Atividades impressas em folhas, coladas no caderno ou não.
Habilidades BNCC:
Objetivos de aprendizagem
Resolver e elaborar problemas que envolvam cálculos mentais ou escritos com números naturais, por meio de estratégias variadas, com compreensão dos processos neles envolvidos com e sem uso de calculadora.
Resumo da aula
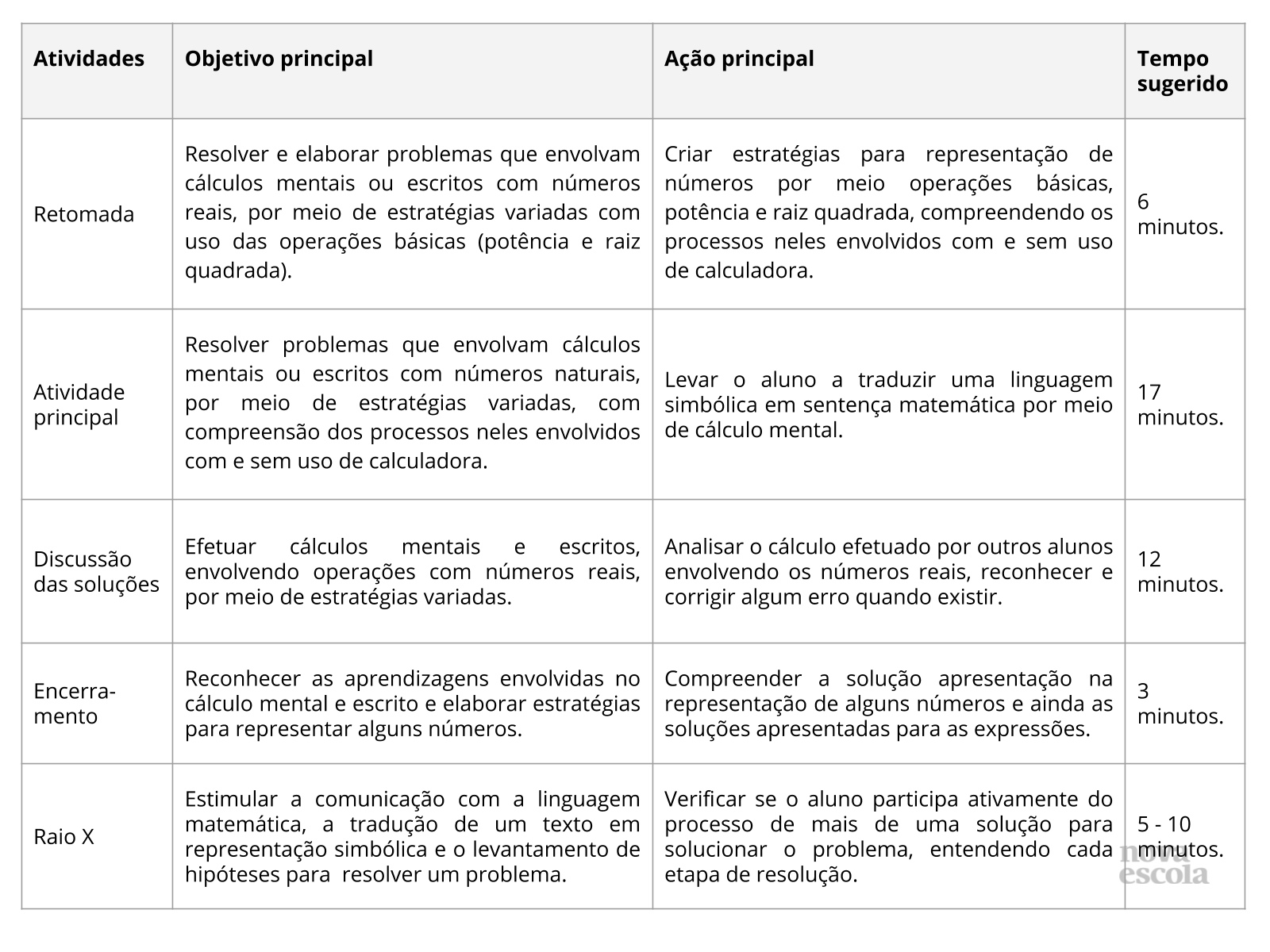 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na parte “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Apresente o objetivo para a turma. Você pode projetar ou escrever na lousa.
Propósito: Compartilhar o objetivo da aula para que os alunos saibam o que professor pretende desenvolver na aula.
Retomada

Tempo sugerido: 17 minutos.
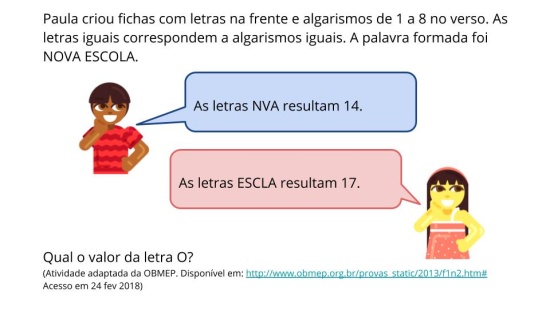
Orientação: Leia a pergunta aos alunos e divida a sala em grupos com quatro alunos em cada. Estimule-os a propor algumas possíveis representações para solucionar o problema. Aguarde 6 minutos para que alunos discutam e registrem a resposta. Solicite o registro da solução no caderno. Não faça nenhuma intervenção neste momento, observe como os alunos analisam os dados do problema, interpretam e elaboram suas estratégias. Em seguida, promova um debate coletivo e deixe que o quarteto compartilhe o que discutiram.
Essa atividade pode ser aplicada por meio de um jogo. Para tanto, segue proposta:
“Quais são as expressões que resultam 99?” Você pode considerar todo conjunto dos reais, adição, subtração, multiplicação, divisão, potência e raiz.
Projete a atividade ou escreva na lousa. Entregue uma folha sulfite com identificação para cada grupo, para registrar as possíveis expressões. Em seguida entregue um cartão no qual deve constar uma tabela para indicar a pontuação de cada grupo. Vence o grupo que fizer a maior pontuação. Após criadas as expressões os grupos podem trocar seus cartões para fazer correção e verificar a pontuação. Por exemplo, o grupo A entrega seu cartão de solução para o grupo B fazer a correção, e vice-versa. Essa troca se repete com os demais. Em seguida o professor recolhe a ficha de todos os grupos para conferir a pontuação. Sugiro que seja disponibilizado 6 minutos para criar as expressões.
Utilize o guia de intervenções para discutir com os alunos as formas e possibilidades de representar a solução.
Propósito: Fazer com que os alunos mobilizem os conhecimentos que já possuem diante das operações básicas para representar um número.
Discuta com a turma:
- O que é representação matemática?
- O número 99 pode ser representado por meio de adição, subtração, multiplicação, divisão, potência, raiz quadrada?
- A representação pode ser por meio de expressão numérica? Quais operações podem ser utilizada nas expressões?
Materiais complementares para impressão:
Retomada
Tempo sugerido: 17 minutos.
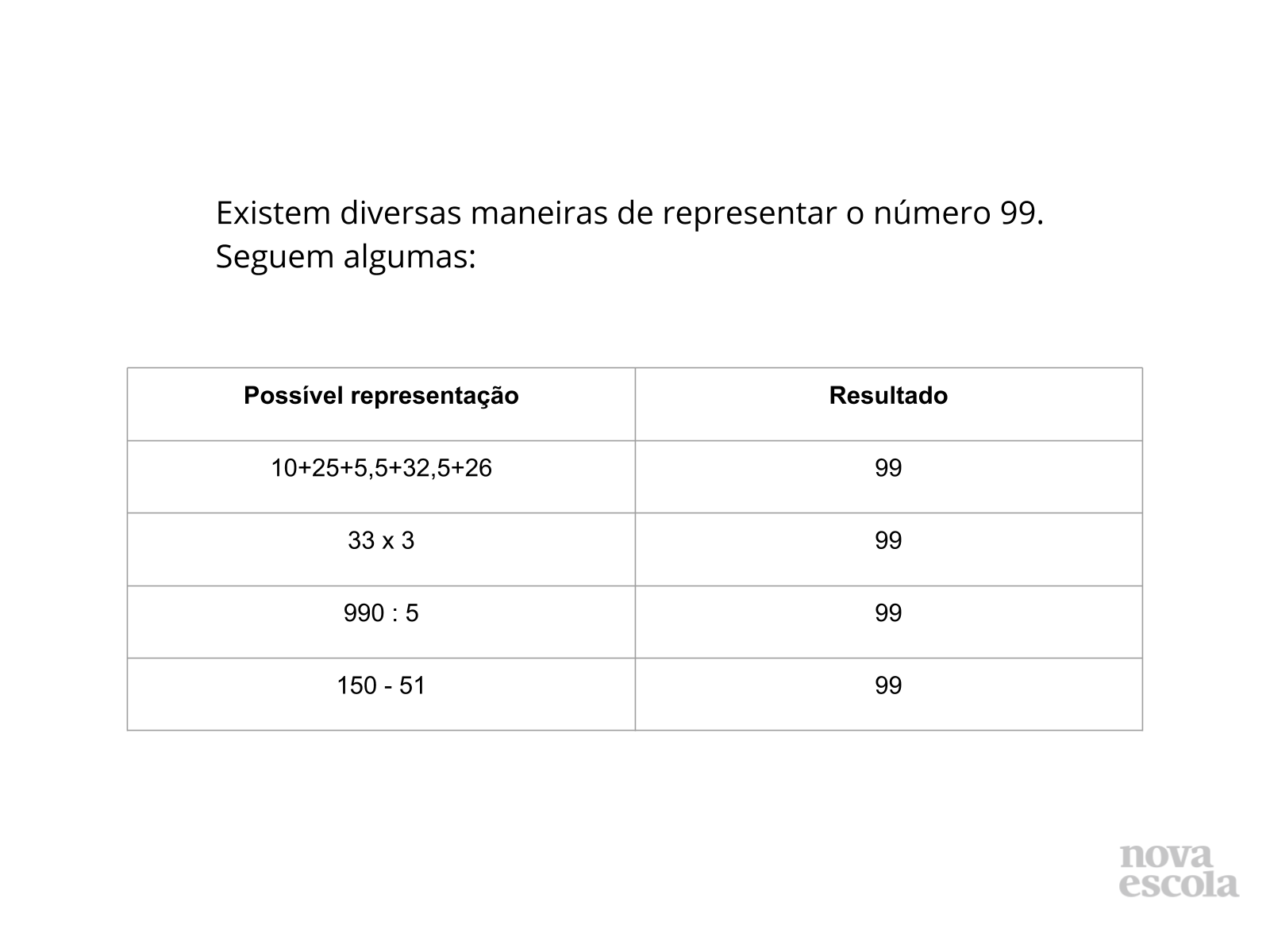
Orientação: Peça para os grupos de alunos compararem suas respostas. Neste slide segue uma sugestão de solução, e se nenhum aluno representar uma solução parecida apresente-a para o grupo para que os alunos percebam que podem representar o número 99 por meio de várias operações e também por expressão numérica.
Propósito: Promover a interação na investigação e sugestão de hipóteses para solucionar um problema.
Discuta com a turma:
- Será possível representar o número 99 por meio de raiz cúbica? (Sim, a raiz cúbica de 970 299 resulta em 99).
- O número 99 pode ser representado por meio de potência? (Sim, da seguinte maneira: 3².11).
- Posso representar o número 99 por meio de produtos notáveis? Se ainda não ensinou produtos notáveis para sua turma não discuta esta pergunta. (Sim, por meio do quadrado da soma pela diferença de dois termos: 10²-1².
Atividade Principal

Tempo sugerido: 17 minutos (Slides 5 e 6).
Orientação: Projete ou escreva a atividade na lousa, peça para os alunos individualmente descobrirem o valor da incógnita.
Propósito: Estimular a interpretação de uma situação problema e fazer a representação matemática para encontrar a solução.
Discuta com a turma:
- Ao observar D²=9, você pensa em qual número que ao ser multiplicado por ele mesmo resulta em 9? (Logo descobrimos que D=3). É importante ressaltar que D também pode assumir o valor D= -3.
- Ao descobrir o valor de D=3, é possível descobrir o valor de P? (sim, pois, D+P=D, logo: 3+0=3).
- Sabendo que D=3, é possível descobrir o valor de X? (Sendo X:D=160, então X:3=160, logo 160.3=480. Portanto X=480).
- Sabendo que X=480, e Y+X=630, qual o valor de y? (Para descobrir o valor de Y basta subtrair 480 de 630. Portanto Y=150)
- Sabendo que y=150, qual o valor de T?
- Sabendo que X=480, é possível descobrir o valor de R? (Sendo 7000-X=R, então 7000-480=6520)
Materiais complementares para impressão:
Atividade principal - fichas de jogo
Atividade principal - cartão de pontos
Atividade Principal
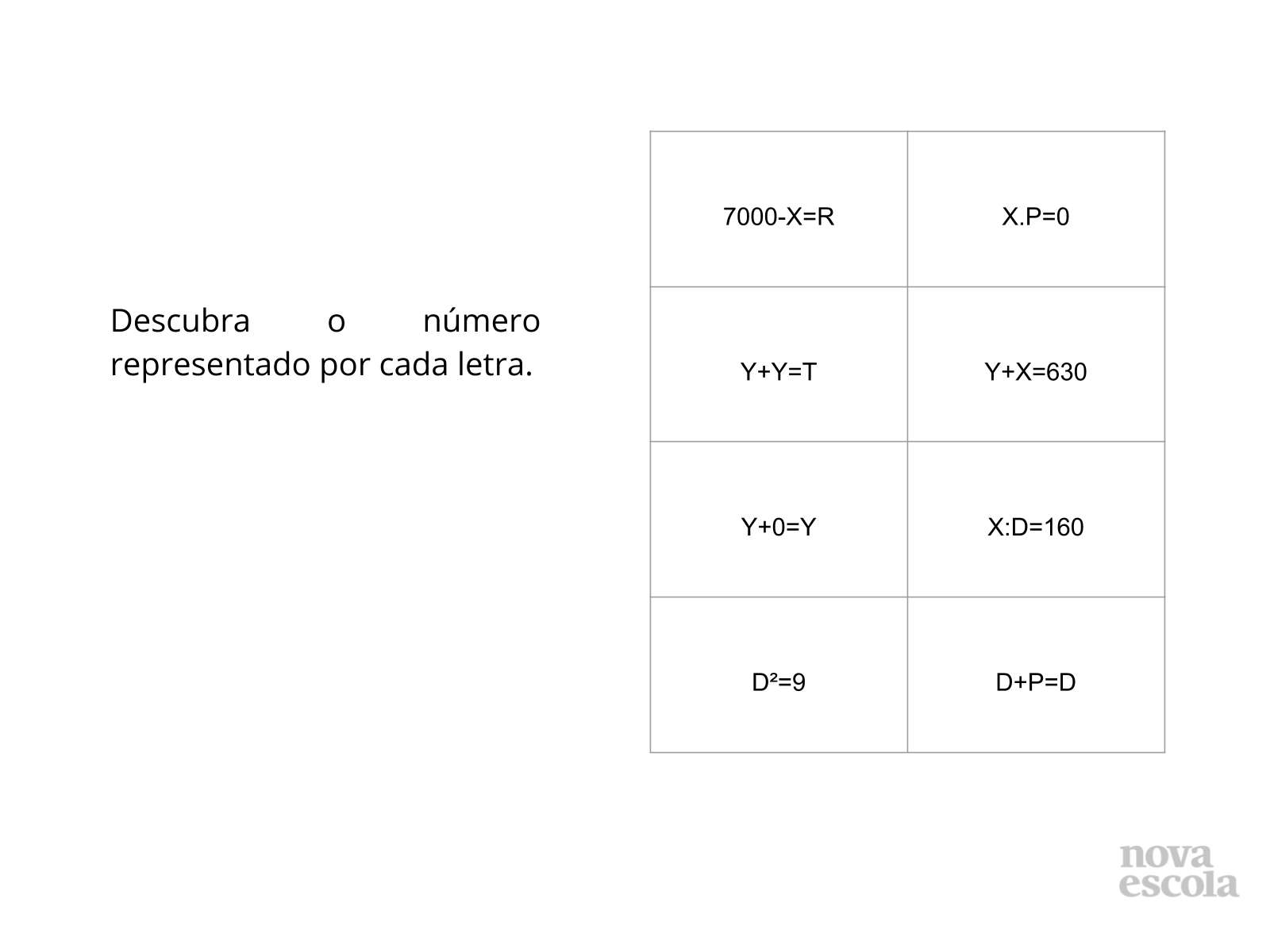
Tempo sugerido: 17 minutos (Slides 5 e 6).
Orientação: Projete ou escreva a atividade na lousa, peça para os alunos individualmente descobrirem o valor da incógnita. Professor é importante que o aluno perceba que os resultados se alteram quando o sinal se altera, é importante que façam a resolução utilizando D=3 e D= -3.
Propósito: Estimular a interpretação de uma situação problema e fazer a representação matemática para encontrar a solução.
Discuta com a turma:
- Ao observar D²=9, você pensa em qual número que ao ser multiplicado por ele mesmo resulta em 9? (Logo descobrimos que D=3). É importante ressaltar que D também pode assumir o valor D= -3.
- Ao descobrir o valor de D=3, é possível descobrir o valor de P? (sim, pois, D+P=D, logo: 3+0=3).
- Sabendo que D=3, é possível descobrir o valor de X? (Sendo X:D=160, então X:3=160, logo 160.3=480. Portanto X=480).
- Sabendo que X=480, e Y+X=630, qual o valor de y? (Para descobrir o valor de Y basta subtrair 480 de 630. Portanto Y=150)
- Sabendo que y=150, qual o valor de T?
- Sabendo que X=480, é possível descobrir o valor de R? (Sendo 7000-X=R, então 7000-480=6520)
Discussão da solução
Tempo sugerido: 12 minutos (Slides 7 e 8).
Orientação: Projete ou escreva a atividade na lousa, peça para os alunos individualmente descobrirem o valor da incógnita.
Propósito: Estimular a interpretação de uma situação problema e fazer a representação matemática para encontrar a solução.
Discuta com a turma:
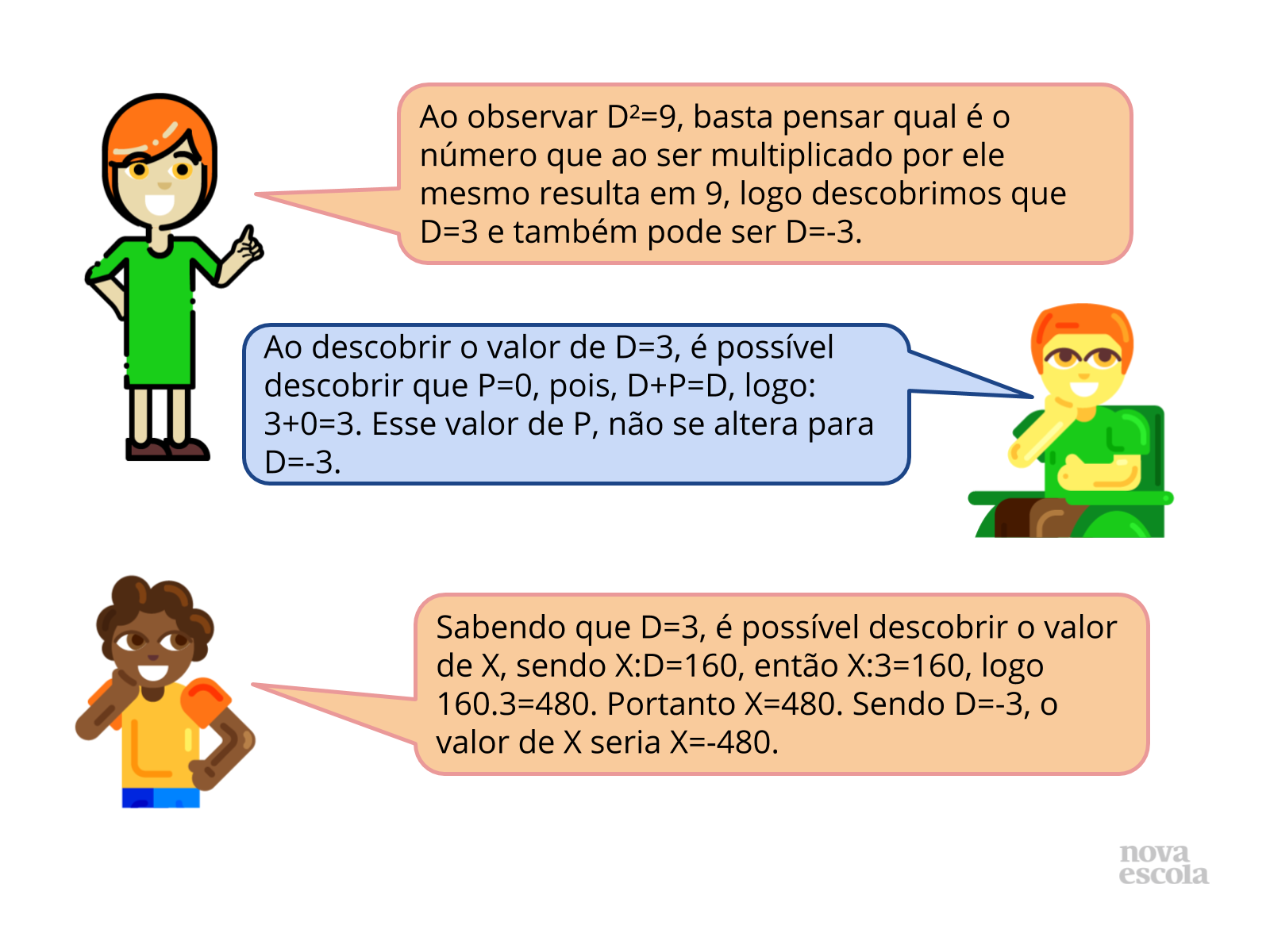
- Ao observar D²=9, você pensa em qual número que ao ser multiplicado por ele mesmo resulta em 9? (Logo descobrimos que D=3).
- Ao descobrir o valor de D=3, é possível descobrir o valor de P? (sim, pois, D+P=D, logo: 3+0=3).
- Sabendo que D=3, é possível descobrir o valor de X? (Sendo X:D=160, então X:3=160, logo 160.3=480. Portanto X=480).
- Sabendo que X=480, e Y+X=630, qual o valor de y? (Para descobrir o valor de Y basta subtrair 480 de 630. Portanto Y=150)
- Sabendo que y=150, qual o valor de T?
- Sabendo que X=480, é possível descobrir o valor de R? (Sendo 7000-X=R, então 7000-480=6520)
Discussão da solução
Tempo sugerido: 12 minutos (Slides 7 e 8).
Orientação: Projete ou escreva a atividade na lousa, peça para os alunos individualmente descobrirem o valor da incógnita.
Propósito: Estimular a interpretação de uma situação problema e fazer a representação matemática para encontrar a solução.
Discuta com a turma:
- Ao observar D²=9, você pensa em qual número que ao ser multiplicado por ele mesmo resulta em 9? (Logo descobrimos que D= +/-3).
- Ao descobrir o valor de D=3, é possível descobrir o valor de P? (sim, pois, D+P=D, logo: 3+0=3).
- Sabendo que D=3, é possível descobrir o valor de X? (Sendo X:D=160, então X:3=160, logo 160.3=480. Portanto X=480).
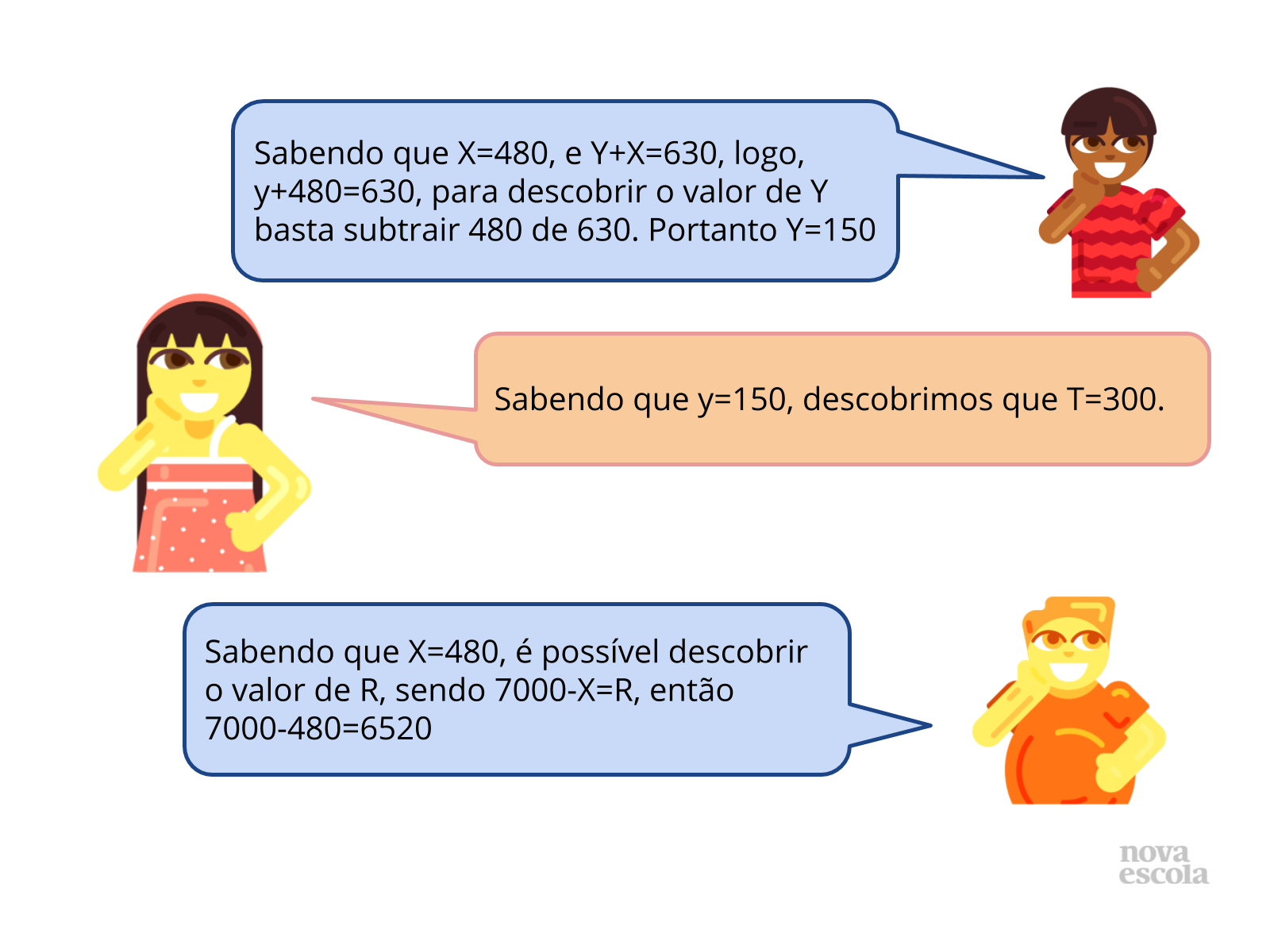
- Sabendo que X=480, e Y+X=630, qual o valor de y? (Para descobrir o valor de Y basta subtrair 480 de 630. Portanto Y=150)
- Sabendo que y=150, qual o valor de T?
- Sabendo que X=480, é possível descobrir o valor de R? (Sendo 7000-X=R, então 7000-480=6520)
Discussão da solução
Tempo sugerido: 12 minutos (Slides 7 e 8).
Orientação: Projete ou escreva a atividade na lousa, peça para os alunos individualmente descobrirem o valor da incógnita.
Propósito: Estimular a interpretação de uma situação problema e fazer a representação matemática para encontrar a solução.
Discuta com a turma:
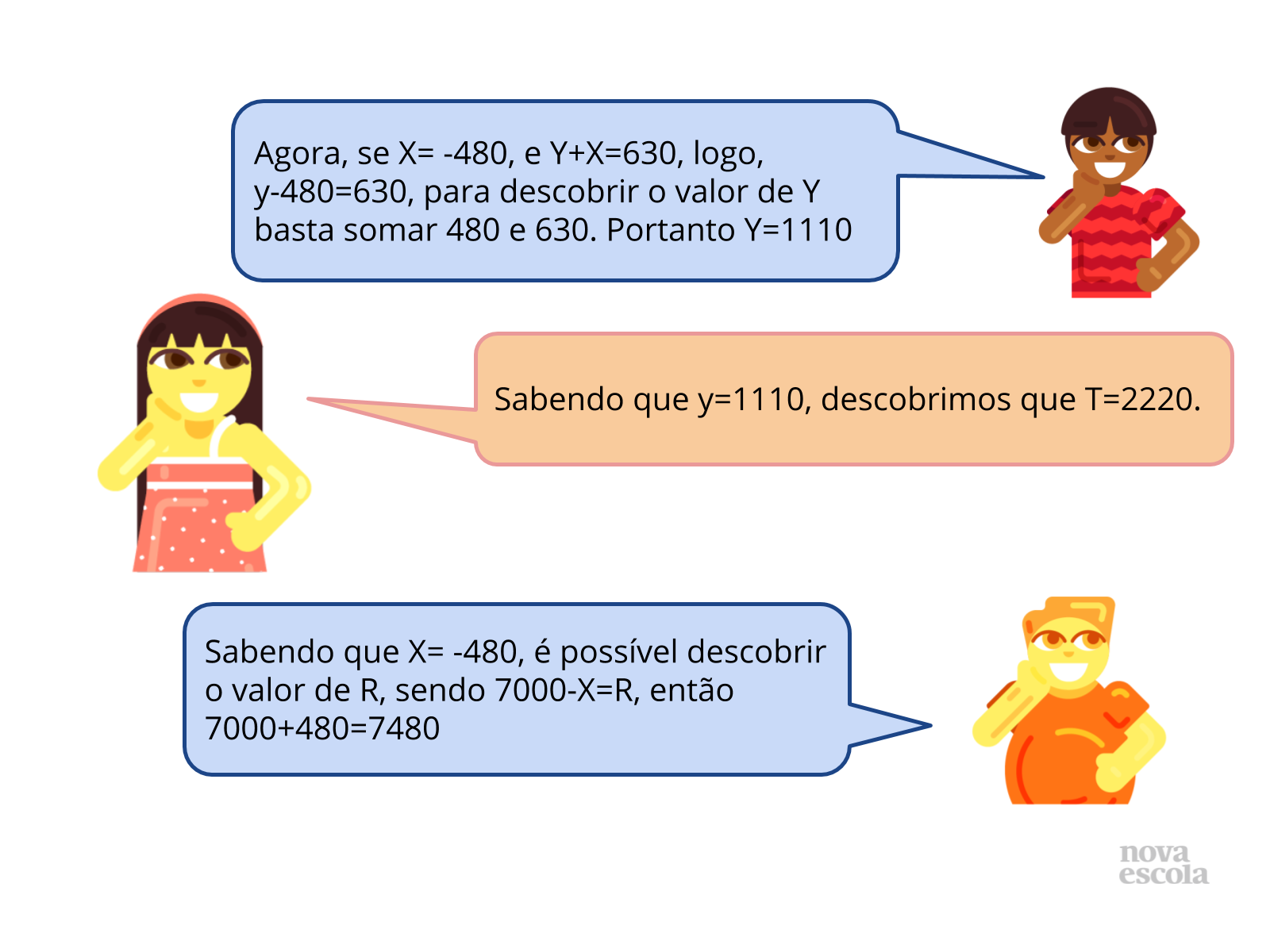
- Ao observar D²=9, você pensa em qual número que ao ser multiplicado por ele mesmo resulta em 9? (Logo descobrimos que D= +/-3).
- Ao descobrir o valor de D=3, é possível descobrir o valor de P? (sim, pois, D+P=D, logo: 3+0=3).
- Sabendo que D=3, é possível descobrir o valor de X? (Sendo X:D=160, então X:3=160, logo 160.3=480. Portanto X=480).
- Sabendo que X=480, e Y+X=630, qual o valor de y? (Para descobrir o valor de Y basta subtrair 480 de 630. Portanto Y=150)
- Sabendo que y=150, qual o valor de T?
- Sabendo que X=480, é possível descobrir o valor de R? (Sendo 7000-X=R, então 7000-480=6520)
Encerramento
Tempo sugerido: 3 minutos.
Orientação: Encerre a atividade retomando com os alunos as diversas maneiras de representar um número real por meio das operações básicas e expressões numéricas, compreendendo cada processo de resolução. Os alunos devem ser estimulados a acreditar que todo problema pode não ter uma única resposta e que o problema que apresenta duas ou mais soluções pode reconhecer todas soluções apresentadas como verdadeiras.
Propósito: Sintetizar o conhecimento adquirido na aula.
Discuta com a turma:
- Como você ou seu grupo abordou o problema ou conjunto de problemas de hoje? Sua abordagem foi bem sucedida? O que você aprendeu com sua abordagem?
- O que se manteve como você pensava? O que mudou?
- O que aconteceria se você mudasse algum aspecto?
Raio X
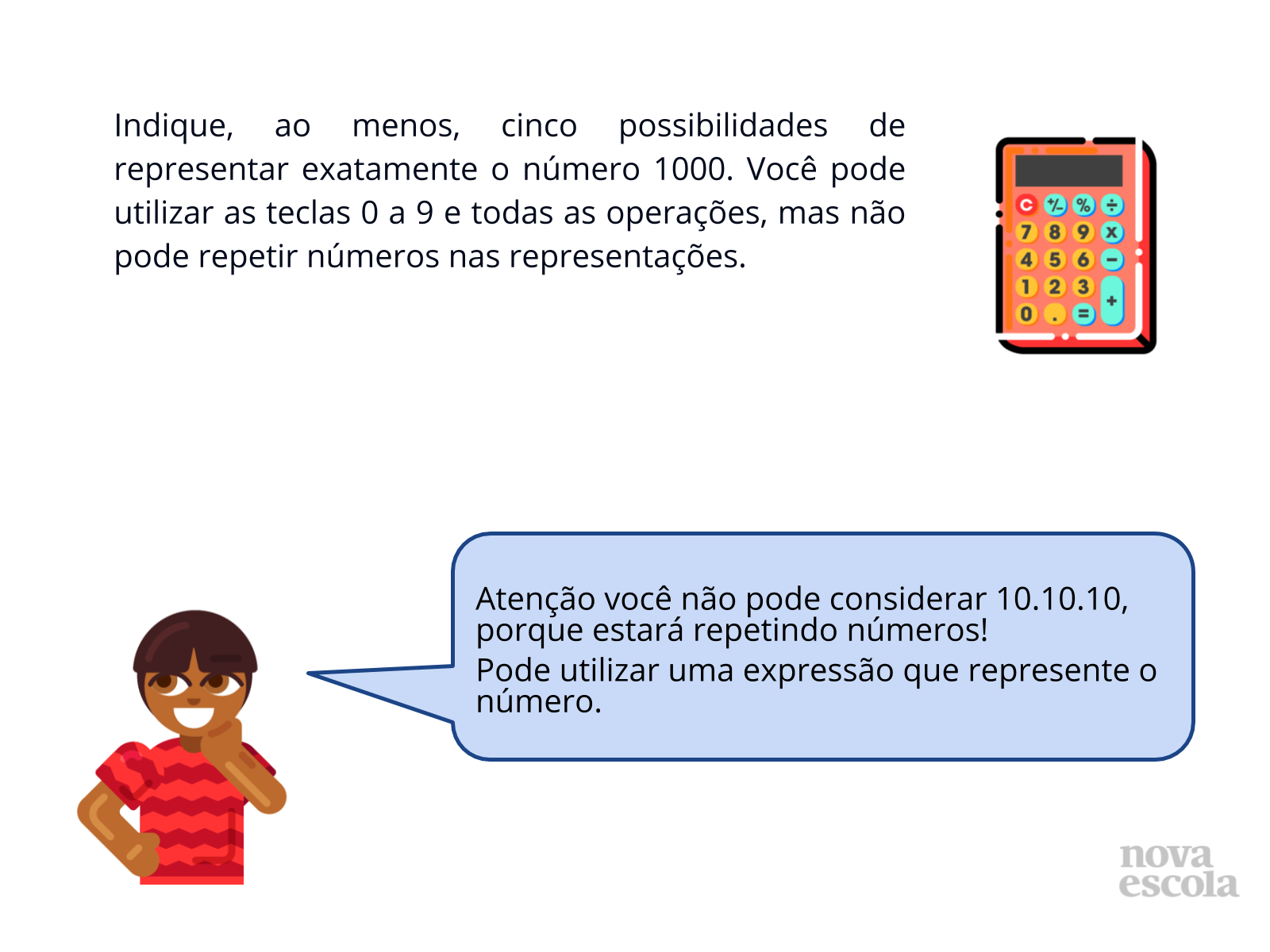
Tempo sugerido: 5 - 10 minutos (Slides 9 a 11).
Orientação: Entregue aos alunos uma cópia da questão, para que individualmente criem estratégias que venham mostrar uma ou mais soluções de uma situação problema. Nesta atividade faça uso da calculadora, porque o objetivo da atividade é verificar se o aluno irá criar estratégias diversas para solucionar o problema. Com o uso da calculadora o aluno terá mais tempo para pensar nas possíveis soluções e criar estratégias. O uso da calculadora é recomendado para aprimorar o cálculo mental, estimativa e contribui para a compreensão do processo de resolução. Sugestão: Acrescente uma condicionante no problema, por exemplo: utilizar no mínimo duas operações”.
Propósito: Consolidar a aprendizagem de participação ativa na resolução de problemas com mais de uma solução.
Discuta com a turma:
- Qual a pergunta para o problema?
- Quais estratégias você pensou para explicar a solução do problema?
- Quais maneiras foram pensadas para descrever as soluções encontradas?
- O uso da calculadora ajudou a elaborar novas estratégias?
Materiais complementares para impressão:
Sugestão de adaptação para ensino remoto
Código do plano
MAT8_26RDP04
Recursos
- Necessários:
- caderno
- lápis
- calculadora
- grupo de alunos no WhatsApp
- Opcionais:
- Google Sala de Aula
- Meet
- Zoom
- Padlet
- Jamboard
Dicas de uso do Jamboard no link: https://support.google.com/jamboard/#topic=7383644
Para este plano, foque na etapa: Raio X.
Atividade Raio X
Para a realização dessa atividade, o aluno precisa ter em mãos a situação-problema. Você pode enviar uma foto do problema via WhatsApp e montar um Painel de Soluções, com um exemplo, como mostrado na Tabela da resolução dessa Atividade, disponível para acesso no link: https://nova-escola-producao.s3.amazonaws.com/q3rNRRTZwE86UWcuk5pugg2FXHAmWJTpmXv2sxfsdGJT8kX3Ar7E3BDw4JvG/resol-ativraiox-mat8-26rdp04.pdf,
utilizando o Padlet, o Jamboard, ou produzir um arquivo de forma que todos possam ter acesso. Essa Atividade favorece o trabalho individual, oriente os alunos para que leiam o problema e criem estratégias com o uso da calculadora, que mostrem uma ou mais soluções dessa situação problema, eles poderão fazer uma Tabela para organizar as possibilidades de resolução. Com o uso da calculadora o aluno terá mais tempo para pensar nas possíveis soluções e criar estratégias. O uso da calculadora é recomendado para aprimorar o cálculo mental, estimativa e contribui para a compreensão do processo de resolução. Sugestão: Acrescente uma condicionante no problema, por exemplo: "utilizar no mínimo duas operações". Se o aluno apresentar dificuldades para compreender e explanar suas estratégias, oralmente ou através do registro na Tabela, sugiro que proponha o jogo online “Calculadora Quebrada” disponível no link https://rachacuca.com.br/jogos/calculadora-quebrada//(acesso em 04 de jul 2020). Neste jogo os alunos devem usar operações matemáticas (soma, subtração, divisão e divisão) e os números disponíveis para obter os números procurados. Solicite que fotografem ou filmem suas estratégias e respostas, para compartilhar com a turma no momento da discussão das soluções.
Discussão das soluções
Professor, verifique as orientações feitas na resolução dessa Atividade, elas serão úteis na condução dessa discussão. A escuta das possíveis soluções é muito importante. Deixe que os alunos compartilhem suas respostas, seja por áudio, vídeo ou fotos se a aula for síncrona, ou por meio do Painel de Soluções interativo, no Padlet, no Jamboard, ou ainda em um arquivo de forma que todos possam ter acesso.
Convite às famílias
Sugira aos alunos que envolvam os familiares na discussão das estratégias para chegar às soluções, podem usar as calculadoras dos celulares, é um bom momento para interação lúdica e troca de conhecimentos. Entretanto, é importante tomar cuidado porque, apesar da indicação, as pessoas que convivem com os alunos nesse momento de reclusãol, podem estar envolvidos com outros afazeres.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Érica Fernanda Barbosa dos Santos.
Mentor: Tatiane Cristina Guadagnucci.
Especialista de área: Rita Batista.
Habilidade da BNCC
NÃO HÁ.
Objetivos específicos
Resolver e elaborar problemas que envolvam cálculos mentais ou escritos com números naturais, por meio de estratégias variadas, com compreensão dos processos neles envolvidos com e sem uso de calculadora.
Conceito-chave
Investigar diferentes soluções para situações problemas.
Recursos necessários
- Folha de papel A4 branca;
- Atividades impressas em folhas, coladas no caderno ou não.