Aquecimento
Plano de Aula
Plano de aula: Reconhecendo padrões para divisões
Plano 4 de uma sequência de 5 planos. Veja todos os planos sobre Múltiplos, divisores e critérios de divisibilidade dos números naturais
Por: Emanuelle Martins
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Emanuelle Martins
Mentor: Rodrigo Morozetti Blanco
Especialista: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
- (EF06MA04) Classificar números naturais em primos e compostos, estabelecer relações entre números, expressas pelos termos “é múltiplo de”, “é divisor de”, “é fator de”, e estabelecer, por meio de investigações, critérios de divisibilidade por 2, 3, 4, 5, 6, 8, 9, 10, 100 e 1000.
- (EF06MA05) Resolver e elaborar problemas que envolvam as ideias de múltiplo e de divisor.
Objetivos específicos
- Reconhecer padrões para divisões.
Conceitos-chave
Para um número ser divisível por dois ele deve ser par, ou seja, a casa das unidades precisa ser: 0, 2, 4, 6 ou 8. Podemos dizer que a casa das unidades varia de duas em duas unidades.
Para um número ser divisível por 3, devemos somar seus algarismo e obter um número que seja múltiplo de três
Para um número ser divisível por 6 ele precisa ser divisível por 2 e por 3 ao mesmo tempo.
Para um número ser divisível por cinco ele precisa ter em sua casa das unidades o zero ou o cinco, ou seja, a casa das unidades de variar de cinco em cinco unidades.
Recursos necessários
- Atividades impressas em folhas, coladas no caderno ou não;
- Projetor Multimídia.
Habilidades BNCC:
Objetivos de aprendizagem
- Reconhecer padrões para divisões.
Resumo da aula
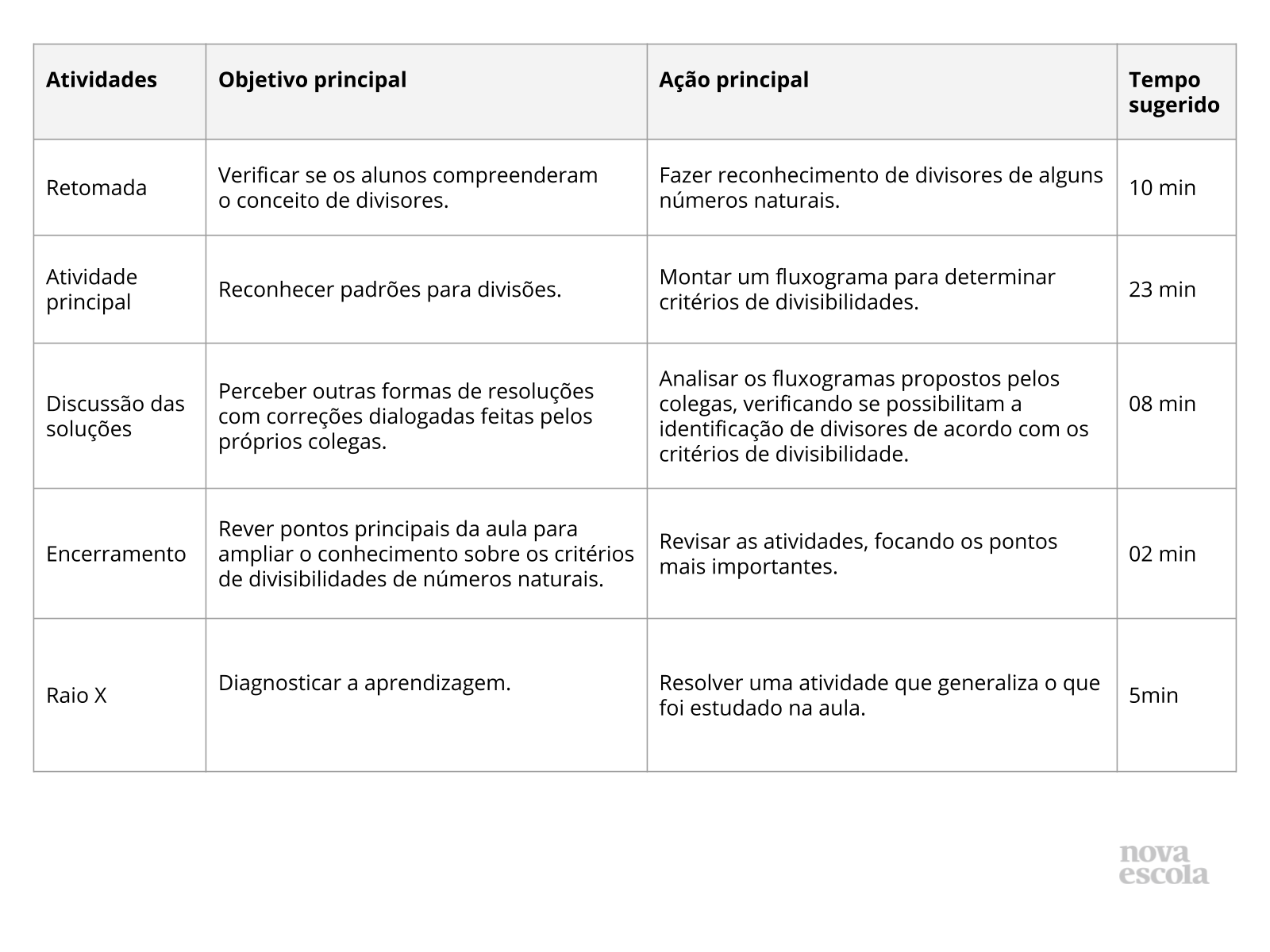
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 02 minutos
Orientação: Professor, leia para seus alunos o objetivo da aula.
Propósito: orientar os alunos sobre o que se pretende aprender nesta aula.
Retomada
Tempo sugerido: 10 minutos (Slides 3 e 4)
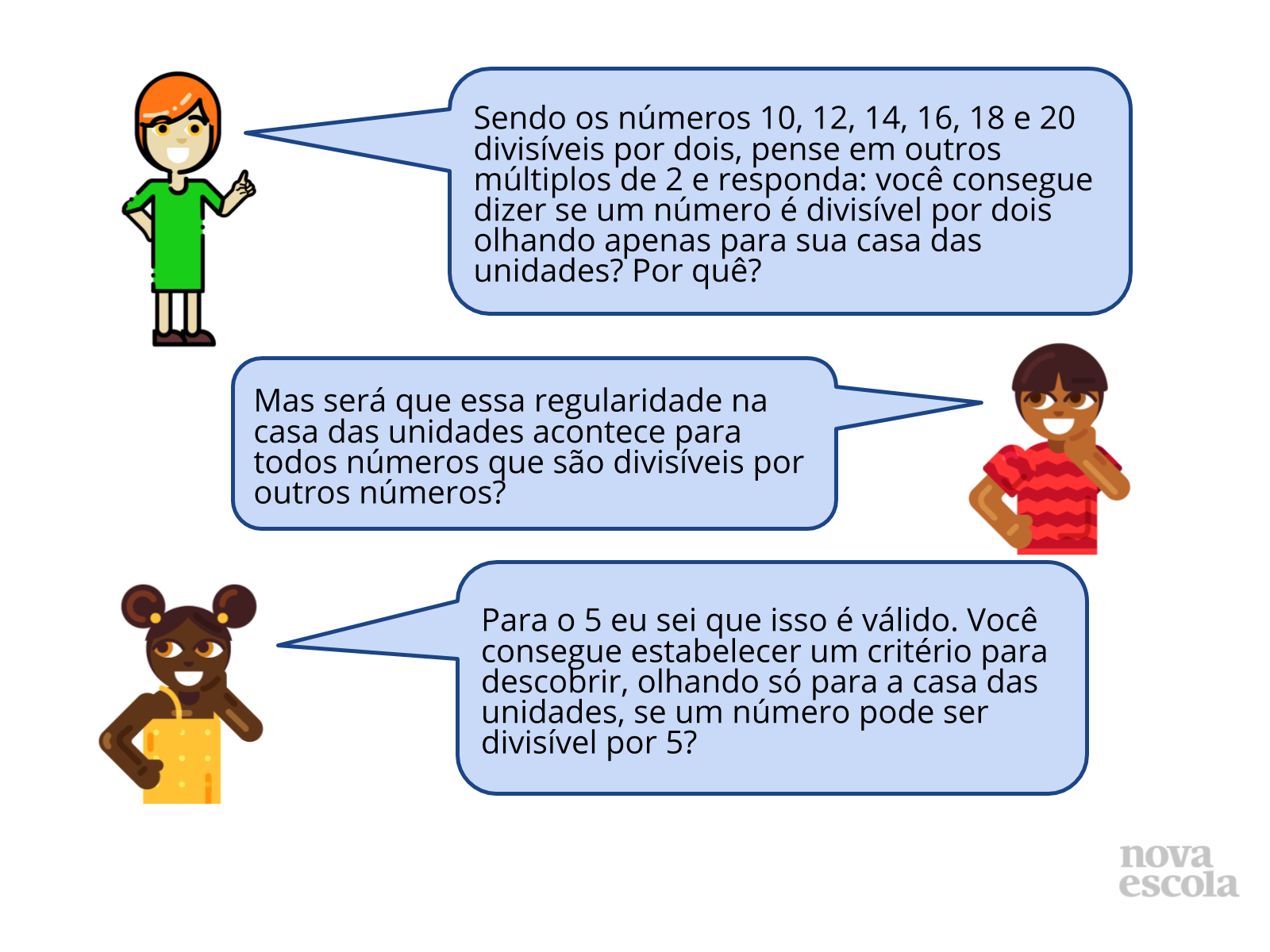
Orientação: Professor, esta atividade está apresentada nos slides 3 e 4, onde através das ideias e dos questionamentos apresentados pelos personagens nos slides, espera-se que os alunos consigam retomar a ideia de um número ser divisível por outro número, e consigam estabelecer critérios de divisibilidade. Divida o quadro em 5 espaços, e em cada um desses espaços escreva os apontamentos feitos por seus alunos sobre os critérios de divisibilidade por 2, por 3, por 6, por 5 e por 10. A intenção é eles perceberem que ao estabelecer critérios, fica mais prático descobrir quando que um número é divisível por outro número.
Discuta com a turma:
- Será que é necessário efetuarmos sempre o cálculo de divisão para saber se um número é divisível por outro número?
- Qual a principal finalidade em estabelecermos critérios de divisibilidade?
- Você consegue pensar em critérios de divisibilidade para outros números que não foram questionados nos slides? Quais? Como pensou?
Materiais complementares para impressão:
Retomada
Tempo sugerido: 10 minutos (Slides 3 e 4)
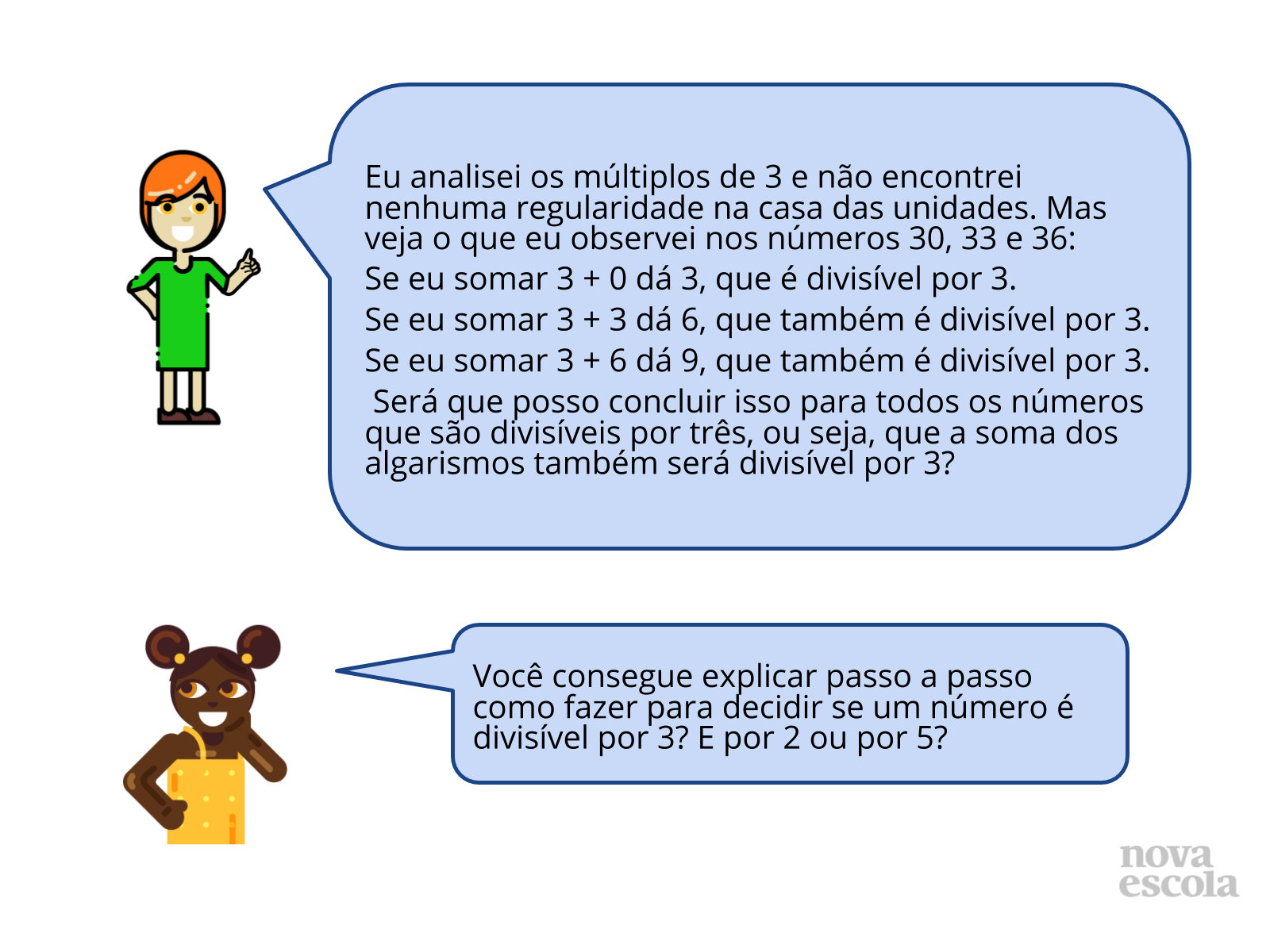
Orientação: Professor, esta atividade está apresentada nos slides 3 e 4, onde através das ideias e dos questionamentos apresentados pelos personagens nos slides, espera-se que os alunos consigam retomar a ideia de um número ser divisível por outro número, e consigam estabelecer critérios de divisibilidade. Divida o quadro em 5 espaços, e em cada um desses espaços escreva os apontamentos feitos por seus alunos sobre os critérios de divisibilidade por 2, por 3, por 6, por 5 e por 10. A intenção é eles perceberem que ao estabelecer critérios, fica mais prático descobrir quando que um número é divisível por outro número.
Discuta com a turma:
- Será que é necessário efetuarmos sempre o cálculo de divisão para saber se um número é divisível por outro número?
- Qual a principal finalidade em estabelecermos critérios de divisibilidade?
- Você consegue pensar em critérios de divisibilidade para outros números que não foram questionados nos slides? Quais? Como pensou?
Atividade principal

Tempo sugerido: 23 minutos (Slides 5 a 7)
Orientação: Professor, veja se os alunos entendem os passos listados para decidir se um número é ou não divisível por 3. Veja também se a lista colocada aqui é condizente com as respostas que eles deram para a atividade anterior. Em seguida, mostre o fluxograma no slide 6 e faça com eles os testes citados, da seguinte maneira:
- Para o número 4275 a soma dos algarismos é 4 + 2 + 7 + 5 = 18. Como 18 é maior que 9, devemos somar de novo. O resultado é 1 + 8 = 9. Como o resultado está entre 0 e 9, passamos para o próximo losango. Como o resultado é 9 a resposta é sim, o número é divisível por 3.
- Para o número 701 a soma dos algarismos é 7 + 0 + 1 = 8. Como o resultado está entre 0 e 9, passamos para o próximo losango. Como o resultado é 8 (não é 3, nem 6, nem 9), o número não é divisível por 3.
Se achar pertinente, divida 4275 e 701 por 3 para que eles vejam que a primeira divisão é exata e a segunda não é. Organize então a sala em duplas ou em pequenos grupos para realizar a atividade proposta no slide 7. Entregue a cada dupla uma cartolina e uma folha com as figuras geométricas impressas. Se possível, enquanto eles fazem a atividade, deixe na lousa o exemplo do slide 6 .
Durante a execução da atividade, relembre-os de usar corretamente os balões de acordo com os formatos. Para fazer as setas eles podem usar caneta hidrográfica preta, mas oriente-os a fazer primeiro a lápis, e deixem para colar as formas na cartolina e passar as setas à caneta apenas quando o fluxograma estiver pronto. Fique atento para que não coloquem nos losangos nenhuma pergunta cuja resposta não seja de “sim ou não”, ou cuja resposta seja por si só o que se deseja saber. Para isso, combine com eles alguns detalhes como, por exemplo, considerar que o fluxograma será testado por um computador que não sabe dividir e não sabe a tabuada de cor. Isso evitará que eles coloquem no losango algo como “veja se o número é múltiplo de 3”.
Peça sempre para que testem os fluxogramas passo a passo, verificando se os resultados de saída estão corretos.
Propósito: aplicar um fluxograma para determinar divisibilidades.
Discuta com a turma:
- Alguém pode nos explicar porque temos desenhos geométricos diferentes para construir um fluxograma?
- Você sabe explicar qual é a finalidade de um fluxograma?
- Por que o estudo dos critérios de divisibilidade se encaixa na construção de um fluxograma?
- Todo número múltiplo de 2 é múltiplo de 6?
- Todo número múltiplo de 6 é múltiplo de 2?
- Você sabe dizer se um número é ou não múltiplo de 10 sem testar a divisibilidade do 2 e do 5?
Materiais Complementares:
Você pode saber mais sobre fluxograma nesse link.
Atividade principal - Fluxograma
Atividade principal
Tempo sugerido: 23 minutos (Slides 5 a 7)
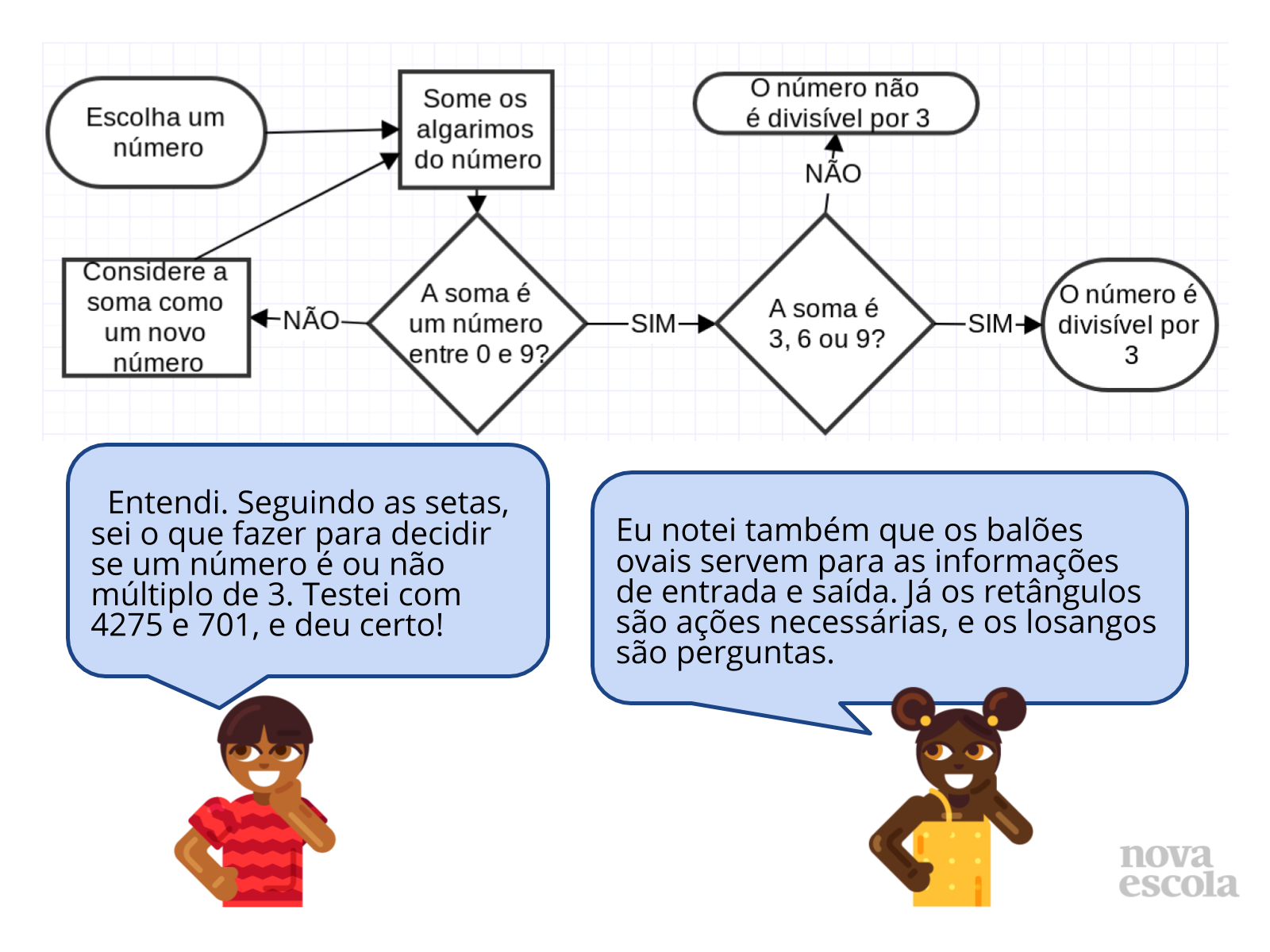
Orientação: Professor, veja se os alunos entendem os passos listados para decidir se um número é ou não divisível por 3. Veja também se a lista colocada aqui é condizente com as respostas que eles deram para a atividade anterior. Em seguida, mostre o fluxograma no slide 6 e faça com eles os testes citados, da seguinte maneira:
- Para o número 4275 a soma dos algarismos é 4 + 2 + 7 + 5 = 18. Como 18 é maior que 9, devemos somar de novo. O resultado é 1 + 8 = 9. Como o resultado está entre 0 e 9, passamos para o próximo losango. Como o resultado é 9 a resposta é sim, o número é divisível por 3.
- Para o número 701 a soma dos algarismos é 7 + 0 + 1 = 8. Como o resultado está entre 0 e 9, passamos para o próximo losango. Como o resultado é 8 (não é 3, nem 6, nem 9), o número não é divisível por 3.
Se achar pertinente, divida 4275 e 701 por 3 para que eles vejam que a primeira divisão é exata e a segunda não é. Organize então a sala em duplas ou em pequenos grupos para realizar a atividade proposta no slide 7. Entregue a cada dupla uma cartolina e uma folha com as figuras geométricas impressas. Se possível, enquanto eles fazem a atividade, deixe na lousa o exemplo do slide 6 .
Durante a execução da atividade, relembre-os de usar corretamente os balões de acordo com os formatos. Para fazer as setas eles podem usar caneta hidrográfica preta, mas oriente-os a fazer primeiro a lápis, e deixem para colar as formas na cartolina e passar as setas à caneta apenas quando o fluxograma estiver pronto. Peça sempre para que testem os fluxogramas passo a passo, verificando se os resultados de saída estão corretos.
Propósito: aplicar um fluxograma para determinar divisibilidades.
Discuta com a turma:
- Alguém pode nos explicar porque temos desenhos geométricos diferentes para construir um fluxograma?
- Você sabe explicar qual é a finalidade de um fluxograma?
- Por que o estudo dos critérios de divisibilidade se encaixa na construção de um fluxograma?
- Todo número múltiplo de 2 é múltiplo de 6?
- Todo número múltiplo de 6 é múltiplo de 2?
- Você sabe dizer se um número é ou não múltiplo de 10 sem testar a divisibilidade do 2 e do 5?
Atividade principal

Tempo sugerido: 23 minutos (Slides 5 a 7)
Orientação: Professor, veja se os alunos entendem os passos listados para decidir se um número é ou não divisível por 3. Veja também se a lista colocada aqui é condizente com as respostas que eles deram para a atividade anterior. Em seguida, mostre o fluxograma no slide 6 e faça com eles os testes citados, da seguinte maneira:
- Para o número 4275 a soma dos algarismos é 4 + 2 + 7 + 5 = 18. Como 18 é maior que 9, devemos somar de novo. O resultado é 1 + 8 = 9. Como o resultado está entre 0 e 9, passamos para o próximo losango. Como o resultado é 9 a resposta é sim, o número é divisível por 3.
- Para o número 701 a soma dos algarismos é 7 + 0 + 1 = 8. Como o resultado está entre 0 e 9, passamos para o próximo losango. Como o resultado é 8 (não é 3, nem 6, nem 9), o número não é divisível por 3.
Se achar pertinente, divida 4275 e 701 por 3 para que eles vejam que a primeira divisão é exata e a segunda não é. Organize então a sala em duplas ou em pequenos grupos para realizar a atividade proposta no slide 7. Entregue a cada dupla uma cartolina e uma folha com as figuras geométricas impressas. Se possível, enquanto eles fazem a atividade, deixe na lousa o exemplo do slide 6 .
Durante a execução da atividade, relembre-os de usar corretamente os balões de acordo com os formatos. Para fazer as setas eles podem usar caneta hidrográfica preta, mas oriente-os a fazer primeiro a lápis, e deixem para colar as formas na cartolina e passar as setas à caneta apenas quando o fluxograma estiver pronto. Peça sempre para que testem os fluxogramas passo a passo, verificando se os resultados de saída estão corretos.
Propósito: aplicar um fluxograma para determinar divisibilidades.
Discuta com a turma:
- Alguém pode nos explicar porque temos desenhos geométricos diferentes para construir um fluxograma?
- Você sabe explicar qual é a finalidade de um fluxograma?
- Por que o estudo dos critérios de divisibilidade se encaixa na construção de um fluxograma?
- Todo número múltiplo de 2 é múltiplo de 6?
- Todo número múltiplo de 6 é múltiplo de 2?
- Você sabe dizer se um número é ou não múltiplo de 10 sem testar a divisibilidade do 2 e do 5?
Discussão de soluções
Tempo sugerido: 8 minutos (slides 8 e 9)
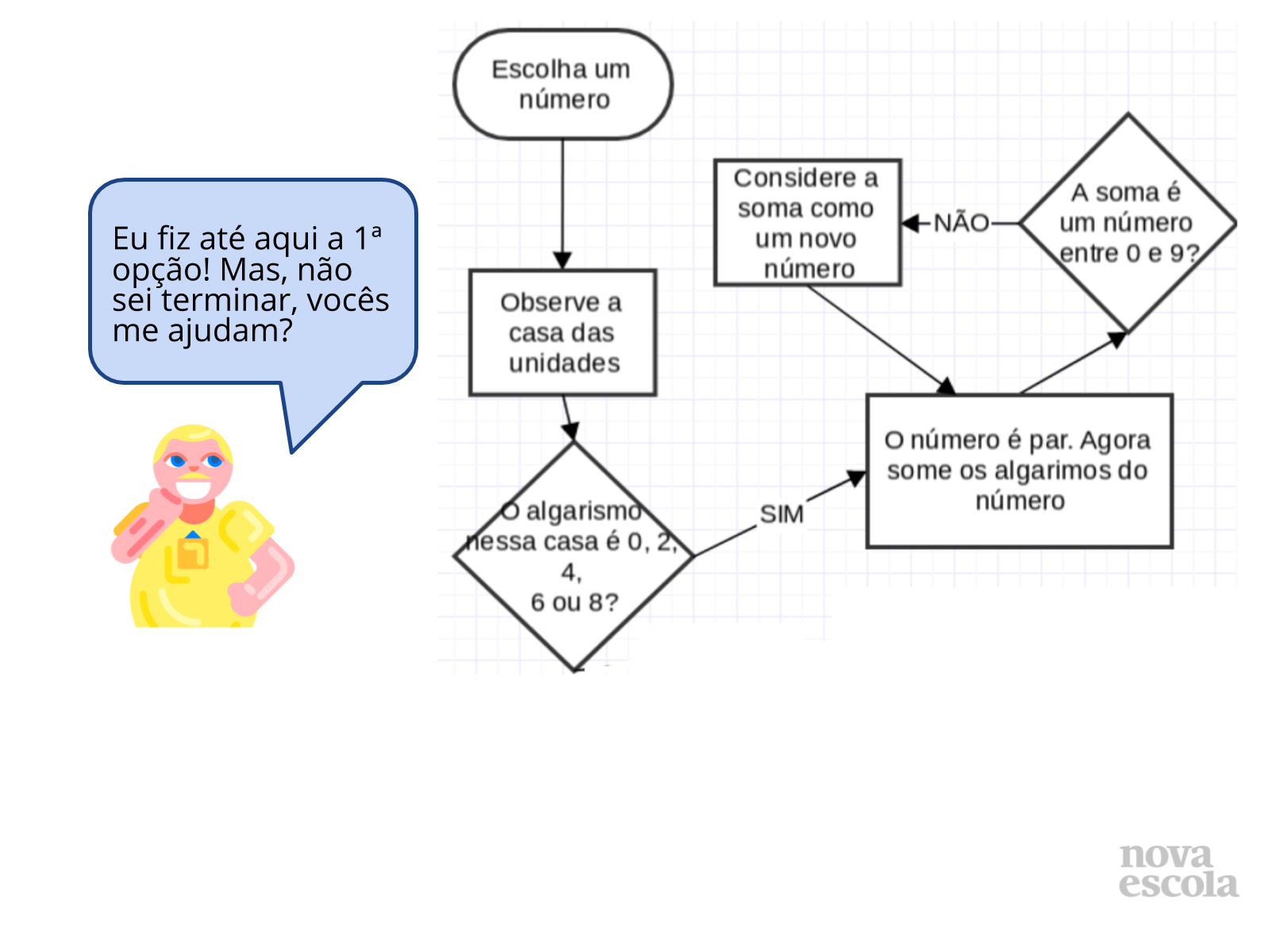
Orientação: Professor, a partir das possíveis partes de soluções apresentadas, estimule seus alunos a completarem as partes faltantes, dando sentido correto aos fluxogramas apresentados. Para isso eles podem buscar semelhanças e diferenças em suas próprias soluções, e assim irem aprendendo formas diferenciadas.
Propósito: Apresentar parte de possíveis soluções para que os alunos analisem se elas estão corretas, e completem as partes faltantes.
Discuta com a turma:
- As partes dos fluxogramas apresentadas estão corretas? Por que?
- Os critérios de divisibilidade exigidos estão corretos? Por que?
- Alguém pode nos dar uma ideia de como completar as partes faltantes?
- Será que existem outras formas de fazer as partes faltantes? Alguém tem outra ideia?
Discussão de soluções
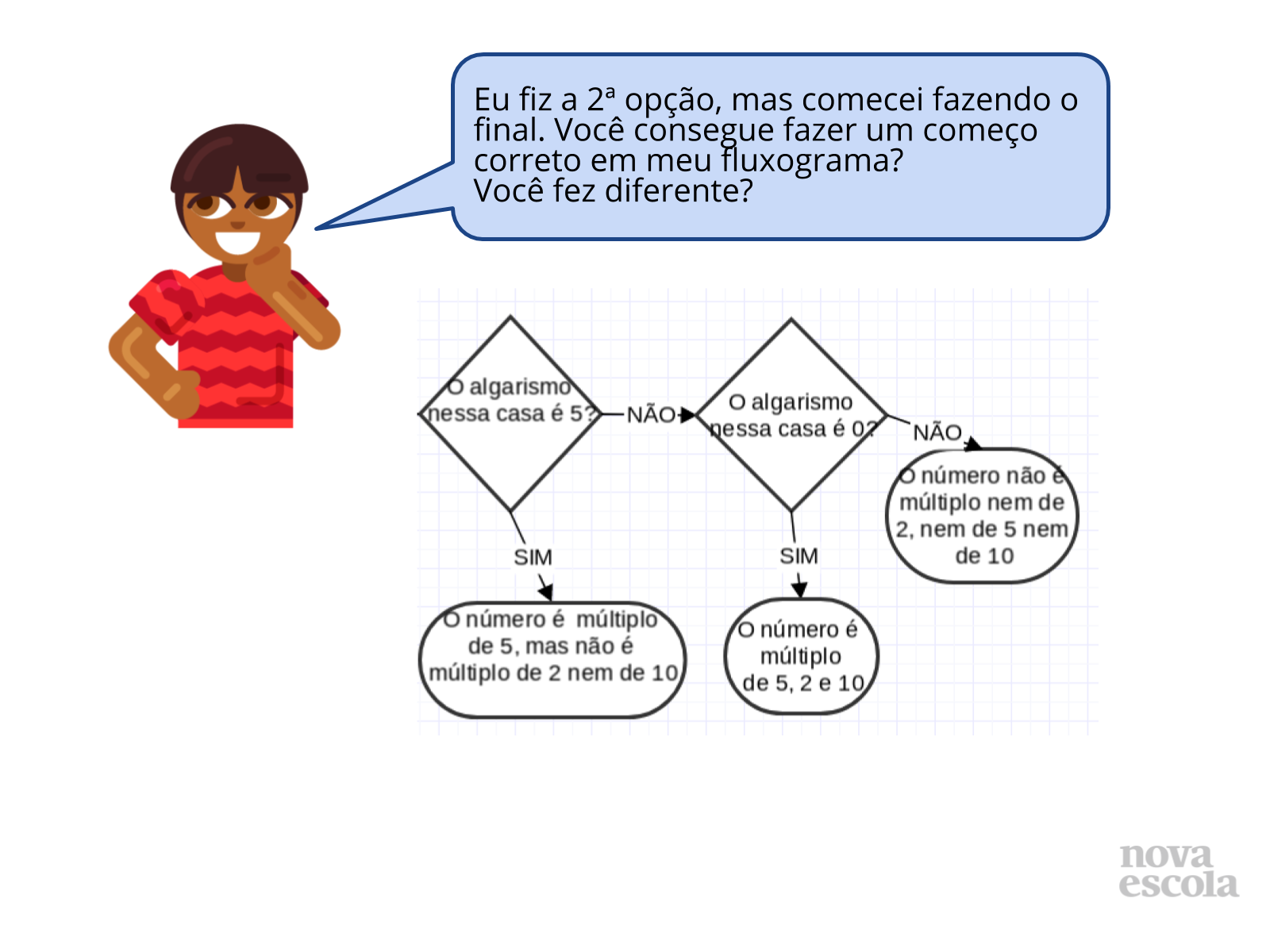
Tempo sugerido: 8 minutos (slides 8 e 9)
Orientação: Professor, a partir das possíveis partes de soluções apresentadas, estimule seus alunos a completarem as partes faltantes, dando sentido correto aos fluxogramas apresentados. Para isso eles podem buscar semelhanças e diferenças em suas próprias soluções, e assim irem aprendendo formas diferenciadas.
Propósito: Apresentar parte de possíveis soluções para que os alunos analisem se elas estão corretas, e completem as partes faltantes.
Discuta com a turma:
- As partes dos fluxogramas apresentadas estão corretas? Por que?
- Os critérios de divisibilidade exigidos estão corretos? Por que?
- Alguém pode nos dar uma ideia de como completar as partes faltantes?
- Será que existem outras formas de fazer as partes faltantes? Alguém tem outra ideia?
Encerramento

Tempo sugerido: 2 minutos
Orientação: Professor, peça para algum aluno ler o que foi estudado nesta aula.
Propósito: Expor e ler o que foi estudado na aula para fixar a aprendizagem.
Discuta com a turma:
- Alguém pode nos dar exemplos de números divisíveis por 2? Por 3? Por 6? E Por 5?
- Alguém pode nos dizer alguns números que são divisíveis por 2 e por 3 ao mesmo tempo? Por que ele também é divisível por 6?
Raio X

Tempo sugerido: 05 minutos
Orientação: Entregue esta atividade para cada aluno resolver sozinho, pois através dela você irá verificar a aprendizagem de seus alunos sobre o tema da aula.
Propósito: Diagnosticar a aprendizagem através de uma atividade que envolve o conteúdo estudado nesta aula.
Materiais complementares para impressão:
Código do plano: MAT6_02NUM04
Recursos
- Necessários: Caderno, lápis, borracha, grupo de WhatsApp, vídeo Khan Academy https://pt.khanacademy.org/math/pre-algebra/pre-algebra-factors-multiples/pre-algebra-divisibility-tests/v/recognizing-divisibility
- Opcionais: Minuto Mathema – Existe regra de divisibilidade por 7?
https://www.youtube.com/watch?v=GS2wdyQoN-4
Para este plano, foque na etapa: Retomada
Retomada
Professor, a atividade é uma retomada de conceitos que são fundamentais para o desenvolvimento da aula. Numa proposta síncrona e colaborativa, você pode propor os questionamentos apresentados no primeiro slide de Retomada usando um editor de texto (Google Docs, por exemplo), de modo que os alunos possam respondê-los. Você também pode usar a função de áudio do WhatsApp para que cada aluno possa postar suas respostas ou hipóteses sobre a questão disparadora. Explique que é um momento de retomada de conteúdos e que caso tenham dúvidas, estas serão trabalhadas no decorrer da aula.
Discussão das soluções
Fique atento às respostas dos alunos. Se na primeira pergunta eles responderem que sim, pelo fato de serem números pares, conclua, junto com eles, que todo número par é divisível por 2.
Na terceira pergunta, instigue os alunos a observar se a mesma regularidade usada nos números divisíveis por 2 pode ser observada nos números divisíveis por 5. Sugira a eles que confiram se os números 10, 12, 13, 15, 17, 20 e 35 são divisíveis por 5. Finalize essa conversa garantindo que eles consigam estabelecer o critério de divisibilidade por 5. Continue a conversa com os alunos, compartilhando o segundo slide de Retomada, para que os alunos possam estabelecer também o critério de divisibilidade por 3, assim como foi feito nos dois critérios anteriores.
Solicite como tarefa que os alunos gravem áudios ou podcasts explicando o passo a passo dos critérios de divisibilidade por 2, 3 e 5. Para finalizar, proponha aos alunos que assistam ao vídeo do Khan Academy - Reconhecimento de divisibilidade
https://pt.khanacademy.org/math/pre-algebra/pre-algebra-factors-multiples/pre-algebra-divisibility-tests/v/recognizing-divisibility
Convite às famílias
A participação das famílias no processo de aprendizagem é de grande importância para o aluno. Porém, ressaltamos que os pais não são professores de matemática e muitos estão ocupados nessa fase com outras funções em casa.
Questione os alunos sobre o critério de divisibilidade por 7. Será que existe? Para que servem esses critérios? Por que não existe critério de divisibilidade para todos os números? Quer saber as respostas dessas perguntas? Assista ao vídeo Minuto Mathema – Existe regra de divisibilidade por 7, e convide sua família para compartilhar essa aprendizagem. https://www.youtube.com/watch?v=GS2wdyQoN-4
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Emanuelle Martins
Mentor: Rodrigo Morozetti Blanco
Especialista: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
- (EF06MA04) Classificar números naturais em primos e compostos, estabelecer relações entre números, expressas pelos termos “é múltiplo de”, “é divisor de”, “é fator de”, e estabelecer, por meio de investigações, critérios de divisibilidade por 2, 3, 4, 5, 6, 8, 9, 10, 100 e 1000.
- (EF06MA05) Resolver e elaborar problemas que envolvam as ideias de múltiplo e de divisor.
Objetivos específicos
- Reconhecer padrões para divisões.
Conceitos-chave
Para um número ser divisível por dois ele deve ser par, ou seja, a casa das unidades precisa ser: 0, 2, 4, 6 ou 8. Podemos dizer que a casa das unidades varia de duas em duas unidades.
Para um número ser divisível por 3, devemos somar seus algarismo e obter um número que seja múltiplo de três
Para um número ser divisível por 6 ele precisa ser divisível por 2 e por 3 ao mesmo tempo.
Para um número ser divisível por cinco ele precisa ter em sua casa das unidades o zero ou o cinco, ou seja, a casa das unidades de variar de cinco em cinco unidades.
Recursos necessários
- Atividades impressas em folhas, coladas no caderno ou não;
- Projetor Multimídia.










