Resumo da aula
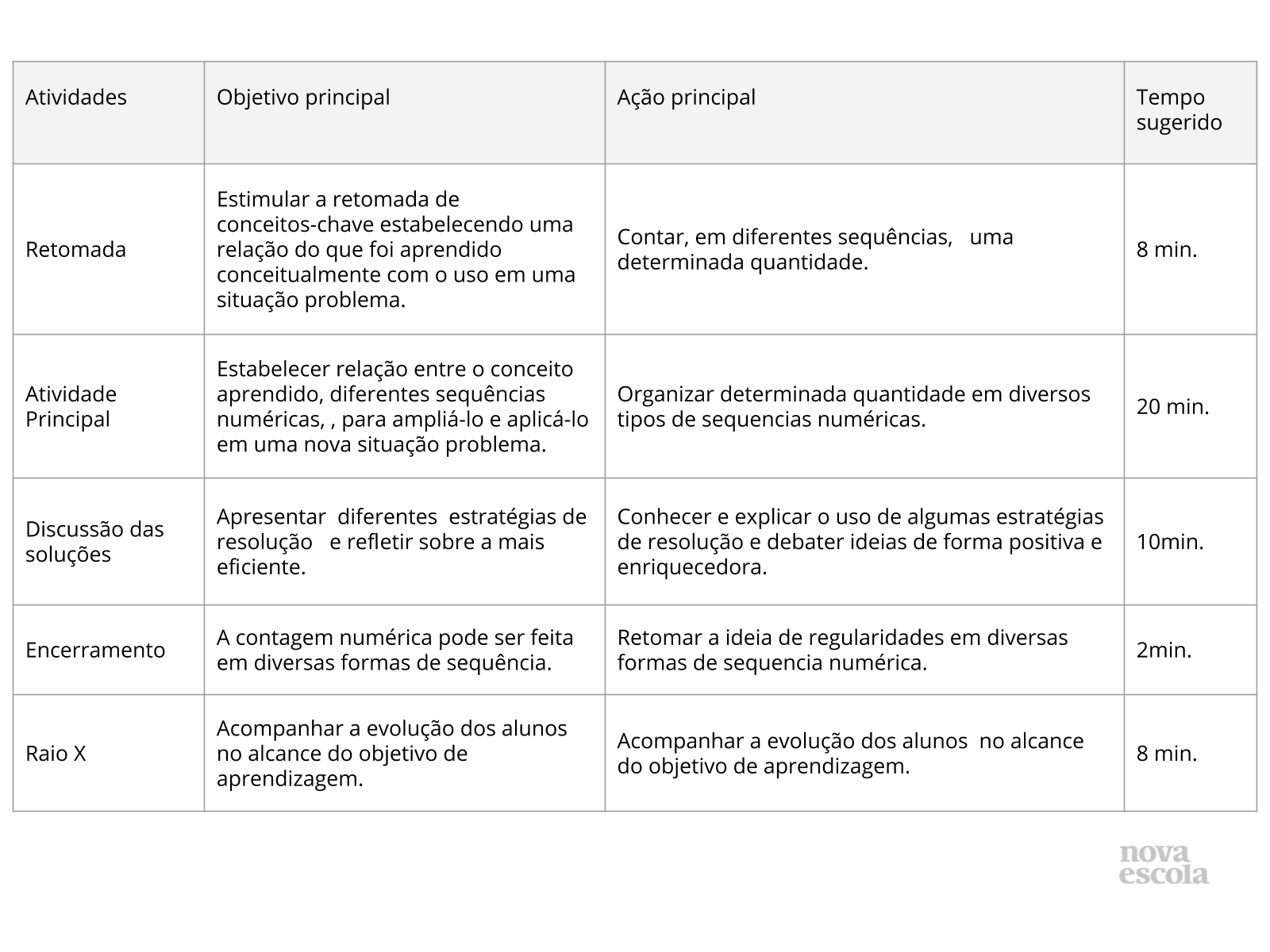
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos
Orientação: Projete ou leia o objetivo para a turma, usando uma linguagem mais simples para as crianças.
Propósito: Compartilhar o objetivo da aula.
Retomada

Tempo sugerido: 8 minutos (Slides 3 e 4).
Orientações: Organize para essa aula os materiais listados no arquivo “Sobre o plano”. Separe os alunos formando grupos com 4 alunos. Cada grupo deverá ter seu próprio fio de contas. Utilize o fio de contas do professor para prendendo-o no quadro para que a turma tenha uma melhor visualização. Primeiramente, deixe que explorem o fio, contando quantas bolinhas existem, observando a organização das sequências de cores, etc.
Observação: o FIO DE CONTAS é um material de apoio à Matemática. Através dele os alunos podem fazer contagens simples, de 2 em 2, de 3 em 3 (…), somar, subtrair e resolver situações problemas. Este material didático é extremamente útil para trabalhar a ideia de quantidade, para a construção de conceito de número e para contagem e pequenos cálculos, tornando as quantidades e suas representações simbólicas bastante familiares às crianças.
Propósito: Contar, em diferentes sequências, uma determinada quantidade.
Discuta com a turma:
Estou com algumas dúvidas, ajudem-me a resolvê-las:
- Se eu contar de 2 em 2 consigo parar no número 5?
- Contando de 2 em 2 consigo chegar no número 14? Quantos “dois” foi preciso contar?
- Se eu contar de 5 em 5 consigo parar no número 12?
- Estando no número 7, quantos “cincos” terei que contar?
Material Complementar:
Aquecimento
Resolução do Aquecimento
Retomada

Tempo sugerido: 8 minutos (Slides 3 e 4).
Orientação: Siga, após o manuseio do material, propondo alguns questionamentos para que o grupo reflita, discuta e execute a tarefa a fim de solucioná-la. Entregue para cada grupo de crianças a atividade impressa e deixe que conversem entre si para resolvê-la. Após perceber que todos já concluíram, promova a exposição dos resultados em uma conversa coletiva.
Propósito: Contar, em diferentes sequências, uma determinada quantidade.
Material complementar:
Aquecimento
Resolução do Aquecimento
Atividade principal

Tempo sugerido: 20 minutos
Orientação: Utilize o seu colar de contas feito de bolinhas maiores e reorganize as contas de forma a ficar no formato desse colar. Apresente a situação para a sua turma, projete o slide ou escreva no quadro, fazendo a leitura para que todos a compreendam. Primeiramente, deixe que observem bem o fio de contas preso no quadro com a nova disposição das bolinhas. As crianças poderão também reorganizar o seu próprio fio de contas usando pregadores de roupa ou clipes para fazer a separação de acordo com a imagem. Caso não tenha o material disponível para essa reorganização, entregue uma cópia do modelo do colar impressa para cada grupo. Nesta folha, os alunos poderão fazer as marcações que acharem necessárias para resolver como descobrir se João está certo ou não. Deixe um tempo para que cada grupo reflita, discuta e execute a tarefa a fim de solucioná-la.
Propósito: Organizar determinada quantidade em diversos tipos de sequências numéricas.
Discuta com a turma:
- Sem contar de um em um é possível perceber quantas contas possuem o colar?
- Como podemos contar essas contas de maneira mais rápida?
Materiais complementares:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Discussão das soluções
Tempo sugerido: 10 minutos (Slides 6 até 9)
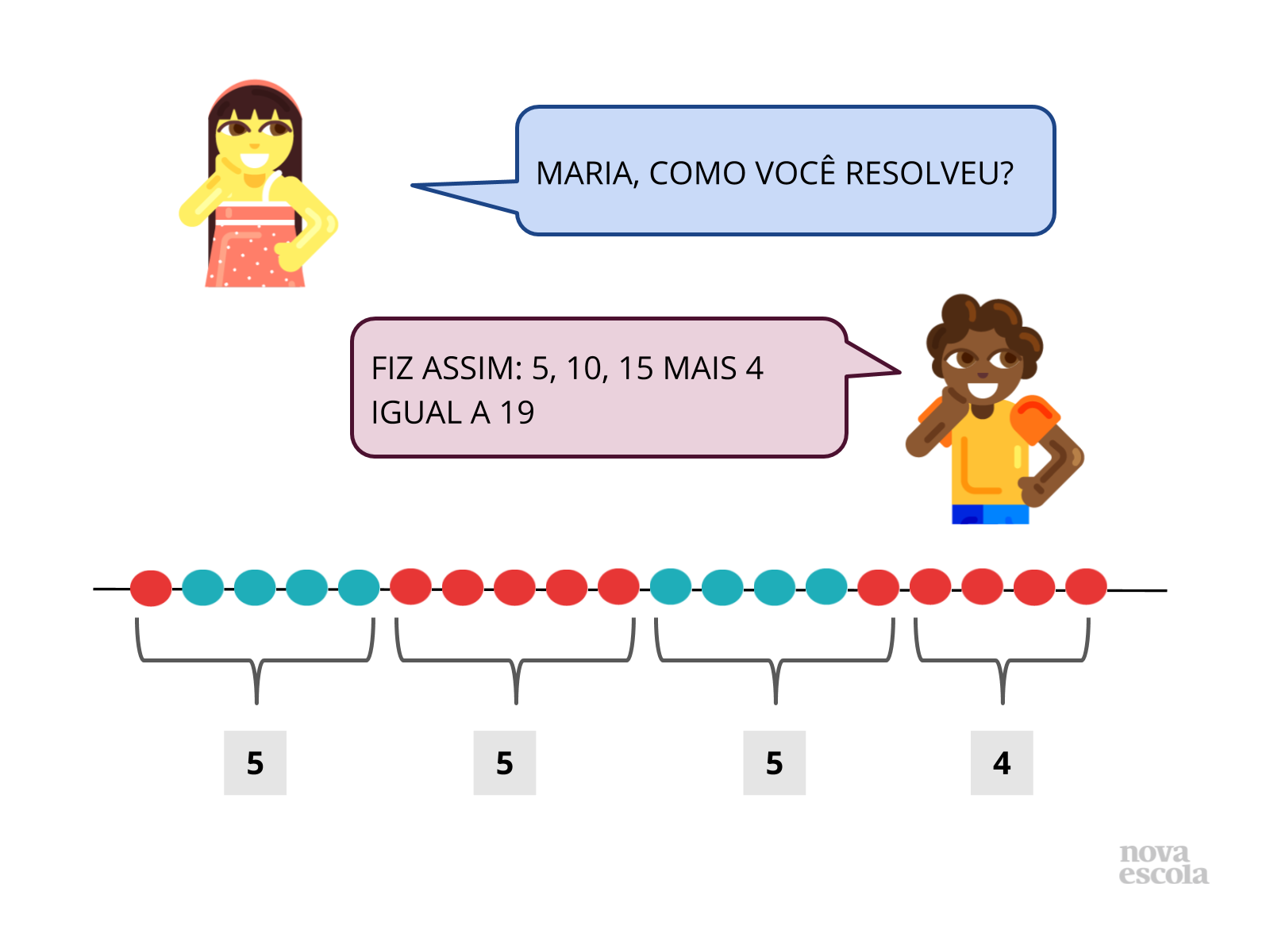
Orientação: Projete ou leia os slides para a turma. No painel de soluções apresentamos algumas possíveis formas para resolver a situação proposta que devem ser discutidas com as crianças. No entanto, é melhor explorar as resoluções que surgirem no contexto da sua aula. Nos exemplos dos slides, foram apresentadas três possíveis maneiras de estratégias que podem ser utilizadas pelas crianças (pode ser que existam outras). Proponha uma reflexão com os alunos levando-os a perceberem que mesmo utilizando maneiras diferentes de realizar as “somas”, os agrupamentos, as sequências, foi possível encontrar o mesmo resultado.
Propósito: Conhecer e explicar o uso de algumas estratégias de resolução utilizadas pelos alunos promovendo o debate de ideias de forma positiva e enriquecedora. Contribuir também para a análise de erros/dificuldades e valorizar as diferentes resoluções.
Discussão das soluções
Tempo sugerido: 10 minutos (Slides 6 até 9)
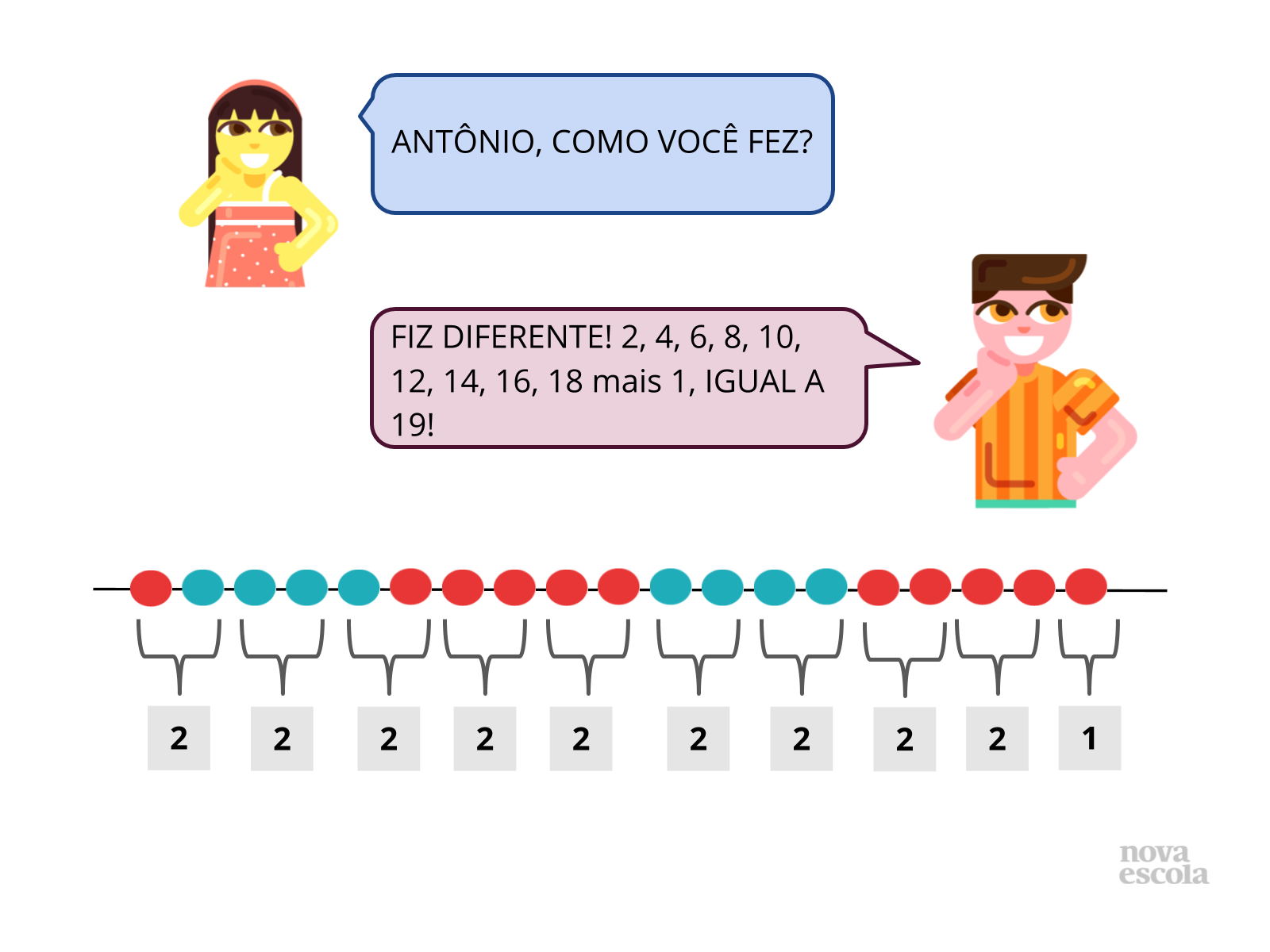
Orientação: Projete ou leia os slides para a turma. No painel de soluções apresentamos algumas possíveis formas para resolver a situação proposta que devem ser discutidas com as crianças. No entanto, é melhor explorar as resoluções que surgirem no contexto da sua aula. Nos exemplos dos slides, foram apresentadas três possíveis maneiras de estratégias que podem ser utilizadas pelas crianças (pode ser que existam outras). Proponha uma reflexão com os alunos levando-os a perceberem que mesmo utilizando maneiras diferentes de realizar as “somas”, os agrupamentos, as sequências, foi possível encontrar o mesmo resultado.
Propósito: Conhecer e explicar o uso de algumas estratégias de resolução utilizadas pelos alunos promovendo o debate de ideias de forma positiva e enriquecedora. Contribuir também para a análise de erros/dificuldades e valorizar as diferentes resoluções.
Discussão das soluções
Tempo sugerido: 10 minutos (Slides 6 até 9)
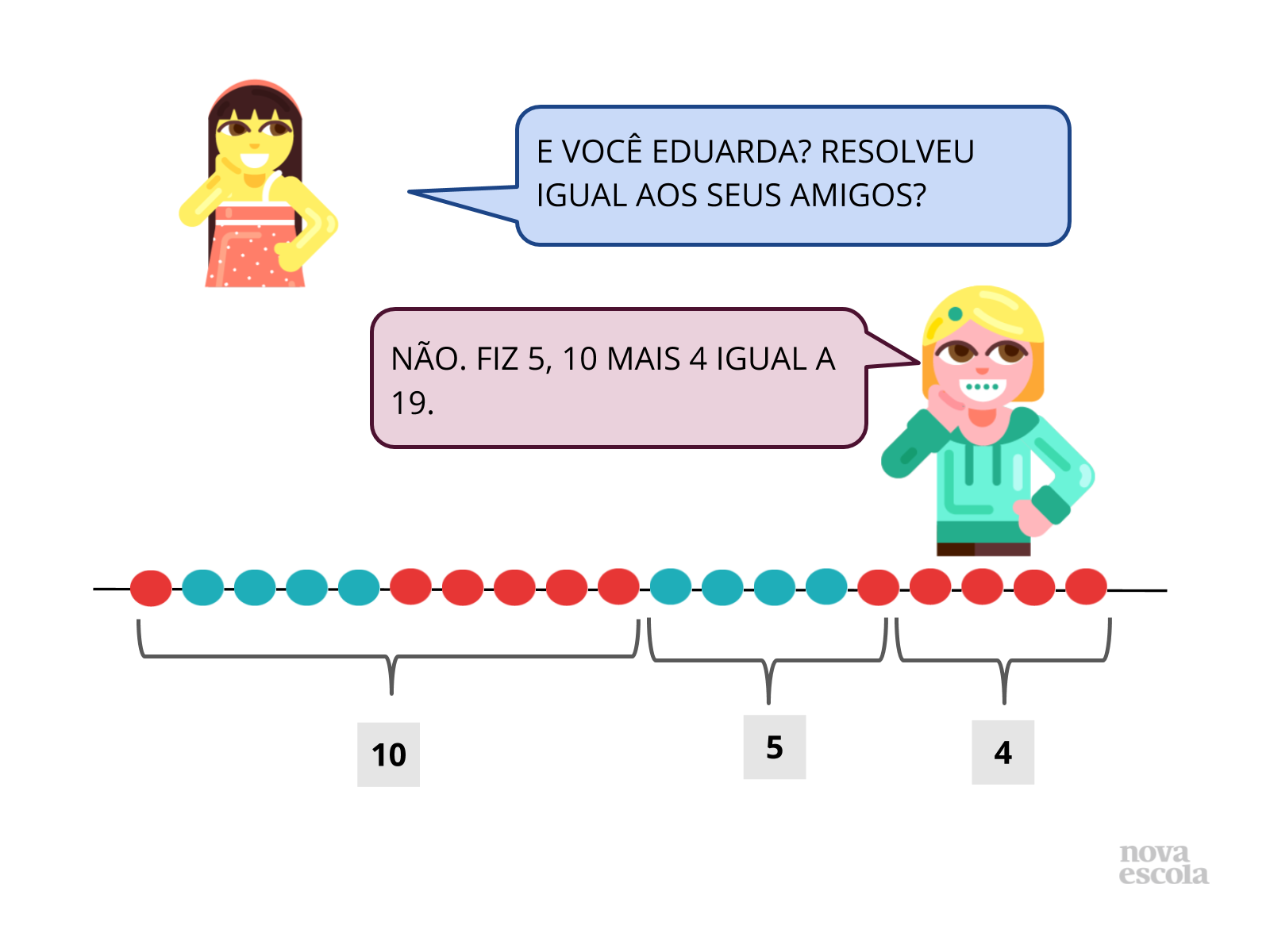
Orientação: Projete ou leia os slides para a turma. No painel de soluções apresentamos algumas possíveis formas para resolver a situação proposta que devem ser discutidas com as crianças. No entanto, é melhor explorar as resoluções que surgirem no contexto da sua aula. Nos exemplos dos slides, foram apresentadas três possíveis maneiras de estratégias que podem ser utilizadas pelas crianças (pode ser que existam outras). Proponha uma reflexão com os alunos levando-os a perceberem que mesmo utilizando maneiras diferentes de realizar as “somas”, os agrupamentos, as sequências, foi possível encontrar o mesmo resultado.
Propósito: Conhecer e explicar o uso de algumas estratégias de resolução utilizadas pelos alunos promovendo o debate de ideias de forma positiva e enriquecedora. Contribuir também para a análise de erros/dificuldades e valorizar as diferentes resoluções.
Discussão das soluções

Tempo sugerido: 10 minutos (Slides 6 até 9)
Orientação: Projete ou leia os slides para a turma. No painel de soluções apresentamos algumas possíveis formas para resolver a situação proposta que devem ser discutidas com as crianças. No entanto, é melhor explorar as resoluções que surgirem no contexto da sua aula. Nos exemplos dos slides, foram apresentadas três possíveis maneiras de estratégias que podem ser utilizadas pelas crianças (pode ser que existam outras). Proponha uma reflexão com os alunos levando-os a perceberem que mesmo utilizando maneiras diferentes de realizar as “somas”, os agrupamentos, as sequências, foi possível encontrar o mesmo resultado.
Propósito: Conhecer e explicar o uso de algumas estratégias de resolução utilizadas pelos alunos promovendo o debate de ideias de forma positiva e enriquecedora. Contribuir também para a análise de erros/dificuldades e valorizar as diferentes resoluções.
Encerramento

Tempo Sugerido: 2 minutos
Orientação: Faça o fechamento da atividade principal retomando brevemente com os alunos o que foi necessário para descobrir o total de contas do colar de Bruna, ou seja, a utilização do que já aprenderam sobre as diversas sequências numéricas. Como a sua utilização facilita a contagem e a torna mais rápida.
Propósito: Retomar a ideia de que existem diferentes formas de sequenciar quantidades.
Raio x
Tempo sugerido: 6 minutos (Slides 11 e 12)
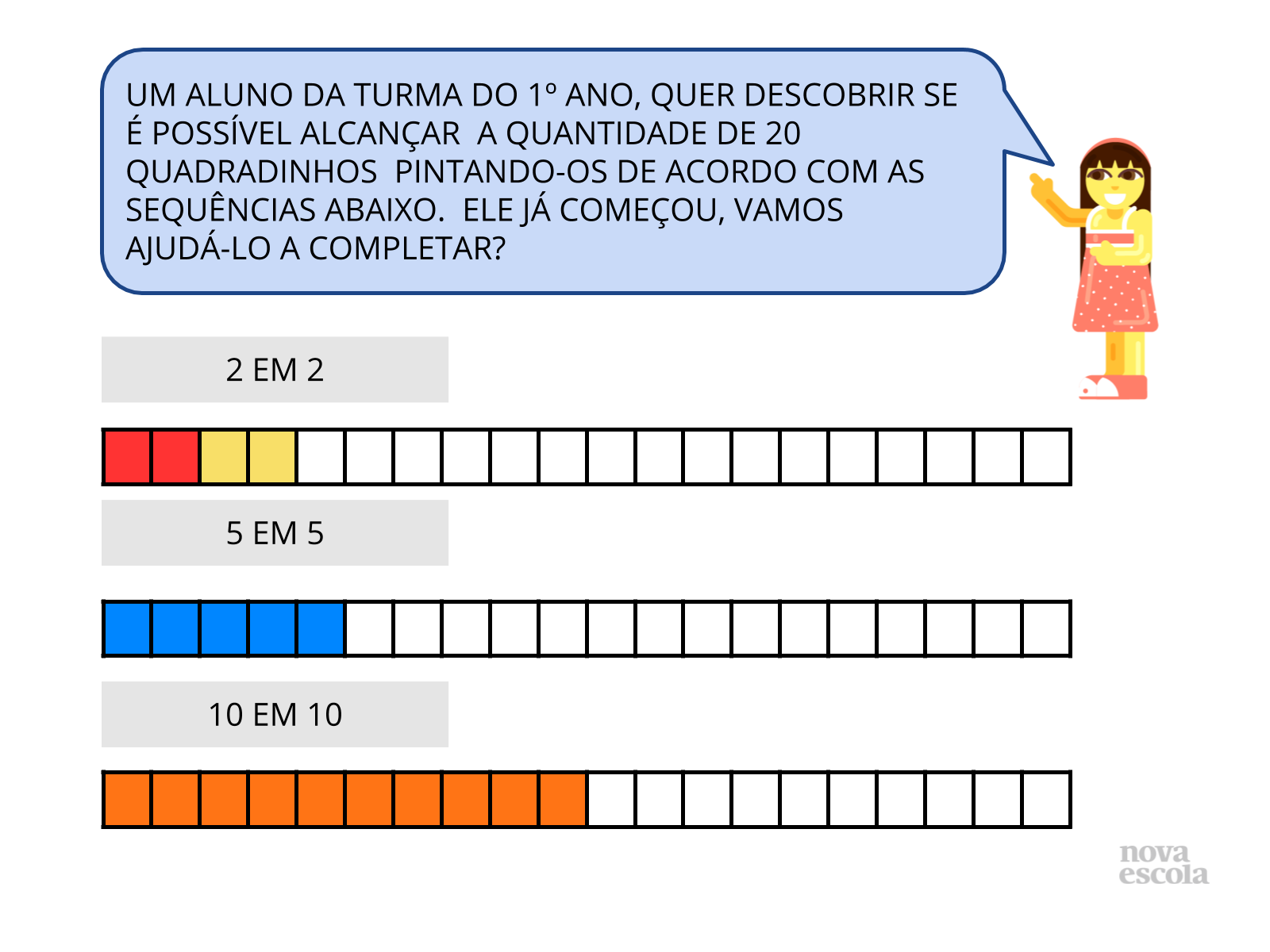
Orientação: Entregue uma cópia da atividade para cada aluno. Leia a situação problema e reserve um tempo para que possam analisar e encontrar uma forma de resolvê-la sozinhos. O raio x é uma atividade oportuna para verificar e avaliar se os alunos conseguiram compreenderam o conteúdo proposto e alcançar o objetivo de aprendizagem.
Propósito: Auxiliar o aluno a perceber possíveis relações entre as sequências numéricas de acordo com determinada quantidade.
Discuta com a turma:
- Como é possível alcançar o total de 20 quadradinhos em cada sequência?
- O que será necessário fazer?
Materiais complementares:
Raio X
Resolução do raio x
Atividade complementar
Resolução da atividade complementar
Raio x
Tempo sugerido: 2minutos
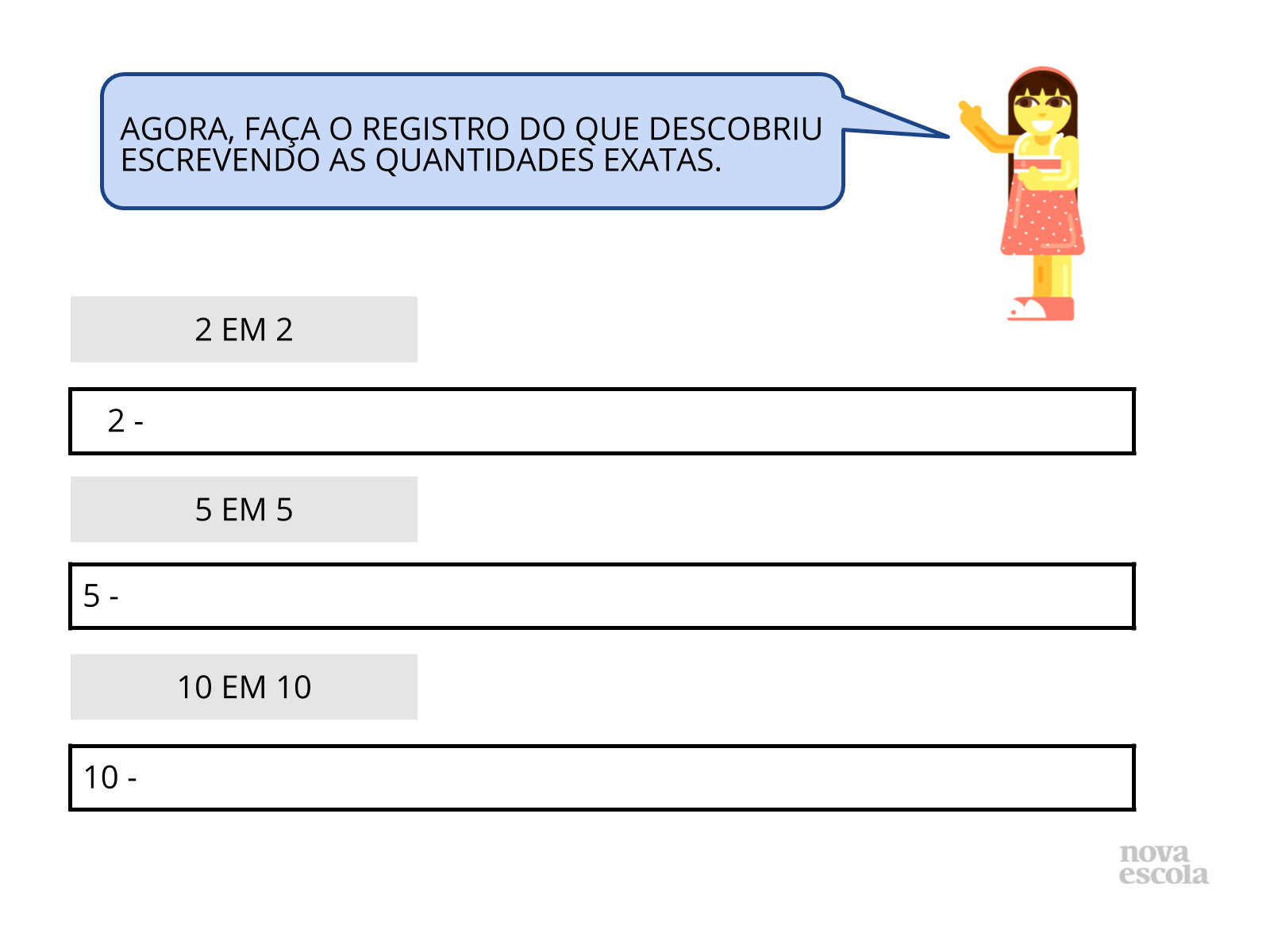
Orientação: Entregue uma cópia da atividade para cada aluno. Leia a situação problema e reserve um tempo para que possam analisar e encontrar uma forma de resolvê-la sozinhos. O raio x é uma atividade oportuna para verificar e avaliar se os alunos conseguiram compreenderam o conteúdo proposto e alcançar o objetivo de aprendizagem.
Propósito: Auxiliar o aluno a perceber possíveis relações entre as sequências numéricas de acordo com determinada quantidade.
Discuta com a turma:
- A quantidade de 20 quadradinhos pôde ser distribuída nas três formas de sequências?
- O valor exato foi alcançado ao final dessa distribuição?
- Qual das três sequências, obteve maior número de distribuições? Por quê?
- Qual teve menos distribuições? Por quê?
Materiais complementares:
Raio X
Resolução do raio x
Atividade complementar
Resolução da atividade complementar




























