Resumo da Aula
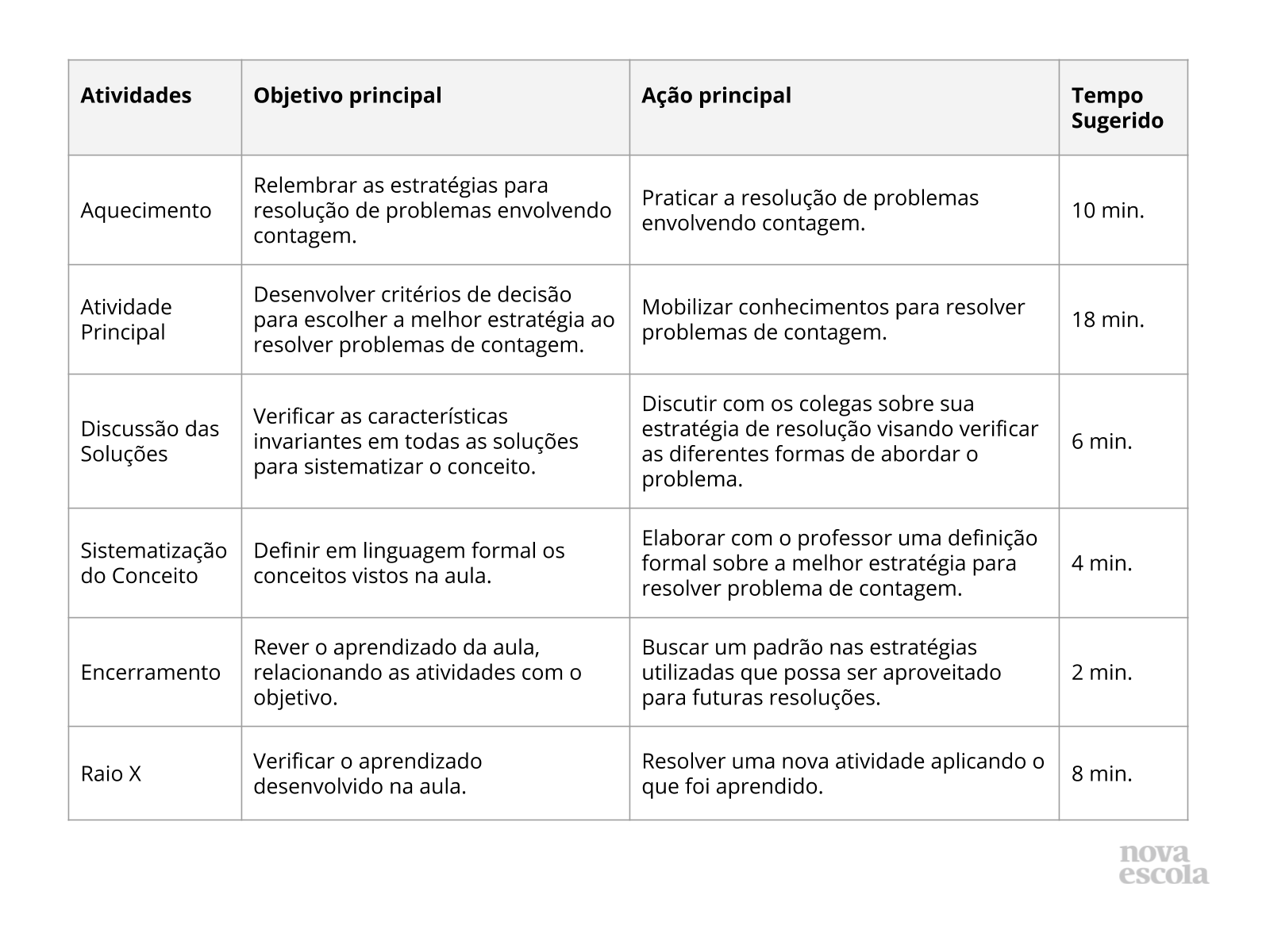
Objetivo

Tempo sugerido: 2 minutos.
Orientações: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada
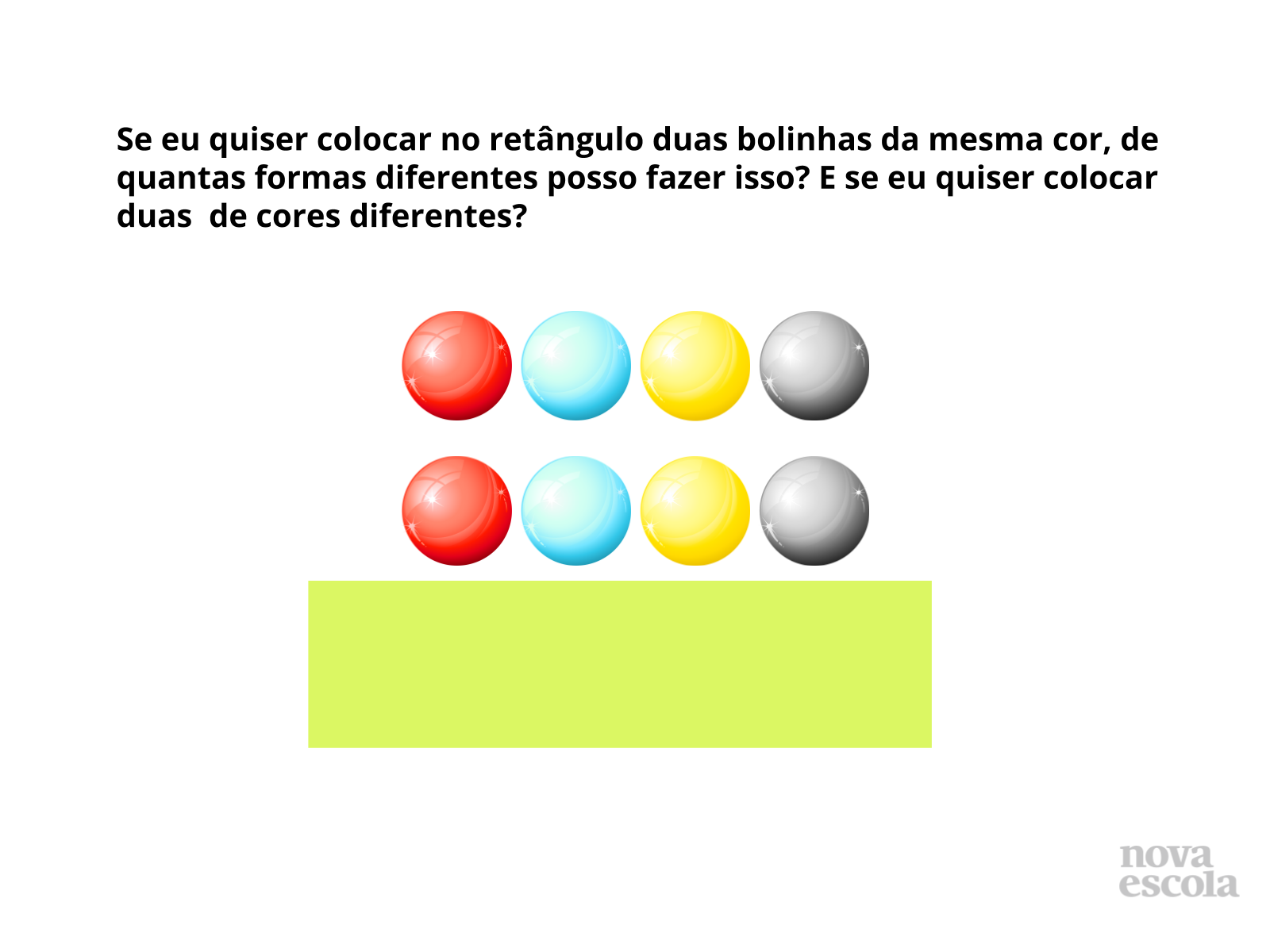
Tempo sugerido: 10 minutos.
Orientações: Prepare o material manipulativo antes da aula. Você pode imprimir este modelo ou criar um novo usando cartolina ou outro papel. Reforce para a turma o conceito de combinação e veja se todos os alunos já possuem conhecimentos acerca deste tema. Se certifique que todos compreenderam bem o enunciado e faça um levantamento sobre o conhecimento dos alunos acerca das estratégias que eles conhecem para solucionar este tipo de problema, assim observe se o nível de conhecimento está equalizado. Dê atenção a todos os alunos para que nenhum fique de fora do processo de ensino-aprendizagem. Incentive a interação entre a turma de maneira que, os alunos com mais facilidade em resolver o problema, possam ajudar aos que estão com dificuldade. Oriente que esta atividade requer bastante atenção.
Propósito: Promover a familiaridade com o material manipulativo, compreender que a partir da interação entre os alunos é possível dinamizar o processo de ensino-aprendizagem e estudar formas de contagem de possibilidades.
Discuta com a Turma:
- O que o problema pede?
- Quantas combinações diferentes é possível fazer?
- Vocês podem explicar o que significa combinação?
- Qual a melhor estratégia para resolver este problema?
- É possível resolver este problema de uma outra forma?
- Quais são as dificuldades comuns da turma neste problema?
- Se houvesse mais cores e mais bolinhas, seria possível resolver da mesma forma?
Materiais complementares para impressão:
Aquecimento
Resolução do aquecimento
Atividade Principal
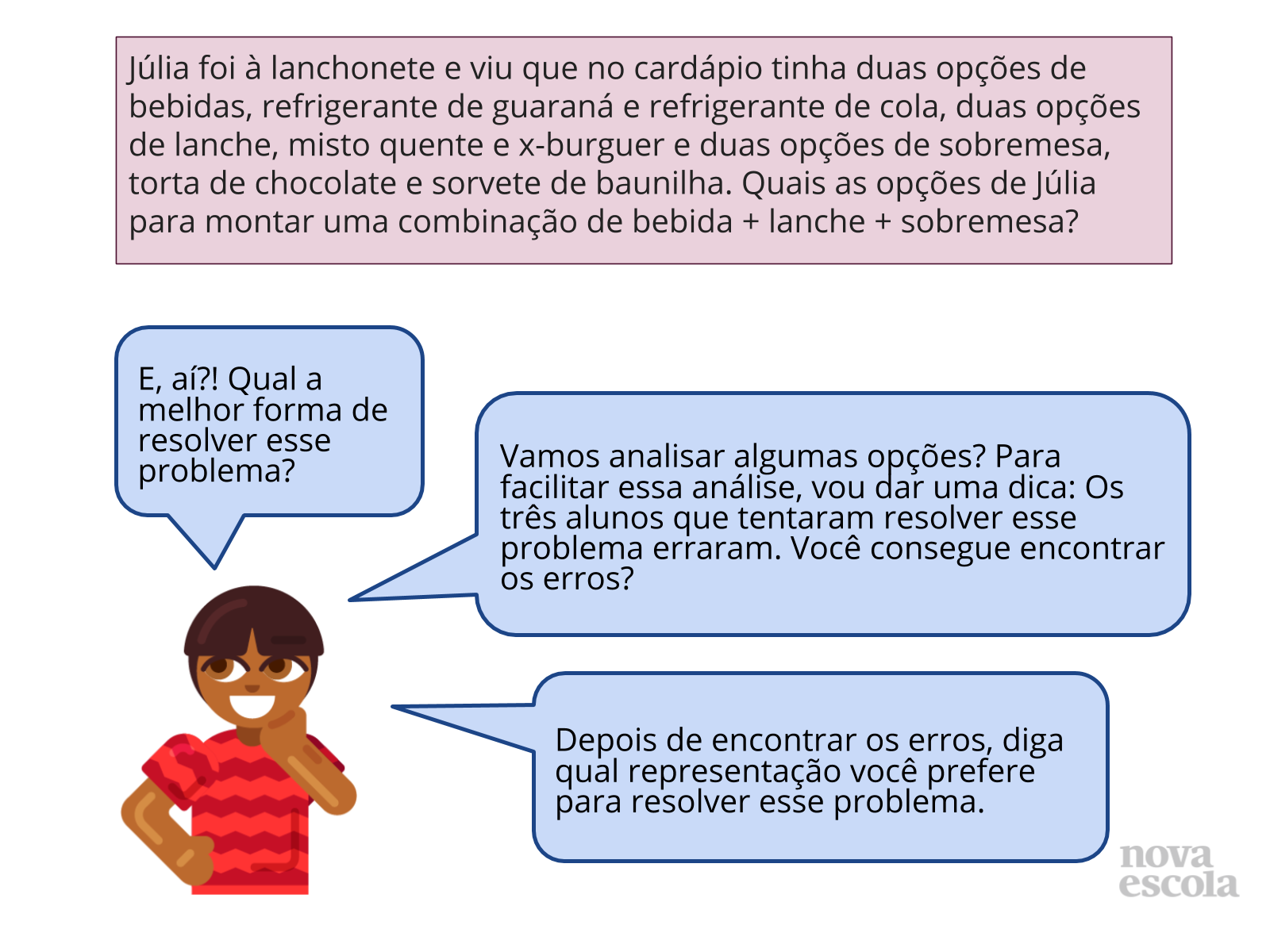
Tempo sugerido: 18 minutos. (Slides 4 a 6).
Orientações: Você poderá escrever o texto do problema no quadro, projetá-lo ou entregar uma cópia aos alunos. Explique aos alunos que eles devem utilizar os conhecimentos e estratégias que já conhecem para solucionar o problema. Deixe que os estudantes leiam o problema e dê algum tempo para que tentem resolvê-lo. Não faça nenhuma intervenção neste momento, observe como os alunos analisam os dados do problema, interpretam e elaboram suas estratégias. Após um certo tempo, mesmo que os alunos não tenham terminado suas próprias resoluções, apresente os slides 5 e 6 pedindo que os alunos encontrem o erro em cada resolução, justificando por que está errada. Espera-se que os alunos comparem as resoluções com seus raciocínios iniciais, completando sua própria resposta e encontrando o erro apresentado no slide.
Propósito: Fazer com que os alunos mobilizem os conhecimentos que já possuem para resolver o problema e dinamizar a aula para uma melhor interação dos alunos.
Discuta com a Turma:
- Por onde devemos começar para resolver o problema?
- Quais são as informações que o aluno deve dar mais atenção para resolver este problema?
- É possível resolver este problema através de uma estratégia de cálculo?
- Qual a melhor maneira de resolver?
- Todos os métodos de resolução apresentados são bons? Qual a dificuldade de cada método?
Materiais complementares para impressão:
Atividade principal
Resolução da atividade principal
Guia de intervenção
Atividade Principal
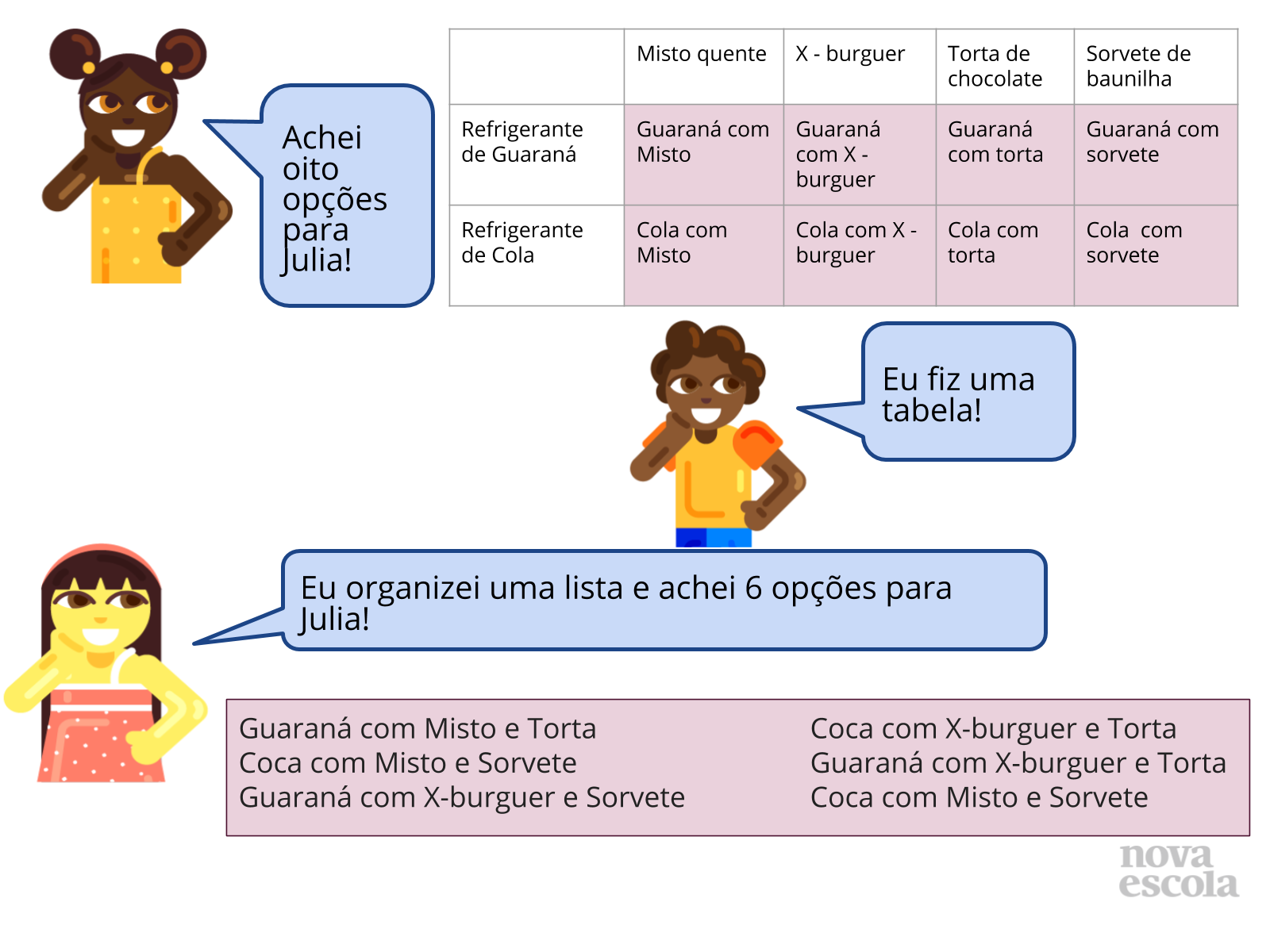
Tempo sugerido: 18 minutos. (Slides 4 a 6).
Orientações: Você poderá escrever o texto do problema no quadro, projetá-lo ou entregar uma cópia aos alunos. Explique aos alunos que eles devem utilizar os conhecimentos e estratégias que já conhecem para solucionar o problema. Deixe que os estudantes leiam o problema e dê algum tempo para que tentem resolvê-lo. Não faça nenhuma intervenção neste momento, observe como os alunos analisam os dados do problema, interpretam e elaboram suas estratégias. Após um certo tempo, mesmo que os alunos não tenham terminado suas próprias resoluções, apresente os slides 5 e 6 pedindo que os alunos encontrem o erro em cada resolução, justificando por que está errada. Espera-se que os alunos comparem as resoluções com seus raciocínios iniciais, completando sua própria resposta e encontrando o erro apresentado no slide.
Propósito: Fazer com que os alunos mobilizem os conhecimentos que já possuem para resolver o problema e dinamizar a aula para uma melhor interação dos alunos.
Discuta com a Turma:
- Por onde devemos começar para resolver o problema?
- Quais são as informações que o aluno deve dar mais atenção para resolver este problema?
- É possível resolver este problema através de uma estratégia de cálculo?
- Qual a melhor maneira de resolver?
- Todos os métodos de resolução apresentados são bons? Qual a dificuldade de cada método?
Atividade Principal
Tempo sugerido: 18 minutos. (Slides 4 a 6).
Orientações: Você poderá escrever o texto do problema no quadro, projetá-lo ou entregar uma cópia aos alunos. Explique aos alunos que eles devem utilizar os conhecimentos e estratégias que já conhecem para solucionar o problema. Deixe que os estudantes leiam o problema e dê algum tempo para que tentem resolvê-lo. Não faça nenhuma intervenção neste momento, observe como os alunos analisam os dados do problema, interpretam e elaboram suas estratégias. Após um certo tempo, mesmo que os alunos não tenham terminado suas próprias resoluções, apresente os slides 5 e 6 pedindo que os alunos encontrem o erro em cada resolução, justificando por que está errada. Espera-se que os alunos comparem as resoluções com seus raciocínios iniciais, completando sua própria resposta e encontrando o erro apresentado no slide.
Propósito: Fazer com que os alunos mobilizem os conhecimentos que já possuem para resolver o problema e dinamizar a aula para uma melhor interação dos alunos.
Discuta com a Turma:
- Por onde devemos começar para resolver o problema?
- Quais são as informações que o aluno deve dar mais atenção para resolver este problema?
- É possível resolver este problema através de uma estratégia de cálculo?
- Qual a melhor maneira de resolver?
- Todos os métodos de resolução apresentados são bons? Qual a dificuldade de cada método?
Discussão das Soluções
Tempo sugerido: 6 minutos.
Orientações: Observe se algum aluno não conseguiu resolver a atividade. Peça para algum deles apresentar a estratégia utilizada para resolver a atividade, caso algum outro aluno tenha resolvido de maneira diferente, peça qu ele apresente para a turma esta outra estratégia. tente, ao máximo, fazer com que todos os alunos participem deste momento da aula. Se por acaso, algum aluno não conseguiu resolver, solicite que outro colega que teve facilidade na resolução, ajude-o. Analise diferentes operações (ou seja, com alunos que resolveram por caminhos distintos), para que todos percebam que em qualquer caso o raciocínio combinatório permanece. Discuta com os alunos sobre os erros dados nas respostas dos slides anteriores.
Propósito: Realizar um fechamento das ideias discutidas até o momento e discutir alternativas diferentes de resolução.
Discuta com a Turma:
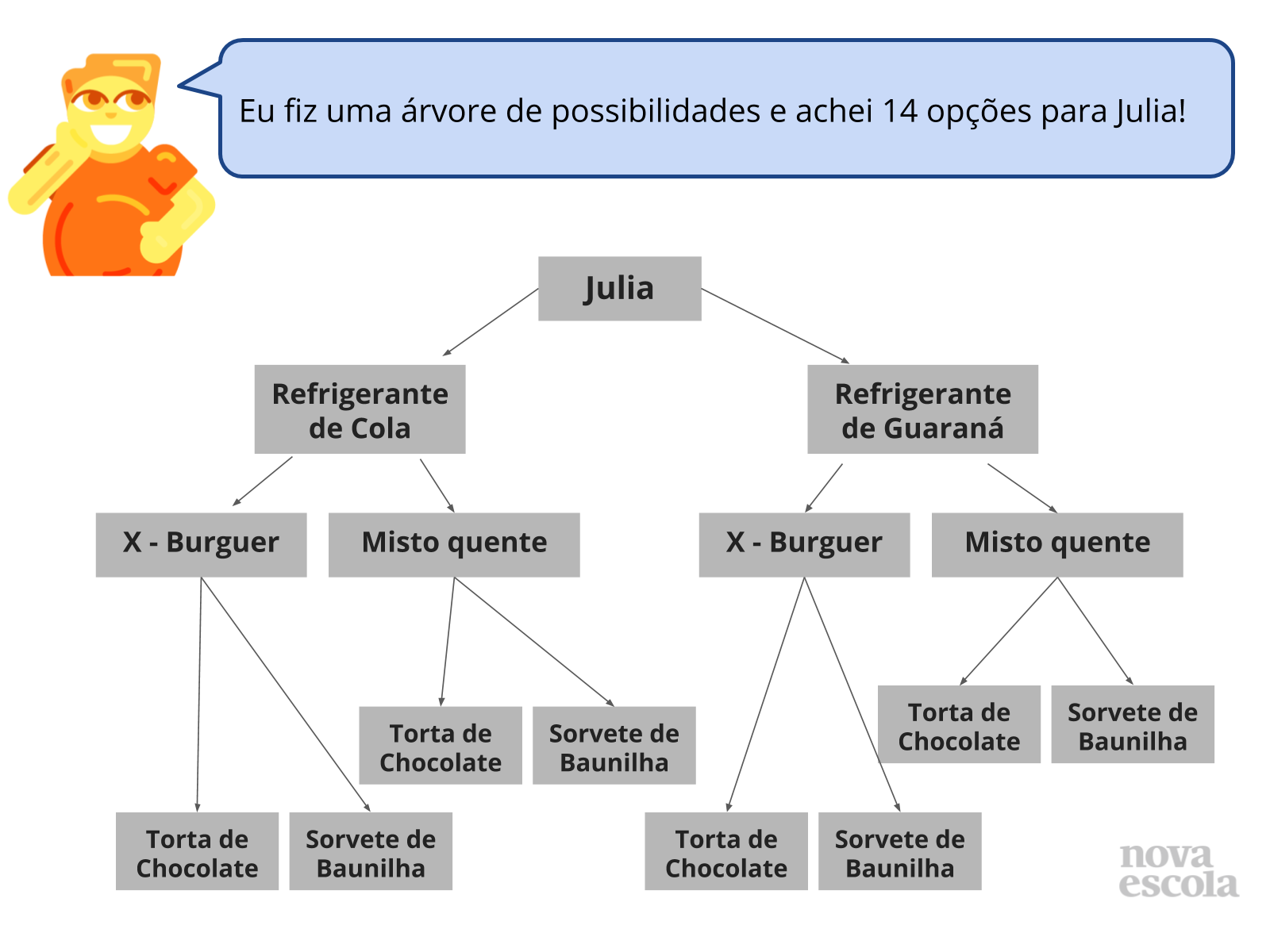
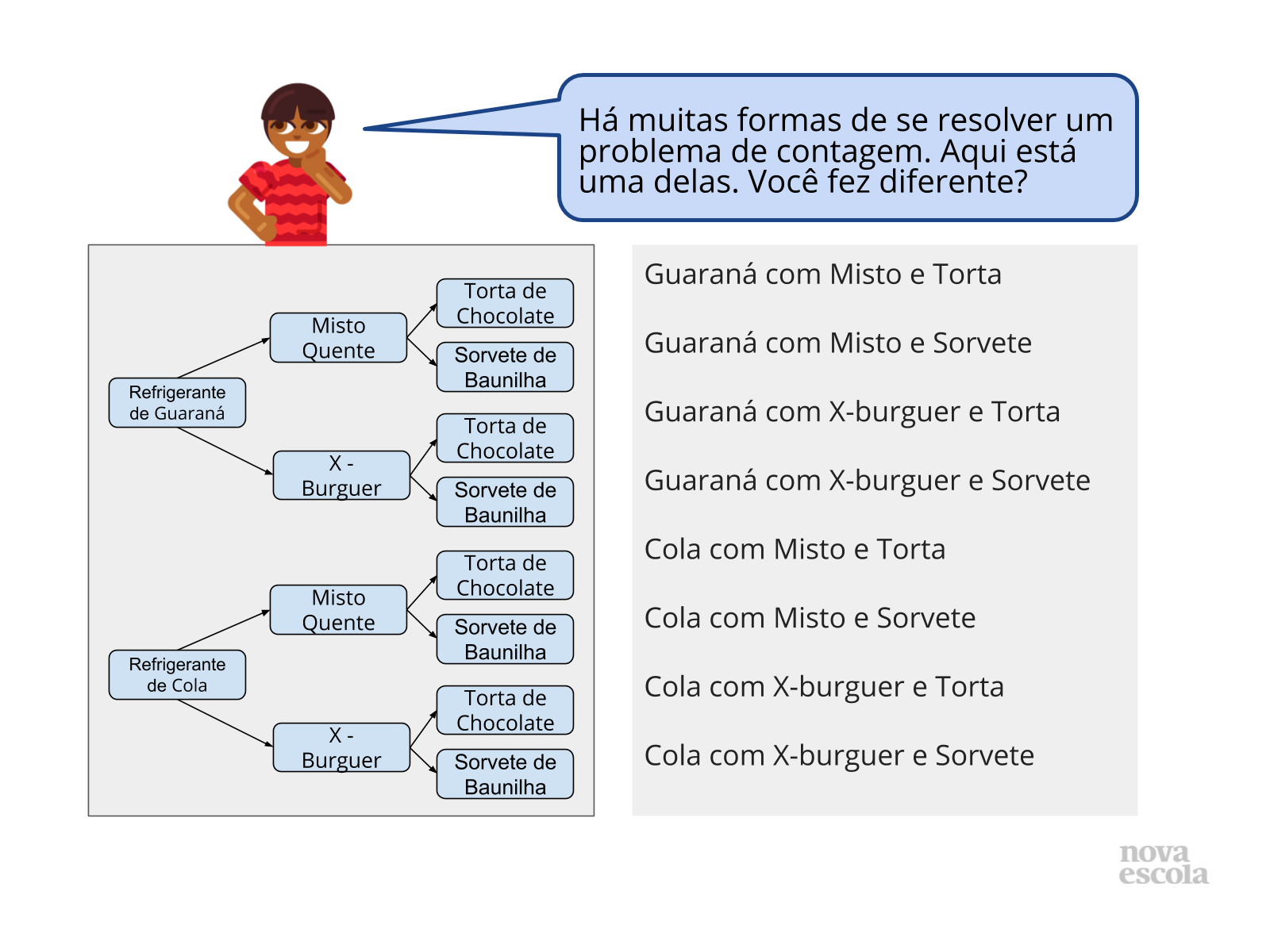
- Como você pode usar a árvore de possibilidades para montar a lista de respostas possíveis para a escolha de Julia?
Sistematização do Conceito

Tempo sugerido: 4 minutos.
Orientações: Encerre a atividade retomando com os alunos o processo de escolha de melhor estratégia para a resolução do problema.
Propósito: Aprofundar um pouco mais o conceito relacionado à Atividade Principal.
Discuta com a Turma:
- O método de ir listando os possíveis resultados deve seguir um padrão muito claro, mas ainda assim é muito fácil confundir e esquecer alguma resposta ou contar alguma resposta duas vezes, ou seja, discuta com a turma, qual a necessidade de ter muita atenção na hora de listar as possibilidades?
Encerramento

Tempo sugerido: 2 minutos.
Orientações: Encerre a atividade apresentando aos alunos como, através da escolha correta de resolução, resolver problemas de contagem pode ser objetivo.
Propósito: Sistematizar os conhecimentos adquiridos na aula.
Discuta com a Turma:
- A atividade auxiliou na sua compreensão do conceito de porcentagem?
Raio X
Tempo sugerido: 8 minutos.
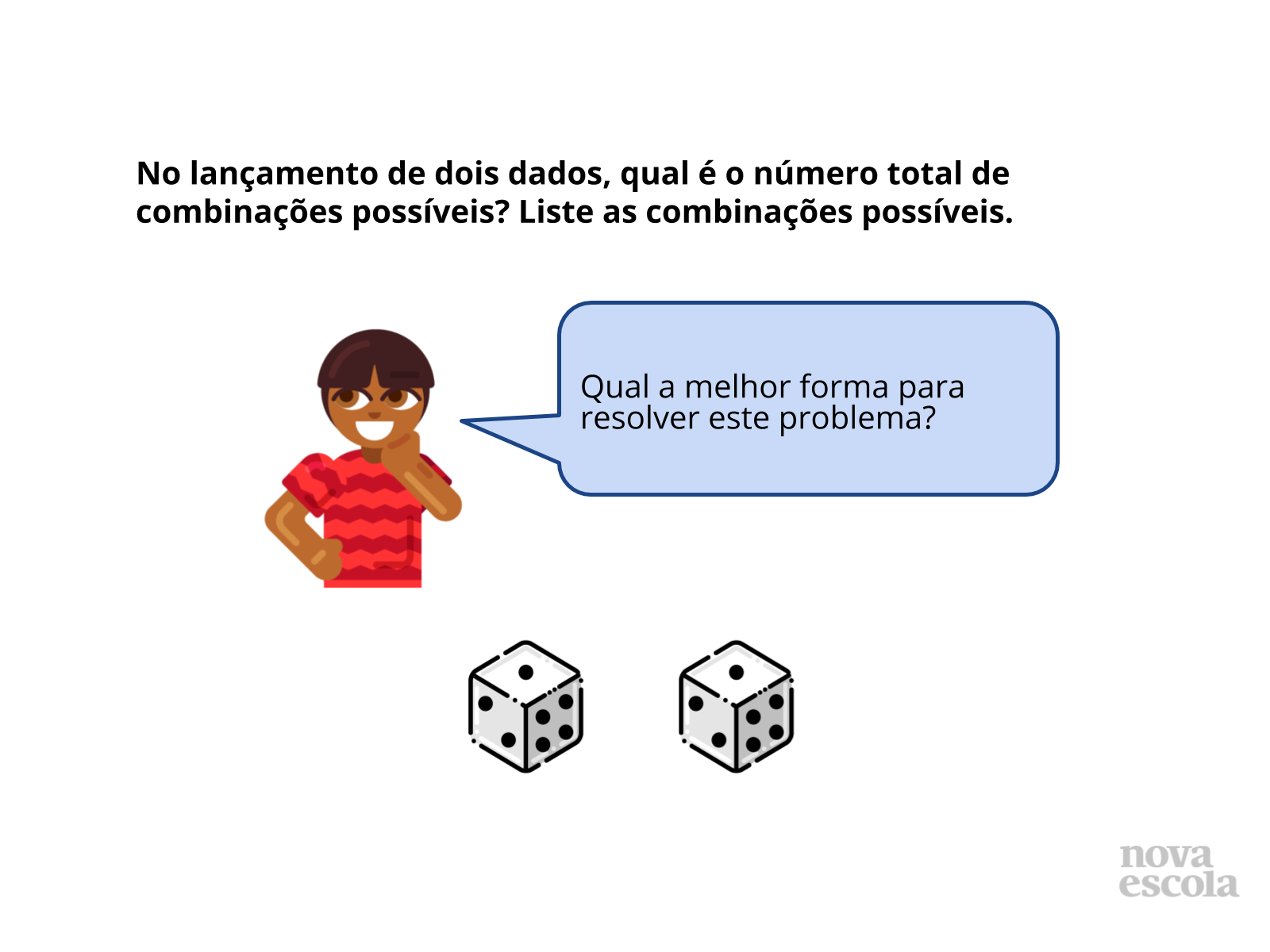
Orientações: Apresente a nova situação e peça que os alunos digam em voz alta alguns caminhos que podem seguir para resolvê-la. Você pode projetar, passar no quadro ou fazer cópia para os alunos. O Raio X é um momento para você avaliar se todos os alunos conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. Mostre alguns exemplos do que se está querendo dizer aqui com combinação, por exemplo, mostrando que, se sair 2 na face superior de um dado e 5 na face superior do outro, podemos montar os pares 2 e 5 ou 5 e 2.
Propósito: Deixar que o processo de ensino-aprendizagem ocorra através da maior interação que esta atividade propõe entre aluno e professor. Auxiliar os alunos a perceberem que todas as estratégias de resolução de problemas são válidas e o mais importante é elaborar uma estratégia consistente e conseguir justificá-la matematicamente. Por fim, verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante e avaliar os conhecimentos de cada um a respeito da relação entre algumas porcentagens e suas frações equivalentes.
Discuta com a Turma:
- Depois de tudo o que vimos nesta aula, qual a forma mais prática para resolver este problema?
- Quantos números de dois algarismos posso formar com o 5 e o 2? E se sair 1 e 1 nos dois dados, quantos números consigo formar?
Materiais complementares para impressão:
Raio X
Resolução do raio x
Atividade complementar
Resolução da atividade complementar





















