Guia de Intervenção
Plano de Aula
Plano de aula: Fração Geratriz de Dízima Periódica Composta
Plano 7 de uma sequência de 10 planos. Veja todos os planos sobre Números decimais exatos, dízimas periódicas e frações
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Juliana Malta de Sousa
Mentor: Amanda Ferreira Verardo Bilia
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF08MA05 - Reconhecer e utilizar procedimentos para a obtenção de uma fração geratriz para uma dízima periódica.
Objetivos específicos
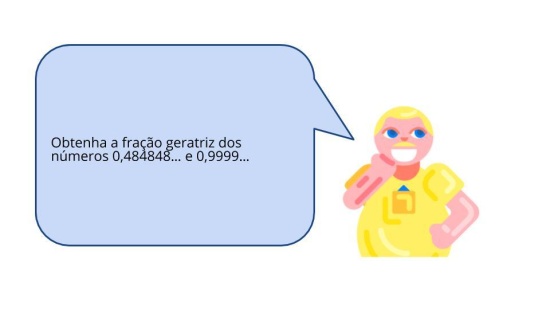
Obter a fração geratriz de dízimas periódicas compostas.
Conhecimentos prévios
Resolver equação de primeiro grau e simplificar frações.
Conceito-chave
Fração geratriz, dizima periódica simples e composta.
Recursos necessários
- Folha de papel A4 branca
- calculadora
- atividades impressas
Habilidades BNCC:
Objetivos de aprendizagem
Obter a fração geratriz de dízimas periódicas compostas.
Resumo da aula
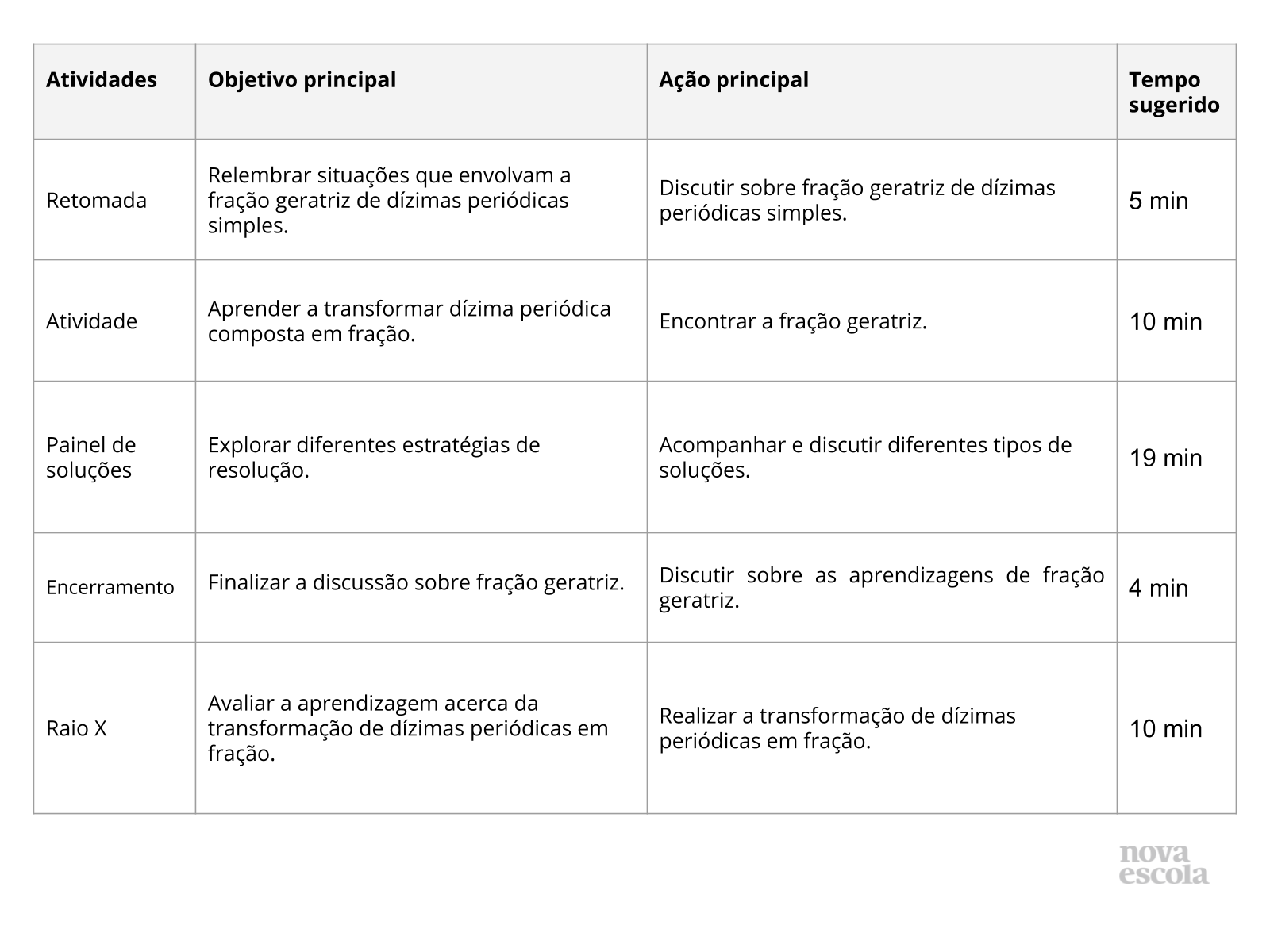 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 min.
Orientação: Projete, escreva na lousa ou leia o objetivo para turma. Peça para os alunos citar alguns exemplos de dízimas periódicas e peça para eles encontrarem suas frações geratrizes.
Propósito: Ensinar os alunos a encontrar a fração geratriz de uma dízima periódica simples e composta.
Retomada

Tempo sugerido: 5 minutos (slides 3 e 4)
Orientação: Você poderá escrever o texto do problema no quadro, projetá-lo ou entregar uma cópia aos alunos. Coloque os alunos em duplas ou trios e dê tempo para que tentem resolvê-lo junto com um colega. Não faça nenhuma intervenção neste momento, circule pela sala e observe como os alunos analisam os dados do problema, interpretam e elaboram suas estratégias, nesse momento encoraje os alunos e proponha alguns questionamentos.
Propósito: Fazer com que os alunos mobilizem os conhecimentos que já possuem de dízimas periódicas simples para solucionar o problema dado.
Discuta com a turma:
- O que vocês entendem por fração irredutível? Dê alguns exemplos.
- Qual o período de cada dízima apresentada na expressão numérica?
- Qual a classificação dessas dízimas? Por quê?
- Como transforma essas dízimas em fração?
Materiais complementares:
Retomada
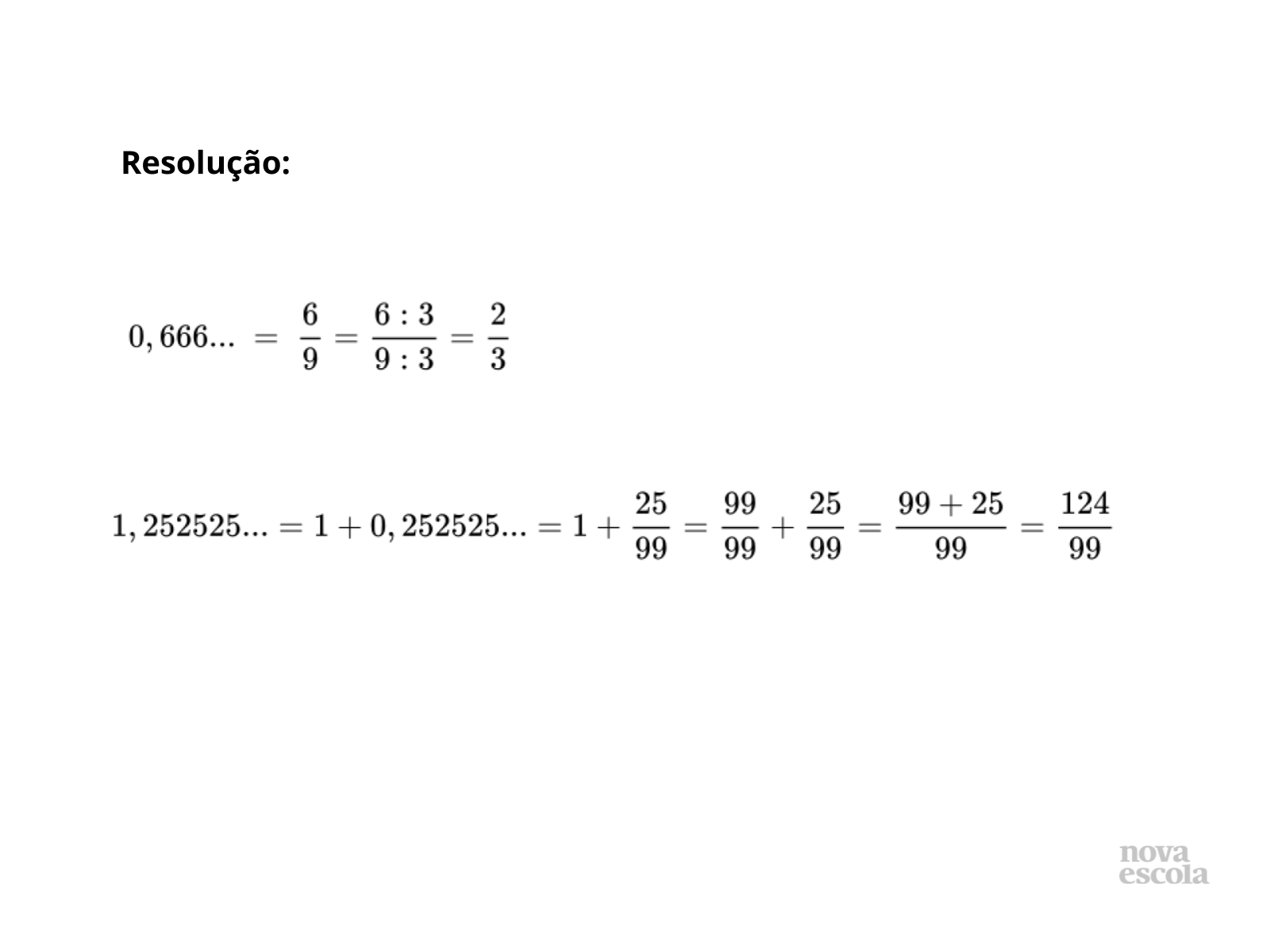
Tempo sugerido: 5 minutos (slide 3 e 4)
Orientações: No momento da correção deixe os alunos apresentarem suas resoluções, convide-os para resolver na lousa, verifique se alguém resolveu diferente e solicite também para ir na lousa, chame inclusive alunos que resolveram só uma parte ou que resolveram o exercício de maneira errada. Deixe que os alunos percebam e validem as respostas dos colegas e percebam qual resolução é mais vantajosa. Se os alunos não resolverem o problema, leve-os a identificar a dificuldade. Peça para resolverem com o auxílio uma equação também. Na hora da prova real peça para os alunos usarem a calculadora para conferir a fração encontrada.
Propósito: Explorar várias estratégias de resolução.
Discuta com a turma:
- Podemos simplificar a fração 6/9? Por qual número?
- Como provar que ? é a resposta correta?
- Podemos separar a parte inteira da parte decimal do número 1,252525…?
- Como podemos somar número inteiro com fração?
- Qual a fração equivalente a 1 inteiro com o denominador 99?
- Como provar que 124/99 é a resposta correta?
Materiais complementares:
Atividade Principal

Tempo sugerido: 10 minutos (slide 5 e 9)
Orientação: Você poderá escrever o texto do problema no quadro, projetá-lo ou entregar uma cópia aos alunos. Faça uma discussão coletiva, com todos os alunos, pois é uma ampliação de conteúdo e no começo poderá surgir dúvidas. Inicie com os questionamentos e vá por meio de perguntas concluindo parte por parte.
Propósito: Fazer com que os alunos mobilizem os conhecimentos que já possuem de dízimas periódicas simples e composta para solucionar o problema sobre fração geratriz.
Discuta com a turma:
- Qual o período de cada dízima periódica?
- Qual a classificação dessas dízimas?
- Como podemos transformar 0,4555… em fração?
- A regra é a mesma para 0,555…? Façam tentativas. Por qual número devo multiplicar para eliminar a dízima periódica?
Materiais complementares:
Resolução da Atividade Principal
Acesse aqui o guia de intervenções para discutir as possíveis dificuldades dos alunos.
Discussão da solução

Tempo sugerido: 19 minutos (slide 6 à 8 ).
Orientações: Professor conduza os alunos a discutir as soluções por caminhos diferentes para a situação dada. Não basta estar certo, tem que pensar de um outro jeito. Não basta acabar primeiro, tem que continuar, colaborar, criar, levar os pensamentos a uma mentalidade matemática de crescimento. Resolva o exercício de formas diversas, pois resolvendo de uma única forma dimimui a riqueza da discussão e da compreensão do conceito estudado. Inicie fazendo os questionamentos, convide alguns alunos para expor sua resolução na lousa, ou o seu raciocínio, ou sua estratégia, após algumas resoluções diferentes peça para os alunos explicar como pensaram em resolver cada parte, verifique as semelhanças e diferenças de uma transformação em fração de uma dízima simples e uma dízima composta, no final é interessante deixar que a sala possa validar em certo ou errado junto com o professor. Não projete as soluções acima antes dos alunos tentarem mostrar suas resoluções, sempre pergunte se alguém resolveu diferente e convide para ir na lousa, chame também na lousa alunos que resolveram errado para que a sala possa tentar ajudar a descobrir o erro e o aluno possa perceber como finalizar o exercício. Após mostrar várias resoluções mostre qual é mais vantajosa e pode ser usada em qualquer problema. Na hora de fazer a prova real deixe os alunos usarem a calculadora.
Propósito: Explorar diversas formas de resolução para uma mesma situação problema.
Discuta com a turma:
- Como transformamos 0,4555... em fração? A dízima é simples ou composta? Qual o período dessa dízima?
- Podemos transformar em fração as dízimas periódicas compostas numa equação de primeiro grau igual as dízimas periódicas simples?
- Em uma equação o que o sinal de igual significa? Como resolvemos uma equação de primeiro grau?
- Por qual número devemos multiplicar para deixar a parte não periódica para antes da vírgula?
- Por qual número devemos multiplicar para deixar o período da dízima antes da vírgula?
- Posso simplificar a fração 41/90?
- Qual a semelhança e diferença no processo de transformação em fração de uma dízima periódica simples para uma composta?
Materiais complementares.
Discussão da solução

Tempo sugerido: 19 minutos (slide 6 à 8 ).
Orientações: Professor conduza os alunos a discutir as soluções por caminhos diferentes para a situação dada. Não basta estar certo, tem que pensar de um outro jeito. Não basta acabar primeiro, tem que continuar, colaborar, criar, levar os pensamentos a uma mentalidade matemática de crescimento. Resolva o exercício de formas diversas, pois resolvendo de uma única forma diminui a riqueza da discussão e da compreensão do conceito estudado. Inicie fazendo os questionamentos, convide alguns alunos para expor sua resolução na lousa, ou o seu raciocínio, ou sua estratégia, após algumas resoluções diferentes é interessante deixar que a sala possa validar em certo ou errado junto com o professor. Não projete as soluções acima antes dos alunos tentarem mostrar suas resoluções, sempre pergunte se alguém resolveu diferente e convide para ir na lousa, chame também na lousa alunos que resolveram errado para que a sala possa tentar ajudar a descobrir o erro e o aluno possa perceber como finalizar o exercício. Após mostrar várias resoluções mostre qual é mais vantajosa e pode ser usada em qualquer problema. Na hora de fazer a prova real deixe os alunos usarem a calculadora.
Propósito: Explorar diversas formas de resolução para uma mesma situação problema.
Discuta com a turma:
- Qual a diferença dessa dízima com a anterior?
- A dízima 0,25888… é simples ou composta? Qual o período dessa dízima? Como que transforma essa dízima em fração?
- Por qual número devemos multiplicar 0,25888… para deixar o período da dízima antes da vírgula?
- Podemos subtrair 258,888... de 0,25888…? Mas conseguimos eliminar a parte periódica? O que devemos fazer para eliminar a parte periódica?
- A fração 233/900 pode ser simplificada?
- Como se consegue provar que 233/900 é a resposta certa?
- Qual a diferença na transformação de fração da dízima periódica simples para a composta?
Discussão da solução

Tempo sugerido: 19 minutos (slide 6 à 8 ).
Orientações: Professor conduza os alunos a discutir as soluções por caminhos diferentes para a situação dada. Não basta estar certo, tem que pensar de um outro jeito. Não basta acabar primeiro, tem que continuar, colaborar, criar, levar os pensamentos a uma mentalidade matemática de crescimento. Resolva o exercício de formas diversas, pois resolvendo de uma única forma diminui a riqueza da discussão e da compreensão do conceito estudado. Inicie fazendo os questionamentos, convide alguns alunos para expor sua resolução na lousa, ou o seu raciocínio, ou sua estratégia, após algumas resoluções diferentes é interessante deixar que a sala possa validar em certo ou errado junto com o professor. Não projete as soluções acima antes dos alunos tentarem mostrar suas resoluções, sempre pergunte se alguém resolveu diferente e convide para ir na lousa, chame também na lousa alunos que resolveram errado para que a sala possa tentar ajudar a descobrir o erro e o aluno possa perceber como finalizar o exercício. Após mostrar várias resoluções mostre qual é mais vantajosa e pode ser usada em qualquer problema. Na hora de fazer a prova real deixe os alunos usarem a calculadora.
Propósito: Explorar diversas formas de resolução para uma mesma situação problema.
Discuta com a turma:
- Qual a diferença dessa dízima para a anterior?
- A dízima 0,3565656… é simples ou composta? Qual o período dessa dízima? Como que transforma essa dízima em fração?
- Por qual número devemos multiplicar para deixar o período da dízima antes da vírgula?
- A fração 353/990 pode ser simplificada?
- Como se consegue provar que 353/990 é a resposta certa?
- Qual a diferença na transformação de fração da dízima periódica simples para a composta?
- Podemos criar uma regra direta para transformar uma dízima periódica composta em fração?
Atividade Principal

Tempo sugerido: 10 minutos (slide 5 e 9)
Orientação: Você poderá escrever o texto do problema no quadro, projetá-lo ou entregar uma cópia aos alunos. Faça uma discussão coletiva, com todos os alunos, pois é uma ampliação de conteúdo e no início poderá surgir dúvidas. Inicie com os questionamentos e vá por meio de perguntas concluindo parte por parte.
Propósito: Fazer com que os alunos mobilizem os conhecimentos que já possuem de dízimas periódicas simples e composta para solucionar o problema sobre fração geratriz.
Discuta com a turma:
- Qual o período de cada dízima periódica?
- Qual a classificação dessas dízimas?
- Como podemos transformar essa dízima em fração?
- A regra é a mesma para dízimas diferentes? Façam tentativas. Por qual número devemos multiplicar para eliminar a dízima periódica?
Materiais complementares:
Encerramento

Tempo sugerido: 4 minutos.
Orientações: Apresente o slide ou escreva na lousa encerrando a atividade.
Propósito: Generalizar a transformação de dízima periódica composta em fração.
Discuta com a turma:
Neste momento da aula você pode utilizar perguntas reflexivas, como por exemplo:
- Como você ou seu grupo abordou o problema ou conjunto de problemas de hoje? Sua abordagem foi bem-sucedida? O que você aprendeu com sua abordagem?
- Quais foram os principais conceitos ou ideias matemáticas que você aprendeu hoje ou que discutimos em aula hoje?
- Você ainda tem alguma dúvida? Caso você não tenha dúvida, escreva um problema semelhante e resolva-o.
- Descreva um erro ou conceito errôneo que você ou um colega apresentou na aula de hoje. O que você aprendeu com esse erro ou conceito errôneo?
- Descreva detalhadamente como outro aluno da turma abordou o problema. Em que aspecto tal abordagem se assemelha ou difere da maneira como você abordou o problema?
- Quais novas palavras ou denominações foram apresentadas hoje? O que você acha que cada palavra significa? Apresente um exemplo/uma imagem de cada palavra.
- O que se manteve como você pensava? O que mudou?
- O que aconteceria se você mudasse algum aspecto?
- Quais foram seus pontos fortes e fracos, nesta aula? Qual é o seu plano para melhorar nas áreas em que teve dúvida?
- Você conseguiria fazer uma representação visual para responder o problema?
Outra opção é deixar algumas dessas questões como tarefa de casa, podem trazer benefícios tanto quanto exercícios que exigem cálculos.
Essas perguntas e outras ideias relacionadas a mentalidades matemáticas de crescimento você pode encontrar no livro Mentalidades Matemáticas: estimulando o potencial dos estudantes por meio da matemática criativa, das mensagens inspiradoras e do ensino inovador, de Jo Boaler, Editora Penso.
Raio X

Tempo sugerido: 10 minutos.
Orientações: Peça que, individualmente, os alunos leiam a atividade e a realizem. Circule pela sala para verificar como os alunos estão respondendo. O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários, dúvidas ou dificuldade de cada um. No final, reserve um tempo para um debate coletivo registrando as soluções na lousa. Você pode fazer o download desta atividade para imprimir para os seus alunos aqui.
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante e avaliar os conhecimentos de cada um a respeito da fração geratriz de dízimas simples e compostas.
Acesse aqui a resolução dessa atividade.
Discuta com a turma:
- É fácil encontrar a fração geratriz de um número racional?
- Tem algum caso mais simples de fração geratriz e outros mais complexos? Cite exemplos e explique o porquê?
Materiais complementares:
Resolução da Atividade Complementar
Resolução da Atividade de Raio X
Sugestão de adaptação para ensino remoto
Professor, revisite todos os arquivos do plano que você vai orientar e identifique os pontos principais para o trabalho remoto. Lembre-se que as sugestões precisam envolver tanto o uso da tecnologia quanto situações em que a tecnologia não está disponível.
Recursos
USAR APENAS FERRAMENTAS EM PORTUGUÊS E GRATUITAS.
- Necessários: papel, lápis, calculadora.
- Opcionais: Meet, Hangout, Whatsapp, plataforma da Khan Academy (disponível aqui).
Para este plano, foque na etapa ATIVIDADE PRINCIPAL.
Aquecimento
Pode ser suprimido para dar atenção à Atividade Principal.
Atividade principal
A atividade principal é feita em duas etapas. Sugerimos fazer apenas a primeira parte. Para realização da atividade é necessário que os alunos já tenham conhecimento de algumas estratégias para transformar dízimas em fração geratriz.
Caso a turma não esteja familiarizada, você pode disponibilizar os slides que tratam da discussão da solução para que os alunos analisem. Pode propor a produção de um texto para explicitar o que eles compreenderam da solução apresentada.
É provável que esta aula precise ser retomada. O raio X e as atividades complementares podem ser utilizadas para aulas futuras.
Sugestões de apreciação de vídeos da Khan Academy:
Link 1 - disponível aqui.
Link 2 - disponível aqui.
Discussão das soluções
Talvez haja necessidade de disponibilizar, para ampliação das compreensões dos alunos, os slides das discussões das soluções. Você pode utilizar aplicativos Whatsapp para os alunos encaminharem os textos.
É possível que essa aula necessite de outros momentos de retomada. Se houver recursos tecnológicos para discussão em tempo real com a turma, utilize-os para esclarecer dúvidas e sugerir propostas que ampliem as compreensões. Sugestão de recursos on line para discussões: Meet ou Hangout (Google).
Sistematização
xxx
Encerramento
xxx
Raio X
O Raio X pode ser proposto como revisão das aprendizagens, bem como as atividades complementares.
Convite às famílias
xxx
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Juliana Malta de Sousa
Mentor: Amanda Ferreira Verardo Bilia
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF08MA05 - Reconhecer e utilizar procedimentos para a obtenção de uma fração geratriz para uma dízima periódica.
Objetivos específicos
Obter a fração geratriz de dízimas periódicas compostas.
Conhecimentos prévios
Resolver equação de primeiro grau e simplificar frações.
Conceito-chave
Fração geratriz, dizima periódica simples e composta.
Recursos necessários
- Folha de papel A4 branca
- calculadora
- atividades impressas