Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientações: Projete ou leia o objetivo para a turma. O objetivo dessa aula é fazer com que os alunos consigam resolver divisões envolvendo números inteiros utilizando cálculo mental.
Propósito: Compartilhar o objetivo da aula.
Materiais complementares:
Operações com números inteiros (página 1)
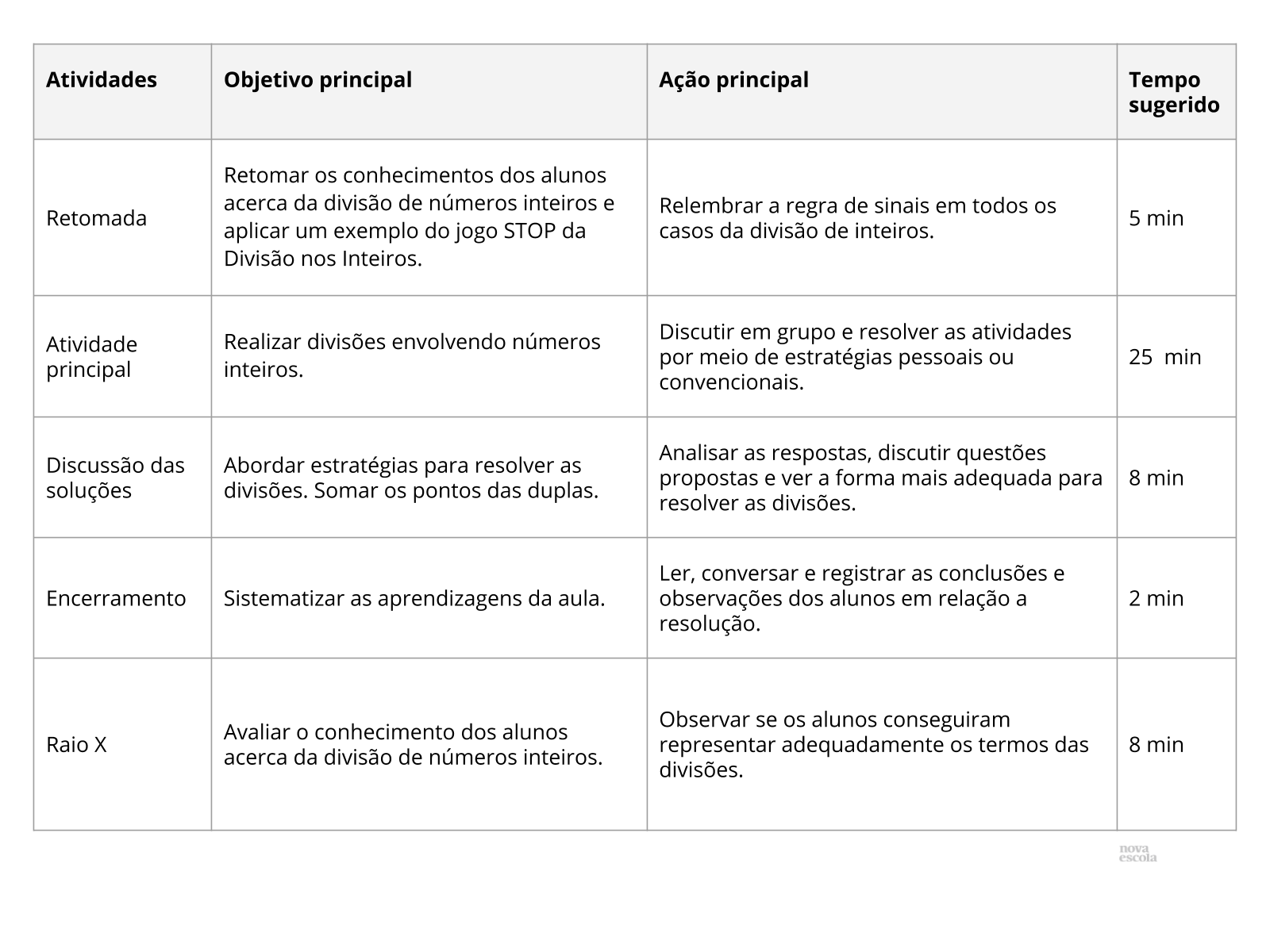
Retomada

Tempo sugerido: 5 minutos (Slides 3 e 4)
Orientação: A proposta da retomada é que, além de retomar as regras de sinais da divisão de números inteiros, você possa apresentar alguns exemplos envolvendo divisão de números inteiros, em que o resultado também é um número inteiro. Proponha uma divisão em que o resultado não seja um número inteiro, como por exemplo, 28 : 3 e pergunte aos alunos qual seria o quociente. Destaque que, nesse caso, a divisão teria um quociente decimal ou, trabalhando com inteiros, teríamos um resto na divisão. Evite falas como: “Menos com menos dá mais”, “Mais com menos dá menos”, etc. Isso causa grande confusão com os alunos ao trabalharem com soma e subtração, após terem trabalhado multiplicação e divisão.
Propósito: Relembrar a divisão de números inteiros.
Discuta com a turma:
- A regra de sinais na divisão de inteiros é importante?
- Quando os sinais são iguais, qual será o sinal do quociente?
- Quando os sinais são diferentes, qual será o sinal do quociente?
Respostas:
-30 ÷ (-5) = 6
30 ÷ 5 = 6
30 ÷ (-5) = -6
-30 ÷ 5 = -6
Retomada
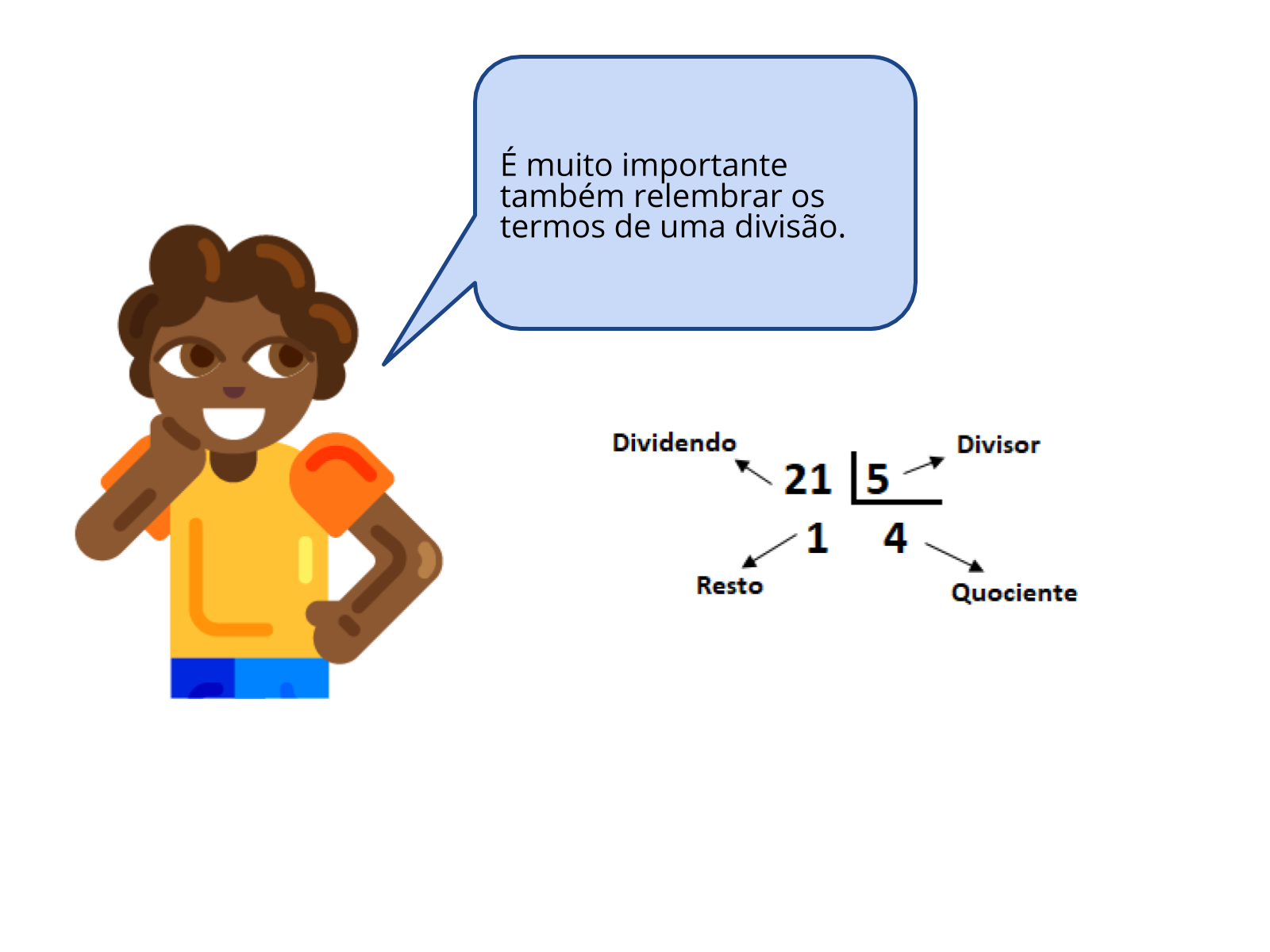
Tempo sugerido: 5 minutos (Slides 3 e 4)
Orientação: Destaque também quais são os termos de uma divisão. Apresente a divisão com o algoritmo e a divisão escrita em forma de expressão: 21 = 4 x 5 +1. Converse também sobre o resto e porque ele poderá ocorrer nas divisões com números inteiros.
Propósito: Relembrar a divisão de números inteiros.
Discuta com a turma:
- Em que situações teremos resto na divisão?
- Se quisermos trabalhar com quociente decimal, qual o próximo passo?
Atividade Principal

Tempo sugerido: 25 minutos (Slides 5 a 8)
Orientação: Dê um exemplo de como o jogo funciona. Retome as regras de sinais da divisão de números inteiros, para que você possa apresentar um exemplo de como funciona o jogo STOP da Divisão nos Inteiros. Evite falas como: “Menos com menos dá mais”, “Mais com menos dá menos”, etc. Isso causa grande confusão com os alunos ao trabalharem com soma e subtração, após terem trabalhado multiplicação e divisão.
Propósito: Relembrar a divisão de números inteiros.
Discuta com a turma:
- A regra de sinais na divisão de inteiros é importante?
- O cálculo mental nos ajuda nesse jogo?
- Vocês entenderam como funciona o jogo?
Material complementar:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Leitura sugerida - Aprendizado do trabalho em grupo: aqui.
Como jogar Stop: aqui.
Atividade Principal

Tempo sugerido: 25 minutos (Slides 5 a 8)
Orientação: Leia as regras com os alunos, destacando uma por uma e dê um exemplo de cada se for necessário. Certifique-se que todos entenderam a regra 1 para depois ler a 2 e assim por diante. Retome o exemplo utilizado anteriormente, se necessário. Você poderá utilizar os números que quiser no jogo, porém números que apresentem uma quantidade razoável de divisores tornarão o jogo mais interessante.
Números sugeridos para o jogo: 10; -20; 24; 8; 60; -32; -8; -25.
Propósito: Deixar as regras do jogo claras para os alunos.
Material complementar:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Leitura sugerida - Aprendizado do trabalho em grupo: aqui.
Como jogar Stop: aqui.
Atividade Principal

Tempo sugerido: 25 minutos (Slides 5 a 8)
Orientação: Leia as regras com os alunos, destacando uma por uma e dê um exemplo de cada se for necessário. Certifique-se que todos entenderam a regra 1 para depois ler a 2 e assim por diante. Retome o exemplo utilizado anteriormente, se necessário. Você poderá utilizar os números que quiser no jogo, porém números que apresentem uma quantidade razoável de divisores tornarão o jogo mais interessante.
Números sugeridos para o jogo: 10; -20; 24; 8; 60; -32; -8; -25.
Propósito: Deixar as regras do jogo claras para os alunos.
Material complementar:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Leitura sugerida - Aprendizado do trabalho em grupo: aqui.
Como jogar Stop: aqui.
Atividade Principal
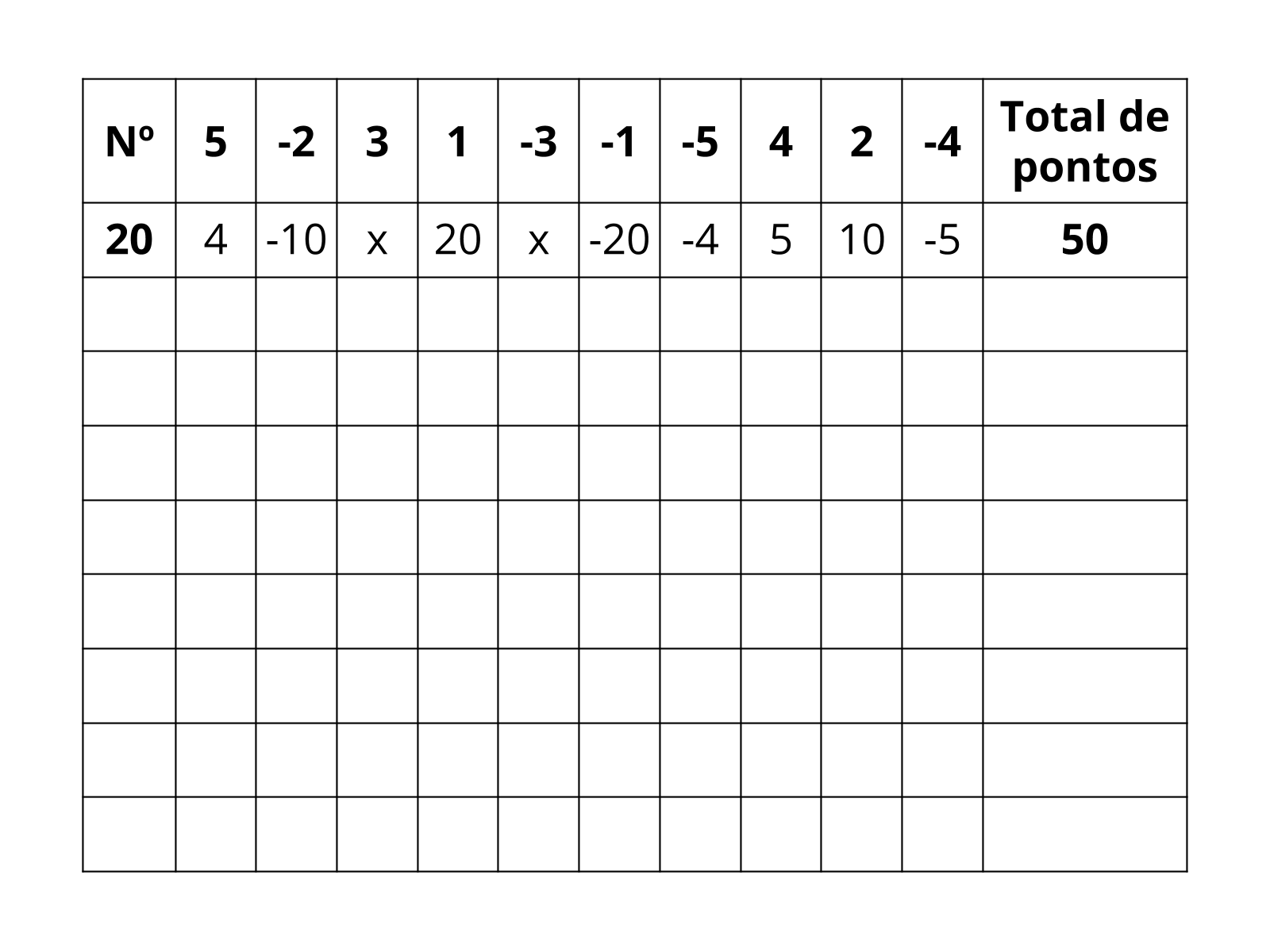
Tempo sugerido: 25 minutos (Slides 5 a 8)
Orientação: Números sugeridos para o jogo: 10; -20; 24; 8; 60; -32; -8; -25.
É importante ver os resultados e pontuação a cada número ditado. Observe se há dúvidas ou erros nas primeiras linhas. Depois os alunos ficarão mais acostumados. Você pode conversar com a classe sobre a honestidade na hora da correção, pois é importante que eles corrijam com cuidado, sem alterações e com cuidado na hora da soma. Você também pode pedir que anotem as respostas com caneta e que rasuras não são permitidas.
Propósito: Orientar os alunos e conduzir a atividade.
Material complementar:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Leitura sugerida - Aprendizado do trabalho em grupo: aqui.
Como jogar Stop: aqui.
Discussão das soluções
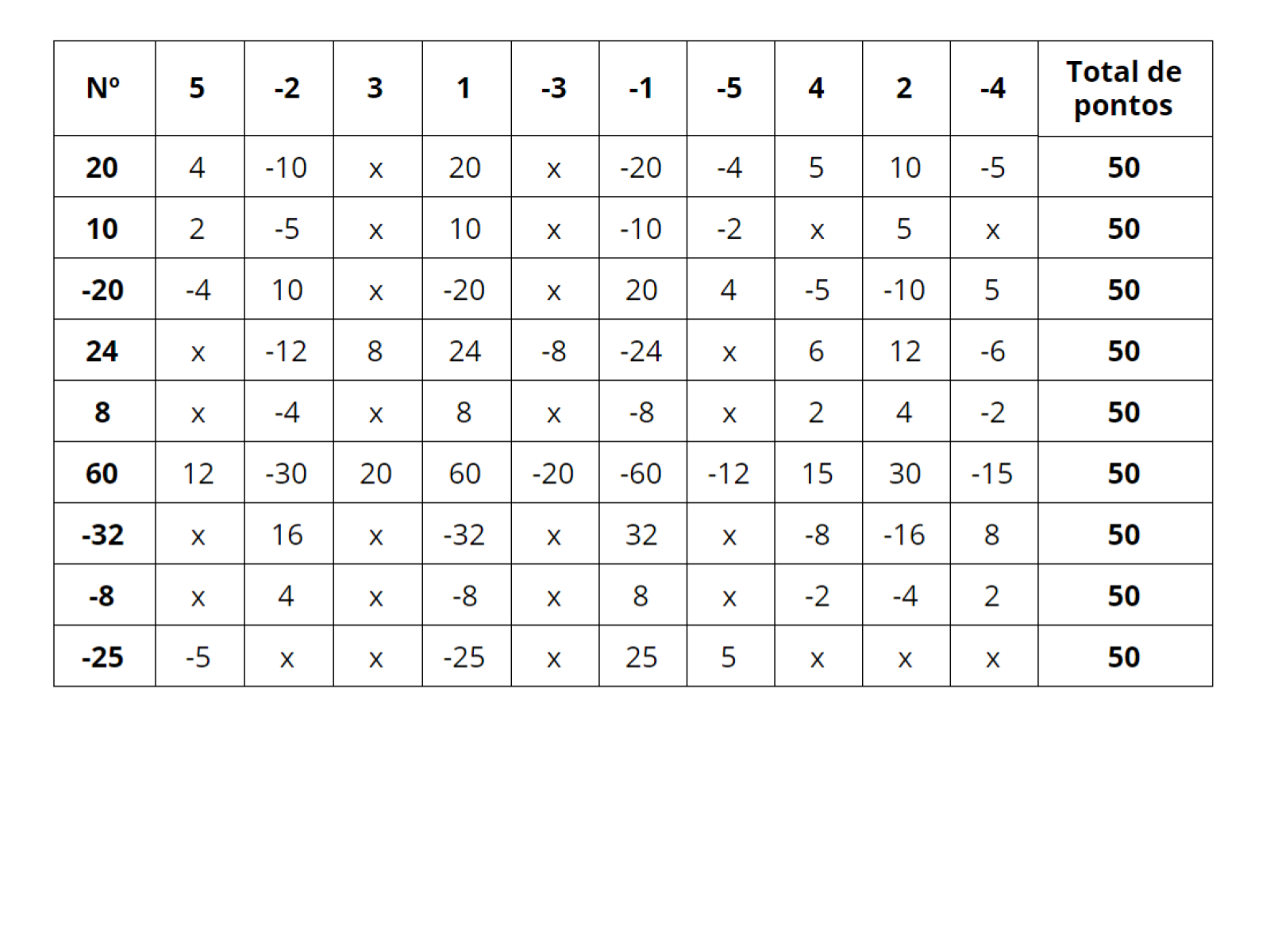
Tempo sugerido: 8 minutos
Orientação:
- Os números que aparecem na correção são os números que foram sugeridos anteriormente. Deixe projetada a tabela, organize-a no quadro ou num cartaz.
- A cada rodada você colocará os resultados na lousa para que os alunos possam acompanhar a correção, conforme for sendo falado pela dupla que falou STOP!.
- A maioria das divisões podem ser realizadas tranquilamente de forma mental, porém os alunos podem realizar os algoritmos. O objetivo aqui é verificar se os alunos estão compreendendo a regra de sinais e utilizando-a de maneira adequada e organizada.
- Proponha para que alguma dupla dê dicas de como pensaram para resolver o jogo ou se elaboraram alguma estratégia específica. Por exemplo: um resolvia os números positivos e o outro aluno os negativos; um resolvia as divisões e o outro anotava; um resolvia e o outro corrigia;
- A proposta é para que eles possam demonstrar estratégias pessoais para resolver uma divisão envolvendo números inteiros.
Discuta com a turma:
- Se você fosse dar uma dica sobre o jogo, qual seria?
- É mais fácil realizar os cálculos mentalmente ou com o algoritmo?
- Existe algum padrão encontrado na tabela?
Propósito: Observar se os alunos compreenderam a divisão envolvendo números inteiros e se os sinais do quociente estão adequados.
Material complementar:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Leitura sugerida - Aprendizado do trabalho em grupo: aqui.
Como jogar Stop: aqui.
Encerramento

Tempo sugerido: 2 minutos
Orientação: Comente sobre a atividade realizada, discuta sobre as estratégias de resolução de cada dupla e ouça os alunos sobre as suas impressões em relação ao jogo.
Propósito: Finalizar a aula com comentários dos alunos sobre o que compreenderam da atividade.
Raio X

Tempo sugerido: 8 minutos
Orientação: Essa atividade deve ser realizada individualmente. Os alunos deverão se recordar dos termos de uma divisão (conteúdo amplamente explorado em anos anteriores) e como fazer para encontrá-los. Eles podem utilizar a operação inversa ou por tentativa e erro. Em uma linguagem mais simplificada para os alunos, os termos são:
Dividendo: “número que será dividido”.
Divisor: “por quanto será dividido”.
Quociente: “resultado”.
Resto: “o valor que sobra”.
Propósito: Realizar divisões envolvendo números inteiros, utilizando a operação inversa quando necessário.
Materiais complementares:
Raio X
Resolução do raio x
Atividade complementar
Resolução da atividade complementar

























