Atividade Principal
Plano de Aula
Plano de aula: Aplicando frações como operador em diferentes contextos
Plano 4 de uma sequência de 5 planos. Veja todos os planos sobre As frações em nosso dia a dia
Por: Luiz Filipe Trovão
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Luiz Filipe Trovão
Mentor: Ferdinando Caíque Genghini Dantas Lobo
Especialista: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF07MA06 - Reconhecer que as resoluções de um grupo de problemas que têm a mesma estrutura podem ser obtidas utilizando os mesmo procedimentos.
EF07MA08 - Comparar e ordenar frações associadas às ideias de partes de inteiros, resultado da divisão, razão e operador.
EF07MA09 - Utilizar, na resolução de problemas, a associação entre razão e fração, como a fração 2/3 para expressar a razão de duas partes de uma grandeza para três partes da mesma ou três partes de outra grandeza.
Objetivos específicos
- Efetuar multiplicações envolvendo uma fração e um número natural;
- Realizar uma análise de várias situações problema envolvendo o uso de frações como operador.
Conceito-chave
Multiplicação de uma fração por um número natural; Fração como operador.
Recursos necessários
Lápis, borracha e caderno.
Habilidades BNCC:
Objetivos de aprendizagem
- Efetuar multiplicações envolvendo uma fração e um número natural;
- Realizar uma análise de várias situações problema envolvendo o uso de frações como operador.
Resumo da aula
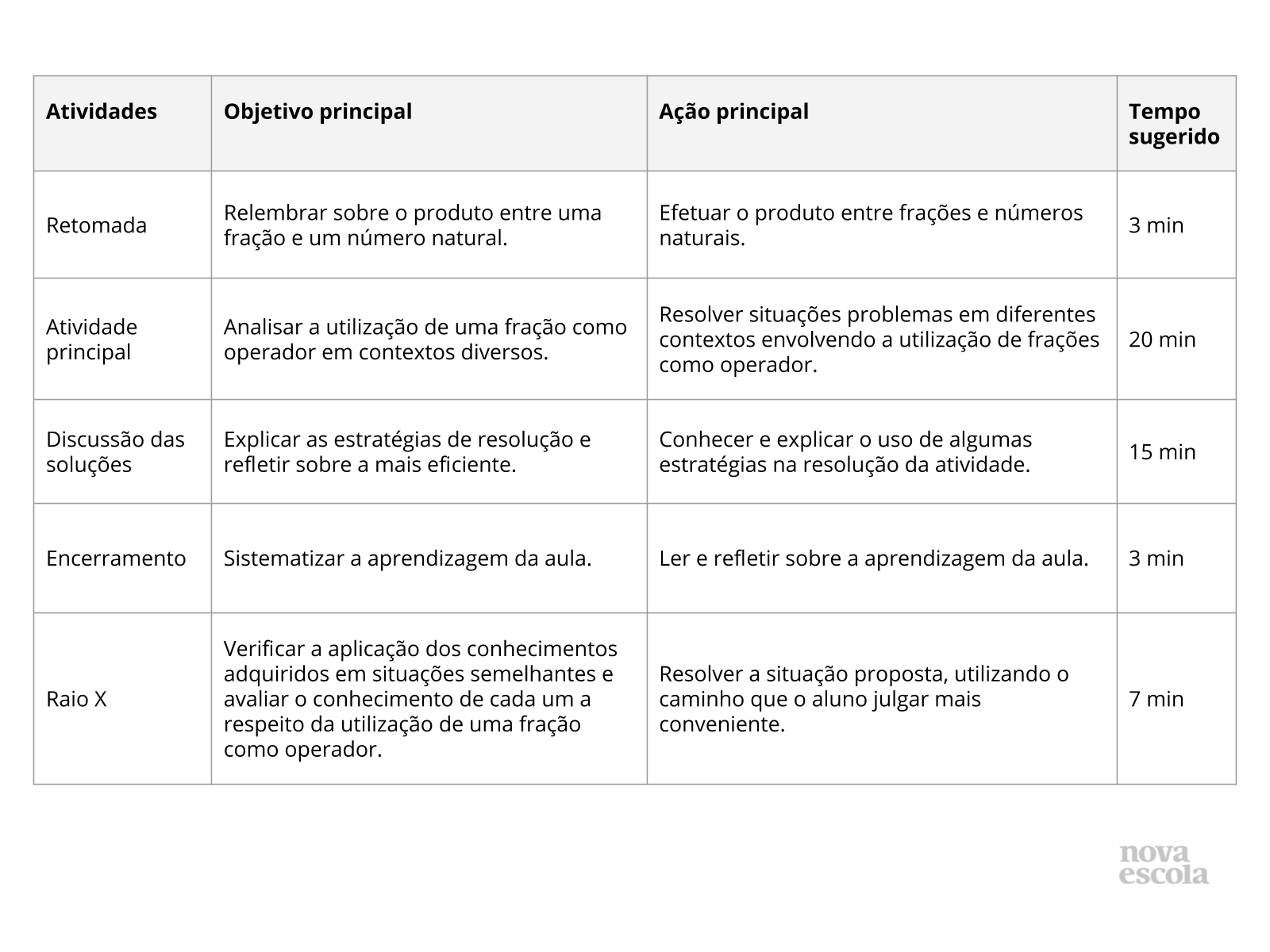
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Materiais complementares:
Acesse o arquivo sobre o plano aqui.
Leituras:
- Nova ordem numérica: https://novaescola.org.br/conteudo/2657/nova-ordem-numerica
- Introdução aos números racionais: https://novaescola.org.br/conteudo/2722/introducao-aos-numeros-racionais
- Dividir as dúvidas para compreender as frações: https://novaescola.org.br/conteudo/2135/dividir-as-duvidas-para-compreender-as-fracoes
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma. Caso não seja possível a projeção, escreva o objetivo no quadro.
Propósito: Compartilhar o objetivo da aula.
Aquecimento

Tempo sugerido: 3 minutos
Orientação: Professor, projete os slides para a sala. Caso não seja possível a projeção, leia a pergunta presente no balão de fala e escreva no quadro ou em um cartaz o restante do slide.
Realize a pergunta presente no balão de fala. Ela tem o intuito de iniciar a aula, apontando o que os alunos farão nesse primeiro momento, que é a realização de produtos entre números naturais e frações, diga para eles que a prática que será realizada nesse momento, será muito importante para o bom desenvolvimento do restante da aula.
Dê um tempo para que eles resolvam o que foi solicitado, acompanhe-os em seus raciocínios tirando as dúvidas que possam surgir durante a resolução.
- 15 x 2/3 = 30/3 = 10;
- 11 x 1/5 = 11/5 = 2,2.
Após o tempo dado aos alunos, apresente a resposta e relembre com eles que em alguns casos a divisão não será exata (como por exemplo o segundo produto). Caso a resposta final apresentada por eles seja uma fração, estimule-os a eles dar mais um passo e chegar na representação decimal.
Propósito: Realizar o produto entre números naturais e frações de forma conceitual.
Discuta com a turma:
- Há alguma outra forma de resolver o produto entre um número natural e uma fração, diferente do que foi apresentado? Qual?
- O quociente entre numerador e denominador de uma fração será sempre exato?
Atividade Principal

Tempo sugerido: 20 minutos (slides 4 a 6)
Orientação: Imprima a atividade principal, entregue para os alunos e peça para que eles realizem a leitura das três situações que compõem a atividade. Caso não seja possível a projeção, o professor deverá escrever as situações no quadro ou confeccionar um cartaz.
Explique para os alunos que essa atividade será composta inicialmente por três situações, que serão resolvidas e discutidas em trios ( para mais informações e possibilidades sobre formações de grupos, consulte as sugestões de leituras e vídeos presentes em Materiais Complementares, ao final dessas anotações).
Professor, discuta com os alunos sobre as possibilidades existentes nas situações, atentando-se as possíveis dúvidas que possam surgir e disponibilize um tempo de, pelo menos, 15 minutos para que os alunos a resolvam as 3 situações.
Todas as situações têm como intenção, trabalhar o emprego de frações como operador, em diferentes contextos. Por isso é muito importante que os alunos se atentem a operação envolvida na fração como operador que é a multiplicação, que foi retomada préviamente no início da aula.
Nas situações 1 e 2 os itens já indicam de maneira clara as frações que serão utilizadas, testando a atenção dos alunos em casos, onde a fração dada é referente a uma quantidade, porém a pergunta faz referência a outra quantidade, como por exemplo o item “c” da situação 2: “Se 5/8 do quintal for de lajotas marrons, qual será a área ocupada pelas lajotas brancas?”, nele é informado a fração referente a área de lajotas marrons, porém a pergunta é referente a área ocupada pelas lajotas brancas.
Já na situação 3, as frações não são apontadas de maneira explícita. Os alunos poderão, antes de calcular as respostas dos itens, descobrir a fração que corresponde a cada um deles.
Propósito: Resolver situações problema diversas, que envolvem o uso de frações como operador.
Discuta com a turma:
- O que as frações representam nas situações 1 e 2?
- É possível que o valor encontrado seja maior que o total, por exemplo na situação 1, é possível que em algum item o valor encontrado seja maior que 4 horas? Por quê?
- A situação 3 também pode envolver o uso de frações? Como?
Materiais complementares para impressão:
Resolução da Atividade Principal
Leituras:
Como agrupo meus alunos: https://novaescola.org.br/conteudo/1475/como-agrupo-meus-alunos
O aprendizado do trabalho em grupo: https://novaescola.org.br/conteudo/605/o-aprendizado-do-trabalho-em-grupo
Vídeo:
Estratégias para formação de grupos: https://novaescola.org.br/conteudo/4063/estrategias-para-formacao-de-grupos
Atividade Principal

Tempo sugerido: 20 minutos (slides 4 a 6)
Orientação: Imprima a atividade principal, entregue para os alunos e peça para que eles realizem a leitura das três situações que compõem a atividade. Caso não seja possível a projeção, o professor deverá escrever as situações no quadro ou confeccionar um cartaz.
Explique para os alunos que essa atividade será composta inicialmente por três situações, que serão resolvidas e discutidas em trios ( para mais informações e possibilidades sobre formações de grupos, consulte as sugestões de leituras e vídeos presentes em Materiais Complementares, ao final dessas anotações).
Professor, discuta com os alunos sobre as possibilidades existentes nas situações, atentando-se as possíveis dúvidas que possam surgir e disponibilize um tempo de, pelo menos, 15 minutos para que os alunos a resolvam as 3 situações.
Todas as situações têm como intenção, trabalhar o emprego de frações como operador, em diferentes contextos. Por isso é muito importante que os alunos se atentem a operação envolvida na fração como operador que é a multiplicação, que foi retomada préviamente no início da aula.
Nas situações 1 e 2 os itens já indicam de maneira clara as frações que serão utilizadas, testando a atenção dos alunos em casos, onde a fração dada é referente a uma quantidade, porém a pergunta faz referência a outra quantidade, como por exemplo o item “c” da situação 2: “Se 5/8 do quintal for de lajotas marrons, qual será a área ocupada pelas lajotas brancas?”, nele é informado a fração referente a área de lajotas marrons, porém a pergunta é referente a área ocupada pelas lajotas brancas.
Já na situação 3, as frações não são apontadas de maneira explícita. Os alunos poderão, antes de calcular as respostas dos itens, descobrir a fração que corresponde a cada um deles.
Propósito: Resolver situações problema diversas, que envolvem o uso de frações como operador.
Discuta com a turma:
- O que as frações representam nas situações 1 e 2?
- É possível que o valor encontrado seja maior que o total, por exemplo na situação 1, é possível que em algum item o valor encontrado seja maior que 4 horas? Por quê?
- A situação 3 também pode envolver o uso de frações? Como?
Materiais complementares para impressão:
Resolução da Atividade Principal
Leituras:
Como agrupo meus alunos: https://novaescola.org.br/conteudo/1475/como-agrupo-meus-alunos
O aprendizado do trabalho em grupo: https://novaescola.org.br/conteudo/605/o-aprendizado-do-trabalho-em-grupo
Vídeo:
Estratégias para formação de grupos: https://novaescola.org.br/conteudo/4063/estrategias-para-formacao-de-grupos
Atividade Principal
Tempo sugerido: 20 minutos (slides 4 a 6)
Orientação: Imprima a atividade principal, entregue para os alunos e peça para que eles realizem a leitura das três situações que compõem a atividade. Caso não seja possível a projeção, o professor deverá escrever as situações no quadro ou confeccionar um cartaz.
Explique para os alunos que essa atividade será composta inicialmente por três situações, que serão resolvidas e discutidas em trios ( para mais informações e possibilidades sobre formações de grupos, consulte as sugestões de leituras e vídeos presentes em Materiais Complementares, ao final dessas anotações).
Professor, discuta com os alunos sobre as possibilidades existentes nas situações, atentando-se as possíveis dúvidas que possam surgir e disponibilize um tempo de, pelo menos, 15 minutos para que os alunos a resolvam as 3 situações.
Todas as situações têm como intenção, trabalhar o emprego de frações como operador, em diferentes contextos. Por isso é muito importante que os alunos se atentem a operação envolvida na fração como operador que é a multiplicação, que foi retomada préviamente no início da aula.
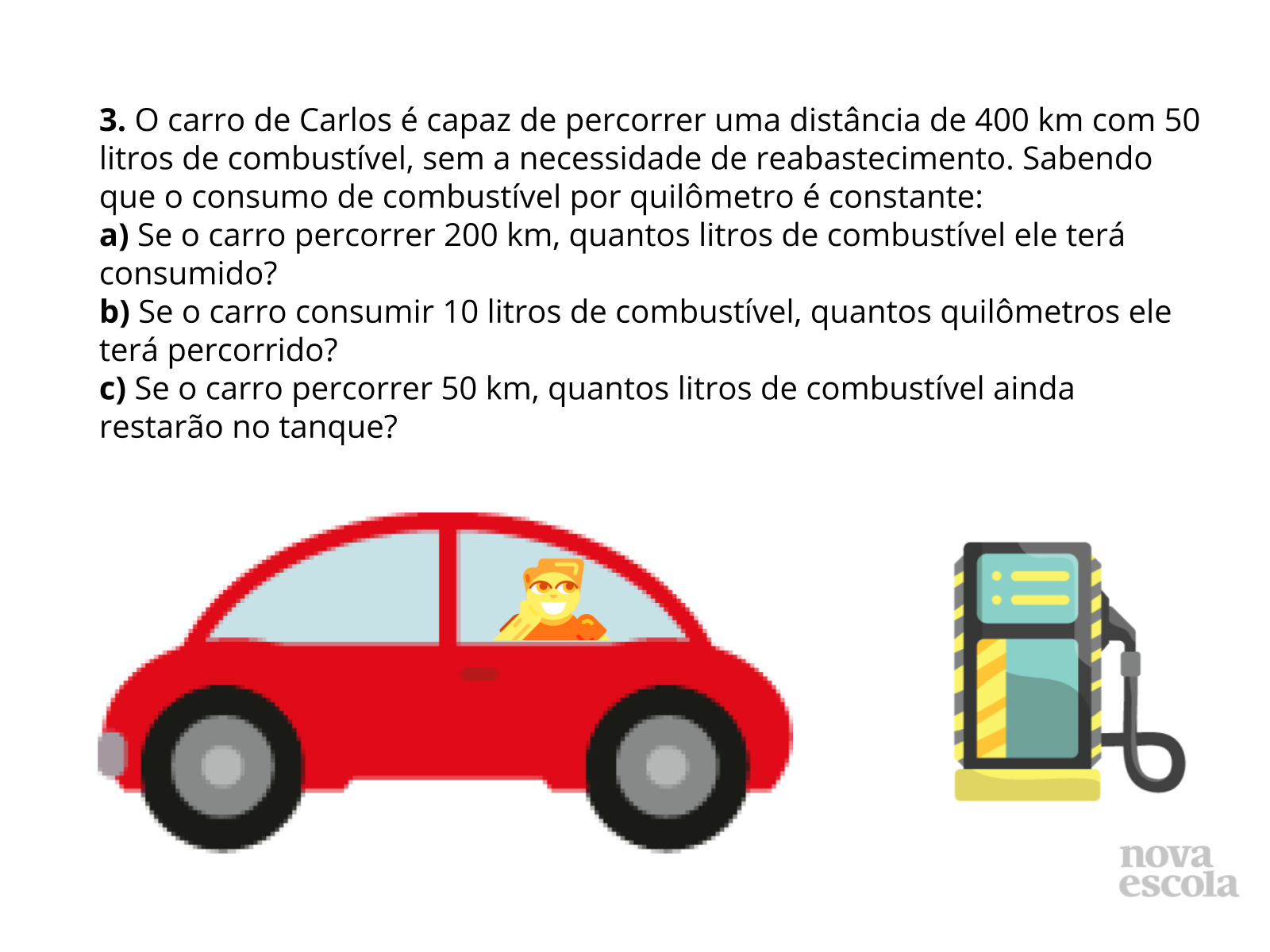
Nas situações 1 e 2 os itens já indicam de maneira clara as frações que serão utilizadas, testando a atenção dos alunos em casos, onde a fração dada é referente a uma quantidade, porém a pergunta faz referência a outra quantidade, como por exemplo o item “c” da situação 2: “Se 5/8 do quintal for de lajotas marrons, qual será a área ocupada pelas lajotas brancas?”, nele é informado a fração referente a área de lajotas marrons, porém a pergunta é referente a área ocupada pelas lajotas brancas.
Já na situação 3, as frações não são apontadas de maneira explícita. Os alunos poderão, antes de calcular as respostas dos itens, descobrir a fração que corresponde a cada um deles.
Propósito: Resolver situações problema diversas, que envolvem o uso de frações como operador.
Discuta com a turma:
- O que as frações representam nas situações 1 e 2?
- É possível que o valor encontrado seja maior que o total, por exemplo na situação 1, é possível que em algum item o valor encontrado seja maior que 4 horas? Por quê?
- A situação 3 também pode envolver o uso de frações? Como?
Materiais complementares para impressão:
Resolução da Atividade Principal
Leituras:
Como agrupo meus alunos: https://novaescola.org.br/conteudo/1475/como-agrupo-meus-alunos
O aprendizado do trabalho em grupo: https://novaescola.org.br/conteudo/605/o-aprendizado-do-trabalho-em-grupo
Vídeo:
Estratégias para formação de grupos: https://novaescola.org.br/conteudo/4063/estrategias-para-formacao-de-grupos
Discussão da solução
Tempo sugerido: 15 minutos (Slides 7 a 15)
Orientação: Inicialmente, peça para que os alunos, ainda em trios, discutam as soluções que obtiveram na resolução das três situações, sempre acompanhando os grupos em seus raciocínios, pedindo em seguida para que os grupos as exponham para a sala.
Para otimizar esse processo, sugira que cada grupo apresente a solução de um item de cada situação, o 1º grupo apresenta a solução do item “a” da situação 1, o 2º grupo, do item “b” e assim por diante. Quanto mais grupos apresentarem os seus raciocínios mais rica será a discussão.
Após os grupos compartilharem as estratégias utilizadas na resolução das situações, passe para essa série de slides. Caso não seja possível a projeção, o professor deverá reproduzir, pelo menos os cálculos realizados, no quadro ou em um cartaz, o restante da solução pode ser compartilhada para a sala.
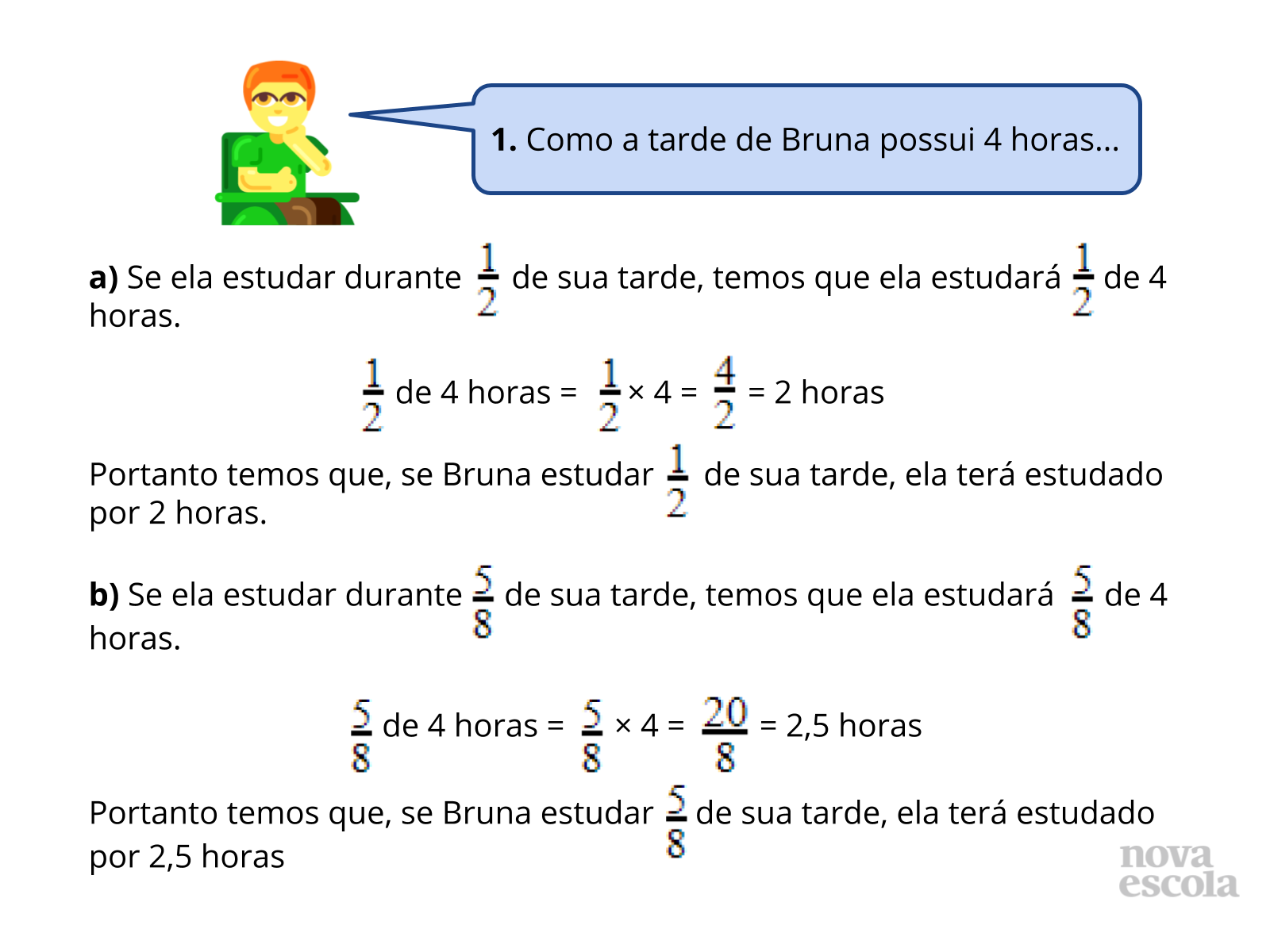
As resoluções das situações 1 (slides 7 e 8) e 2 (slides 9 a 11), apresentam a realização do produto entre uma fração e um número natural, pois, todas as frações utilizadas já foram fornecidas no enunciado dos itens, a resolução da situação 3 (slides 12 a 14) exige um pouco mais dos alunos, as frações não foram informadas, elas poderão ser encontradas de acordo com as informações presentes na situação, mais precisamente os valores 400 km e 50 litros, é a partir desses dois valores que todas as frações necessárias foram encontradas.
Professor, a atividade tem como intuito mostrar que a utilização da fração como operador está presente em diversos contextos e a sua realização é a mesma independente da situação descrita.
Por isso, após passar por todas as resoluções da atividade, realize a pergunta presente no slide 15 “O que essas situações têm em comum?”. Dê um tempo para os alunos pensarem sobre o questionamento e observe as respostas que eles fornecerem.
Espere como resposta dos alunos: o fato de que em todas elas as frações estavam presentes e foram utilizadas como operador; o produto entre a fração e um número natural foi essencial para a descoberta do valor solicitado; todas envolvem o conceito de fração de uma quantia.
Propósito: Apresentar e compartilhar meios utilizados na obtenção da solução, a fim de expor diferentes caminhos para se obter o mesmo resultado.
Discuta com a turma:
- O que essas situações têm em comum?
- Quais as operações matemáticas envolvidas na solução dessa atividade?
Materiais complementares para impressão:
Resolução da Atividade Principal
Discussão da solução

Tempo sugerido: 15 minutos (Slides 7 a 15)
Orientação: Inicialmente, peça para que os alunos, ainda em trios, discutam as soluções que obtiveram na resolução das três situações, sempre acompanhando os grupos em seus raciocínios, pedindo em seguida para que os grupos as exponham para a sala.
Para otimizar esse processo, sugira que cada grupo apresente a solução de um item de cada situação, o 1º grupo apresenta a solução do item “a” da situação 1, o 2º grupo, do item “b” e assim por diante. Quanto mais grupos apresentarem os seus raciocínios mais rica será a discussão.
Após os grupos compartilharem as estratégias utilizadas na resolução das situações, passe para essa série de slides. Caso não seja possível a projeção, o professor deverá reproduzir, pelo menos os cálculos realizados, no quadro ou em um cartaz, o restante da solução pode ser compartilhada para a sala.
As resoluções das situações 1 (slides 7 e 8) e 2 (slides 9 a 11), apresentam a realização do produto entre uma fração e um número natural, pois, todas as frações utilizadas já foram fornecidas no enunciado dos itens, a resolução da situação 3 (slides 12 a 14) exige um pouco mais dos alunos, as frações não foram informadas, elas poderão ser encontradas de acordo com as informações presentes na situação, mais precisamente os valores 400 km e 50 litros, é a partir desses dois valores que todas as frações necessárias foram encontradas.
Professor, a atividade tem como intuito mostrar que a utilização da fração como operador está presente em diversos contextos e a sua realização é a mesma independente da situação descrita.
Por isso, após passar por todas as resoluções da atividade, realize a pergunta presente no slide 15 “O que essas situações têm em comum?”. Dê um tempo para os alunos pensarem sobre o questionamento e observe as respostas que eles fornecerem.
Espere como resposta dos alunos: o fato de que em todas elas as frações estavam presentes e foram utilizadas como operador; o produto entre a fração e um número natural foi essencial para a descoberta do valor solicitado; todas envolvem o conceito de fração de uma quantia.
Propósito: Apresentar e compartilhar meios utilizados na obtenção da solução, a fim de expor diferentes caminhos para se obter o mesmo resultado.
Discuta com a turma:
- O que essas situações têm em comum?
- Quais as operações matemáticas envolvidas na solução dessa atividade?
Materiais complementares para impressão:
Resolução da Atividade Principal
Discussão da solução

Tempo sugerido: 15 minutos (Slides 7 a 15)
Orientação: Inicialmente, peça para que os alunos, ainda em trios, discutam as soluções que obtiveram na resolução das três situações, sempre acompanhando os grupos em seus raciocínios, pedindo em seguida para que os grupos as exponham para a sala.
Para otimizar esse processo, sugira que cada grupo apresente a solução de um item de cada situação, o 1º grupo apresenta a solução do item “a” da situação 1, o 2º grupo, do item “b” e assim por diante. Quanto mais grupos apresentarem os seus raciocínios mais rica será a discussão.
Após os grupos compartilharem as estratégias utilizadas na resolução das situações, passe para essa série de slides. Caso não seja possível a projeção, o professor deverá reproduzir, pelo menos os cálculos realizados, no quadro ou em um cartaz, o restante da solução pode ser compartilhada para a sala.
As resoluções das situações 1 (slides 7 e 8) e 2 (slides 9 a 11), apresentam a realização do produto entre uma fração e um número natural, pois, todas as frações utilizadas já foram fornecidas no enunciado dos itens, a resolução da situação 3 (slides 12 a 14) exige um pouco mais dos alunos, as frações não foram informadas, elas poderão ser encontradas de acordo com as informações presentes na situação, mais precisamente os valores 400 km e 50 litros, é a partir desses dois valores que todas as frações necessárias foram encontradas.
Professor, a atividade tem como intuito mostrar que a utilização da fração como operador está presente em diversos contextos e a sua realização é a mesma independente da situação descrita.
Por isso, após passar por todas as resoluções da atividade, realize a pergunta presente no slide 15 “O que essas situações têm em comum?”. Dê um tempo para os alunos pensarem sobre o questionamento e observe as respostas que eles fornecerem.
Espere como resposta dos alunos: o fato de que em todas elas as frações estavam presentes e foram utilizadas como operador; o produto entre a fração e um número natural foi essencial para a descoberta do valor solicitado; todas envolvem o conceito de fração de uma quantia.
Propósito: Apresentar e compartilhar meios utilizados na obtenção da solução, a fim de expor diferentes caminhos para se obter o mesmo resultado.
Discuta com a turma:
- O que essas situações têm em comum?
- Quais as operações matemáticas envolvidas na solução dessa atividade?
Materiais complementares para impressão:
Resolução da Atividade Principal
Discussão da solução

Tempo sugerido: 15 minutos (Slides 7 a 15)
Orientação: Inicialmente, peça para que os alunos, ainda em trios, discutam as soluções que obtiveram na resolução das três situações, sempre acompanhando os grupos em seus raciocínios, pedindo em seguida para que os grupos as exponham para a sala.
Para otimizar esse processo, sugira que cada grupo apresente a solução de um item de cada situação, o 1º grupo apresenta a solução do item “a” da situação 1, o 2º grupo, do item “b” e assim por diante. Quanto mais grupos apresentarem os seus raciocínios mais rica será a discussão.
Após os grupos compartilharem as estratégias utilizadas na resolução das situações, passe para essa série de slides. Caso não seja possível a projeção, o professor deverá reproduzir, pelo menos os cálculos realizados, no quadro ou em um cartaz, o restante da solução pode ser compartilhada para a sala.
As resoluções das situações 1 (slides 7 e 8) e 2 (slides 9 a 11), apresentam a realização do produto entre uma fração e um número natural, pois, todas as frações utilizadas já foram fornecidas no enunciado dos itens, a resolução da situação 3 (slides 12 a 14) exige um pouco mais dos alunos, as frações não foram informadas, elas poderão ser encontradas de acordo com as informações presentes na situação, mais precisamente os valores 400 km e 50 litros, é a partir desses dois valores que todas as frações necessárias foram encontradas.
Professor, a atividade tem como intuito mostrar que a utilização da fração como operador está presente em diversos contextos e a sua realização é a mesma independente da situação descrita.
Por isso, após passar por todas as resoluções da atividade, realize a pergunta presente no slide 15 “O que essas situações têm em comum?”. Dê um tempo para os alunos pensarem sobre o questionamento e observe as respostas que eles fornecerem.
Espere como resposta dos alunos: o fato de que em todas elas as frações estavam presentes e foram utilizadas como operador; o produto entre a fração e um número natural foi essencial para a descoberta do valor solicitado; todas envolvem o conceito de fração de uma quantia.
Propósito: Apresentar e compartilhar meios utilizados na obtenção da solução, a fim de expor diferentes caminhos para se obter o mesmo resultado.
Discuta com a turma:
- O que essas situações têm em comum?
- Quais as operações matemáticas envolvidas na solução dessa atividade?
Materiais complementares para impressão:
Resolução da Atividade Principal
Discussão da solução

Tempo sugerido: 15 minutos (Slides 7 a 15)
Orientação: Inicialmente, peça para que os alunos, ainda em trios, discutam as soluções que obtiveram na resolução das três situações, sempre acompanhando os grupos em seus raciocínios, pedindo em seguida para que os grupos as exponham para a sala.
Para otimizar esse processo, sugira que cada grupo apresente a solução de um item de cada situação, o 1º grupo apresenta a solução do item “a” da situação 1, o 2º grupo, do item “b” e assim por diante. Quanto mais grupos apresentarem os seus raciocínios mais rica será a discussão.
Após os grupos compartilharem as estratégias utilizadas na resolução das situações, passe para essa série de slides. Caso não seja possível a projeção, o professor deverá reproduzir, pelo menos os cálculos realizados, no quadro ou em um cartaz, o restante da solução pode ser compartilhada para a sala.
As resoluções das situações 1 (slides 7 e 8) e 2 (slides 9 a 11), apresentam a realização do produto entre uma fração e um número natural, pois, todas as frações utilizadas já foram fornecidas no enunciado dos itens, a resolução da situação 3 (slides 12 a 14) exige um pouco mais dos alunos, as frações não foram informadas, elas poderão ser encontradas de acordo com as informações presentes na situação, mais precisamente os valores 400 km e 50 litros, é a partir desses dois valores que todas as frações necessárias foram encontradas.
Professor, a atividade tem como intuito mostrar que a utilização da fração como operador está presente em diversos contextos e a sua realização é a mesma independente da situação descrita.
Por isso, após passar por todas as resoluções da atividade, realize a pergunta presente no slide 15 “O que essas situações têm em comum?”. Dê um tempo para os alunos pensarem sobre o questionamento e observe as respostas que eles fornecerem.
Espere como resposta dos alunos: o fato de que em todas elas as frações estavam presentes e foram utilizadas como operador; o produto entre a fração e um número natural foi essencial para a descoberta do valor solicitado; todas envolvem o conceito de fração de uma quantia.
Propósito: Apresentar e compartilhar meios utilizados na obtenção da solução, a fim de expor diferentes caminhos para se obter o mesmo resultado.
Discuta com a turma:
- O que essas situações têm em comum?
- Quais as operações matemáticas envolvidas na solução dessa atividade?
Materiais complementares para impressão:
Resolução da Atividade Principal
Discussão da solução
Tempo sugerido: 15 minutos (Slides 7 a 15)
Orientação: Inicialmente, peça para que os alunos, ainda em trios, discutam as soluções que obtiveram na resolução das três situações, sempre acompanhando os grupos em seus raciocínios, pedindo em seguida para que os grupos as exponham para a sala.
Para otimizar esse processo, sugira que cada grupo apresente a solução de um item de cada situação, o 1º grupo apresenta a solução do item “a” da situação 1, o 2º grupo, do item “b” e assim por diante. Quanto mais grupos apresentarem os seus raciocínios mais rica será a discussão.
Após os grupos compartilharem as estratégias utilizadas na resolução das situações, passe para essa série de slides. Caso não seja possível a projeção, o professor deverá reproduzir, pelo menos os cálculos realizados, no quadro ou em um cartaz, o restante da solução pode ser compartilhada para a sala.
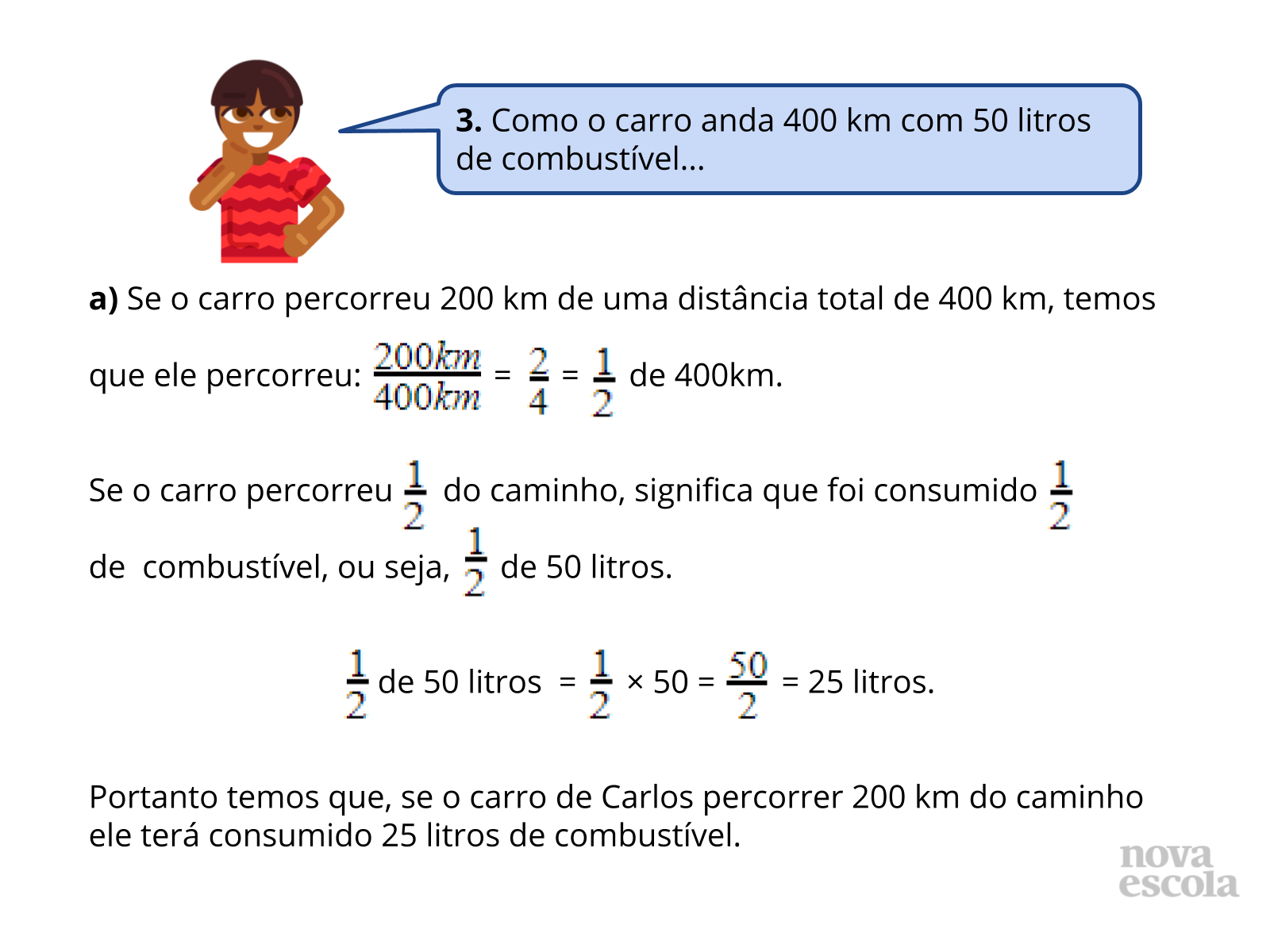
As resoluções das situações 1 (slides 7 e 8) e 2 (slides 9 a 11), apresentam a realização do produto entre uma fração e um número natural, pois, todas as frações utilizadas já foram fornecidas no enunciado dos itens, a resolução da situação 3 (slides 12 a 14) exige um pouco mais dos alunos, as frações não foram informadas, elas poderão ser encontradas de acordo com as informações presentes na situação, mais precisamente os valores 400 km e 50 litros, é a partir desses dois valores que todas as frações necessárias foram encontradas.
Professor, a atividade tem como intuito mostrar que a utilização da fração como operador está presente em diversos contextos e a sua realização é a mesma independente da situação descrita.
Por isso, após passar por todas as resoluções da atividade, realize a pergunta presente no slide 15 “O que essas situações têm em comum?”. Dê um tempo para os alunos pensarem sobre o questionamento e observe as respostas que eles fornecerem.
Espere como resposta dos alunos: o fato de que em todas elas as frações estavam presentes e foram utilizadas como operador; o produto entre a fração e um número natural foi essencial para a descoberta do valor solicitado; todas envolvem o conceito de fração de uma quantia.
Propósito: Apresentar e compartilhar meios utilizados na obtenção da solução, a fim de expor diferentes caminhos para se obter o mesmo resultado.
Discuta com a turma:
- O que essas situações têm em comum?
- Quais as operações matemáticas envolvidas na solução dessa atividade?
Materiais complementares para impressão:
Resolução da Atividade Principal
Discussão da solução

Tempo sugerido: 15 minutos (Slides 7 a 15)
Orientação: Inicialmente, peça para que os alunos, ainda em trios, discutam as soluções que obtiveram na resolução das três situações, sempre acompanhando os grupos em seus raciocínios, pedindo em seguida para que os grupos as exponham para a sala.
Para otimizar esse processo, sugira que cada grupo apresente a solução de um item de cada situação, o 1º grupo apresenta a solução do item “a” da situação 1, o 2º grupo, do item “b” e assim por diante. Quanto mais grupos apresentarem os seus raciocínios mais rica será a discussão.
Após os grupos compartilharem as estratégias utilizadas na resolução das situações, passe para essa série de slides. Caso não seja possível a projeção, o professor deverá reproduzir, pelo menos os cálculos realizados, no quadro ou em um cartaz, o restante da solução pode ser compartilhada para a sala.
As resoluções das situações 1 (slides 7 e 8) e 2 (slides 9 a 11), apresentam a realização do produto entre uma fração e um número natural, pois, todas as frações utilizadas já foram fornecidas no enunciado dos itens, a resolução da situação 3 (slides 12 a 14) exige um pouco mais dos alunos, as frações não foram informadas, elas poderão ser encontradas de acordo com as informações presentes na situação, mais precisamente os valores 400 km e 50 litros, é a partir desses dois valores que todas as frações necessárias foram encontradas.
Professor, a atividade tem como intuito mostrar que a utilização da fração como operador está presente em diversos contextos e a sua realização é a mesma independente da situação descrita.
Por isso, após passar por todas as resoluções da atividade, realize a pergunta presente no slide 15 “O que essas situações têm em comum?”. Dê um tempo para os alunos pensarem sobre o questionamento e observe as respostas que eles fornecerem.
Espere como resposta dos alunos: o fato de que em todas elas as frações estavam presentes e foram utilizadas como operador; o produto entre a fração e um número natural foi essencial para a descoberta do valor solicitado; todas envolvem o conceito de fração de uma quantia.
Propósito: Apresentar e compartilhar meios utilizados na obtenção da solução, a fim de expor diferentes caminhos para se obter o mesmo resultado.
Discuta com a turma:
- O que essas situações têm em comum?
- Quais as operações matemáticas envolvidas na solução dessa atividade?
Materiais complementares para impressão:
Resolução da Atividade Principal
Discussão da solução

Tempo sugerido: 15 minutos (Slides 7 a 15)
Orientação: Inicialmente, peça para que os alunos, ainda em trios, discutam as soluções que obtiveram na resolução das três situações, sempre acompanhando os grupos em seus raciocínios, pedindo em seguida para que os grupos as exponham para a sala.
Para otimizar esse processo, sugira que cada grupo apresente a solução de um item de cada situação, o 1º grupo apresenta a solução do item “a” da situação 1, o 2º grupo, do item “b” e assim por diante. Quanto mais grupos apresentarem os seus raciocínios mais rica será a discussão.
Após os grupos compartilharem as estratégias utilizadas na resolução das situações, passe para essa série de slides. Caso não seja possível a projeção, o professor deverá reproduzir, pelo menos os cálculos realizados, no quadro ou em um cartaz, o restante da solução pode ser compartilhada para a sala.
As resoluções das situações 1 (slides 7 e 8) e 2 (slides 9 a 11), apresentam a realização do produto entre uma fração e um número natural, pois, todas as frações utilizadas já foram fornecidas no enunciado dos itens, a resolução da situação 3 (slides 12 a 14) exige um pouco mais dos alunos, as frações não foram informadas, elas poderão ser encontradas de acordo com as informações presentes na situação, mais precisamente os valores 400 km e 50 litros, é a partir desses dois valores que todas as frações necessárias foram encontradas.
Professor, a atividade tem como intuito mostrar que a utilização da fração como operador está presente em diversos contextos e a sua realização é a mesma independente da situação descrita.
Por isso, após passar por todas as resoluções da atividade, realize a pergunta presente no slide 15 “O que essas situações têm em comum?”. Dê um tempo para os alunos pensarem sobre o questionamento e observe as respostas que eles fornecerem.
Espere como resposta dos alunos: o fato de que em todas elas as frações estavam presentes e foram utilizadas como operador; o produto entre a fração e um número natural foi essencial para a descoberta do valor solicitado; todas envolvem o conceito de fração de uma quantia.
Propósito: Apresentar e compartilhar meios utilizados na obtenção da solução, a fim de expor diferentes caminhos para se obter o mesmo resultado.
Discuta com a turma:
- O que essas situações têm em comum?
- Quais as operações matemáticas envolvidas na solução dessa atividade?
Materiais complementares para impressão:
Resolução da Atividade Principal
Discussão da solução

Tempo sugerido: 15 minutos (Slides 7 a 15)
Orientação: Inicialmente, peça para que os alunos, ainda em trios, discutam as soluções que obtiveram na resolução das três situações, sempre acompanhando os grupos em seus raciocínios, pedindo em seguida para que os grupos as exponham para a sala.
Para otimizar esse processo, sugira que cada grupo apresente a solução de um item de cada situação, o 1º grupo apresenta a solução do item “a” da situação 1, o 2º grupo, do item “b” e assim por diante. Quanto mais grupos apresentarem os seus raciocínios mais rica será a discussão.
Após os grupos compartilharem as estratégias utilizadas na resolução das situações, passe para essa série de slides. Caso não seja possível a projeção, o professor deverá reproduzir, pelo menos os cálculos realizados, no quadro ou em um cartaz, o restante da solução pode ser compartilhada para a sala.
As resoluções das situações 1 (slides 7 e 8) e 2 (slides 9 a 11), apresentam a realização do produto entre uma fração e um número natural, pois, todas as frações utilizadas já foram fornecidas no enunciado dos itens, a resolução da situação 3 (slides 12 a 14) exige um pouco mais dos alunos, as frações não foram informadas, elas poderão ser encontradas de acordo com as informações presentes na situação, mais precisamente os valores 400 km e 50 litros, é a partir desses dois valores que todas as frações necessárias foram encontradas.
Professor, a atividade tem como intuito mostrar que a utilização da fração como operador está presente em diversos contextos e a sua realização é a mesma independente da situação descrita.
Por isso, após passar por todas as resoluções da atividade, realize a pergunta presente no slide 15 “O que essas situações têm em comum?”. Dê um tempo para os alunos pensarem sobre o questionamento e observe as respostas que eles fornecerem.
Espere como resposta dos alunos: o fato de que em todas elas as frações estavam presentes e foram utilizadas como operador; o produto entre a fração e um número natural foi essencial para a descoberta do valor solicitado; todas envolvem o conceito de fração de uma quantia.
Propósito: Apresentar e compartilhar meios utilizados na obtenção da solução, a fim de expor diferentes caminhos para se obter o mesmo resultado.
Discuta com a turma:
- O que essas situações têm em comum?
- Quais as operações matemáticas envolvidas na solução dessa atividade?
Materiais complementares para impressão:
Encerramento

Tempo sugerido: 3 minutos
Orientação: Projete o slide e leia para os alunos a conclusão da aula. Caso não seja possível a projeção, copie a pergunta: “Quanto é 1/2 de 1/3 da área de um terreno qualquer?” no quadro, ou em um cartaz, bem como a resposta da mesma.
Nesse momento de encerramento da aula, são retomadas algumas situações onde as frações são utilizadas como operador e uma conclusão é feita a respeito dessa utilização quando o operador é realizado entre duas frações, mostrando que essa utilização também pode ser relacionada a uma situação cotidiana.
Propósito: Realizar a conclusão sobre a aula, retomando situações que utilizam frações como operador.
Raio X

Tempo sugerido: 7 minutos.
Orientação: Apresente a nova situação e peça para que os alunos analisem e resolvam, em um primeiro momento individualmente e em seguida compartilhando a forma de pensar com o colega ao lado. Você pode projetar, passar no quadro ou fazer o download desta atividade e entregar para os seus alunos. O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure anotar e identificar todos os comentários que surgirem.
Propósito: Realizar uma atividade teórica relativa aos conteúdos ensinados na aula.
Discuta com a turma:
- É possível afirmar qual amigo leu a maior quantidade de páginas olhando apenas para as frações correspondentes?
Materiais complementares para impressão:
Para os Alunos
Para o Professor
Sugestão de adaptação para ensino remoto
Código do plano
MAT7_06NUM04
Recursos
- Necessários:
- caderno
- lápis
- régua
- grupo de alunos no WhatsApp
- Opcionais:
- Google Sala de Aula
- Meet
- Formulário do Google
- vídeo: “Multiplicação de frações e números naturais”, disponível no Khan Academy https://youtu.be/Oei0dcQRHUY, acesso em 17 de jun 2020.
Para este plano, foque na etapa: Atividade Principal
Aquecimento
Professor use o Google Formulário para que os alunos respondam à atividade inicial digitando a resposta. Caso os alunos não tenham recursos digitais, o professor pode solicitar a resolução do problema proposto com as questões que estão indicadas nas orientações. Ou ainda você pode sugerir que os alunos, em um movimento de sala de aula invertida, assistam ao vídeo “Multiplicação de frações e números naturais”, disponível no Khan Academy para uma retomada.
Atividade principal
Professor, para a realização das atividades principal os alunos precisam ter acesso ao problema proposto. Para isso, fotografe e disponibilize a imagem no grupo de WhatsApp ou no Google Sala de Aula para que os alunos possam pensar sobre ele. Peça que tentem resolver a atividade em dois momentos. No primeiro momento, eles deverão pensar sozinhos sobre a situação proposta e anotar todas as suas estratégias de cálculo no caderno. No segundo momento, você pode sugerir que o aluno compartilhe a resposta com um familiar e juntos discutam as estratégias de resolução. Oriente-os a fotografar as suas estratégias e respostas para compartilhar com o professor e a turma no momento da discussão das soluções.
Discussão das soluções
Professor, caso esteja em uma aula síncrona, realize a discussão das soluções por meio de um debate de ideias, procurando apresentar mais de uma possibilidade de soluções. Nesse momento questione aos alunos: "O que essas situações têm em comum e quais as operações matemáticas envolvidas na solução dessa atividade?". Após fazer essas intervenções e ouvir dos alunos, seja por WhatsApp, Google Sala de Aula ou pelo Meet, por exemplo, sistematize a aula com os alunos.
Sistematização
Professor, as atividades têm como intuito mostrar que a utilização da fração como operador está presente em diversos contextos e a sua realização é a mesma independente da situação descrita. Se necessário, apresente mais algumas discussões para a turma.
Raio X
Proponha a resolução da atividade, enviando-a via WhatsApp, Google Sala de aula ou por meio de um formulário. Peça que compartilhe com o professor a resolução. Analise as resoluções e elabore devolutivas individuais para os alunos.
Convite às famílias
A participação das famílias no processo de aprendizagem é de grande importância para o aluno. Porém, ressaltamos que os pais não são professores de matemática e muitos estão ocupados com outras funções em casa. Portanto, indicamos a participação das famílias no compartilhamento e discussão de possíveis soluções para os problemas propostos.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Luiz Filipe Trovão
Mentor: Ferdinando Caíque Genghini Dantas Lobo
Especialista: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF07MA06 - Reconhecer que as resoluções de um grupo de problemas que têm a mesma estrutura podem ser obtidas utilizando os mesmo procedimentos.
EF07MA08 - Comparar e ordenar frações associadas às ideias de partes de inteiros, resultado da divisão, razão e operador.
EF07MA09 - Utilizar, na resolução de problemas, a associação entre razão e fração, como a fração 2/3 para expressar a razão de duas partes de uma grandeza para três partes da mesma ou três partes de outra grandeza.
Objetivos específicos
- Efetuar multiplicações envolvendo uma fração e um número natural;
- Realizar uma análise de várias situações problema envolvendo o uso de frações como operador.
Conceito-chave
Multiplicação de uma fração por um número natural; Fração como operador.
Recursos necessários
Lápis, borracha e caderno.









