Guia de Intervenção
Plano de Aula
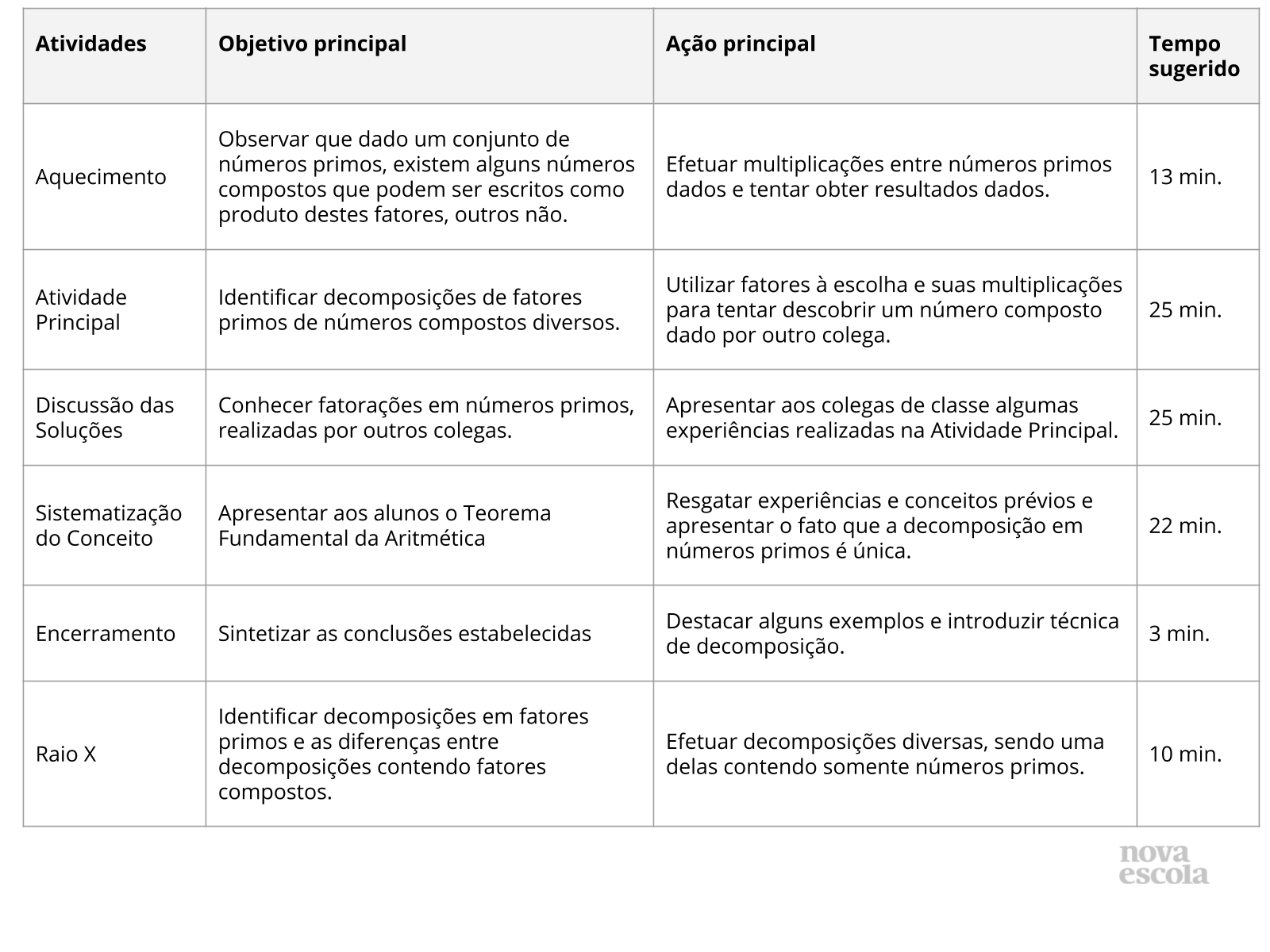
Plano de aula: Identificando decomposições em fatores primos
Plano 7 de uma sequência de 10 planos. Veja todos os planos sobre Números primos e compostos
Por: Allan Costa Jardim
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Allan Costa Jardim
Mentor: Rodrigo Morozetti Blanco
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
(EF06MA04) Classificar números naturais em primos e compostos, estabelecer relações entre números, expressas pelos termos “é múltiplo de”, “é divisor de”, “é fator de”, e estabelecer, por meio de investigações, critérios de divisibilidade por 2, 3, 4, 5, 6, 8, 9, 10, 100 e 1000;
(EF06MA05) Resolver e elaborar problemas que envolvam as ideias de múltiplo e de divisor;
Objetivos específicos
Identificar que números inteiros podem ser decompostos em fatores primos, identificar que a fatoração em fatores primos é única.
Conceito-chave
Múltiplos, fatores, divisibilidade, números primos, números compostos.
Recursos necessários
- Folha de papel A4 branca;
- Atividades impressas em folhas, coladas no caderno ou não.
- Arquivos anexos impressos (tabuleiro numérico (neste link) e retângulos para confecção de fichas (neste link));
- Grãos diversos (feijão, milho, arroz, etc…).
Habilidades BNCC:
Objetivos de aprendizagem
Identificar que números inteiros podem ser decompostos em fatores primos, identificar que a fatoração em fatores primos é única.