Atividade principal
Plano de Aula
Plano de aula: Analisando múltiplos em nosso dia a dia
Plano 4 de uma sequência de 7 planos. Veja todos os planos sobre Ampliação dos conceitos de múltiplos e divisores
Por: Luiz Filipe Trovão
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Luiz Filipe Trovão
Mentor: Ferdinando Caíque Genghini Dantas Lobo
Especialista: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF07MA01 - Resolver e elaborar problemas com números naturais, envolvendo as ideias de múltiplos, divisores e divisibilidade.
Objetivos específicos
- Resolver problemas envolvendo o conceito de múltiplos de um número natural.
Conceito-chave
Relação entre múltiplos e divisores.
Recursos necessários
Lápis, borracha e caderno;
Habilidades BNCC:
Objetivos de aprendizagem
- Resolver problemas envolvendo o conceito de múltiplos de um número natural.
Resumo da aula
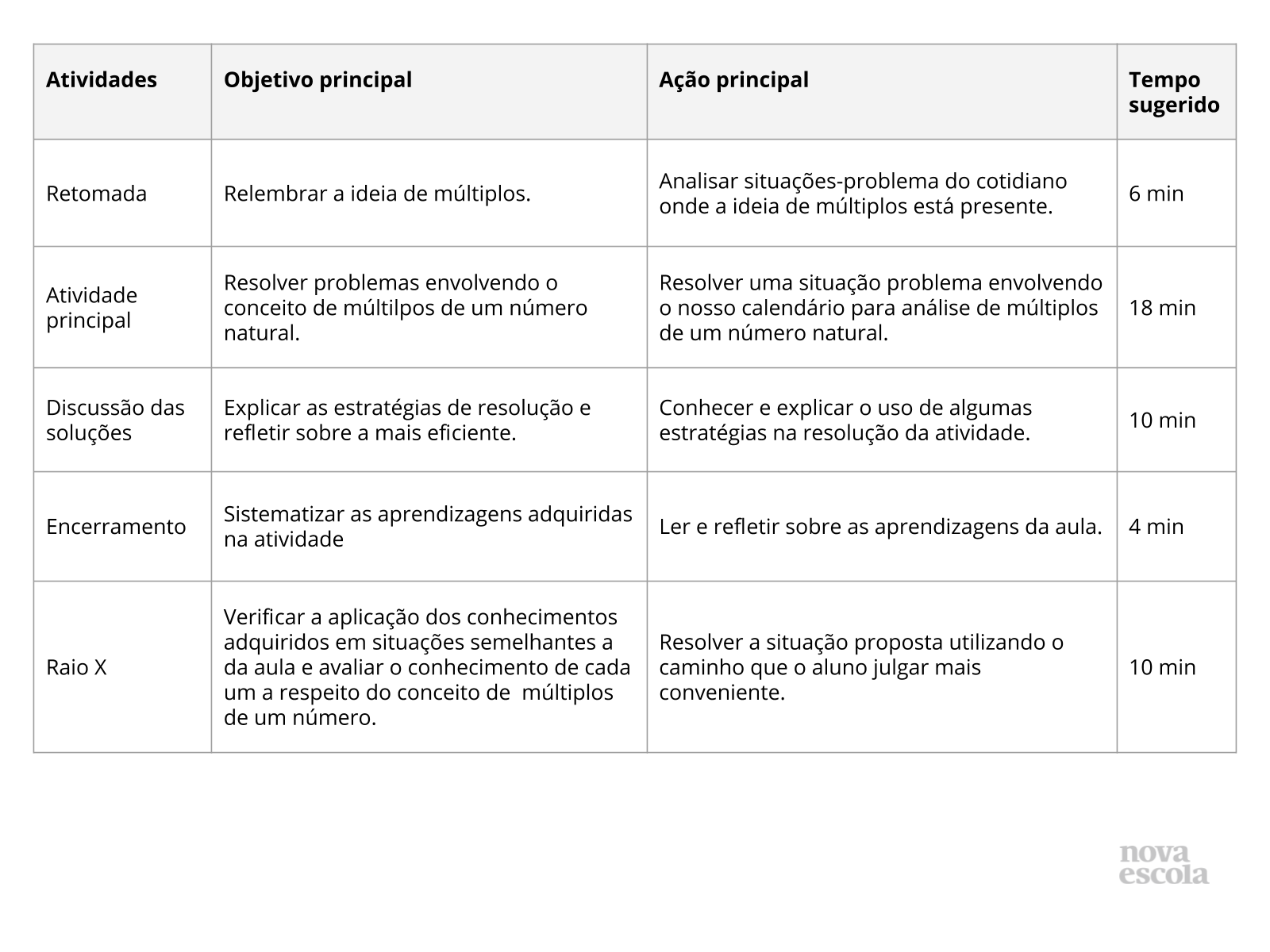
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Leituras complementares:
Tabuada sem medo: 5 jogos para ficar craque em multiplicação: https://novaescola.org.br/conteudo/9468/tabuada-sem-medo-5-jogos-para-ficar-craque
Divisibilidade: como ensiná-la à garotada: https://novaescola.org.br/conteudo/2136/divisibilidade-como-ensina-la-a-garotada
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete, escreva no quadro ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada

Tempo sugerido: 5 minutos (slides 3 e 4).
Orientações: Professor, projete essa série de slides para a sala. Caso não seja possível a projeção, copie no quadro ou em um cartaz as informações presentes no balão de fala do slide 3 e os requisitos para que um ano seja bissexto, presentes no slide 4. O restante poderá ser lido com a sala.
Inicialmente, realize a leitura das informações presentes no slide 3, que falam da motivação em relação à criação do ano bissexto. Explique para os alunos, todos os valores presentes nesse balão de fala, para que não haja dúvidas no momento em que essas informações forem utilizadas. É muito importante que os alunos entendam essa parte da aula como uma introdução ao que será visto em seguida.
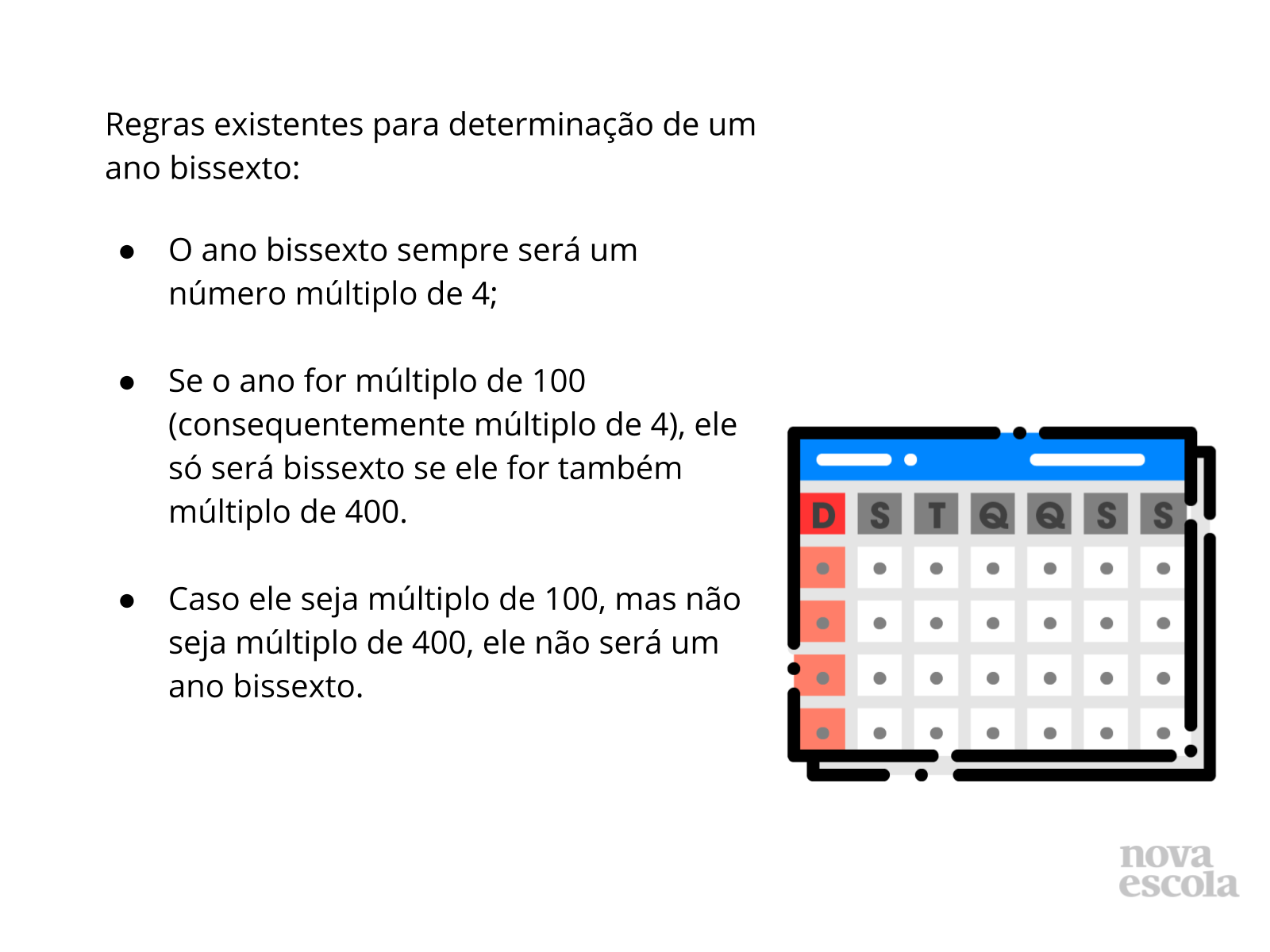
Após essa reflexão, passe para o slide 4 e aponte para os alunos as informações presentes nele, que são sobre os critérios existentes para que um ano seja bissexto. Todos os critérios são baseados na multiplicidade do número em questão:
- Todo ano bissexto é múltiplo do número 4;
- Se o ano for múltiplo de 100, ele só será bissexto se também for múltiplo de 400.
Finalize esse momento apontando que eles irão realizar uma atividade envolvendo a análise de anos bissextos.
Propósito: Analisar a presença de padrões envolvendo múltiplos em situações cotidianas
Discuta com a turma:
- Você já havia ouvido falar sobre anos bissextos?
- O que diferencia um ano bissexto dos outros “anos normais”?
Retomada
Tempo sugerido: 5 minutos (slides 3 e 4).
Orientações: Professor, projete essa série de slides para a sala. Caso não seja possível a projeção, copie no quadro ou em um cartaz as informações presentes no balão de fala do slide 3 e os requisitos para que um ano seja bissexto, presentes no slide 4. O restante poderá ser lido com a sala.
Inicialmente, realize a leitura das informações presentes no slide 3, que falam da motivação em relação à criação do ano bissexto. Explique para os alunos todos os valores presentes nesse balão de fala, para que não haja dúvidas no momento em que essas informações forem utilizadas. É muito importante que os alunos entendam essa parte da aula como uma introdução ao que será visto em seguida.
Após essa reflexão, passe para o slide 4 e aponte para os alunos as informações presentes nele, que são sobre os critérios existentes para que um ano seja bissexto. Todos os critérios são baseados na multiplicidade do número em questão:
- Todo ano bissexto é múltiplo do número 4;
- Se o ano for múltiplo de 100, ele só será bissexto se também for múltiplo de 400.
Finalize esse momento apontando que eles irão realizar uma atividade envolvendo a análise de anos bissextos.
Propósito: Analisar a presença de padrões envolvendo múltiplos em situações cotidianas
Discuta com a turma:
- Você já havia ouvido falar sobre anos bissextos?
- O que diferencia um ano bissexto dos outros “anos normais”?
Atividade principal

Tempo sugerido: 18 minutos
Orientação: Imprima a atividade principal, entregue para os alunos e leia juntamente com eles as situações apresentadas na atividade. Caso não seja possível a projeção, escreva a situação no quadro ou confeccione um cartaz.
Explique para os alunos que a atividade será composta por três situações (I, II e III), onde algumas datas serão analisadas a fim de verificação da coincidência ou não com anos bissextos.
A primeira situação (I) mostra uma pergunta direta em relação a duas datas específicas, como forma de verificação rápida se os anos em questão são bissextos ou não.
As outras duas situações fazem referências a eventos reais: Copa do Mundo de Futebol (II) e Jogos Olímpicos (III). Algumas problemáticas são lançadas a fim de verificar se esses eventos ocorreram ou ocorrerão em algum momento de sua existência em datas coincidentes com anos bissextos. Será interessante a análise dos alunos a respeito dos anos em que ocorreram Jogos Olímpicos e foram bissextos e o porquê de 1900 não ser um ano bissexto, mas 2000 ser.
Propósito: Analisar datas presentes no cotidiano para verificar a existência de anos bissextos nas mesmas.
Discuta com a turma:
- Se em determinado ano, a Copa do Mundo de Futebol não ocorrer em um ano bissexto, existe a possibilidade de que em algum outro ano desse evento, essa situação se altere?
- É possível afirmar que ao ocorrer em um ano bissexto, todos os Jogos Olímpicos irão ocorrer em anos assim? Por quê?
Materiais complementares:
Discussão da solução

Tempo sugerido: 10 minutos (slides 6 a 9)
Orientação: Inicialmente, peça para que os alunos discutam as soluções das situações propostas em duplas, sempre acompanhando-os em seus raciocínios. Em seguida, peça para que alguns alunos exponham suas resoluções. A ideia não é direcionar para que determinado aluno apresente a solução, porém quanto mais caminhos diferentes forem apresentados para se chegar na mesma resposta, mais rica será a discussão.
Após os alunos compartilharem as estratégias utilizadas na resolução da atividade, passe para essa série de slides (6 a 9). Caso não seja possível a projeção, reproduza, pelo menos os cálculos realizados para se chegar aos valores solicitados no quadro ou em um cartaz, o restante da solução poderá ser lida com a sala.
A ideia principal na solução dessas situações é a utilização dos critérios existentes na determinação de um ano bissexto, utilizando a ideia de multiplicidade. Em todas as situações são analisados alguns anos, para essa verificação.
A “situação I”, tem como intuito apenas a verificação do uso da divisão por 4. A solução demonstra os dois valores da atividade sendo divididos por 4, para verificar que os dos valores é múltiplo de 4 (portanto bissexto) e o outro não (portanto não bissexto).
Na “situação II” é feita referência ao evento Copa do Mundo de Futebol. A ideia é verificar se em algum momento esse evento ocorreu ou irá ocorrer em um ano bissexto. É realizada uma verificação com os primeiros anos de ocorrência do evento. Note que, além de verificar que nenhuma das datas foi um ano bissexto, o valor obtido na divisão por 4, segue um mesmo padrão, um número decimal, onde o 5 é o algarismo dos décimos. Reflita com os alunos para o fato de que, como o período de ocorrência da Copa é o mesmo que o da ocorrência de um ano bissexto, ou seja, 4 anos, esses eventos nunca irão se coincidir, enquanto a Copa do Mundo possuir essa configuração.
Na “situação III” é analisado outro evento real, os Jogos Olímpicos. A ideia principal da resolução continua sendo a verificação se esse evento ocorrerá em ano bissexto, tendo como base a situação anterior (da Copa do Mundo de Futebol), não é necessário testar várias datas para verificar se os eventos são coincidentes. Como os Jogos Olímpicos ocorrem a cada 4 anos, e o ano bissexto também, basta verificar a existência de uma coincidência para generalizar as outras. Os únicos pontos de atenção que essa situação exige é em relação aos anos de 1900 e 2000, ambos são múltiplos de 4 e de 100 e, para que eles sejam bissextos, há a necessidade de que eles também sejam múltiplos e 400. Após os cálculos verifica-se que o ano de 2000 atende aos três requisitos, portanto é um ano bissexto algo que não ocorreu com o ano de 1900.
Propósito: Apresentar e compartilhar meios utilizados na obtenção da solução, a fim de expor diferentes caminhos para se obter o mesmo resultado.
Discuta com a turma:
- Todo ano múltiplo de 4 é um ano bissexto?
- Todo múltiplo de 4 é multiplo de 100? E de 400?
- Todo múltiplo de 400 é multiplo de 100? E o inverso?
- Há outra forma de se determinar se um ano é bissexto?
Discussão da solução

Tempo sugerido: 10 minutos (slides 6 a 9)
Orientação: Inicialmente, peça para que os alunos discutam as soluções das situações propostas em duplas, sempre acompanhando-os em seus raciocínios. Em seguida, peça para que alguns alunos exponham suas resoluções. A ideia não é direcionar para que determinado aluno apresente a solução, porém quanto mais caminhos diferentes forem apresentados para se chegar na mesma resposta, mais rica será a discussão.
Após os alunos compartilharem as estratégias utilizadas na resolução da atividade, passe para essa série de slides (6 a 9). Caso não seja possível a projeção, reproduza, pelo menos os cálculos realizados para se chegar aos valores solicitados no quadro ou em um cartaz, o restante da solução poderá ser lida com a sala.
A ideia principal na solução dessas situações é a utilização dos critérios existentes na determinação de um ano bissexto, utilizando a ideia de multiplicidade. Em todas as situações são analisados alguns anos, para essa verificação.
A “situação I”, tem como intuito apenas a verificação do uso da divisão por 4. A solução demonstra os dois valores da atividade sendo divididos por 4, para verificar que os dos valores é múltiplo de 4 (portanto bissexto) e o outro não (portanto não bissexto).
Na “situação II” é feita referência ao evento Copa do Mundo de Futebol. A ideia é verificar se em algum momento esse evento ocorreu ou irá ocorrer em um ano bissexto. É realizada uma verificação com os primeiros anos de ocorrência do evento. Note que, além de verificar que nenhuma das datas foi um ano bissexto, o valor obtido na divisão por 4, segue um mesmo padrão, um número decimal, onde o 5 é o algarismo dos décimos. Reflita com os alunos para o fato de que, como o período de ocorrência da Copa é o mesmo que o da ocorrência de um ano bissexto, ou seja, 4 anos, esses eventos nunca irão se coincidir, enquanto a Copa do Mundo possuir essa configuração.
Na “situação III” é analisado outro evento real, os Jogos Olímpicos. A ideia principal da resolução continua sendo a verificação se esse evento ocorrerá em ano bissexto, tendo como base a situação anterior (da Copa do Mundo de Futebol), não é necessário testar várias datas para verificar se os eventos são coincidentes. Como os Jogos Olímpicos ocorrem a cada 4 anos, e o ano bissexto também, basta verificar a existência de uma coincidência para generalizar as outras. Os únicos pontos de atenção que essa situação exige é em relação aos anos de 1900 e 2000, ambos são múltiplos de 4 e de 100 e, para que eles sejam bissextos, há a necessidade de que eles também sejam múltiplos e 400. Após os cálculos verifica-se que o ano de 2000 atende aos três requisitos, portanto é um ano bissexto algo que não ocorreu com o ano de 1900.
Propósito: Apresentar e compartilhar meios utilizados na obtenção da solução, a fim de expor diferentes caminhos para se obter o mesmo resultado.
Discuta com a turma:
- Todo ano múltiplo de 4 é um ano bissexto?
- Todo múltiplo de 4 é multiplo de 100? E de 400?
- Todo múltiplo de 400 é multiplo de 100? E o inverso?
- Há outra forma de se determinar se um ano é bissexto?
Discussão da solução

Tempo sugerido: 10 minutos (slides 6 a 9)
Orientação: Inicialmente, peça para que os alunos discutam as soluções das situações propostas em duplas, sempre acompanhando-os em seus raciocínios. Em seguida, peça para que alguns alunos exponham suas resoluções. A ideia não é direcionar para que determinado aluno apresente a solução, porém quanto mais caminhos diferentes forem apresentados para se chegar na mesma resposta, mais rica será a discussão.
Após os alunos compartilharem as estratégias utilizadas na resolução da atividade, passe para essa série de slides (6 a 9). Caso não seja possível a projeção, reproduza, pelo menos os cálculos realizados para se chegar aos valores solicitados no quadro ou em um cartaz, o restante da solução poderá ser lida com a sala.
A ideia principal na solução dessas situações é a utilização dos critérios existentes na determinação de um ano bissexto, utilizando a ideia de multiplicidade. Em todas as situações são analisados alguns anos, para essa verificação.
A “situação I”, tem como intuito apenas a verificação do uso da divisão por 4. A solução demonstra os dois valores da atividade sendo divididos por 4, para verificar qual dos valores é múltiplo de 4 (portanto bissexto) e o outro não (portanto não bissexto).
Na “situação II” é feita referência ao evento Copa do Mundo de Futebol. A ideia é verificar se em algum momento esse evento ocorreu ou irá ocorrer em um ano bissexto. É realizada uma verificação com os primeiros anos de ocorrência do evento. Note que, além de verificar que nenhuma das datas foi um ano bissexto, o valor obtido na divisão por 4, segue um mesmo padrão, um número decimal, onde o 5 é o algarismo dos décimos. Reflita com os alunos o fato de que, como o período de ocorrência da Copa é o mesmo que o da ocorrência de um ano bissexto, ou seja, 4 anos, esses eventos nunca irão se coincidir, enquanto a Copa do Mundo possuir essa configuração.
Na “situação III” é analisado outro evento real, os Jogos Olímpicos. A ideia principal da resolução continua sendo a verificação se esse evento ocorrerá em ano bissexto, tendo como base a situação anterior (da Copa do Mundo de Futebol), não é necessário testar várias datas para verificar se os eventos são coincidentes. Como os Jogos Olímpicos ocorrem a cada 4 anos, e o ano bissexto também, basta verificar a existência de uma coincidência para generalizar as outras. Os únicos pontos de atenção que essa situação exige são em relação aos anos de 1900 e 2000, ambos são múltiplos de 4 e de 100 e, para que eles sejam bissextos, há a necessidade de que eles também sejam múltiplos e 400. Após os cálculos verifica-se que o ano de 2000 atende aos três requisitos, portanto é um ano bissexto algo que não ocorreu com o ano de 1900.
Propósito: Apresentar e compartilhar meios utilizados na obtenção da solução, a fim de expor diferentes caminhos para se obter o mesmo resultado.
Discuta com a turma:
- Todo ano múltiplo de 4 é um ano bissexto?
- Todo múltiplo de 4 é multiplo de 100? E de 400?
- Todo múltiplo de 400 é multiplo de 100? E o inverso?
- Há outra forma de se determinar se um ano é bissexto?
Discussão da solução

Tempo sugerido: 10 minutos (slides 6 a 9)
Orientação: Inicialmente, peça para que os alunos discutam as soluções das situações propostas em duplas, sempre acompanhando-os em seus raciocínios. Em seguida, peça para que alguns alunos exponham suas resoluções. A ideia não é direcionar para que determinado aluno apresente a solução, porém quanto mais caminhos diferentes forem apresentados para se chegar na mesma resposta, mais rica será a discussão.
Após os alunos compartilharem as estratégias utilizadas na resolução da atividade, passe para essa série de slides (6 a 9). Caso não seja possível a projeção, reproduza, pelo menos os cálculos realizados para se chegar aos valores solicitados no quadro ou em um cartaz, o restante da solução poderá ser lida com a sala.
A ideia principal na solução dessas situações é a utilização dos critérios existentes na determinação de um ano bissexto, utilizando a ideia de multiplicidade. Em todas as situações são analisados alguns anos, para essa verificação.
A “situação I”, tem como intuito apenas a verificação do uso da divisão por 4. A solução demonstra os dois valores da atividade sendo divididos por 4, para verificar que os dos valores é múltiplo de 4 (portanto bissexto) e o outro não (portanto não bissexto).
Na “situação II” é feita referência ao evento Copa do Mundo de Futebol. A ideia é verificar se em algum momento esse evento ocorreu ou irá ocorrer em um ano bissexto. É realizada uma verificação com os primeiros anos de ocorrência do evento. Note que, além de verificar que nenhuma das datas foi um ano bissexto, o valor obtido na divisão por 4, segue um mesmo padrão, um número decimal, onde o 5 é o algarismo dos décimos. Reflita com os alunos para o fato de que, como o período de ocorrência da Copa é o mesmo que o da ocorrência de um ano bissexto, ou seja, 4 anos, esses eventos nunca irão se coincidir, enquanto a Copa do Mundo possuir essa configuração.
Na “situação III” é analisado outro evento real, os Jogos Olímpicos. A ideia principal da resolução continua sendo a verificação se esse evento ocorrerá em ano bissexto, tendo como base a situação anterior (da Copa do Mundo de Futebol), não é necessário testar várias datas para verificar se os eventos são coincidentes. Como os Jogos Olímpicos ocorrem a cada 4 anos, e o ano bissexto também, basta verificar a existência de uma coincidência para generalizar as outras. Os únicos pontos de atenção que essa situação exige é em relação aos anos de 1900 e 2000, ambos são múltiplos de 4 e de 100 e, para que eles sejam bissextos, há a necessidade de que eles também sejam múltiplos e 400. Após os cálculos verifica-se que o ano de 2000 atende aos três requisitos, portanto é um ano bissexto algo que não ocorreu com o ano de 1900.
Propósito: Apresentar e compartilhar meios utilizados na obtenção da solução, a fim de expor diferentes caminhos para se obter o mesmo resultado.
Discuta com a turma:
- Todo ano múltiplo de 4 é um ano bissexto?
- Todo múltiplo de 4 é multiplo de 100? E de 400?
- Todo múltiplo de 400 é multiplo de 100? E o inverso?
- Há outra forma de se determinar se um ano é bissexto?
Encerramento

Tempo sugerido: 4 minutos.
Orientação: Projete o slide e leia para os alunos a conclusão da aula. Caso não seja possível a projeção, copie no quadro ou em um cartaz, pelo menos os apontamentos sobre múltiplos e divisores no meio do slide.
Nesse momento de encerramento da aula, é realizada uma reflexão sobre a relação existentes entre múltiplos e divisores, conclui-se sobre o fato de que a análise de múltiplos e divisores podem ser realizadas em uma mesma situação, diferenciando-se apenas do ponto de vista da análise.
Para que os alunos compreendam um pouco melhor, aponte para eles que por 1888 ser múltiplo do número 4, podemos concluir que o número 4 divide 1888. (Se necessário, dê outro exemplo para que eles compreendam um pouco melhor). Como 1900 é múltiplo do número 100, podemos concluir que o número 100 divide 1900.
Finalize o encerramento apontando que o 0 (zero) é o único número múltiplo de todos os outros, ao mesmo tempo que não é divisor de nenhum número.
Propósito: Realizar a conclusão da aula, refletindo sobre as relações existente entre múltiplos e divisores.
Raio x

Tempo sugerido: 10 minutos
Orientação: Apresente a nova situação e peça para que os alunos analisem e resolvam, em um primeiro momento individualmente e em seguida compartilhando a forma de pensar com o colega ao lado. Você pode projetar, passar no quadro ou fazer o download desta atividade e entregar para os seus alunos. O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure anotar e identificar todos os comentários que surgirem.
Propósito: Realizar uma atividade teórica relativa aos conteúdos ensinados na aula.
Materiais complementares:
Para os alunos
Para o professor
Sugestão de adaptação para ensino remoto
Recursos
Necessários:
- Caderno;
- Lápis;
- Régua;
- Grupo de alunos no Whatsapp.
Opcionais:
- Google Sala de Aula.
Para este plano, foque na etapa Atividade Principal.
Aquecimento
A atividade é uma retomada de conceitos fundamentais para a aula. Os alunos precisarão saber o que é ano bissexto e como ele é determinado. Você pode propor que assistam ao vídeo “Ano bissexto: Conheça o conceito e a importancia” (disponível aqui). Atente-se ao fato de que se trata de um vídeo curto, para que não tenha um alto consumo no pacote de dados dos alunos e famílias.
Atividade principal
Para a realização da atividade principal os alunos precisam ter acesso ao problema proposto. Para isso, tire uma foto e disponibilize a imagem no grupo de Whatsapp, para que eles possam pensar. Oriente-os a filmarem ou fotografarem as estratégias e respostas para compartilharem com você e a turma no momento da discussão das soluções.
Discussão das soluções
A discussão das soluções da atividade é uma etapa importantíssima da aula. É o momento de justificar as estratégias e respostas usadas para a resolução do problema proposto na atividade principal. Os alunos devem postar os vídeos ou fotografias para compartilhar as respostas em um ambiente de interação, como Whatsapp ou Google Sala de Aula.
A intenção é formar um painel de soluções e promover uma discussão rica e estimuladora entre alunos e professor. Neste momento, estimule a turma a falar (usando a ferramenta de áudio ou vídeo) como pensou para resolver o problema. Lance as perguntas disponíveis no plano para mediar as discussões. Estimule a turma a perceber que, para conhecer uma solução, podemos seguir por diversos caminhos e o erro é uma importante ferramenta para o ensino-aprendizagem, que combate a valorização excessiva da resposta certa.
Convite às famílias
A participação das famílias no processo de aprendizagem é de grande importância para os alunos. Porém, ressaltamos que os pais não são professores de matemática e muitos estão ocupados com outras funções em casa.
Portanto indicamos a participação das famílias no compartilhamento e discussão de possíveis soluções para os problemas propostos.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Luiz Filipe Trovão
Mentor: Ferdinando Caíque Genghini Dantas Lobo
Especialista: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF07MA01 - Resolver e elaborar problemas com números naturais, envolvendo as ideias de múltiplos, divisores e divisibilidade.
Objetivos específicos
- Resolver problemas envolvendo o conceito de múltiplos de um número natural.
Conceito-chave
Relação entre múltiplos e divisores.
Recursos necessários
Lápis, borracha e caderno;