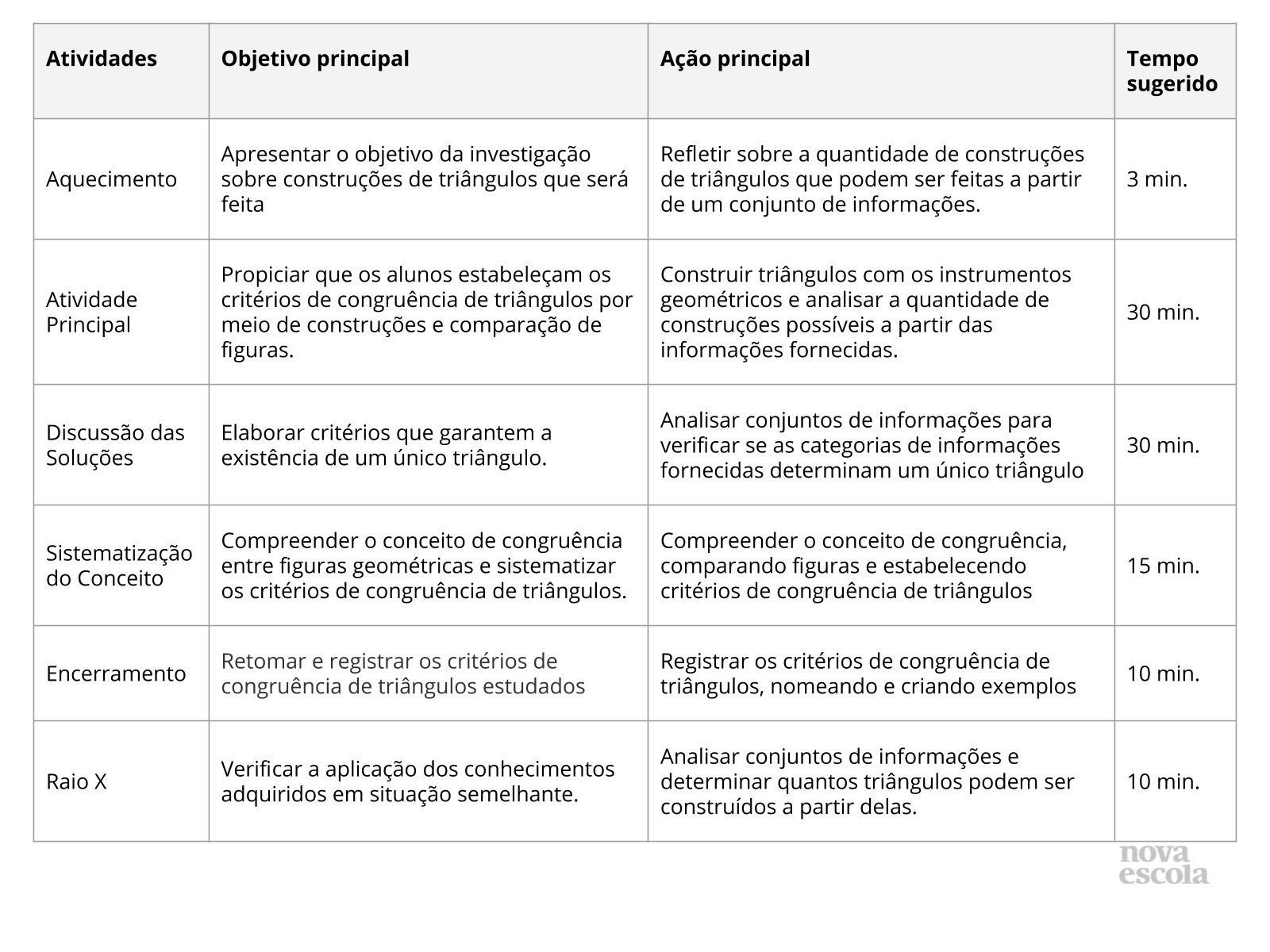
Atividade principal
Plano de Aula
Plano de aula: Elaborando critérios de congruência de triângulos
Plano 5 de uma sequência de 10 planos. Veja todos os planos sobre Transformações isométricas e congruência de triângulos
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Renata Akemi Maekawa
Mentor: Fabricio Eduardo Ferreira
Especialista de área: Pricilla Cerqueira
Habilidade da BNCC
EF08MA12 - Demonstrar propriedades de quadriláteros por meio da identificação da congruência de triângulos.
Objetivos específicos
- Construir triângulos a partir de informações utilizando instrumentos geométricos.
- Analisar a quantidade de possibilidades de construções para cada conjunto de informações fornecidos.
- Elaborar critérios de congruência de triângulos.
- Compreender o conceito de congruência de triângulos
Conceito-chave
Critérios de congruência de triângulos
Recursos necessários
Régua, compasso, transferidor, folhas de sulfite e fichas impressas.
Projetor (se possível)
Habilidades BNCC:
Objetivos de aprendizagem
- Construir triângulos a partir de informações utilizando instrumentos geométricos.
- Analisar a quantidade de possibilidades de construções para cada conjunto de informações fornecidos.
- Elaborar critérios de congruência de triângulos.
- Compreender o conceito de congruência de triângulos
Resumo da Aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientações: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Aquecimento

Tempo sugerido: 3 minutos.
Orientações: Inicie a aula projetando ou lendo a pergunta para a turma. Solicite que alguns alunos compartilhem suas respostas e anote-as no quadro. É possível que apareçam as seguintes respostas: “apenas um triângulo”, “vários triângulos” ou “depende das informações que são fornecidas”. Nesta etapa, não abra para a discussão, pois esta será feita posteriormente.
Propósito: Apresentar o questionamento principal a ser respondido na aula para que o aluno realize as próximas atividades sabendo qual deve ser o foco.
Atividade Principal

Tempo sugerido: 2 minutos.
Orientações: Projete este slide ou leia o texto para os alunos. Verifique se todos lembram os nomes dos instrumentos geométricos, os elementos geométricos relacionados a cada um e os procedimentos de uso. Se possível, tenha em mãos instrumentos geométricos do quadro para exemplificar seus usos.
Propósito: Retomar os nomes e procedimentos de uso dos instrumentos geométricos
Materiais complementares para impressão:
Atividade Principal

Tempo sugerido: 18 minutos (Slides 5 a 10).
Orientações: Organize os alunos em duplas heterogêneas e entregue uma folha de sulfite para cada aluno (tenha em mãos mais folhas, caso os alunos precisem). Projete ou escreva o enunciado da atividade no quadro (texto que está no balão azul) e, em seguida, leia-o para a turma. Os alunos deverão realizar um item por vez individualmente, comparar as figuras obtidas com a dupla e anotar a quantidade de possibilidades. Para isso, projete ou escreva no quadro um item, leia-o e dê 3 minutos para que resolvam cada um. Para exibir o próximo item da atividade, vá para o próximo slide. Solicite que os alunos peçam mais folha de sulfite, caso necessitem.
Oriente que os alunos sobreponham os sulfites para comparar os triângulos construídos, verificando se ficam exatamente iguais ou não. Esta ação favorecerá o estabelecimento de relação entre as transformações geométricas e o conceito de congruência de triângulos.
Nesse momento, circule pela sala para observar as construções e respostas dos alunos, verificando se os alunos lembram como construir triângulos com instrumentos geométricos.
Propósito: Criar condições para que os alunos estabeleçam os critérios de congruência de triângulos por meio de construções geométricas e comparação de figuras.
Atividade Principal

Tempo sugerido: 18 minutos (Slides 5 a 10).
Orientações: Organize os alunos em duplas heterogêneas e entregue uma folha de sulfite para cada aluno (tenha em mãos mais folhas, caso os alunos precisem). Projete ou escreva o enunciado da atividade no quadro (texto que está no balão azul) e, em seguida, leia-o para a turma. Os alunos deverão realizar um item por vez individualmente, comparar as figuras obtidas com a dupla e anotar a quantidade de possibilidades. Para isso, projete ou escreva no quadro um item, leia-o e dê 3 minutos para que resolvam cada um. Para exibir o próximo item da atividade, vá para o próximo slide. Solicite que os alunos peçam mais folha de sulfite, caso necessitem.
Oriente que os alunos sobreponham os sulfites para comparar os triângulos construídos, verificando se ficam exatamente iguais ou não. Esta ação favorecerá o estabelecimento de relação entre as transformações geométricas e o conceito de congruência de triângulos.
Nesse momento, circule pela sala para observar as construções e respostas dos alunos, verificando se os alunos lembram como construir triângulos com instrumentos geométricos.
Propósito: Criar condições para que os alunos estabeleçam os critérios de congruência de triângulos por meio de construções geométricas e comparação de figuras.
Atividade Principal
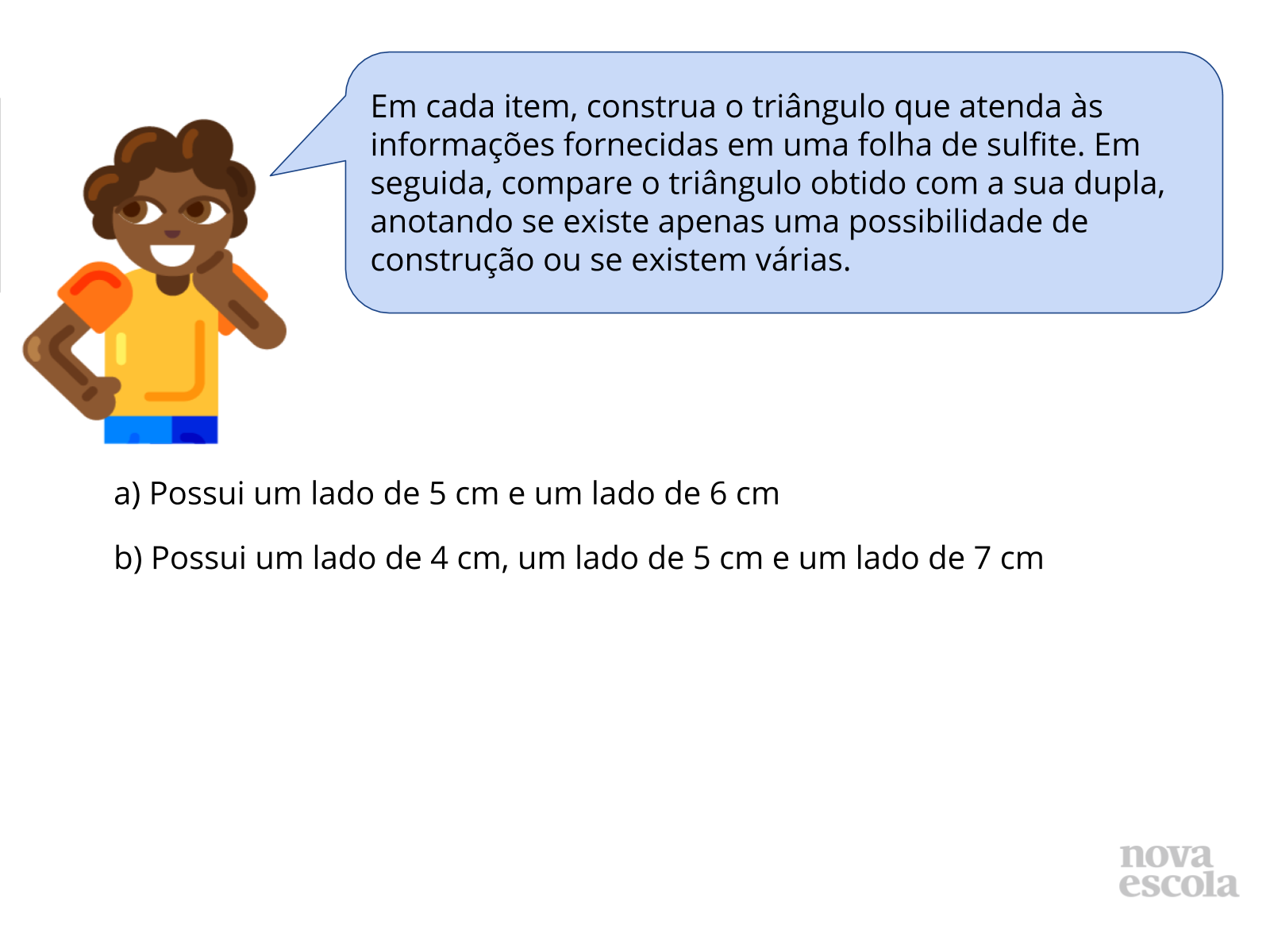
Tempo sugerido: 18 minutos (Slides 5 a 10).
Orientações: Organize os alunos em duplas heterogêneas e entregue uma folha de sulfite para cada aluno (tenha em mãos mais folhas, caso os alunos precisem). Projete ou escreva o enunciado da atividade no quadro (texto que está no balão azul) e, em seguida, leia-o para a turma. Os alunos deverão realizar um item por vez individualmente, comparar as figuras obtidas com a dupla e anotar a quantidade de possibilidades. Para isso, projete ou escreva no quadro um item, leia-o e dê 3 minutos para que resolvam cada um. Para exibir o próximo item da atividade, vá para o próximo slide. Solicite que os alunos peçam mais folha de sulfite, caso necessitem.
Oriente que os alunos sobreponham os sulfites para comparar os triângulos construídos, verificando se ficam exatamente iguais ou não. Esta ação favorecerá o estabelecimento de relação entre as transformações geométricas e o conceito de congruência de triângulos.
Nesse momento, circule pela sala para observar as construções e respostas dos alunos, verificando se os alunos lembram como construir triângulos com instrumentos geométricos.
Propósito: Criar condições para que os alunos estabeleçam os critérios de congruência de triângulos por meio de construções geométricas e comparação de figuras.
Atividade Principal

Tempo sugerido: 18 minutos (Slides 5 a 10).
Orientações: Organize os alunos em duplas heterogêneas e entregue uma folha de sulfite para cada aluno (tenha em mãos mais folhas, caso os alunos precisem). Projete ou escreva o enunciado da atividade no quadro (texto que está no balão azul) e, em seguida, leia-o para a turma. Os alunos deverão realizar um item por vez individualmente, comparar as figuras obtidas com a dupla e anotar a quantidade de possibilidades. Para isso, projete ou escreva no quadro um item, leia-o e dê 3 minutos para que resolvam cada um. Para exibir o próximo item da atividade, vá para o próximo slide. Solicite que os alunos peçam mais folha de sulfite, caso necessitem.
Oriente que os alunos sobreponham os sulfites para comparar os triângulos construídos, verificando se ficam exatamente iguais ou não. Esta ação favorecerá o estabelecimento de relação entre as transformações geométricas e o conceito de congruência de triângulos.
Nesse momento, circule pela sala para observar as construções e respostas dos alunos, verificando se os alunos lembram como construir triângulos com instrumentos geométricos.
Propósito: Criar condições para que os alunos estabeleçam os critérios de congruência de triângulos por meio de construções geométricas e comparação de figuras.
Atividade Principal

Tempo sugerido: 18 minutos (Slides 5 a 10).
Orientações: Organize os alunos em duplas heterogêneas e entregue uma folha de sulfite para cada aluno (tenha em mãos mais folhas, caso os alunos precisem). Projete ou escreva o enunciado da atividade no quadro (texto que está no balão azul) e, em seguida, leia-o para a turma. Os alunos deverão realizar um item por vez individualmente, comparar as figuras obtidas com a dupla e anotar a quantidade de possibilidades. Para isso, projete ou escreva no quadro um item, leia-o e dê 3 minutos para que resolvam cada um. Para exibir o próximo item da atividade, vá para o próximo slide. Solicite que os alunos peçam mais folha de sulfite, caso necessitem.
Oriente que os alunos sobreponham os sulfites para comparar os triângulos construídos, verificando se ficam exatamente iguais ou não. Esta ação favorecerá o estabelecimento de relação entre as transformações geométricas e o conceito de congruência de triângulos.
Nesse momento, circule pela sala para observar as construções e respostas dos alunos, verificando se os alunos lembram como construir triângulos com instrumentos geométricos.
Propósito: Criar condições para que os alunos estabeleçam os critérios de congruência de triângulos por meio de construções geométricas e comparação de figuras.
Atividade Principal

Tempo sugerido: 18 minutos (Slides 5 a 10).
Orientações: Organize os alunos em duplas heterogêneas e entregue uma folha de sulfite para cada aluno (tenha em mãos mais folhas, caso os alunos precisem). Projete ou escreva o enunciado da atividade no quadro (texto que está no balão azul) e, em seguida, leia-o para a turma. Os alunos deverão realizar um item por vez individualmente, comparar as figuras obtidas com a dupla e anotar a quantidade de possibilidades. Para isso, projete ou escreva no quadro um item, leia-o e dê 3 minutos para que resolvam cada um. Para exibir o próximo item da atividade, vá para o próximo slide. Solicite que os alunos peçam mais folha de sulfite, caso necessitem.
Oriente que os alunos sobreponham os sulfites para comparar os triângulos construídos, verificando se ficam exatamente iguais ou não. Esta ação favorecerá o estabelecimento de relação entre as transformações geométricas e o conceito de congruência de triângulos.
Nesse momento, circule pela sala para observar as construções e respostas dos alunos, verificando se os alunos lembram como construir triângulos com instrumentos geométricos.
Propósito: Criar condições para que os alunos estabeleçam os critérios de congruência de triângulos por meio de construções geométricas e comparação de figuras.
Atividade Principal

Tempo sugerido: 10 minutos.
Orientações: Organize os alunos em quartetos (duas duplas do momento anterior). Projete ou escreva o enunciado da atividade no quadro e, em seguida, leia-o para a turma. Solicite que os alunos analisem as construções e anotações feitas e discutam a resposta para a pergunta. Todos os alunos dos quartetos devem registrar as conclusões do grupo em seus cadernos. Nesse momento, circule pela sala para observar discussões dos alunos, sem informar os grupos se a resposta obtida por eles está correta ou não. As discussões coletivas serão feitas posteriormente.
Caso algum grupo termine, analise os conjuntos de informações estabelecidos por eles e proponha que pensem em generalizações desses conjuntos (exemplo: se os alunos estabeleceram que o item c gera um único triângulo, pergunte: “e se fossem outras medidas de lado e outro ângulo, também existiria apenas uma possibilidade?”)
Propósito: Criar condições para que os alunos estabeleçam os critérios de congruência de triângulos por meio de construções geométricas e comparação de figuras.
Discussão das Soluções

Tempo sugerido: 5 minutos.
Orientações: Peça para que os grupos compartilhem as respostas e escreva-as no quadro, explicando que os itens serão discutidos com detalhes em seguida. Caso haja discordância em relação a algum item, faça uma marcação no quadro que seja discutida no momento seguinte.
É provável que os alunos façam referência aos casos específicos apresentados na atividade (exemplo: “é possível construir apenas um triângulo no item b” em vez de “é possível construir apenas um triângulo quando são dadas as medidas de dois lados e do ângulo entre eles”), mas caso os alunos tragam falas generalizadas do segundo tipo, anote-as no quadro também para a discussão que ocorrerá em seguida.
Propósito: Compartilhar hipóteses dos alunos sobre conjuntos de informações que determinam um triângulo único.
Discussão das Soluções
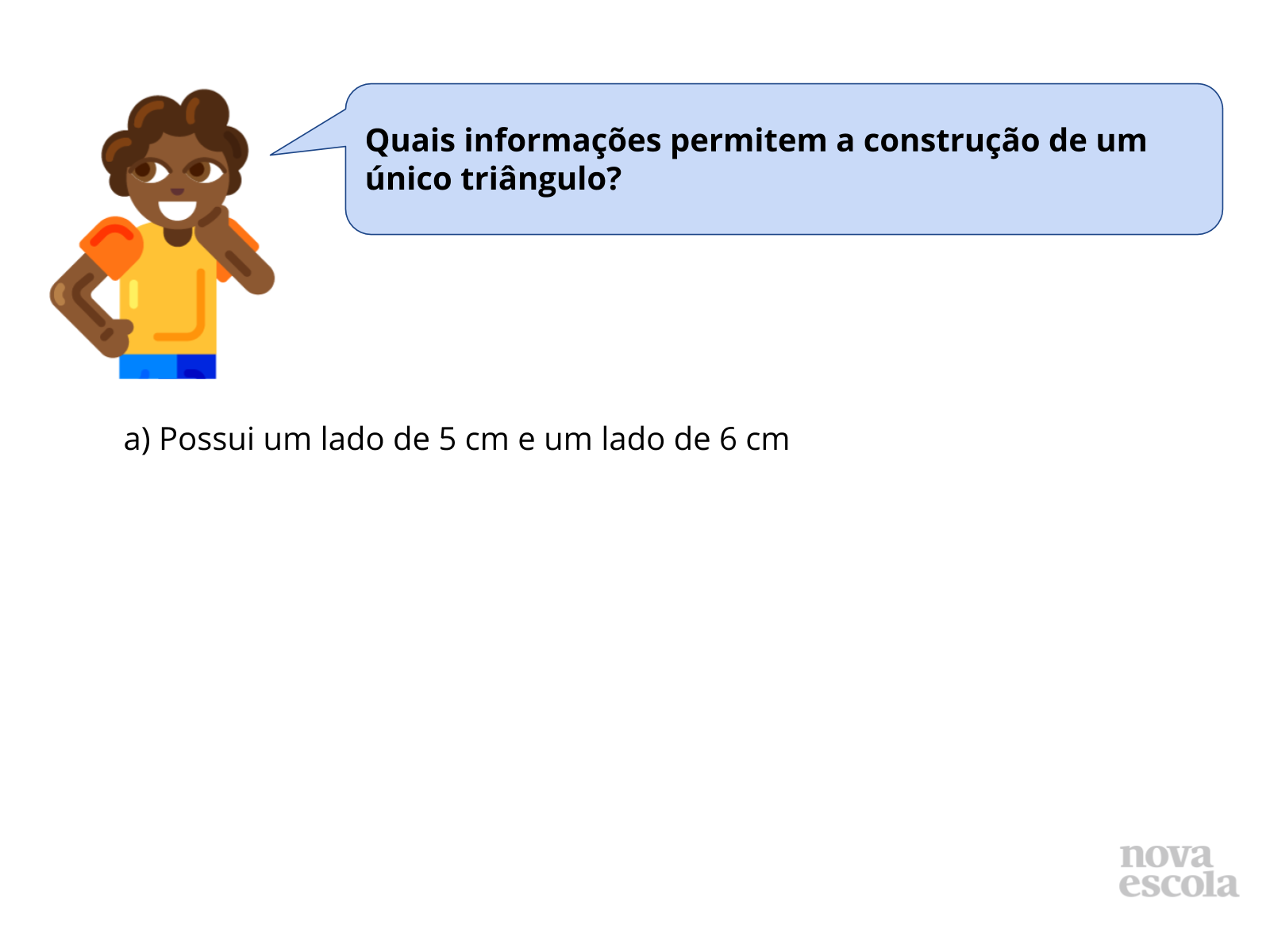
Tempo sugerido: 5 minutos (slides 13 e 14).
Orientações: Caso haja discordância entre os grupos em relação à quantidade de possibilidades de construções que contemplam essas informações, inicie solicitando que um grupo que acredita que existe apenas uma possibilidade compartilhe com a turma a justificativa da resposta. Em seguida (ou caso a turma já concorde que existem várias possibilidades), peça para que um grupo que acredita que existem várias possibilidades compartilhe a resposta. Nesse momento, é interessante que os alunos exibam as diferentes construções que realizaram nos papéis e também façam construções no quadro para compartilhar com a classe. Além disso, é importante que compreendam por que existem infinitas possibilidades de construções a partir das informações fornecidas. A construção aparece no slide 14. Mostre para a turma se julgar necessário.
Propósito: Propiciar que os alunos analisem construções de triângulos para verificar que existem infinitas possibilidades de construções quando são fornecidas apenas as medidas de dois lados de um triângulo.
Discuta com a Turma:
- Que instrumentos geométricos foram necessários para realizar esta construção?
- Quantos triângulos diferentes podem ser construídos com essas informações?
- Que elementos não estão determinados e podem ser escolhidos?
- Sempre que são fornecidas apenas as medidas de dois lados podemos construir infinitos triângulos?
- (se houver tempo, retomar a desigualdade triangular) O outro lado pode assumir qualquer valor?
Discussão das Soluções
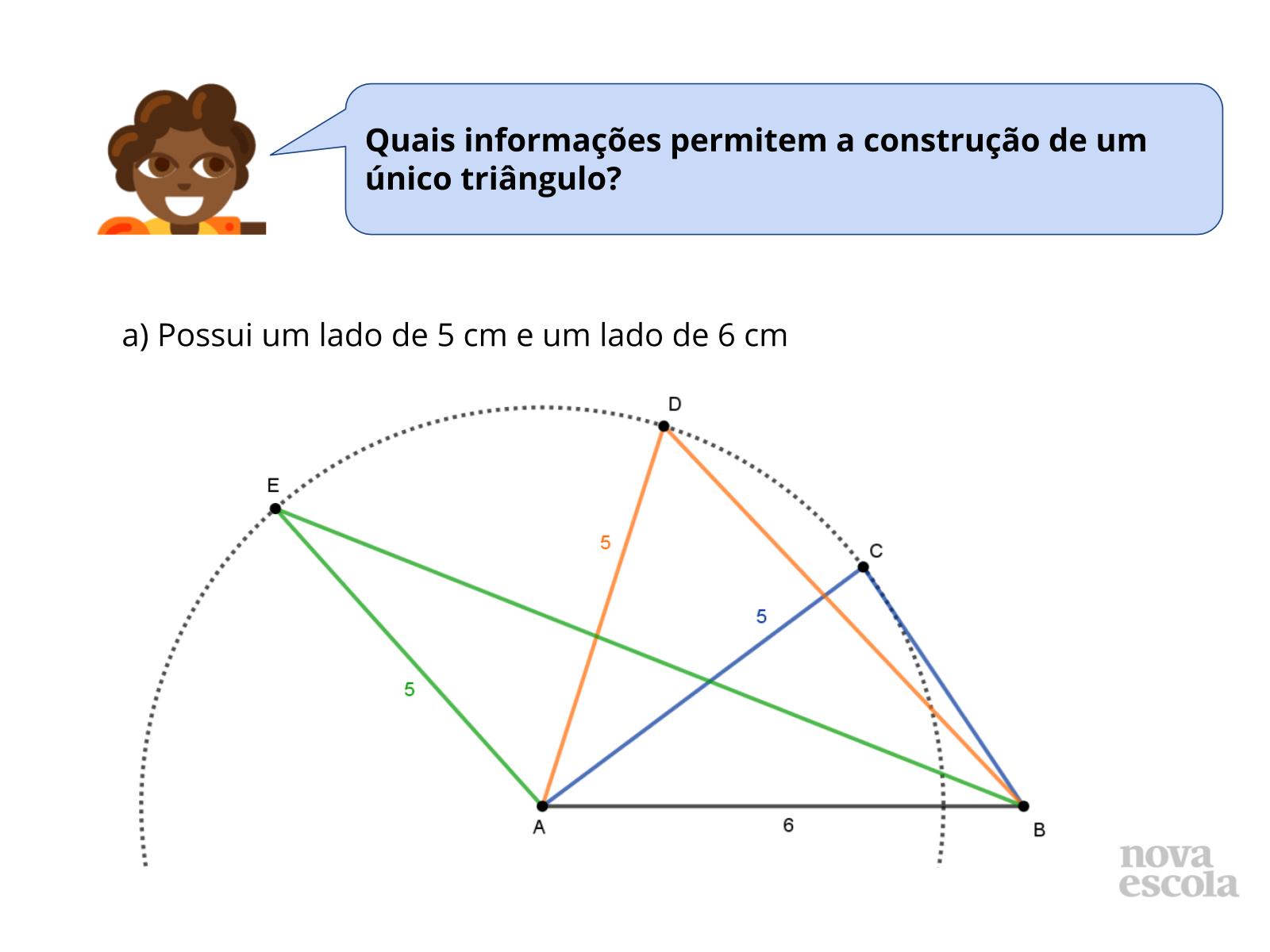
Tempo sugerido: 5 minutos (slides 13 e 14).
Orientações: Caso haja discordância entre os grupos em relação à quantidade de possibilidades de construções que contemplam essas informações, inicie solicitando que um grupo que acredita que existe apenas uma possibilidade compartilhe com a turma a justificativa da resposta. Em seguida (ou caso a turma já concorde que existem várias possibilidades), peça para que um grupo que acredita que existem várias possibilidades compartilhe a resposta. Nesse momento, é interessante que os alunos exibam as diferentes construções que realizaram nos papéis e também façam construções no quadro para compartilhar com a classe. Além disso, é importante que compreendam por que existem infinitas possibilidades de construções a partir das informações fornecidas. A construção aparece no slide 14. Mostre para a turma se julgar necessário.
Propósito: Propiciar que os alunos analisem construções de triângulos para verificar que existem infinitas possibilidades de construções quando são fornecidas apenas as medidas de dois lados de um triângulo.
Discuta com a Turma:
- Que instrumentos geométricos foram necessários para realizar esta construção?
- Quantos triângulos diferentes podem ser construídos com essas informações?
- Que elementos não estão determinados e podem ser escolhidos?
- Sempre que são fornecidas apenas as medidas de dois lados podemos construir infinitos triângulos?
- (se houver tempo, retomar a desigualdade triangular) O outro lado pode assumir qualquer valor?
Discussão das Soluções
Tempo sugerido: 5 minutos (slides 15 e 16).
Orientações: Inicie solicitando que um grupo que acredita que existe apenas uma possibilidade compartilhe com a turma a justificativa da resposta e exiba no quadro os passos para a construção do triângulo (é importante retomar a construção com régua e compasso de triângulos a partir das medidas de seus três lados). Em seguida, se houver, peça para que um grupo que acredita que existem várias possibilidades compartilhe a resposta e depois abra para a turma discuta as soluções apresentadas.
Nessa atividade, é importante que os alunos compreendam que existe apenas uma possibilidade de construção quando são informadas as medidas dos três lados de um triângulo, desde que respeitem a desigualdade triangular. A construção aparece no slide 16. Mostre para a turma, se julgar necessário.
Propósito: Propiciar que os alunos analisem construções de triângulos para verificar que existe apenas uma possibilidade de construção quando são fornecidas as medidas de três lados de um triângulo que respeitam a desigualdade triangular.
Discuta com a Turma:
- Que instrumentos geométricos foram necessários para realizar esta construção?
- Quantos triângulos diferentes podem ser construídos com essas informações? Por quê?
- Sempre que são fornecidas as medidas de três lados podemos construir um único triângulo?
- Por que o terceiro vértice não pode se localizar em outra posição?
Discussão das Soluções
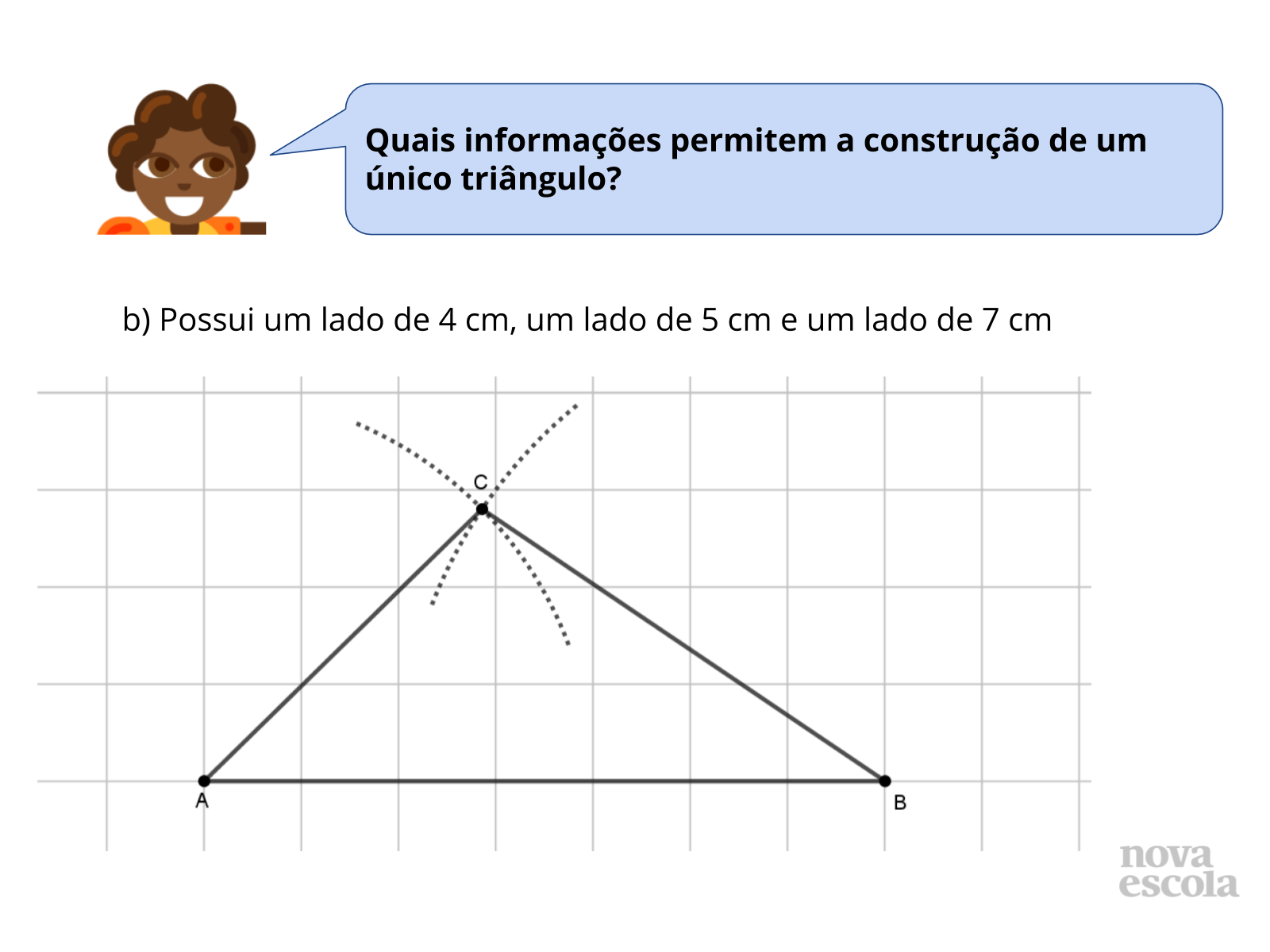
Tempo sugerido: 5 minutos (slides 15 e 16).
Orientações: Inicie solicitando que um grupo que acredita que existe apenas uma possibilidade compartilhe com a turma a justificativa da resposta e exiba no quadro os passos para a construção do triângulo (é importante retomar a construção com régua e compasso de triângulos a partir das medidas de seus três lados). Em seguida, se houver, peça para que um grupo que acredita que existem várias possibilidades compartilhe a resposta e depois abra para a turma discuta as soluções apresentadas.
Nessa atividade, é importante que os alunos compreendam que existe apenas uma possibilidade de construção quando são informadas as medidas dos três lados de um triângulo, desde que respeitem a desigualdade triangular. A construção aparece no slide 16. Mostre para a turma, se julgar necessário.
Propósito: Propiciar que os alunos analisem construções de triângulos para verificar que existe apenas uma possibilidade de construção quando são fornecidas as medidas de três lados de um triângulo que respeitam a desigualdade triangular.
Discuta com a Turma:
- Que instrumentos geométricos foram necessários para realizar esta construção?
- Quantos triângulos diferentes podem ser construídos com essas informações? Por quê?
- Sempre que são fornecidas as medidas de três lados podemos construir um único triângulo?
- Por que o terceiro vértice não pode se localizar em outra posição?
Discussão das Soluções
Tempo sugerido: 5 minutos (slides 17 e 18).
Orientações: Inicie solicitando que um grupo que acredita que existe apenas uma possibilidade compartilhe com a turma a justificativa da resposta e exiba no quadro os passos para a construção do triângulo (é importante retomar a construção com régua e transferidor de triângulos a partir das medidas de dois lados e do ângulo entre eles, explicitando as relações entre os instrumentos geométricos utilizados e os elementos geométricos construídos com cada um). Em seguida, se houver, peça para que um grupo que acredita que existem várias possibilidades compartilhe a resposta e depois abra para a turma discuta as soluções apresentadas. Nessa atividade, é importante que os alunos compreendam que existe apenas uma possibilidade de construção de triângulo quando são informadas as medidas de dois lados e do ângulo entre eles. A construção aparece no slide 18. Mostre para a turma se julgar necessário.
Propósito: Propiciar que os alunos analisem construções de triângulos para verificar que existe apenas uma possibilidade de construção de triângulo quando são fornecidas as medidas de dois lados e do ângulo entre eles.
Discuta com a Turma:
- Que instrumentos geométricos foram necessários para realizar esta construção?
- Quantos triângulos diferentes podem ser construídos com essas informações? Por quê?
- Sempre que são fornecidas as medidas de dois lados e do ângulo entre eles podemos construir um único triângulo?
- Por que o terceiro vértice não pode se localizar em outra posição?
Discussão das Soluções
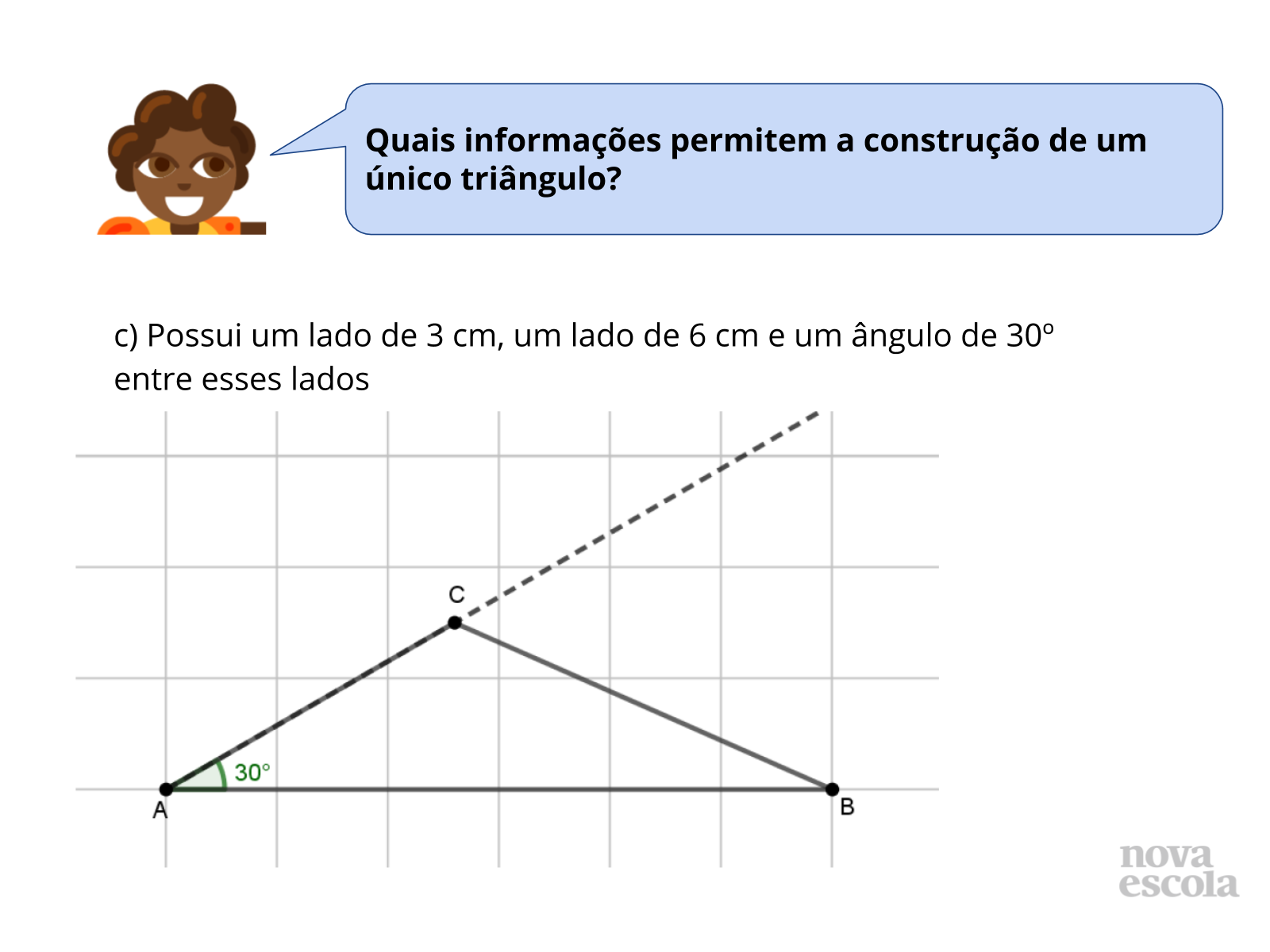
Tempo sugerido: 5 minutos (slides 17 e 18).
Orientações: Inicie solicitando que um grupo que acredita que existe apenas uma possibilidade compartilhe com a turma a justificativa da resposta e exiba no quadro os passos para a construção do triângulo (é importante retomar a construção com régua e transferidor de triângulos a partir das medidas de dois lados e do ângulo entre eles, explicitando as relações entre os instrumentos geométricos utilizados e os elementos geométricos construídos com cada um). Em seguida, se houver, peça para que um grupo que acredita que existem várias possibilidades compartilhe a resposta e depois abra para a turma discuta as soluções apresentadas. Nessa atividade, é importante que os alunos compreendam que existe apenas uma possibilidade de construção de triângulo quando são informadas as medidas de dois lados e do ângulo entre eles. A construção aparece no slide 18. Mostre para a turma se julgar necessário.
Propósito: Propiciar que os alunos analisem construções de triângulos para verificar que existe apenas uma possibilidade de construção de triângulo quando são fornecidas as medidas de dois lados e do ângulo entre eles.
Discuta com a Turma:
- Que instrumentos geométricos foram necessários para realizar esta construção?
- Quantos triângulos diferentes podem ser construídos com essas informações? Por quê?
- Sempre que são fornecidas as medidas de dois lados e do ângulo entre eles podemos construir um único triângulo?
- Por que o terceiro vértice não pode se localizar em outra posição?
Discussão das Soluções
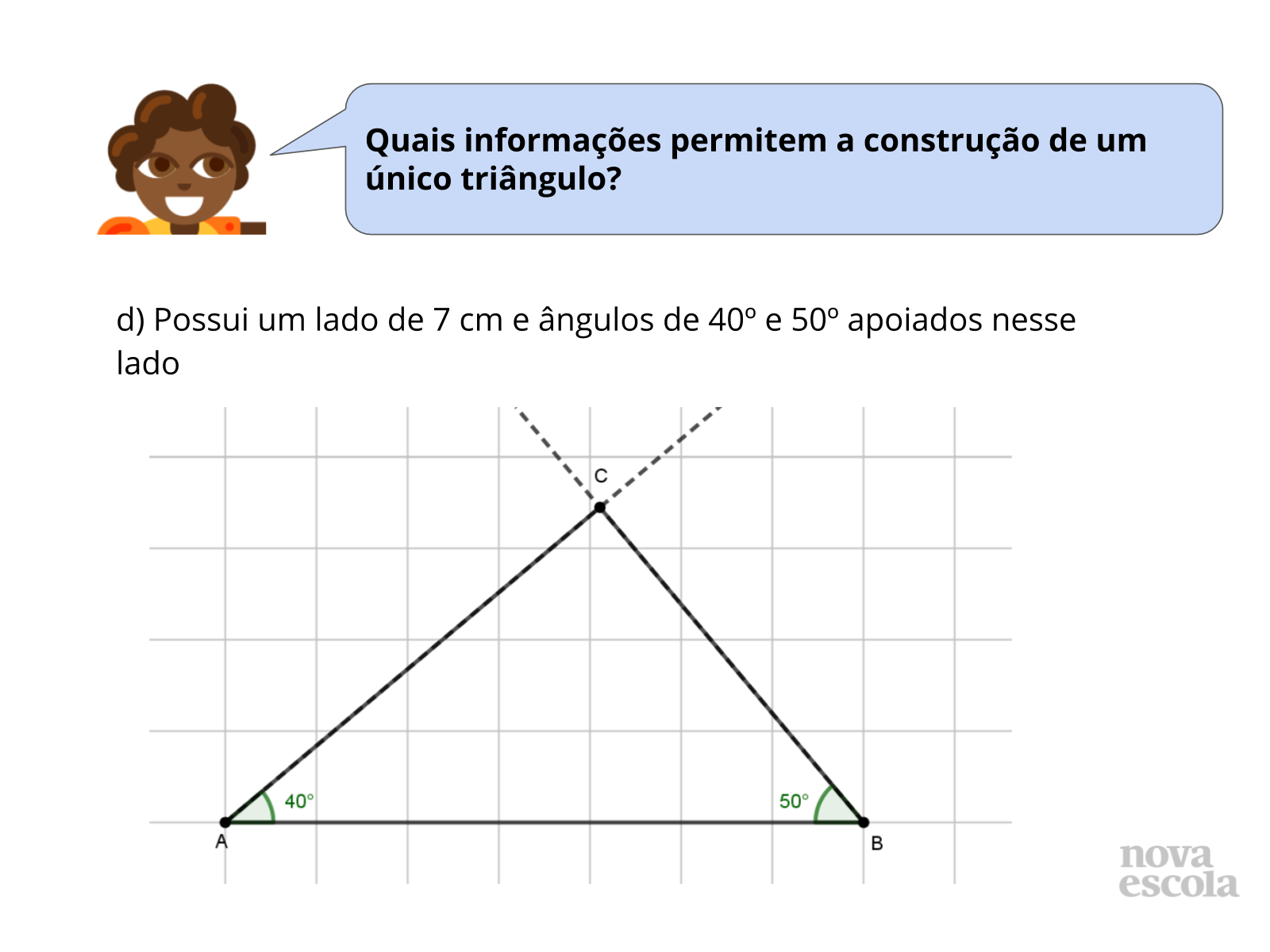
Tempo sugerido: 5 minutos (slides 19 e 20).
Orientações: Inicie solicitando que um grupo que acredita que existe apenas uma possibilidade compartilhe com a turma a justificativa da resposta e exiba no quadro os passos para a construção do triângulo (é importante retomar a construção com régua e transferidor de triângulos a partir das medidas de um lado e dos dois ângulos adjacentes a ele). Em seguida, se houver, peça para que um grupo que acredita que existem várias possibilidades compartilhe a resposta e depois abra para a turma discuta as soluções apresentadas.
Nessa atividade, é importante que os alunos compreendam que existe apenas uma possibilidade de construção de triângulo quando são informadas as medidas de um lado e dos dois ângulos apoiados nele.
A construção aparece no slide 20. Mostre para a turma se julgar necessário.
Propósito: Propiciar que os alunos analisem construções de triângulos para verificar que existe apenas uma possibilidade de construção de triângulo quando são fornecidas as medidas de um lado e dos dois ângulos apoiados nele.
Discuta com a Turma:
- Que instrumentos geométricos foram necessários para realizar esta construção?
- Quantos triângulos diferentes podem ser construídos com essas informações? Por quê?
- Sempre que são fornecidas as medidas de um lado e dos dois ângulos apoiados nele podemos construir um único triângulo?
- Por que o terceiro vértice não pode se localizar em outra posição?
Discussão das Soluções
Tempo sugerido: 5 minutos (slides 19 e 20).
Orientações: Inicie solicitando que um grupo que acredita que existe apenas uma possibilidade compartilhe com a turma a justificativa da resposta e exiba no quadro os passos para a construção do triângulo (é importante retomar a construção com régua e transferidor de triângulos a partir das medidas de um lado e dos dois ângulos adjacentes a ele). Em seguida, se houver, peça para que um grupo que acredita que existem várias possibilidades compartilhe a resposta e depois abra para a turma discuta as soluções apresentadas.
Nessa atividade, é importante que os alunos compreendam que existe apenas uma possibilidade de construção de triângulo quando são informadas as medidas de um lado e dos dois ângulos apoiados nele.
A construção aparece no slide 20. Mostre para a turma se julgar necessário.
Propósito: Propiciar que os alunos analisem construções de triângulos para verificar que existe apenas uma possibilidade de construção de triângulo quando são fornecidas as medidas de um lado e dos dois ângulos apoiados nele.
Discuta com a Turma:
- Que instrumentos geométricos foram necessários para realizar esta construção?
- Quantos triângulos diferentes podem ser construídos com essas informações? Por quê?
- Sempre que são fornecidas as medidas de um lado e dos dois ângulos apoiados nele podemos construir um único triângulo?
- Por que o terceiro vértice não pode se localizar em outra posição?
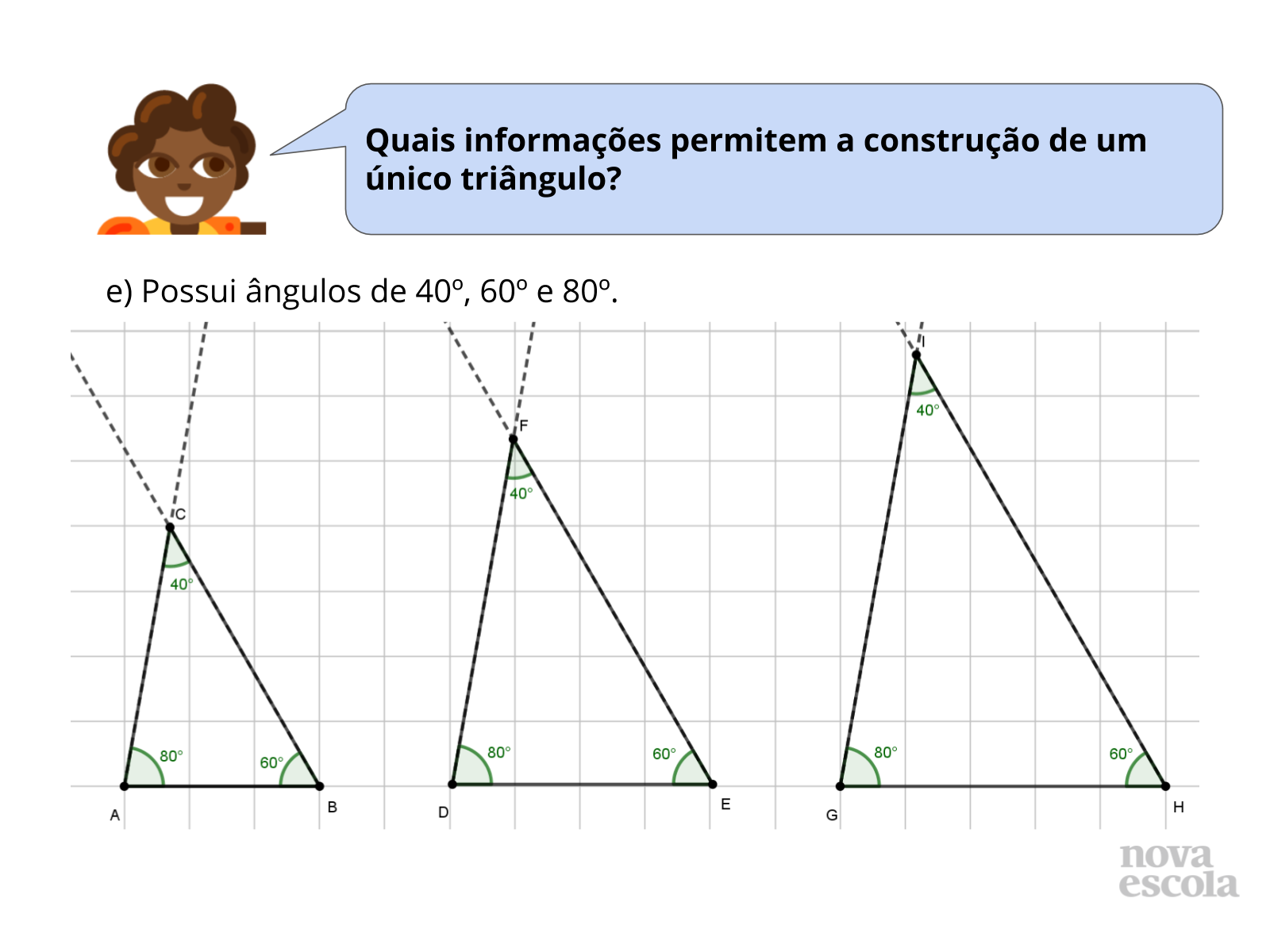
Discussão das Soluções
Tempo sugerido: 5 minutos (slides 21 e 22).
Orientações: Caso haja discordância entre os grupos em relação à quantidade de possibilidades de construções que contemplam essas informações, inicie solicitando que um grupo que acredita que existe apenas uma possibilidade compartilhe com a turma a justificativa da resposta. Em seguida (ou caso a turma já concorde que existem várias possibilidades), peça para que um grupo que acredita que existem várias possibilidades compartilhe a resposta. Nesse momento, é interessante que os alunos exibam as diferentes construções que realizaram nos papéis e também façam construções no quadro para compartilhar com a classe. Além disso, é importante que compreendam por que existem infinitas possibilidades de construções a partir das informações fornecidas.
É interessante comentar que os triângulos construídos são semelhantes e que os alunos estudarão esse conceito no próximo ano escolar.
A construção aparece no slide 22. Mostre para a turma se julgar necessário.
Propósito: Propiciar que os alunos analisem construções de triângulos para verificar que existem infinitas possibilidades de construções quando são fornecidas apenas as medidas dos ângulos de um triângulo.
Discuta com a Turma:
- Que instrumentos geométricos foram necessários para realizar esta construção?
- Quantos triângulos diferentes podem ser construídos com essas informações?
- Que elementos não estão determinados e podem ser escolhidos?
- Sempre que são fornecidas apenas as medidas dos três ângulos podemos construir infinitos triângulos?
- (se houver tempo, retomar a soma dos ângulos internos de um triângulo) Quaisquer três medidas podem representar os ângulos internos de um triângulo?
Discussão das Soluções
Tempo sugerido: 5 minutos (slides 21 e 22).
Orientações: Caso haja discordância entre os grupos em relação à quantidade de possibilidades de construções que contemplam essas informações, inicie solicitando que um grupo que acredita que existe apenas uma possibilidade compartilhe com a turma a justificativa da resposta. Em seguida (ou caso a turma já concorde que existem várias possibilidades), peça para que um grupo que acredita que existem várias possibilidades compartilhe a resposta. Nesse momento, é interessante que os alunos exibam as diferentes construções que realizaram nos papéis e também façam construções no quadro para compartilhar com a classe. Além disso, é importante que compreendam por que existem infinitas possibilidades de construções a partir das informações fornecidas.
É interessante comentar que os triângulos construídos são semelhantes e que os alunos estudarão esse conceito no próximo ano escolar.
A construção aparece no slide 22. Mostre para a turma se julgar necessário.
Propósito: Propiciar que os alunos analisem construções de triângulos para verificar que existem infinitas possibilidades de construções quando são fornecidas apenas as medidas dos ângulos de um triângulo.
Discuta com a Turma:
- Que instrumentos geométricos foram necessários para realizar esta construção?
- Quantos triângulos diferentes podem ser construídos com essas informações?
- Que elementos não estão determinados e podem ser escolhidos?
- Sempre que são fornecidas apenas as medidas dos três ângulos podemos construir infinitos triângulos?
- (se houver tempo, retomar a soma dos ângulos internos de um triângulo) Quaisquer três medidas podem representar os ângulos internos de um triângulo?
Sistematização do Conceito

Tempo sugerido: 10 minutos (slides 23 a 32).
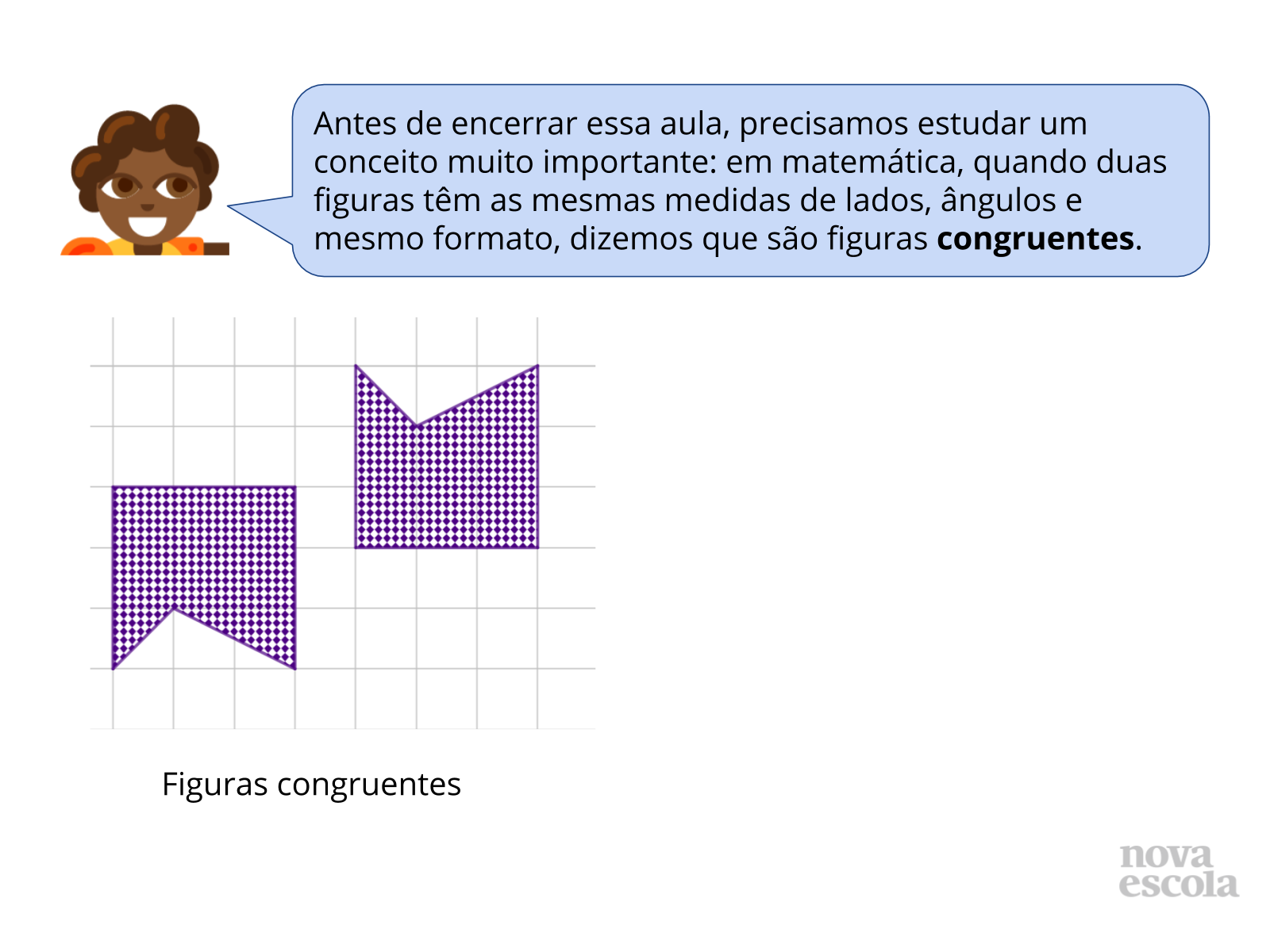
Orientações: Projete este slide ou leia o texto para os alunos. Construa alguns exemplos de figuras congruentes no quadro ou utilize a imagem do slide para a exploração. É importante apresentar exemplos de figuras não congruentes também, para explicitar as características que definem a congruência.
Exiba o slide 24 e peça para que a classe diga se as figuras são ou não congruentes, e depois vá para o próximo slide para mostrar a resposta. O próximo par de figuras aparecerá no slide seguinte. Para encerrar esta etapa, utilize o slide 32 para introduzir o símbolo matemático de congruência.
Caso os alunos notem que as figuras congruentes podem ser levadas uma às outras por meio de transformações isométricas, é interessante inserir esse tópico na discussão. Uma exploração mais profunda sobre as relações entre figuras congruentes e transformações isométricas será feita em outro plano desta unidade.
Propósito: Apresentar o conceito de congruência de figuras geométricas e analisar figuras a fim de identificar congruência entre elas.
Sistematização do Conceito

Tempo sugerido: 10 minutos (slides 23 a 32).
Orientações: Projete este slide ou leia o texto para os alunos. Construa alguns exemplos de figuras congruentes no quadro ou utilize a imagem do slide para a exploração. É importante apresentar exemplos de figuras não congruentes também, para explicitar as características que definem a congruência.
Exiba o slide 24 e peça para que a classe diga se as figuras são ou não congruentes, e depois vá para o próximo slide para mostrar a resposta. O próximo par de figuras aparecerá no slide seguinte. Para encerrar esta etapa, utilize o slide 32 para introduzir o símbolo matemático de congruência.
Caso os alunos notem que as figuras congruentes podem ser levadas uma às outras por meio de transformações isométricas, é interessante inserir esse tópico na discussão. Uma exploração mais profunda sobre as relações entre figuras congruentes e transformações isométricas será feita em outro plano desta unidade.
Propósito: Apresentar o conceito de congruência de figuras geométricas e analisar figuras a fim de identificar congruência entre elas.
Sistematização do Conceito
Tempo sugerido: 10 minutos (slides 23 a 32).
Orientações: Projete este slide ou leia o texto para os alunos. Construa alguns exemplos de figuras congruentes no quadro ou utilize a imagem do slide para a exploração. É importante apresentar exemplos de figuras não congruentes também, para explicitar as características que definem a congruência.
Exiba o slide 24 e peça para que a classe diga se as figuras são ou não congruentes, e depois vá para o próximo slide para mostrar a resposta. O próximo par de figuras aparecerá no slide seguinte. Para encerrar esta etapa, utilize o slide 32 para introduzir o símbolo matemático de congruência.
Caso os alunos notem que as figuras congruentes podem ser levadas uma às outras por meio de transformações isométricas, é interessante inserir esse tópico na discussão. Uma exploração mais profunda sobre as relações entre figuras congruentes e transformações isométricas será feita em outro plano desta unidade.
Propósito: Apresentar o conceito de congruência de figuras geométricas e analisar figuras a fim de identificar congruência entre elas.
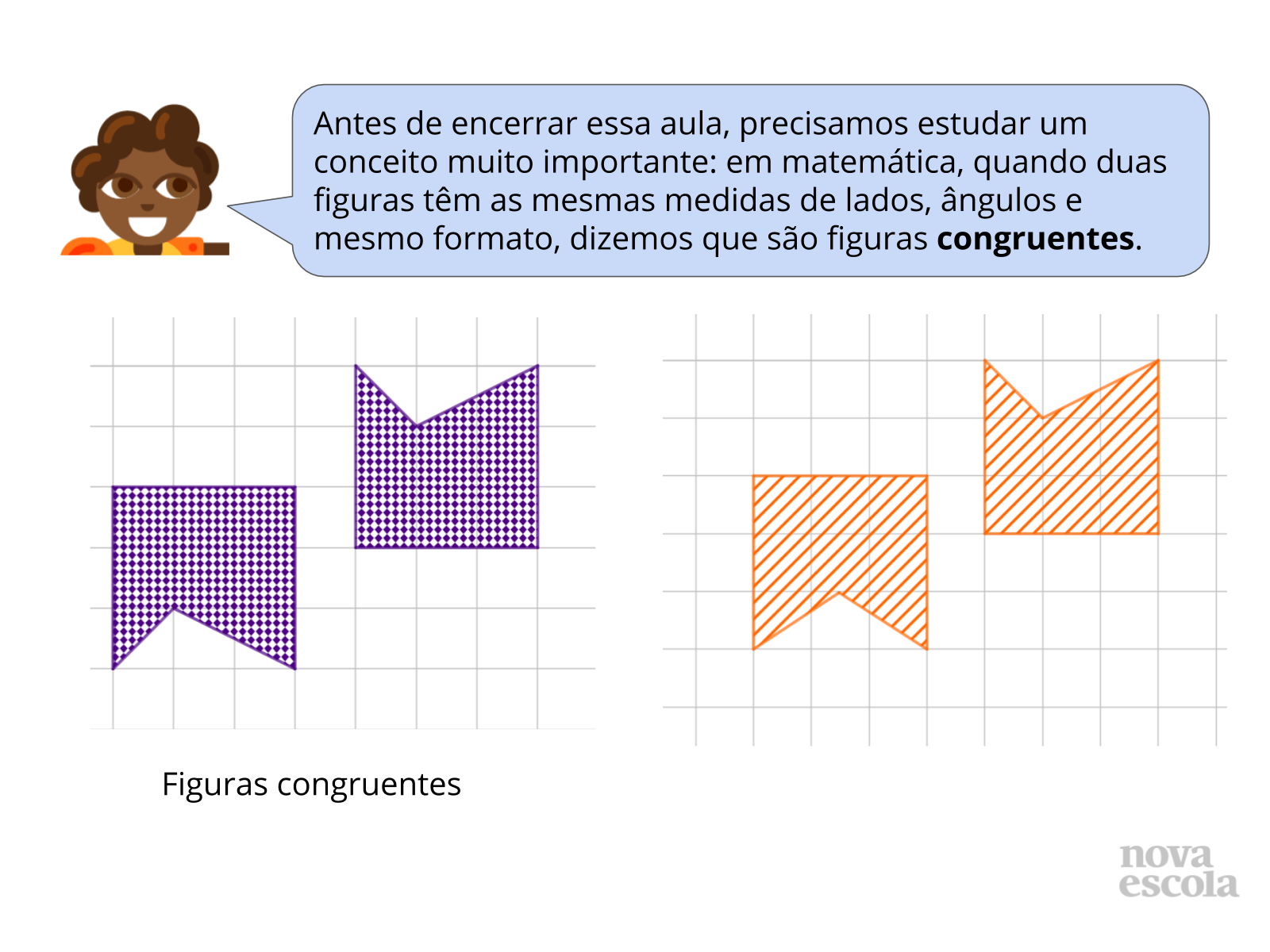
Sistematização do Conceito
Tempo sugerido: 10 minutos (slides 23 a 32).
Orientações: Projete este slide ou leia o texto para os alunos. Construa alguns exemplos de figuras congruentes no quadro ou utilize a imagem do slide para a exploração. É importante apresentar exemplos de figuras não congruentes também, para explicitar as características que definem a congruência.
Exiba o slide 24 e peça para que a classe diga se as figuras são ou não congruentes, e depois vá para o próximo slide para mostrar a resposta. O próximo par de figuras aparecerá no slide seguinte. Para encerrar esta etapa, utilize o slide 32 para introduzir o símbolo matemático de congruência.
Caso os alunos notem que as figuras congruentes podem ser levadas uma às outras por meio de transformações isométricas, é interessante inserir esse tópico na discussão. Uma exploração mais profunda sobre as relações entre figuras congruentes e transformações isométricas será feita em outro plano desta unidade.
Propósito: Apresentar o conceito de congruência de figuras geométricas e analisar figuras a fim de identificar congruência entre elas.
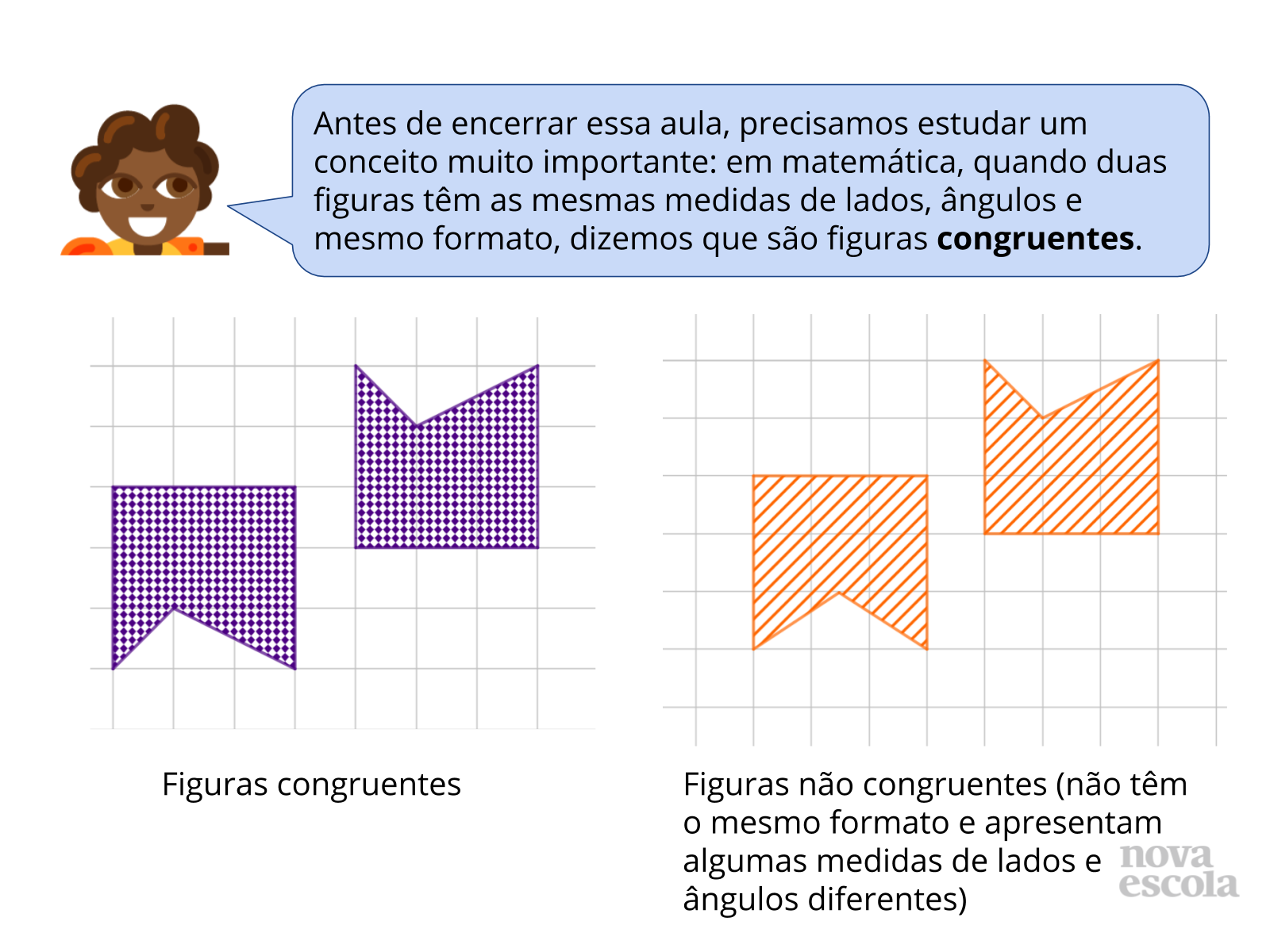
Sistematização do Conceito
Tempo sugerido: 10 minutos (slides 23 a 32).
Orientações: Projete este slide ou leia o texto para os alunos. Construa alguns exemplos de figuras congruentes no quadro ou utilize a imagem do slide para a exploração. É importante apresentar exemplos de figuras não congruentes também, para explicitar as características que definem a congruência.
Exiba o slide 24 e peça para que a classe diga se as figuras são ou não congruentes, e depois vá para o próximo slide para mostrar a resposta. O próximo par de figuras aparecerá no slide seguinte. Para encerrar esta etapa, utilize o slide 32 para introduzir o símbolo matemático de congruência.
Caso os alunos notem que as figuras congruentes podem ser levadas uma às outras por meio de transformações isométricas, é interessante inserir esse tópico na discussão. Uma exploração mais profunda sobre as relações entre figuras congruentes e transformações isométricas será feita em outro plano desta unidade.
Propósito: Apresentar o conceito de congruência de figuras geométricas e analisar figuras a fim de identificar congruência entre elas.
Sistematização do Conceito
Tempo sugerido: 10 minutos (slides 23 a 32).
Orientações: Projete este slide ou leia o texto para os alunos. Construa alguns exemplos de figuras congruentes no quadro ou utilize a imagem do slide para a exploração. É importante apresentar exemplos de figuras não congruentes também, para explicitar as características que definem a congruência.
Exiba o slide 24 e peça para que a classe diga se as figuras são ou não congruentes, e depois vá para o próximo slide para mostrar a resposta. O próximo par de figuras aparecerá no slide seguinte. Para encerrar esta etapa, utilize o slide 32 para introduzir o símbolo matemático de congruência.
Caso os alunos notem que as figuras congruentes podem ser levadas uma às outras por meio de transformações isométricas, é interessante inserir esse tópico na discussão. Uma exploração mais profunda sobre as relações entre figuras congruentes e transformações isométricas será feita em outro plano desta unidade.
Propósito: Apresentar o conceito de congruência de figuras geométricas e analisar figuras a fim de identificar congruência entre elas.
Sistematização do Conceito
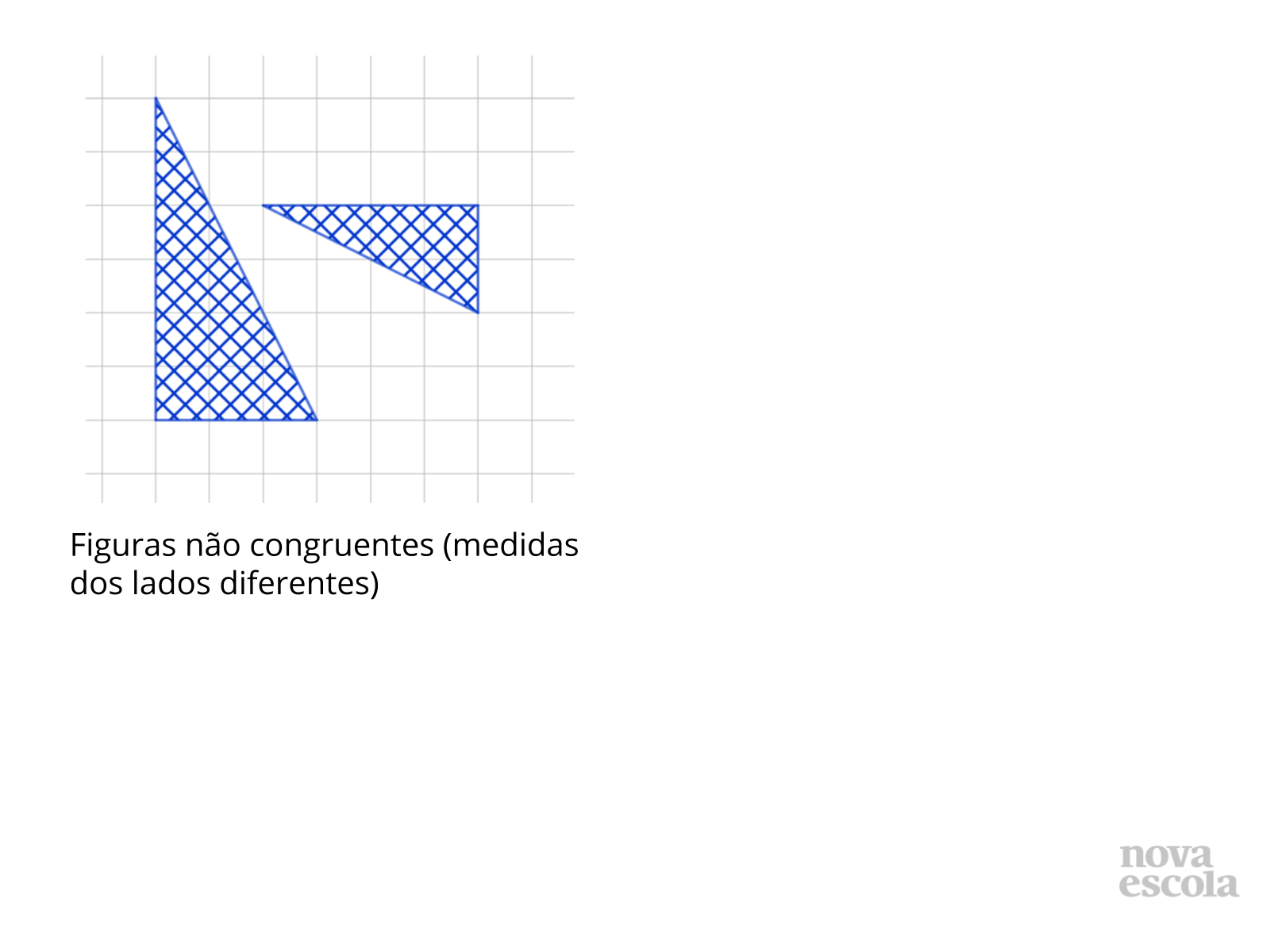
Tempo sugerido: 10 minutos (slides 23 a 32).
Orientações: Projete este slide ou leia o texto para os alunos. Construa alguns exemplos de figuras congruentes no quadro ou utilize a imagem do slide para a exploração. É importante apresentar exemplos de figuras não congruentes também, para explicitar as características que definem a congruência.
Exiba o slide 24 e peça para que a classe diga se as figuras são ou não congruentes, e depois vá para o próximo slide para mostrar a resposta. O próximo par de figuras aparecerá no slide seguinte. Para encerrar esta etapa, utilize o slide 32 para introduzir o símbolo matemático de congruência.
Caso os alunos notem que as figuras congruentes podem ser levadas uma às outras por meio de transformações isométricas, é interessante inserir esse tópico na discussão. Uma exploração mais profunda sobre as relações entre figuras congruentes e transformações isométricas será feita em outro plano desta unidade.
Propósito: Apresentar o conceito de congruência de figuras geométricas e analisar figuras a fim de identificar congruência entre elas.
Sistematização do Conceito
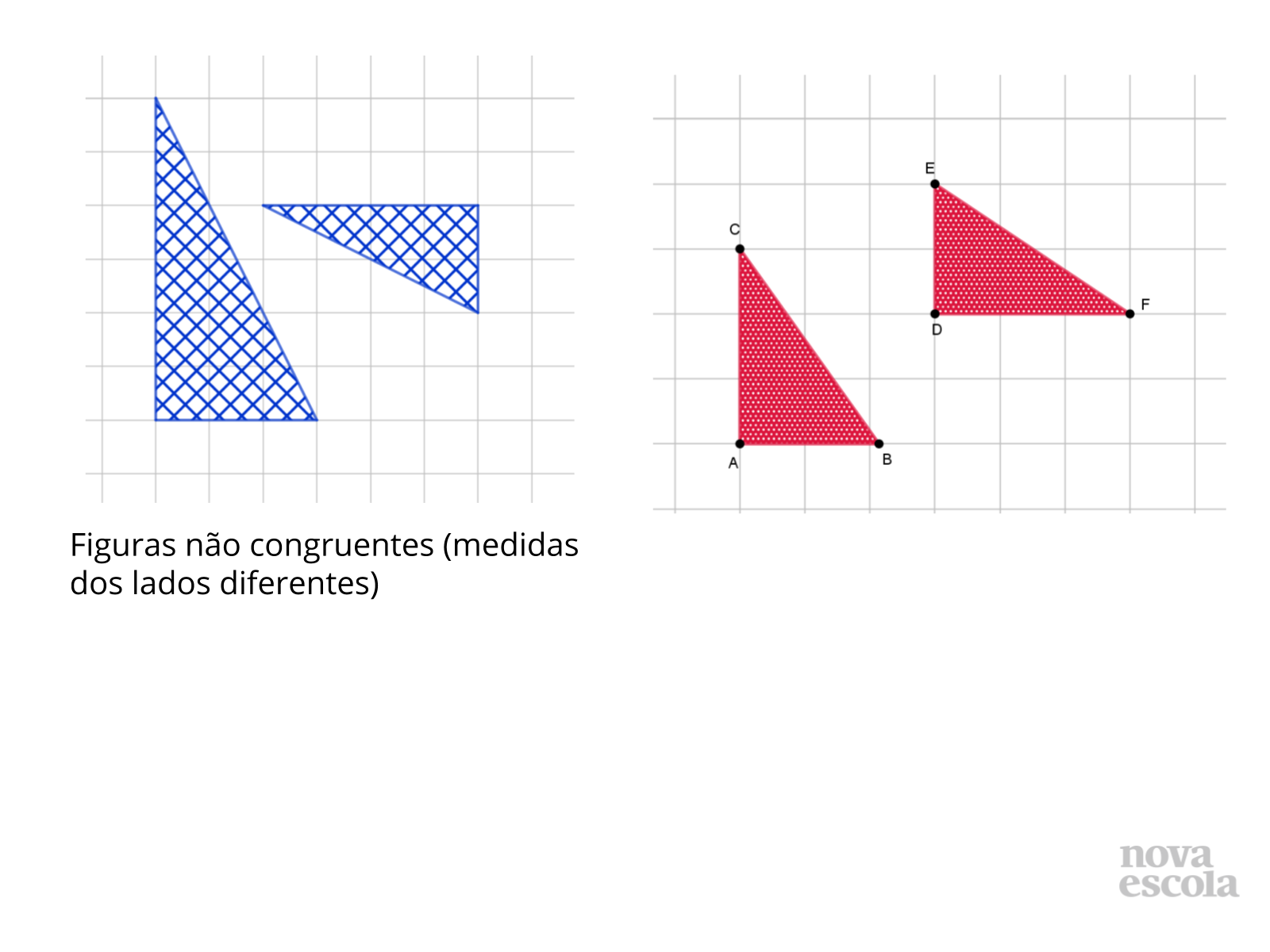
Tempo sugerido: 10 minutos (slides 23 a 32).
Orientações: Projete este slide ou leia o texto para os alunos. Construa alguns exemplos de figuras congruentes no quadro ou utilize a imagem do slide para a exploração. É importante apresentar exemplos de figuras não congruentes também, para explicitar as características que definem a congruência.
Exiba o slide 24 e peça para que a classe diga se as figuras são ou não congruentes, e depois vá para o próximo slide para mostrar a resposta. O próximo par de figuras aparecerá no slide seguinte. Para encerrar esta etapa, utilize o slide 32 para introduzir o símbolo matemático de congruência.
Caso os alunos notem que as figuras congruentes podem ser levadas uma às outras por meio de transformações isométricas, é interessante inserir esse tópico na discussão. Uma exploração mais profunda sobre as relações entre figuras congruentes e transformações isométricas será feita em outro plano desta unidade.
Propósito: Apresentar o conceito de congruência de figuras geométricas e analisar figuras a fim de identificar congruência entre elas.
Sistematização do Conceito
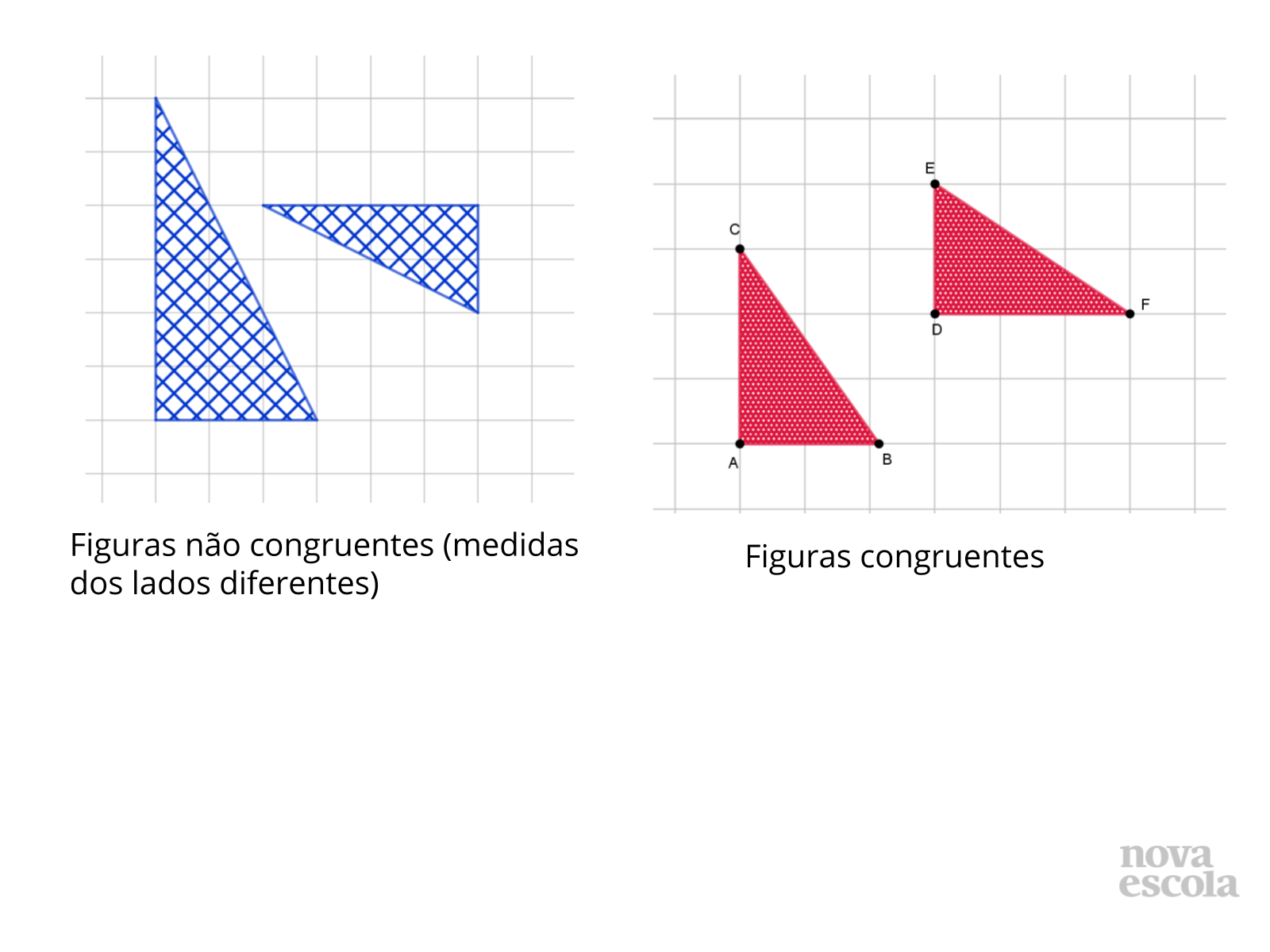
Tempo sugerido: 10 minutos (slides 23 a 32).
Orientações: Projete este slide ou leia o texto para os alunos. Construa alguns exemplos de figuras congruentes no quadro ou utilize a imagem do slide para a exploração. É importante apresentar exemplos de figuras não congruentes também, para explicitar as características que definem a congruência.
Exiba o slide 24 e peça para que a classe diga se as figuras são ou não congruentes, e depois vá para o próximo slide para mostrar a resposta. O próximo par de figuras aparecerá no slide seguinte. Para encerrar esta etapa, utilize o slide 32 para introduzir o símbolo matemático de congruência.
Caso os alunos notem que as figuras congruentes podem ser levadas uma às outras por meio de transformações isométricas, é interessante inserir esse tópico na discussão. Uma exploração mais profunda sobre as relações entre figuras congruentes e transformações isométricas será feita em outro plano desta unidade.
Propósito: Apresentar o conceito de congruência de figuras geométricas e analisar figuras a fim de identificar congruência entre elas.
Sistematização do Conceito
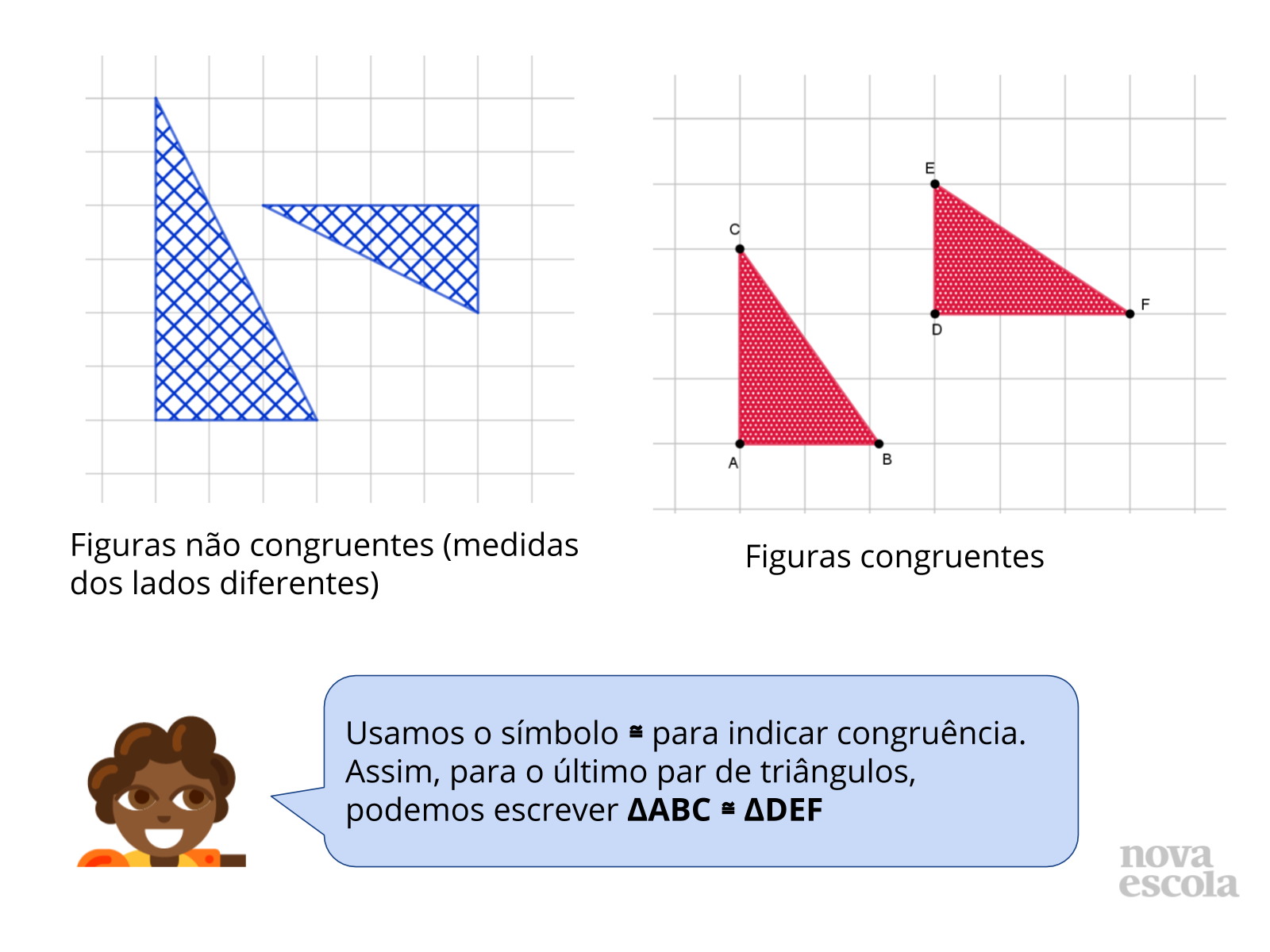
Tempo sugerido: 10 minutos (slides 23 a 32).
Orientações: Projete este slide ou leia o texto para os alunos. Construa alguns exemplos de figuras congruentes no quadro ou utilize a imagem do slide para a exploração. É importante apresentar exemplos de figuras não congruentes também, para explicitar as características que definem a congruência.
Exiba o slide 24 e peça para que a classe diga se as figuras são ou não congruentes, e depois vá para o próximo slide para mostrar a resposta. O próximo par de figuras aparecerá no slide seguinte. Para encerrar esta etapa, utilize o slide 32 para introduzir o símbolo matemático de congruência.
Caso os alunos notem que as figuras congruentes podem ser levadas uma às outras por meio de transformações isométricas, é interessante inserir esse tópico na discussão. Uma exploração mais profunda sobre as relações entre figuras congruentes e transformações isométricas será feita em outro plano desta unidade.
Propósito: Apresentar o conceito de congruência de figuras geométricas e analisar figuras a fim de identificar congruência entre elas.
Sistematização do Conceito
Tempo sugerido: 5 minutos (slides 33 e 35).
Orientações: Leia o primeiro parágrafo do texto e solicite que os alunos digam quais foram os conjuntos de informações vistos em aula que determinam um único triângulo. Se tiver o recurso de projeção, vá para o próximo slide para que os tópicos apareçam. Se não, você pode anotá-los no quadro. Em seguida, peça para que os alunos pensem em siglas que poderiam ser usadas para representar esses três critérios e, depois, vá para o slide 35 para que o segundo balão de fala apareça. Leia o texto com os alunos e verifique se eles têm alguma dúvida sobre o assunto.
É importante que os alunos compreendam que se dois triângulos têm algum desses conjuntos de elementos em comum, então fica garantido que os triângulos são congruentes, ou seja, que possuem lados e ângulos de mesma medida.
Propósito: Relacionar os resultados da investigação feita em aula e o conceito de congruência e critérios de congruência de triângulos .
Sistematização do Conceito

Tempo sugerido: 5 minutos (slides 33 e 35).
Orientações: Leia o primeiro parágrafo do texto e solicite que os alunos digam quais foram os conjuntos de informações vistos em aula que determinam um único triângulo. Se tiver o recurso de projeção, vá para o próximo slide para que os tópicos apareçam. Se não, você pode anotá-los no quadro. Em seguida, peça para que os alunos pensem em siglas que poderiam ser usadas para representar esses três critérios e, depois, vá para o slide 35 para que o segundo balão de fala apareça. Leia o texto com os alunos e verifique se eles têm alguma dúvida sobre o assunto.
É importante que os alunos compreendam que se dois triângulos têm algum desses conjuntos de elementos em comum, então fica garantido que os triângulos são congruentes, ou seja, que possuem lados e ângulos de mesma medida.
Propósito: Relacionar os resultados da investigação feita em aula e o conceito de congruência e critérios de congruência de triângulos .
Sistematização do Conceito

Tempo sugerido: 15 minutos (slides 33 e 35).
Orientações: Leia o primeiro parágrafo do texto e solicite que os alunos digam quais foram os conjuntos de informações vistos em aula que determinam um único triângulo. Se tiver o recurso de projeção, vá para o próximo slide para que os tópicos apareçam. Se não, você pode anotá-los no quadro. Em seguida, peça para que os alunos pensem em siglas que poderiam ser usadas para representar esses três critérios e, depois, vá para o slide 35 para que o segundo balão de fala apareça. Leia o texto com os alunos e verifique se eles têm alguma dúvida sobre o assunto.
É importante que os alunos compreendam que se dois triângulos têm algum desses conjuntos de elementos em comum, então fica garantido que os triângulos são congruentes, ou seja, que possuem lados e ângulos de mesma medida.
Propósito: Relacionar os resultados da investigação feita em aula e o conceito de congruência e critérios de congruência de triângulos .
Encerramento

Tempo sugerido: 10 minutos (slides 36 e 37).
Orientações: Leia o texto e peça para que os alunos façam a tabela em seus cadernos. Dê 5 minutos para que eles realizem a atividade. Em seguida, construa uma tabela no quadro a partir das respostas dos alunos ou exiba a tabela do slide 17. Peça para que os alunos verifiquem se precisam completar algo nas tabelas em seus cadernos.
É importante que os alunos compreendam que os esboços feitos por eles não precisam estar iguais aos da tabela do quadro/projeção, entendendo que são exemplos possíveis.
Propósito: Retomar e sistematizar os critérios de congruência de triângulos.
Encerramento
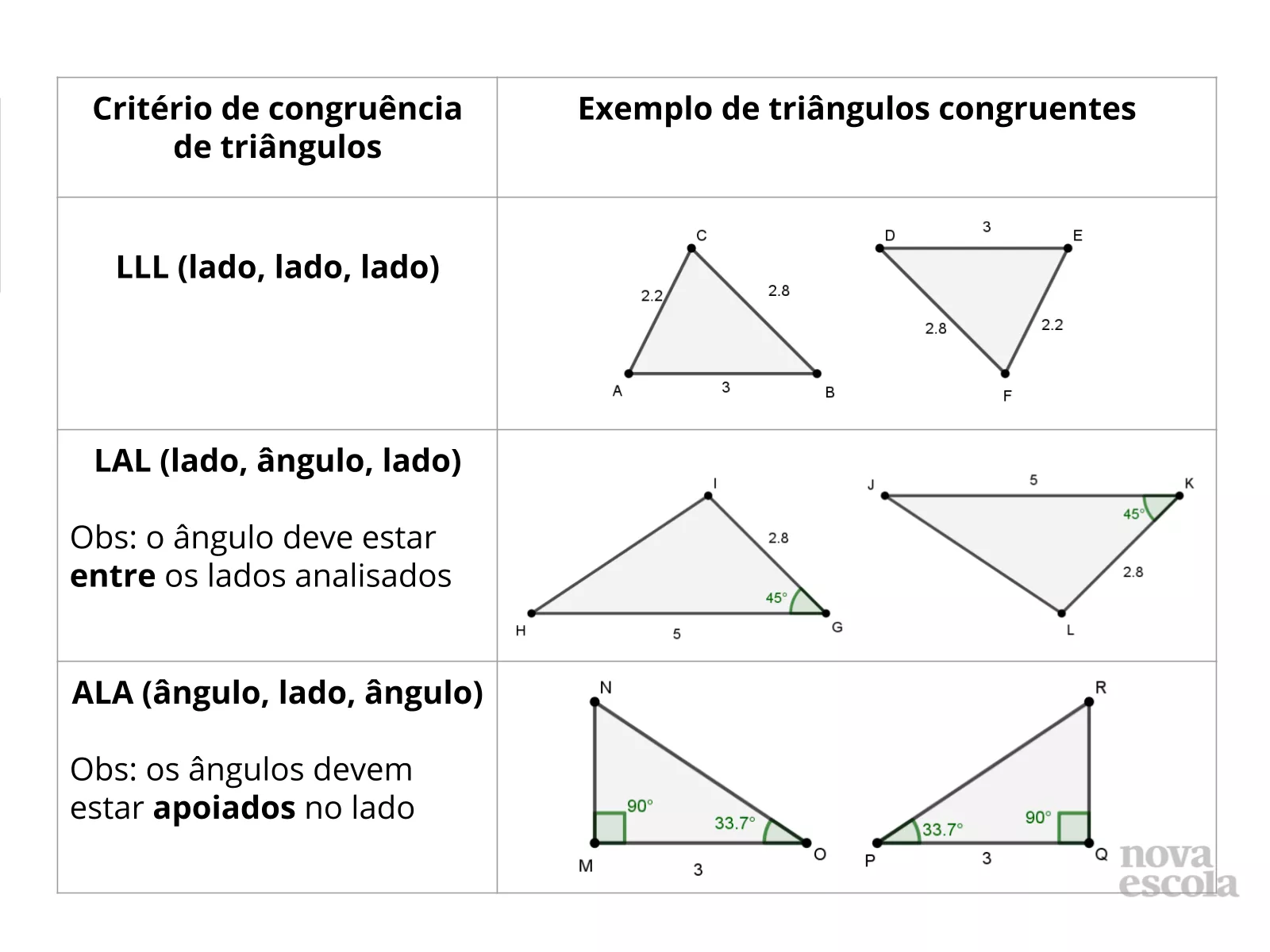
Tempo sugerido: 10 minutos (slides 36 e 37).
Orientações: Leia o texto e peça para que os alunos façam a tabela em seus cadernos. Dê 5 minutos para que eles realizem a atividade. Em seguida, construa uma tabela na lousa a partir das respostas dos alunos ou exiba a tabela do slide 17. Peça para que os alunos verifiquem se precisam completar algo nas tabelas em seus cadernos.
É importante que os alunos compreendam que os esboços feitos por eles não precisam estar iguais aos da tabela da lousa/projeção, entendendo que são exemplos possíveis.
Propósito: Retomar e sistematizar os critérios de congruência de triângulos.

Título: Raio X
Tempo sugerido: 5 minutos.
Orientações: Projete a atividade ou entregue cópias para os alunos e peça que, individualmente, leiam o enunciado e a realizem a atividade. Circule pela classe para verificar como os alunos estão realizando a tarefa e, caso algum aluno termine, solicite que ele construa o triângulo determinado por um dos itens que acredita gerar um único triângulo e duas possibilidades para um item que acredita gerar vários triângulos . O raio X é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. No final, reserve um tempo para um debate coletivo.
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante e avaliar os conhecimentos de cada um a respeito dos critérios de congruência de triângulos aplicados para casos de construção de triângulos.
Utilize o guia de intervenções para analisar dificuldades e realizar intervenções.
Materiais complementares para impressão:
Para os alunos
Para o professor
Sugestão de adaptação para ensino remoto
Código do plano
MAT8_15GEO05
Recursos
USAR APENAS FERRAMENTAS EM PORTUGUÊS E GRATUITAS
- Necessários: Papel, lápis, régua, compasso, transferidor, WhatsApp
- Opcionais: Messenger Sala de aluno ( https://www.messenger.com/groupcall/LINK:4svjhs7dyZw8zoxm/), Meet, Hangout, Zoom, plataforma da Khan Academy ( https://pt.khanacademy.org/)
Portal OBMEP ( https://portaldaobmep.impa.br/index.php/modulo/lista?serie=3)
Geogebra https://play.google.com/store/apps/details?id=org.geogebra&hl=pt_BR
Para este plano, foque na etapa ATIVIDADE PRINCIPAL
Aquecimento
Não é necessário. Pode focar na Atividade principal
Atividade principal
Nessa aula é importante o uso dos materiais indicados para construção dos triângulos. Há várias construções: que envolvem o uso de régua e que envolvem também o uso de transferidor. Você pode selecionar algumas construções ou solicitar a construção de todas. Avalie se sua turma tem habilidade para usar o transferidor e fazer construções considerando determinados ângulos. Caso não tenha, você pode gravar um vídeo orientativo. Você também pode optar pelas construções comente com régua num momento e fazer com transferidos em outro. Encaminhe orientações, via áudio ou vídeo (WhatsApp), focando em informações que permitam que os alunos realizem a atividade autonomamente. Sugerimos que você encaminhe a atividade principal (versão impressa) para os alunos realizarem, solicitando que eles deem um retorno da atividade. Mantenha um canal de comunicação para dúvidas e esclarecimentos.
Na plataforma da Khan Academy há vários vídeos e demais recursos que tratam de construção de triângulos. Você pode selecionar os materiais pertinentes e indicar aos alunos que possuem acesso à internet.
https://pt.khanacademy.org/math/pt-7-ano/geometria-angulos-e-polgonos-7ano/construcao-de-poligonos-regulares/v/construo-de-tringulo -
https://pt.khanacademy.org/math/basic-geo/basic-geometry-shapes/basic-geo-classifying-triangles/v/constructing-triangles-with-constraints
No Portal da OBMEP há exploração dos elementos básicos da geometria plana (partes 1, 2 e 3) que pode servir de apoio aos alunos que possuem internet.
https://portaldaobmep.impa.br/index.php/modulo/lista?serie=3
Discussão das soluções
Avalie as respostas e dúvidas apresentadas pelos alunos para dar um feedback à turma. Use informações da Sistematização do conceito para compor seu feedback. Grave um áudio ou vídeo curto (WhatsApp) para dar um ‘fechamento’ à aula. Você pode fazer um registro escrito com as principais informações e conceitos da aula para os alunos copiarem ou imprimirem. Provavelmente você terá que retomar essa aula com as atividades do Raio x e também das atividades complementares. Se sua turma dispuser de ferramentas e internet, dê preferência por realizar as discussões em tempo real, por meio de uma das plataformas sugeridas abaixo. Mas, não esqueça de manter um canal de comunicação para discussão também dessas novas atividades.
Se for possível discutir em tempo real com sua turma, use o Meet, Hangout ou Zoom e considere apenas os itens e os conceitos de maior relevância.
Você pode usar também o Messenger Sala de aluno https://www.messenger.com/groupcall/LINK:4svjhs7dyZw8zoxm/
Sistematização
Use nas discussões
Encerramento
Use nas discussões
Raio X
Use o Raio X e as atividades complementares como forma de revisão para consolidação das aprendizagens. Não esqueça de retomar discussões também dessas atividades e focar nos pontos de aprendizagem mais críticos. Provavelmente, será necessário cumprir com essas atividades os passos realizados na Atividade principal.
Convite às famílias
Pode ser proposta algumas construções com uso de régua, por exemplo.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Renata Akemi Maekawa
Mentor: Fabricio Eduardo Ferreira
Especialista de área: Pricilla Cerqueira
Habilidade da BNCC
EF08MA12 - Demonstrar propriedades de quadriláteros por meio da identificação da congruência de triângulos.
Objetivos específicos
- Construir triângulos a partir de informações utilizando instrumentos geométricos.
- Analisar a quantidade de possibilidades de construções para cada conjunto de informações fornecidos.
- Elaborar critérios de congruência de triângulos.
- Compreender o conceito de congruência de triângulos
Conceito-chave
Critérios de congruência de triângulos
Recursos necessários
Régua, compasso, transferidor, folhas de sulfite e fichas impressas.
Projetor (se possível)















