Sugestão de adaptação para ensino remoto
Código do plano
MAT6_15GEO09
Recursos
- Necessários: Folha sulfite, lápis, caderno , barbante ou linhas coloridas (costura, lã), transferidor, régua, cola
- Opcionais: Meet, Zoom, WhatsApp, Paint
Como classificar quadriláteros: https://pt.khanacademy.org/math/basic-geo/basic-geometry-shapes/basic-geo-quadrilaterals/v/classifying-shapes
Introdução à quadriláteros: https://pt.khanacademy.org/math/basic-geo/basic-geometry-shapes/basic-geo-quadrilaterals/v/quadrilateral-overview
Para este plano, foque na etapa: Atividade Principal
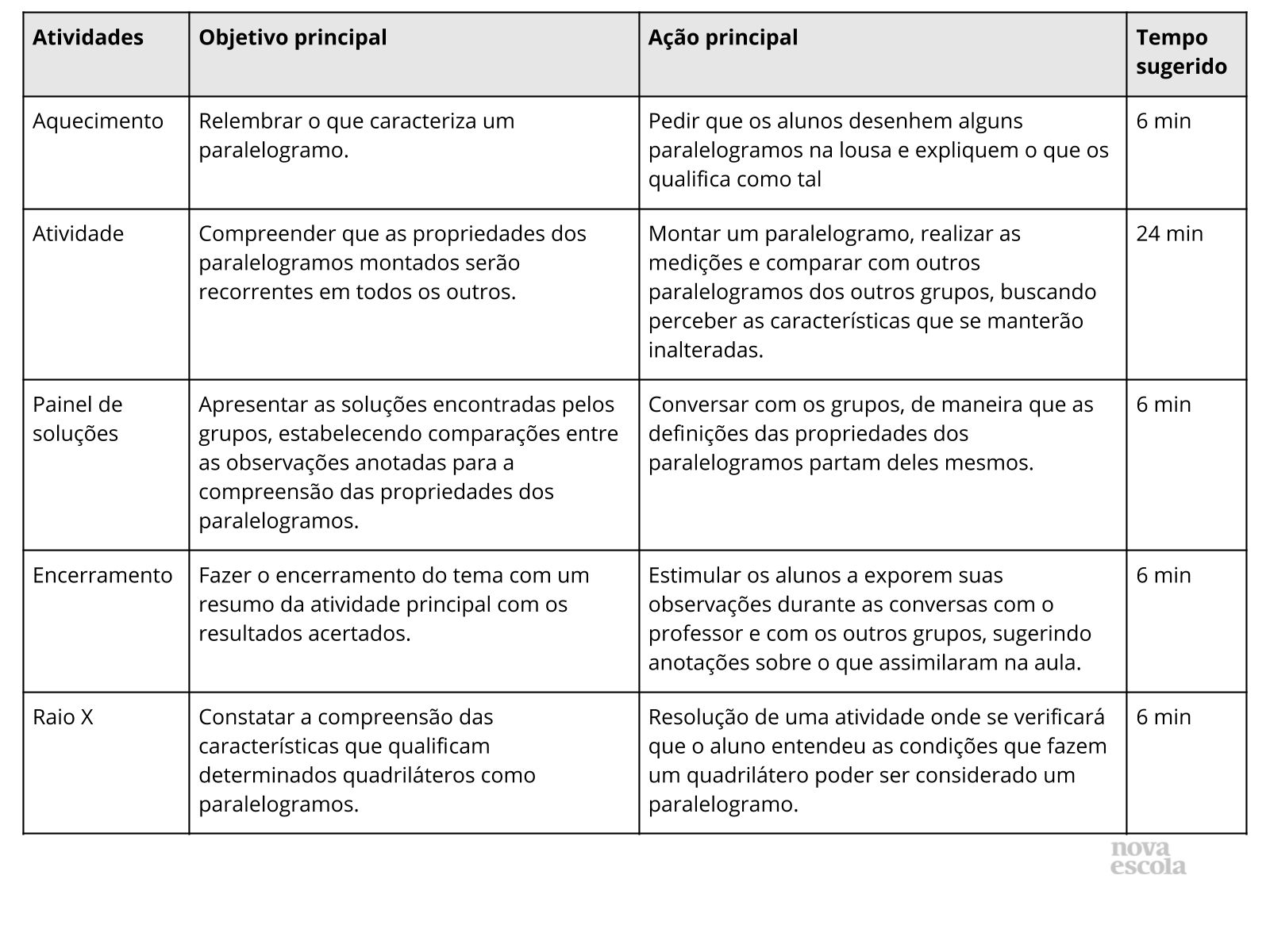
Aquecimento
O aquecimento pode ser usado de forma síncrona com os alunos. Desenhe em tempo real, utilizando o Paint (ou outra ferramenta), alguns paralelogramos e pergunte algumas características sobre eles. Faça as perguntas do slide do próprio Aquecimento. Caso o aluno não possua internet, envie pelo WhatsApp as figuras e as respostas podem ser apresentadas por escrito e enviadas ao professor.
Atividade Principal
Você pode fazer uma sala de aula invertida. Nessa aula é importante o uso da régua e transferidor para a construção dos paralelogramos. Avalie se sua turma tem habilidade para usar o transferidor e fazer essas análises de diagonais e ângulos. Caso não tenha, você pode gravar um vídeo orientativo. Mantenha um canal de comunicação para dúvidas e esclarecimentos antes do encontro combinado. É importante que eles tenham feito a atividade antes do encontro, mesmo com dúvidas. No dia do encontro marcado (Meet, Hangouts, Zoom, Teams), deixe que os alunos compartilhem suas observações. Construa os paralelogramos com as medidas propostas na atividade, trace as diagonais e os ângulos. Compartilhe a tela para que eles possam analisar. Faça as perguntas que estão no slide da “Atividade Principal” para que percebam por eles mesmos as propriedades dos paralelogramos com relação a seus ângulos e diagonais. Se sua aula fora assíncrona, deixe a tarefa na escola ou envie pelo WhatsApp. Grave um áudio explicando e peçam que enviem para você combinando um retorno de devolutiva. Nesse retorno, você pode enviar o print com registros dos outros alunos para que eles comparem com suas estratégias e colem no seu caderno como repertório de soluções.
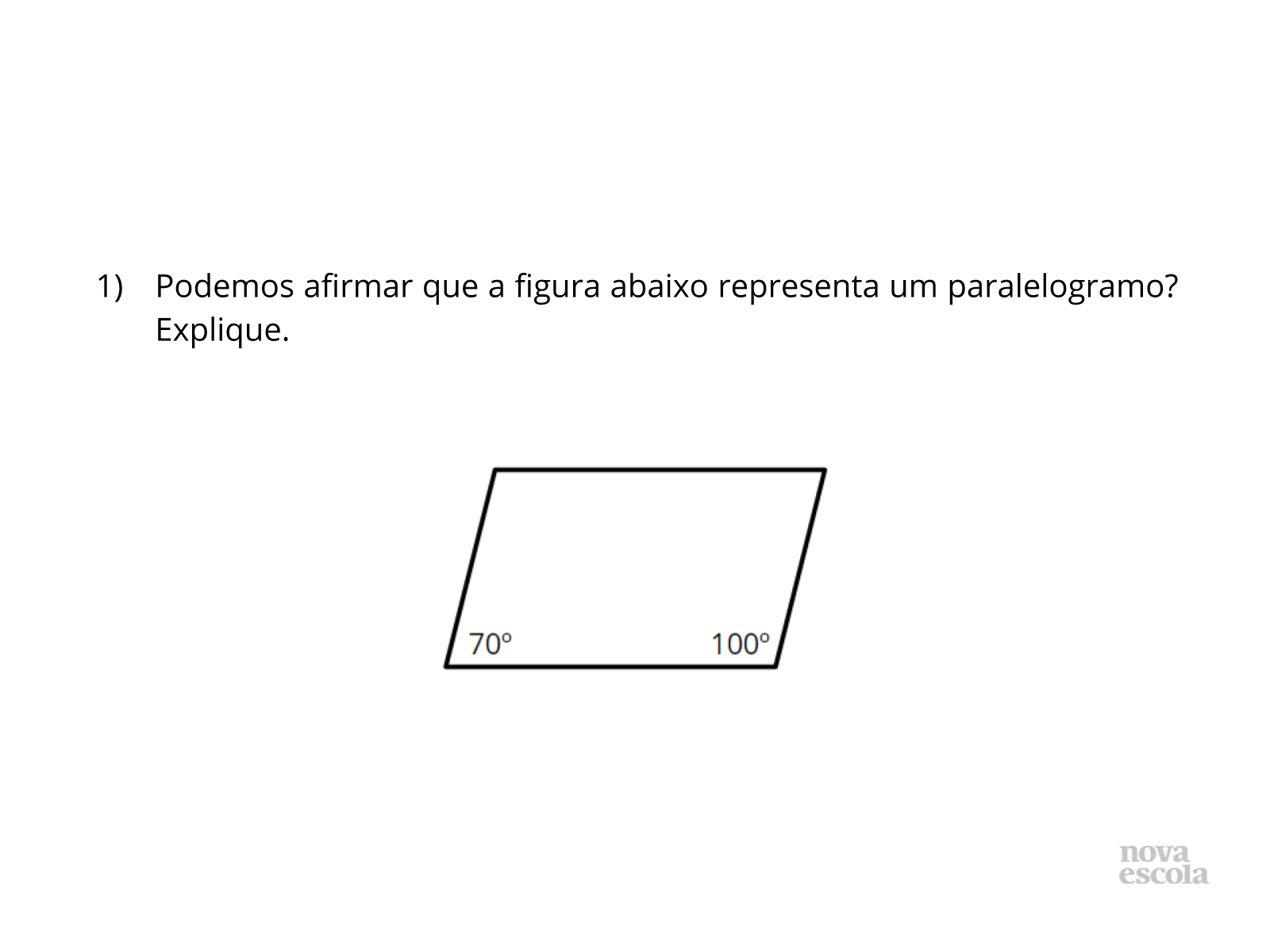
Raio X
Use o Raio X e as atividades complementares como forma de revisão para consolidação das aprendizagens. Não esqueça de retomar discussões também dessas atividades e focar nos pontos de aprendizagem mais críticos.
Convite às famílias
A participação das famílias no processo de aprendizagem é de grande importância para o aluno. Porém, ressaltamos que os pais não são professores de matemática e muitos estão ocupados com outras funções em casa. Portanto, indicamos a participação das famílias no compartilhamento e discussão de possíveis soluções para os problemas propostos.