Código do plano: MAT6_03NUM08
Recursos
- Necessários: Caderno, lápis, borracha, régua, uma folha com malha quadriculada, grupo de WhatsApp
- Opcionais: lápis de cor ou giz de cera
Para este plano, foque na etapa: Atividade Principal e Raio X
Atividade Principal
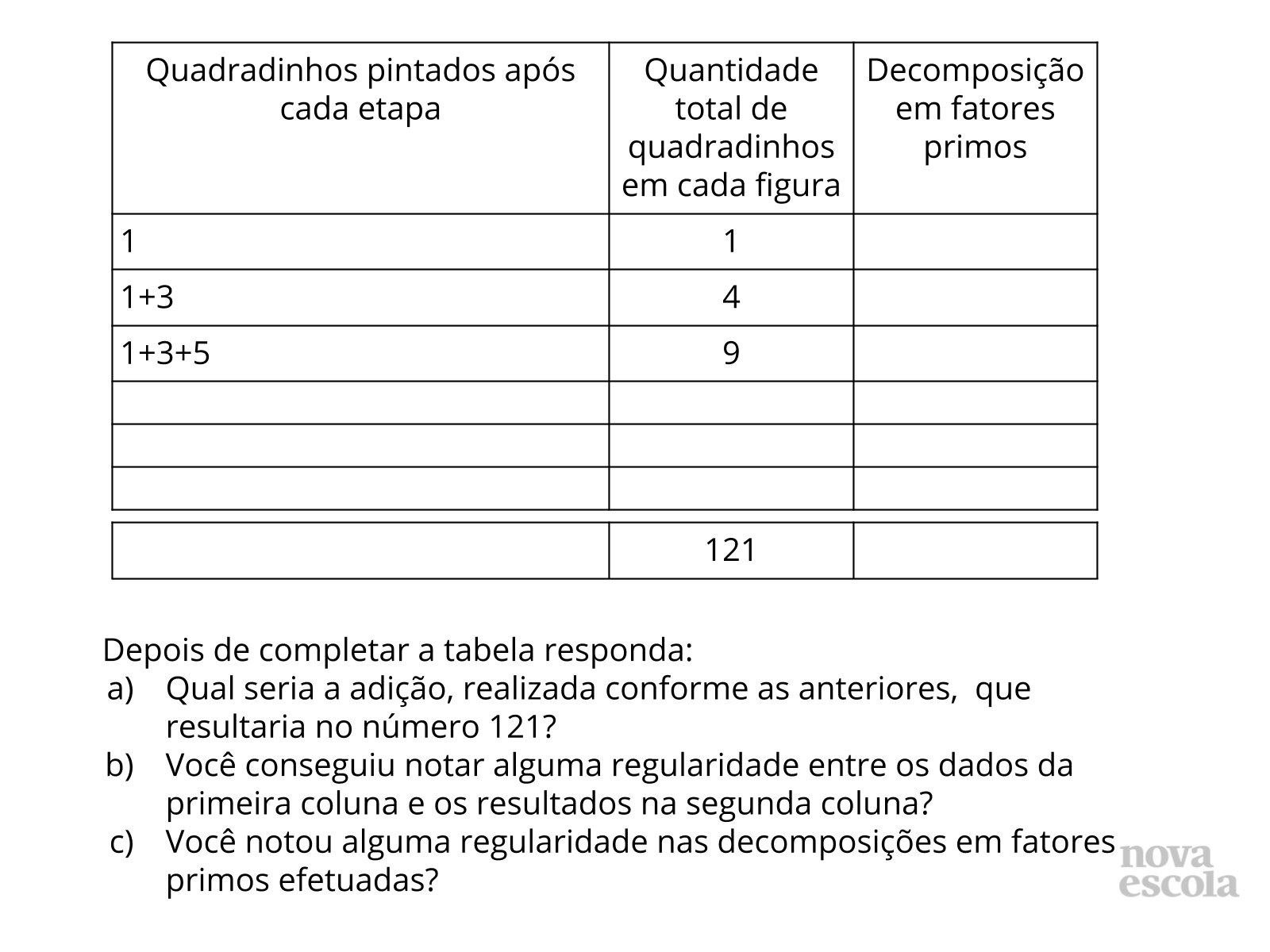
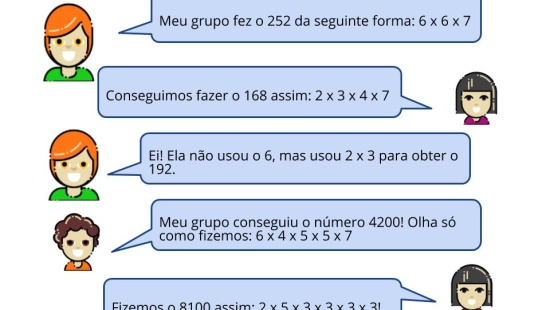
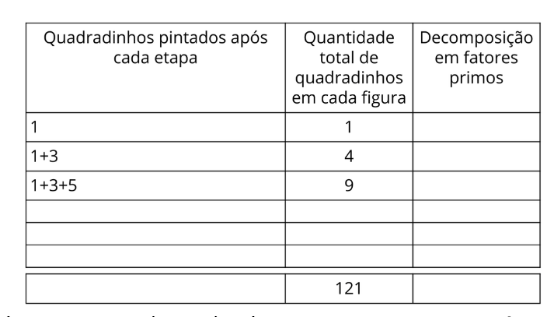
Professor, inicie essa aula compartilhando com os alunos o slide da Atividade Principal. Oriente-os a fazer a leitura da situação proposta e peça que reproduzam os quadradinhos na malha quadriculada, a cada etapa pintando com cores diferentes. Caso algum aluno não tenha lápis de cor, pode usar símbolos para diferenciar cada etapa. Em seguida peça que organizem uma tabela no caderno, conforme as orientações no slide. Oriente-os a preencher a tabela de acordo com o que observaram na malha quadriculada. Fique atento, pois é possível que alguns alunos apresentem dificuldades e precisem de orientações mais específicas tanto na confecção dos quadrados quanto no preenchimento da tabela. Você pode compartilhar com eles a imagem da tabela pronta que está no slide 2 da Atividade principal. Dê um tempo para que eles realizem a proposta e em seguida peça a eles que fotografem suas malhas e tabelas em uma única imagem e compartilhem no grupo.
Discussão das soluções
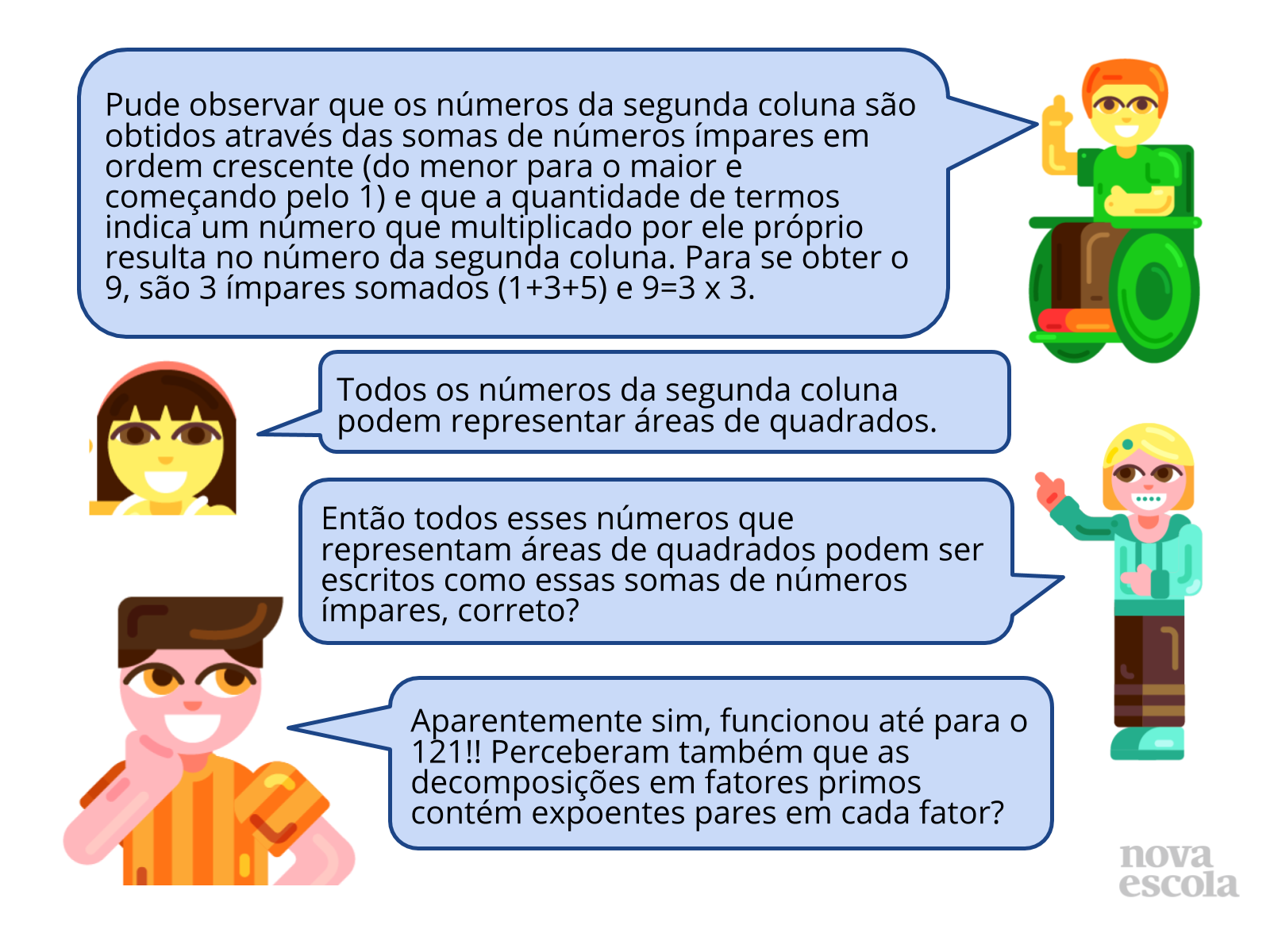
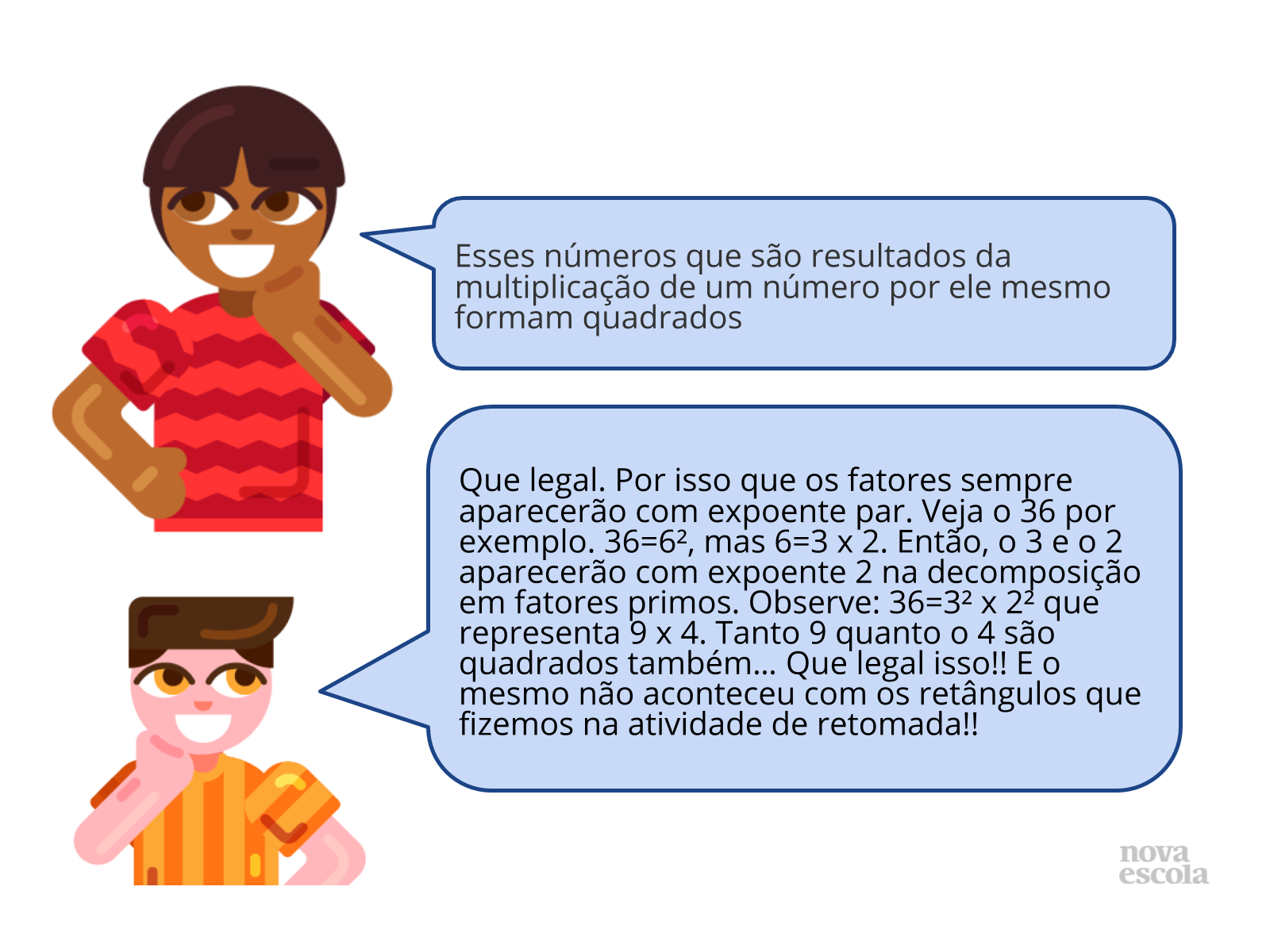
Essa é uma etapa importantíssima da aula, pois nela os alunos irão justificar as estratégias e respostas usadas para a resolução do problema proposto na atividade principal. Estimule os alunos a analisar e comparar as imagens compartilhadas pelos colegas. Peça que acionem seus microfones e expliquem como pensaram para atender o que foi solicitado. Faça com que percebam a importância de seguir os comandos com atenção. Lembre-se que o objetivo da aula é que os alunos reconheçam um número quadrado perfeito a partir de sua decomposição em fatores primos. Sendo assim, explore essa atividade, em especial a organização dos dados na tabela para que eles possam perceber as regularidades nessa construção. Para isso, invista em boas perguntas: “Por que há sempre um número ímpar de quadradinhos a serem pintados cada vez que é preciso fazer um novo quadrado?”, “Como vocês escreveram o quadradinho 1 em fatores primos?”, “O que vocês observaram nos fatores primos de cada número?". A partir dessas perguntas, encaminhe a aula para o encerramento, garantindo que eles estabeleçam relações entre os quadrados e a quantidade de fatores primos. Finalize sistematizando que por terem essas características, esses números são conhecidos como “quadrados perfeitos”.
Raio X
Proponha as atividades do Raio X como tarefa de casa e combine um momento para você dar a devolutiva dessa tarefa. Você pode gravar um áudio ou um podcast explicando se cada número é um quadrado perfeito ou não, reforçando a característica dos números quadrados perfeitos de terem apenas dois fatores primos iguais.
Convite às famílias
A participação das famílias no processo de aprendizagem é de grande importância para o aluno. Porém, ressaltamos que os pais não são professores de matemática e muitos podem estar ocupados com outras funções em casa ou mesmo trabalhando. Portanto, indicamos a participação das famílias no compartilhamento e discussão de possíveis soluções para os problemas propostos ou interagindo com o aluno em alguma atividade específica. Compartilhe com os alunos o link do vídeo “Como saber se um número é quadrado perfeito?” (https://www.youtube.com/watch?v=uXMIj8rFe2A) e sugira aos alunos que assistam com seus familiares.
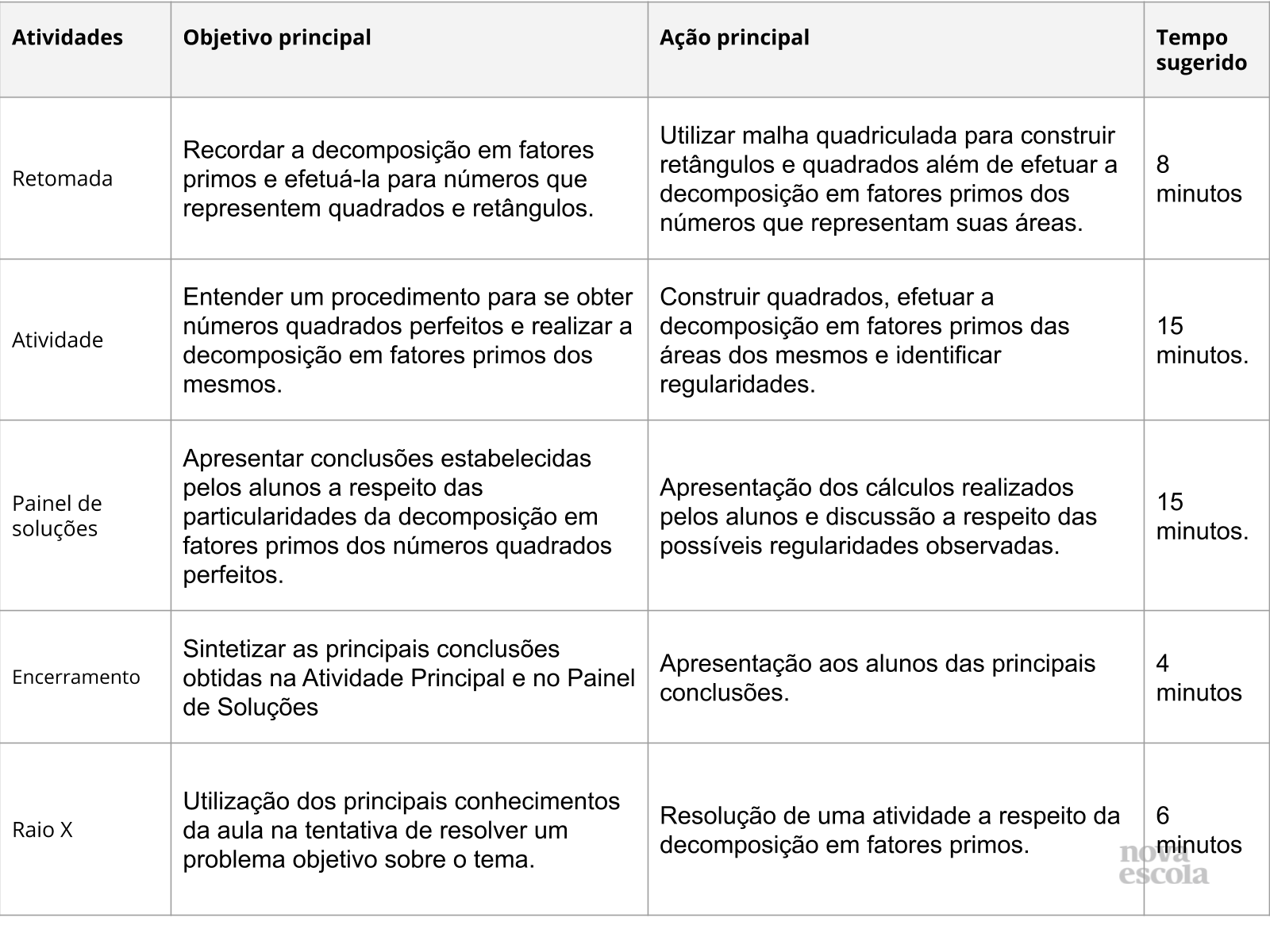 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.