Resumo da aula
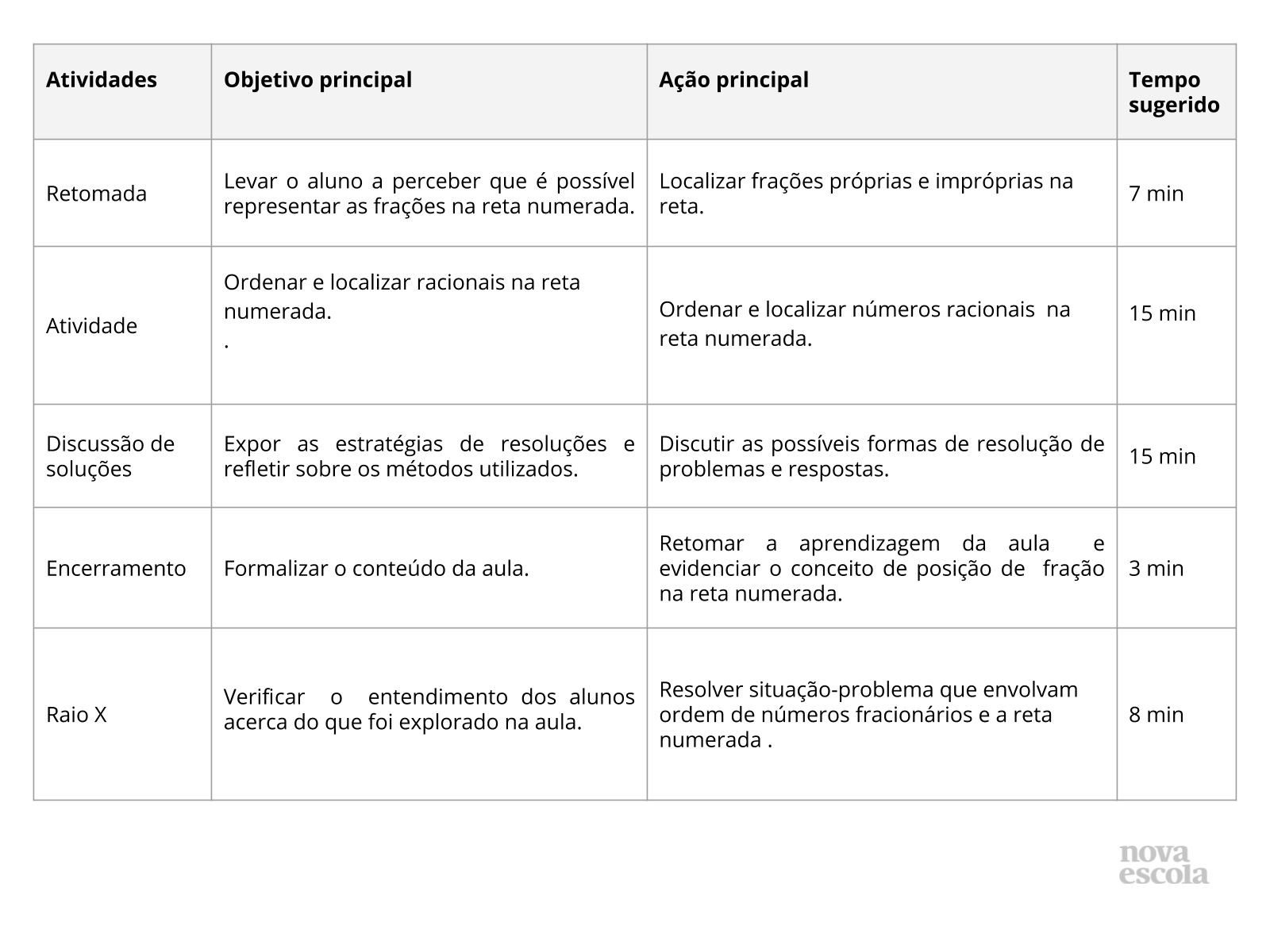
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada
Tempo sugerido: 7 minutos.
Orientações: Inicie a aula propondo aos alunos a construção de uma reta numerada. Peça a um aluno que venha ao quadro e marque o número natural zero. Ao conduzir esta aula aproveite para relembrar alguns conceitos como sucessor, antecessor. Continue montando a reta até o número 3. Ressalte aos alunos a importância de, ao construir a reta, manter a mesma distância entre os números naturais, pois este fato será importante quando os alunos forem representar as frações na reta.
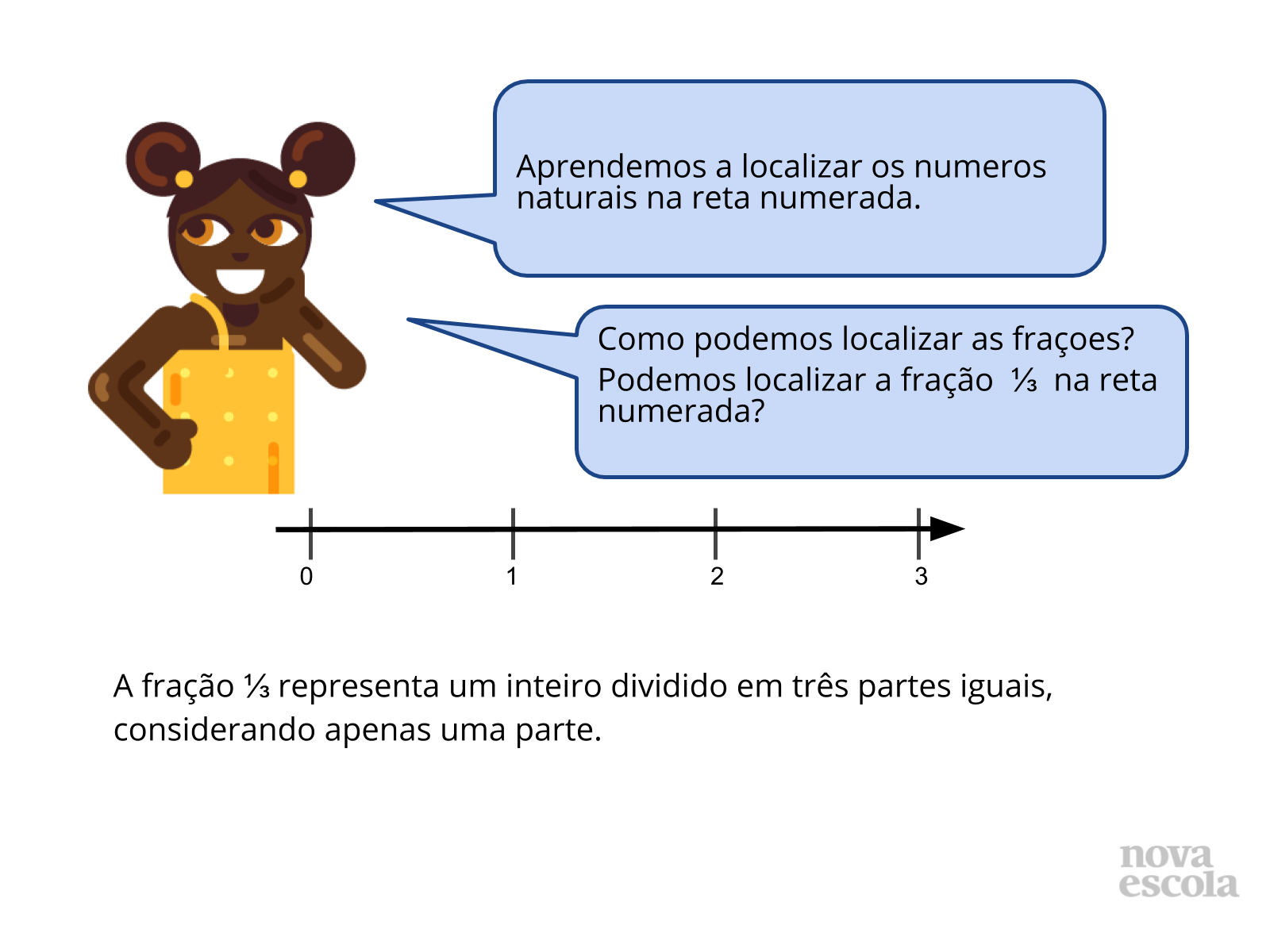
Em seguida, questione os alunos sobre como é possível localizar frações na reta numerada. Peça a um aluno que venha ao quadro e marque como ele faria a localização da fração.
Propósito: Fazer vir à tona, pela voz dos alunos, os conceitos que eles já possuem sobre reta numerada de números naturais e introduzir algumas frações na reta .
Discuta com a turma:
- Onde o zero deve estar? No meio? Na ponta da esquerda da reta?
- Quem é o sucessor do 0?
- Qual o antecessor do 2?
- Existe algum numero entre o 0 e 1?
- A fração que você marcou é menor ou maior do que 1?
Retomada
Tempo sugerido: 7 minutos.
Orientações: Inicie a aula propondo aos alunos a construção de uma reta numerada. Peça a um aluno que venha ao quadro e marque o número natural zero. Ao conduzir esta aula aproveite para relembrar alguns conceitos como sucessor, antecessor. Continue montando a reta até o número 3. Ressalte aos alunos a importância de, ao construir a reta, manter a mesma distância entre os números naturais, pois este fato será importante quando os alunos forem representar as frações na reta.
Em seguida, questione os alunos sobre como é possível localizar frações na reta numerada. Peça a um aluno que venha ao quadro e marque como ele faria a localização da fração.
Propósito: Fazer vir à tona, pela voz dos alunos, os conceitos que eles já possuem sobre reta numerada de números naturais e introduzir algumas frações na reta .
Discuta com a turma:
- Onde o zero deve estar? No meio? Na ponta da esquerda da reta?
- Quem é o sucessor do 0?
- Qual o antecessor do 2?
- Existe algum numero entre o 0 e 1?
- A fração que você marcou é menor ou maior do que 1?
Atividade principal
Tempo sugerido: 15 minutos.
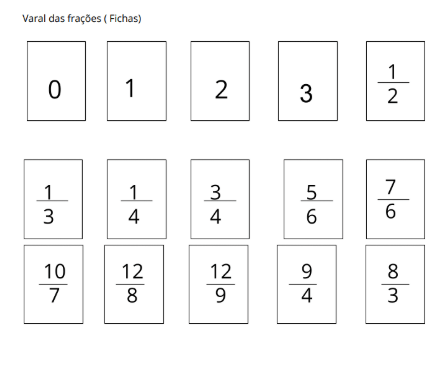
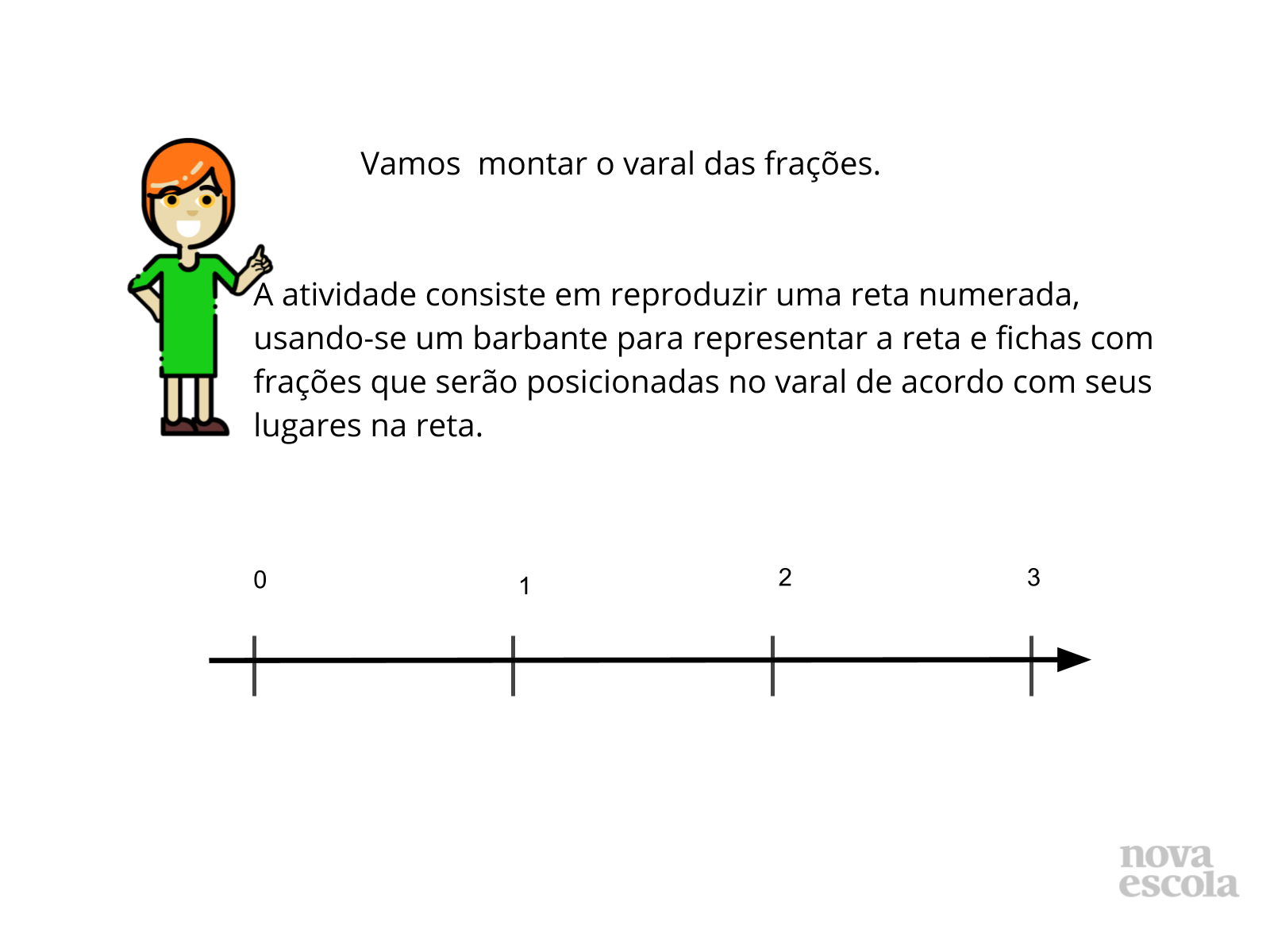
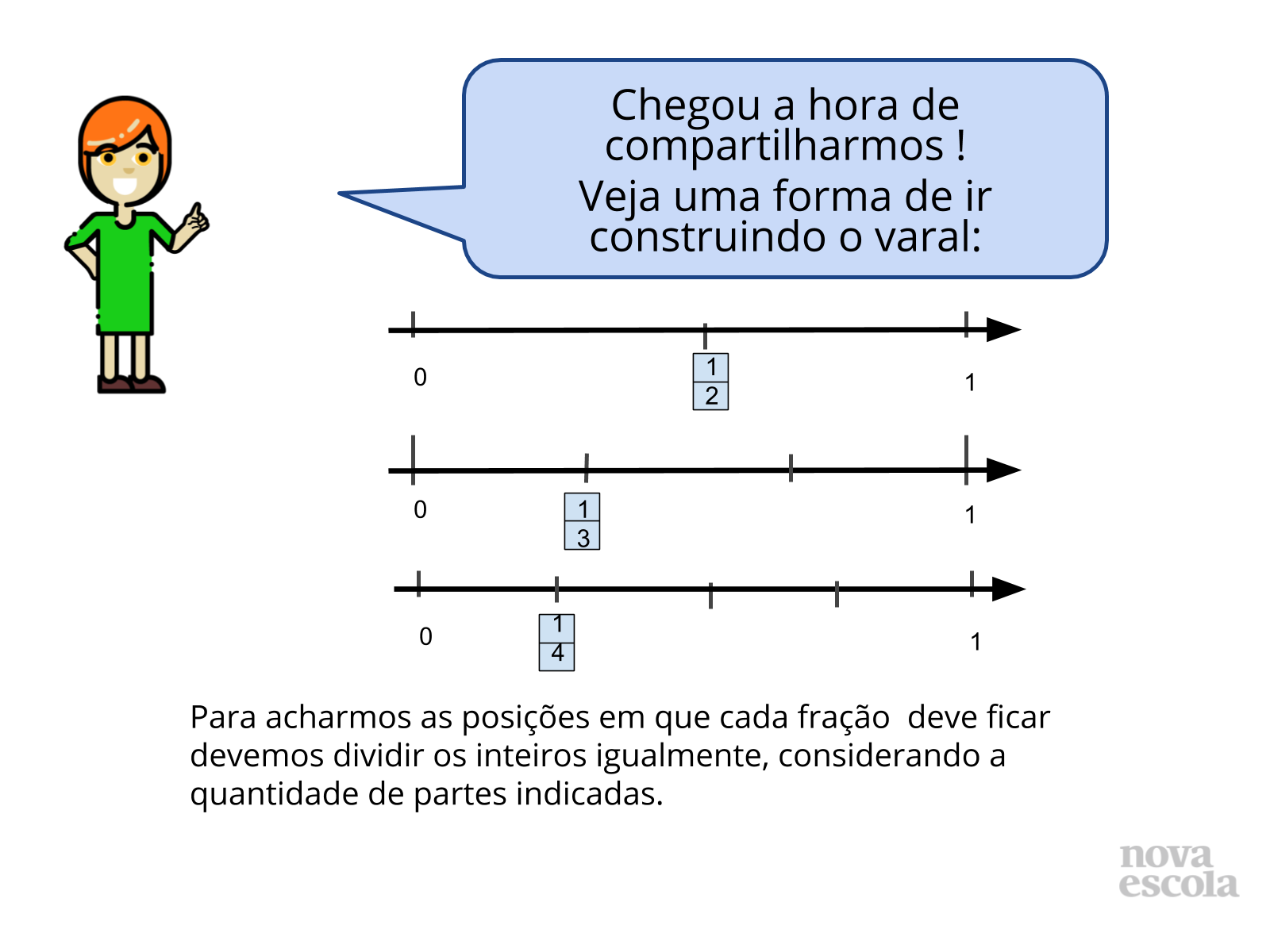
Orientação: Divida a turma em grupos. Você poderá escrever o enunciado da atividade no quadro, projetá-lo ou entregar uma cópia aos alunos. Peça aos estudantes para que leiam as instruções da atividade a ser desenvolvida e se organizem em grupos de 4 a 5 alunos. Entregue um pedaço de barbante e um conjunto de fichas com frações (ver materiais complementares) a cada grupo e deixe bem claro que cada grupo deverá construir seu próprio varal das frações. Dê tempo para que tentem resolver, deixe que discutam entre eles sobre a localização das frações na reta. Não faça nenhuma intervenção neste momento, observe como eles organizam e quais as estratégias que eles utilizam.
Propósito: Ordenar e localizar as fraçoes na reta numerada.
Materiais complementares:
Atividade principal
Resolução do atividade principal
Guia de intervenção
Painel de soluções
Tempo sugerido: 15 minutos.
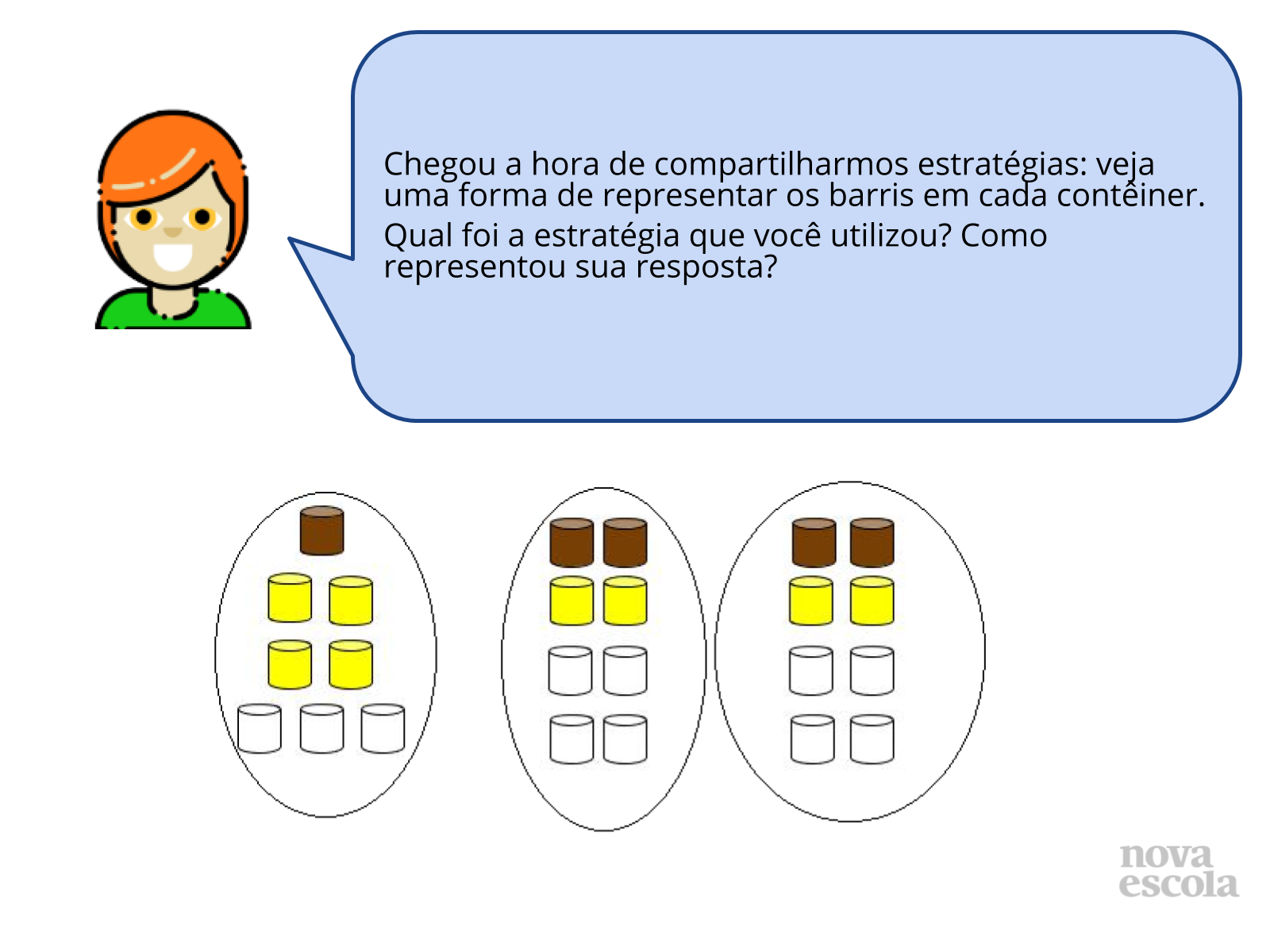
Orientações: Peça aos alunos que compartilhem as estratégias que usaram, peça para que registrem na lousa .
Propósito: Realizar um fechamento das ideias discutidas até o momento. Comparar as respostas dos grupos.
Discuta com a turma:
- Alguém chegou em uma solução diferente dessa? Você poderia explicar como fez?
- Qual caminho você utilizou para concluir esta localização da fração?
- Existe outra maneira de determinar a localização desta fração na reta numerada?
Encerramento

Tempo sugerido: 3 minutos.
Orientação: Concluir e retomar a ideia central da aula. Verifique se algum aluno possui dúvidas sobre o que aprenderam.
Propósito: Retomar a aprendizagem da aula e evidenciar a localização de frações na reta numerada.
Raio x
Tempo sugerido: 8 minutos.
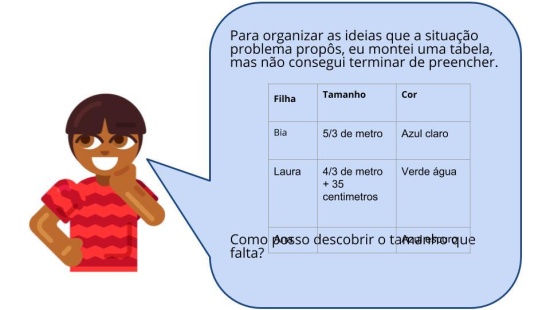
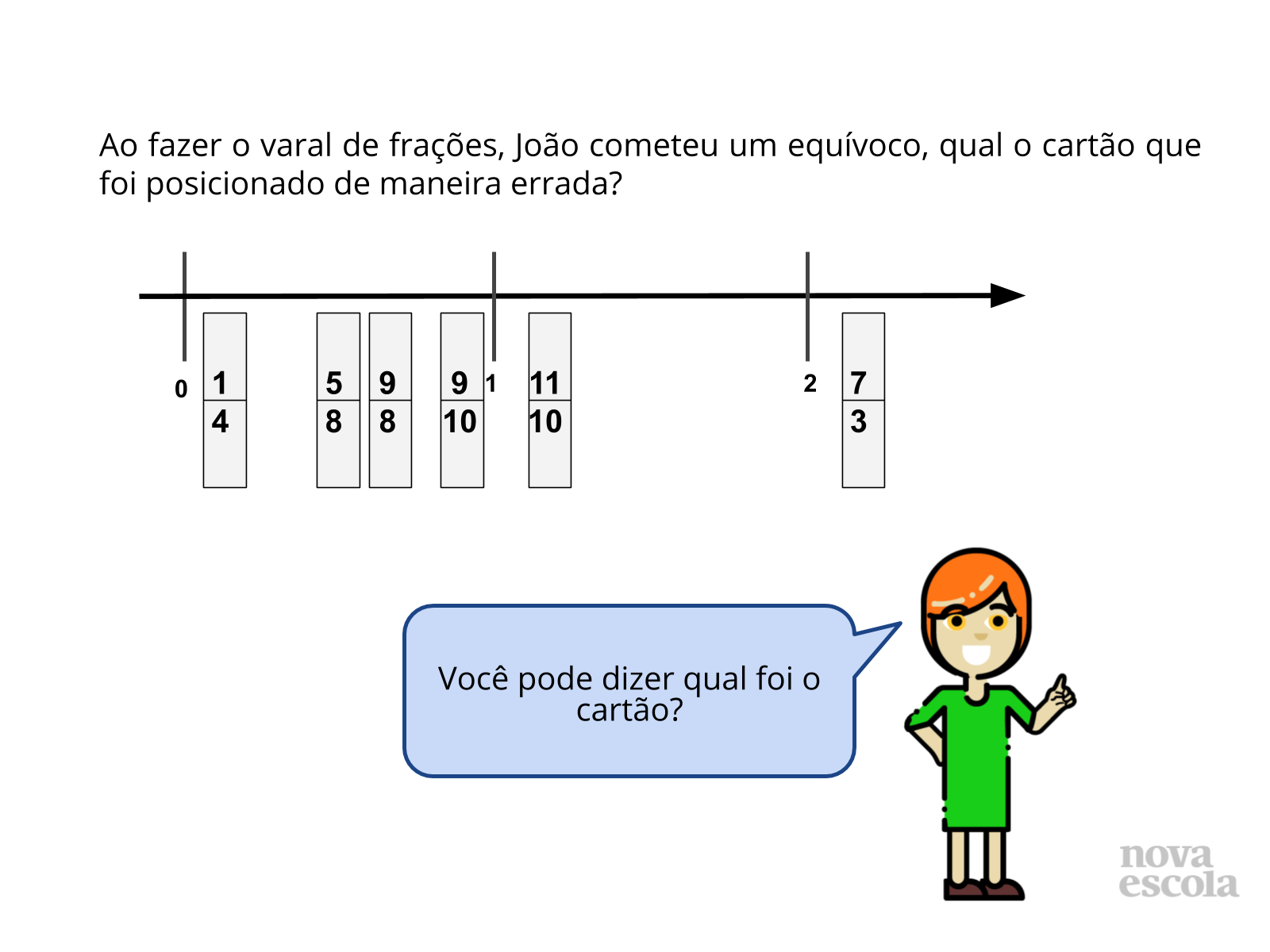
Orientações: Apresente a nova situação e peça que os estudantes leiam o problema e resolvam. O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. Após apresentar a nova situação, circule pela sala, para verificar como estão montando as representações. Você pode projetar, passar no quadro ou fazer cópia para os alunos. No final, reserve um tempo para um debate coletivo registrando as soluções na lousa.
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante e avaliar os conhecimentos de cada um a respeito da localização de fração na reta numerada.
Discuta com a turma:
- Como você fez para representar o problema?
- Você entendeu o que o problema propos?
- Como fez para identificar o cartão em posição errada?
- Como chegou a resposta?
Materiais complementares:
Raio x
Resolução do raio x
Atividade complementar
Resolução do atividade complementar