Objetivo
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Samara Cintia Pinho de Moraes
Mentor: Fabio Menezes da Silva
Especialista de área: Fernando Barnabé
Habilidade da BNCC
EF05MA20) Concluir, por meio de investigações, que figuras de perímetros iguais podem ter áreas diferentes e que, também, figuras que têm a mesma área podem ter perímetros diferentes.
Objetivos específicos
- Reconhecer que polígonos podem ter o mesmo perímetro e áreas diferentes.
Conceito-chave
Perímetro e área de figuras planas.
Recursos necessários
Caderno, lápis,borracha, papel quadriculado, lápis de cor e papel sulfite para fotocópias.
Tempo sugerido: 2 minutos
Orientação: Fazer leitura compartilhada com os alunos
Discuta com a turma:
- Vocês podem me dizer o que é perímetro e área?
- Qual a diferença entre os dois?
Retomada
Tempo sugerido: 10 minutos
Orientação: A noção de perímetro e área são relembrados por meio de perguntas conceituais e reforçando com uma atividade simples.
Propósito: Relembrar o conceito de perímetro e área de uma figura.
Discuta com a turma:
- Quem pode me dizer o que lembra sobre perímetro?
- E área?
- Como fazemos para achar a medida das duas?
Retomada
Tempo sugerido: 10 minutos
Orientação: A noção de perímetro e área são relembrados por meio de perguntas conceituais e reforçando com uma atividade simples.
Propósito: Relembrar o conceito de perímetro e área de uma figura.
Discuta com a turma:
- Quem pode me dizer o que lembra sobre perímetro?
- E área?
- Como fazemos para achar a medida das duas?
Atividade Principal
Tempo sugerido: 15 minutos
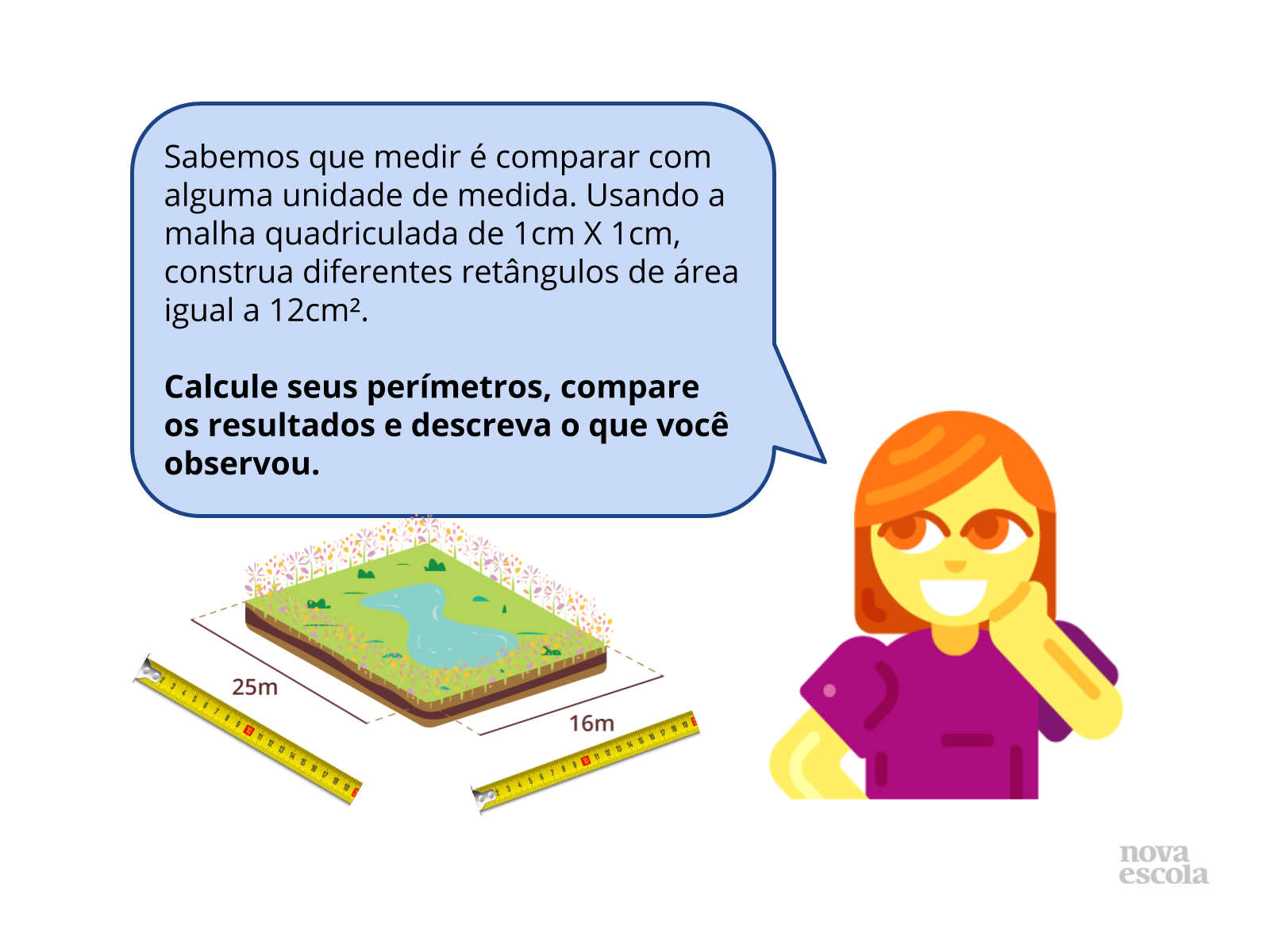
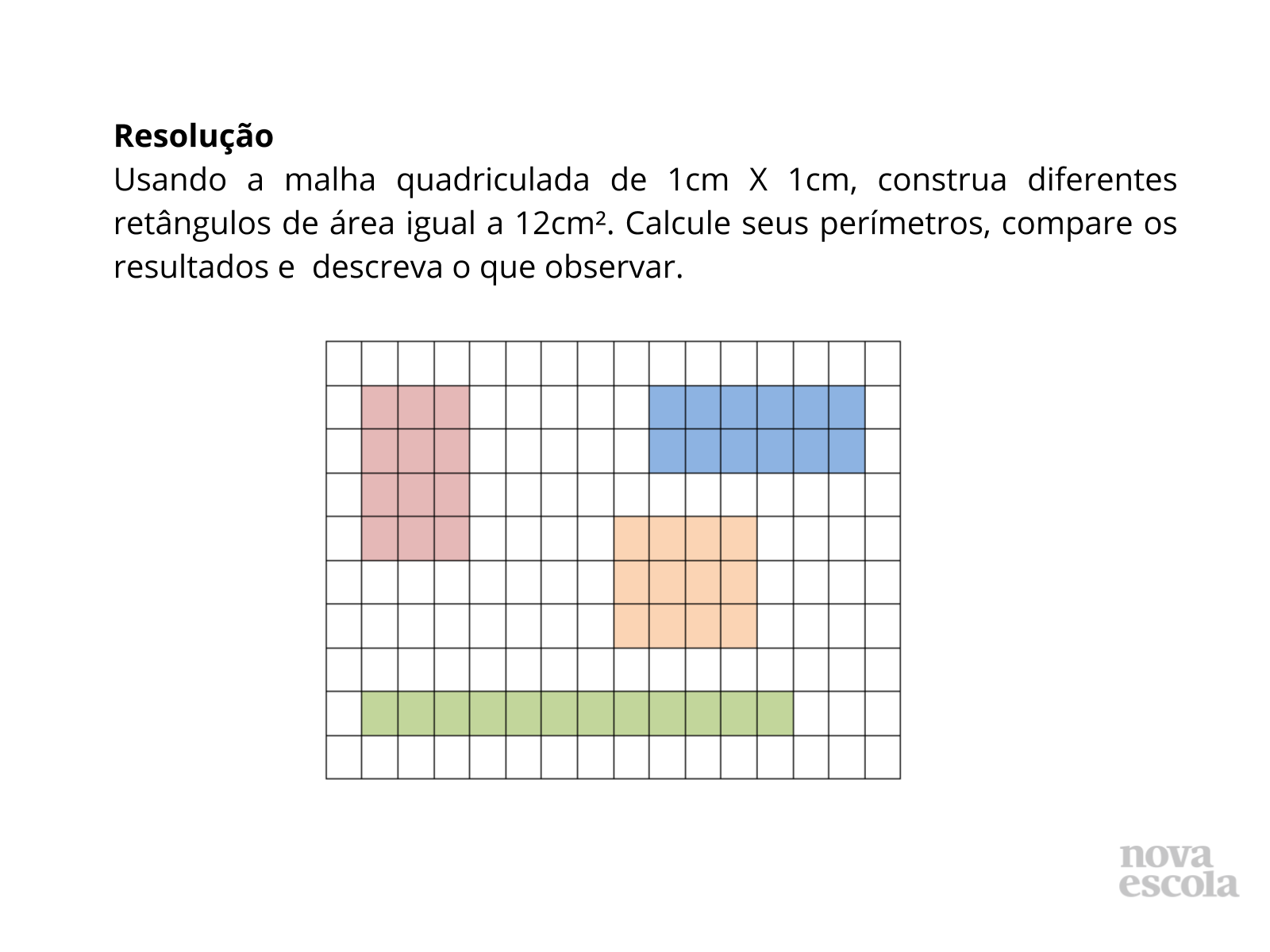
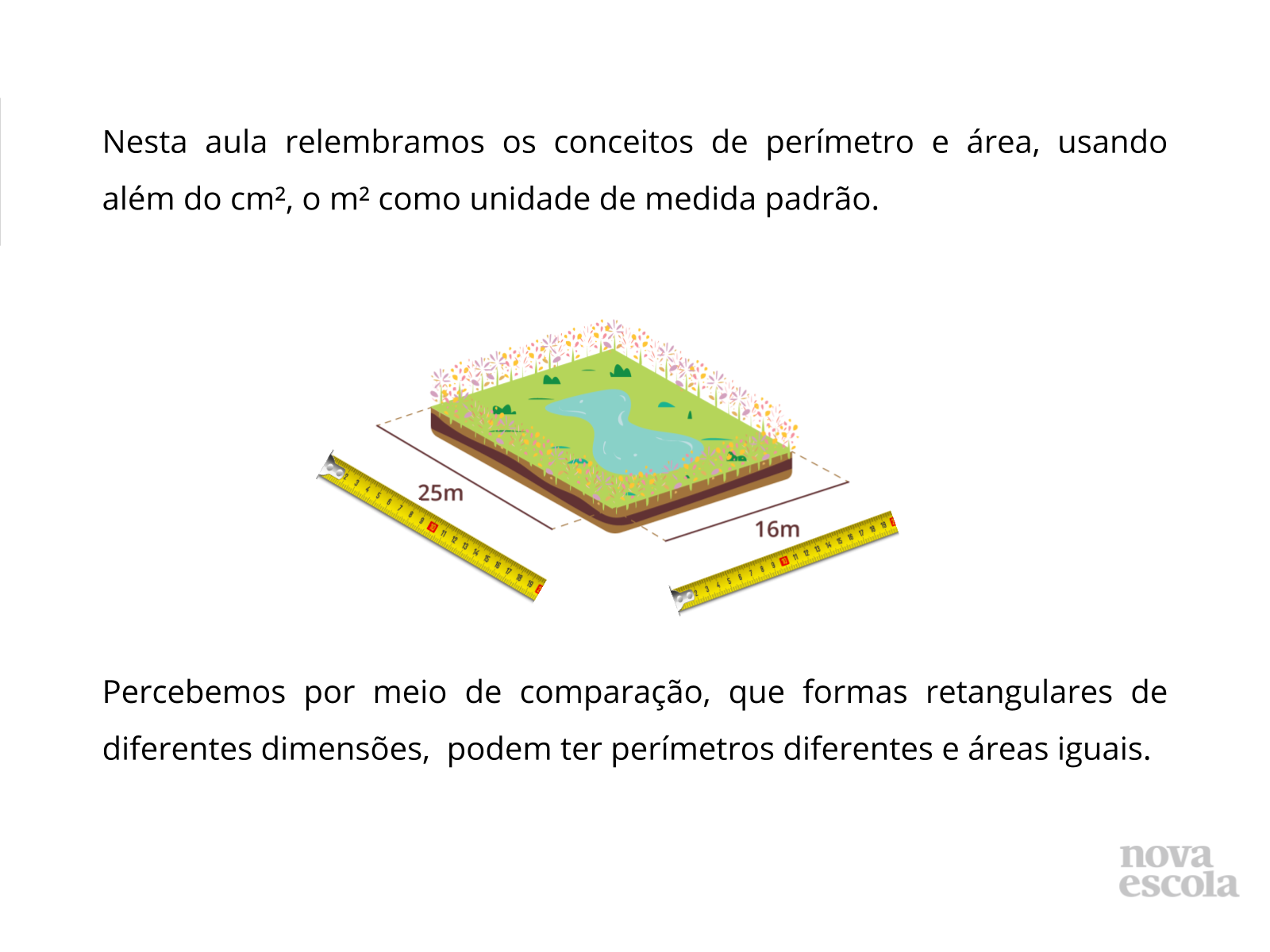
Orientação: Os alunos devem ser separados em grupos de 4. O enunciado do problema pode ser passado na lousa ou dado em folha fotocopiada para os grupos. Inicialmente, deve-se ler o enunciado do problema para classe e esclarecendo que o mesmo tem que ser resolvido em duas etapas. Ná primeira parte, deverão desenhar os retângulos possíveis a serem criados e que tenham área igual a 12cm². Na segunda parte, deverão calcular os perímetros de todos eles e fazer a comparação, verificando então, que as figuras possuem a mesma área, mas não o mesmo perímetro. Discuta a importância de se ter unidade padrão, quais são eles e porque temos submúltiplos dessas unidades (nesse caso, para melhor medir pedaços e comprimentos menores que a unidade padrão, assim como fazemos com outras unidades como a monetária por exemplo, fazemos com todas).
Propósito: Cálculo de perímetro e área de uma região retangular, usando como medida padrão o m².
Discuta com a turma:
- Para resolver esse problema o que é preciso fazer primeiro?
- Vocês calcularam os perímetros e o quê puderam perceber?
Atividade Principal
Tempo sugerido: 15 minutos
Orientação: Os alunos devem ser separados em grupos de 4. O enunciado do problema pode ser passado na lousa ou dado em folha fotocopiada para os grupos. Inicialmente, deve-se ler o enunciado do problema para classe e esclarecendo que o mesmo tem que ser resolvido em duas etapas. Ná primeira parte, deverão desenhar os retângulos possíveis a serem criados e que tenham área igual a 12cm². Na segunda parte, deverão calcular os perímetros de todos eles e fazer a comparação, verificando então, que as figuras possuem a mesma área, mas não o mesmo perímetro. Discuta a importância de se ter unidade padrão, quais são eles e porque temos submúltiplos dessas unidades (nesse caso, para melhor medir pedaços e comprimentos menores que a unidade padrão, assim como fazemos com outras unidades como a monetária por exemplo, fazemos com todas).
Propósito: Cálculo de perímetro e área de uma região retangular, usando como medida padrão o m².
Discuta com a turma:
- Para resolver esse problema o que é preciso fazer primeiro?
- Vocês calcularam os perímetros e o quê puderam perceber?
Materiais complementares para impressão:
Discussão da solução
Tempo sugerido: 10 minutos
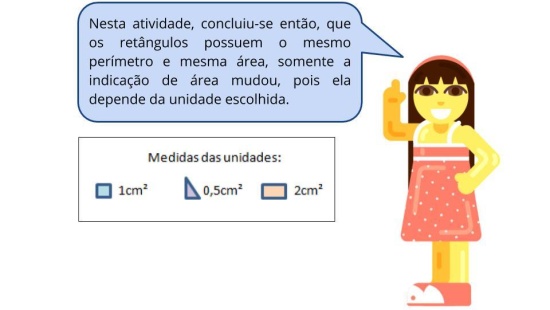
Orientações: O professor será o direcionador das discussões em sala. Os resultados e soluções serão organizados, sistematizados e resumidos os resultados e resoluções encontradas pelos alunos. Nesse momento da aula, é importante promover a socialização das estratégias usadas pelos alunos para resolver a atividade. Escrever na lousa as diferentes estratégias encontradas na resolução da atividade, além de mostrar diferentes formas de resolução, auxilia no reconhecimento dos erros estratégicos do aluno para chegar ao resultado correto para saná-los, assim como identificar as dificuldades de compreensão dos conceitos estudados ou da proposta da própria atividade. Nesta atividade é importante também fazer o aluno perceber que dentre as 3 possíveis dimensões do pomar, embora elas possuíssem perímetros iguais, suas áreas diferentes.
Propósito: Compartilhamento de idéias e estratégias dos alunos na busca da resolução do problema, para a percepção dos erros nesse processo ou no da apropriação dos conceitos ensinados.
Discuta com a turma:
- Como vocês começaram a resolver o problema?
- Tinha como resolver a primeira parte sem ter que resolver também a segunda parte do problema?
- Então que estratégias vocês usaram?
Discussão da solução
Tempo sugerido: 10 minutos
Orientações: A discussão da atividade tem que ser dirigida pelo professor, onde serão organizados, sistematizados e resumidos os resultados e resoluções encontradas pelos alunos. Nesse momento da aula é importante promover a socialização das estratégias usadas pelos alunos para resolver a atividade. Escrever na lousa as diferentes estratégias encontradas na resolução da atividade, além de mostrar diferentes formas de resolução, auxilia no reconhecimento dos erros estratégicos do aluno para chegar ao resultado correto para saná-los, assim como, identificar as dificuldades de compreensão dos conceitos estudados ou da proposta da própria atividade. Nesta atividade é importante também fazer o aluno perceber que dentre as 3 possíveis dimensões do pomar, embora elas possuíssem perímetros iguais, suas áreas diferentes.
Propósito: Compartilhamento de idéias e estratégias dos alunos na busca da resolução do problema, para a percepção dos erros nesse processo ou no da apropriação dos conceitos ensinados.
Discuta com a turma:
- Como vocês começaram a resolver o problema?
- Tinha como resolver a primeira parte sem ter que resolver também a segunda parte do problema?
- Então que estratégias vocês usaram?
Discussão da solução
Tempo sugerido: 10 minutos
Orientações: A discussão da atividade tem que ser dirigida pelo professor, onde serão organizados, sistematizados e resumidos os resultados e resoluções encontradas pelos alunos. Nesse momento da aula é importante promover a socialização das estratégias usadas pelos alunos para resolver a atividade. Escrever na lousa as diferentes estratégias encontradas na resolução da atividade, além de mostrar diferentes formas de resolução, auxilia no reconhecimento dos erros estratégicos do aluno para chegar ao resultado correto para saná-los, assim como, identificar as dificuldades de compreensão dos conceitos estudados ou da proposta da própria atividade. Nesta atividade é importante também fazer o aluno perceber que dentre as 3 possíveis dimensões do pomar, embora elas possuíssem perímetros iguais, suas áreas diferentes.
Propósito: Compartilhamento de idéias e estratégias dos alunos na busca da resolução do problema, para a percepção dos erros nesse processo ou no da apropriação dos conceitos ensinados.
Discuta com a turma:
- Como vocês começaram a resolver o problema?
- Tinha como resolver a primeira parte sem ter que resolver também a segunda parte do problema?
- Então que estratégias vocês usaram?
Encerramento
Tempo sugerido: 3 minutos.
Orientação: Fazer um levantamento sobre o quê se aprendeu na aula sobre perímetro e área.
Raio X
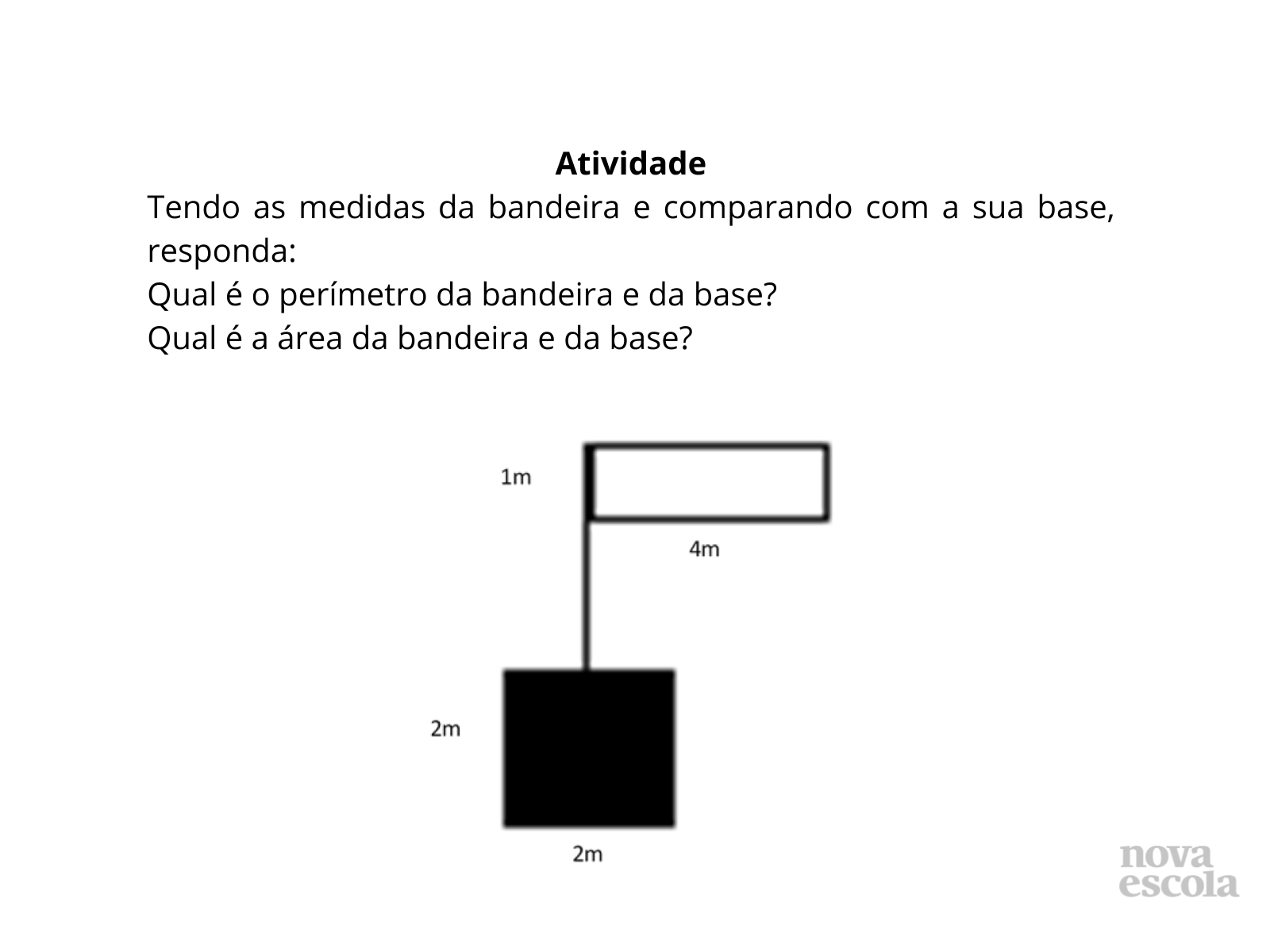
Tempo sugerido: 10 minutos.
Orientações: Nesta atividade os alunos terão uma situação um pouco diferente da atividade principal. Eles usarão os mesmos conhecimentos para realizá-la, mas agora individualmente. Essa atividade pode ser passada no quadro ou ser entregue em fotocópia, disponível no modelo de impressão. O Raio X é uma atividade avaliativa para verificar se o conteúdo dado foi aprendido pelos alunos e se conseguem progredir resolvendo um problema de maior complexidade. Para acessar o resultado da atividade veja o documento Resolução de raio x.
Propósito: Verificar se houve apropriação, por parte dos alunos, dos conceitos estudados na aula.
Discuta com a turma:
- Em relação à atividade feita na sala, foi muito diferente resolver essa? Por quê?
- Como vocês tentaram resolvê-lo?
Materiais complementares para impressão:
