Retomada
Plano de Aula
Plano de aula: Problemas de contagem: elaborando enunciados com restrições
Plano 4 de uma sequência de 5 planos. Veja todos os planos sobre Princípio multiplicativo da contagem
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Altamiro Marlon Ribeiro
Mentor: Amanda Ferreira Verardo Bilia
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
(EF08MA03): Princípio multiplicativo da contagem (resolução de problemas de contagem)
Conhecimentos prévios
Representar um diagrama de árvore, construir tabela de dupla entrada ou utilizar o princípio multiplicativo da contagem para solução de um problema.
Objetivos específicos
Resolver problemas de contagem com restrições elaboradas pelos estudantes, usando diagramas, tabelas ou princípio multiplicativo.
Conceito-chave
Contagem, elaboração de restrições, princípio multiplicativo da contagem.
Recursos necessários
- Projetor (caso haja)
- Atividades impressas em folhas, coladas no caderno ou não.
- Calculadora
Habilidades BNCC:
Objetivos de aprendizagem
Resolver problemas de contagem com restrições elaboradas pelos estudantes, usando diagramas, tabelas ou princípio multiplicativo.
Resumo da aula
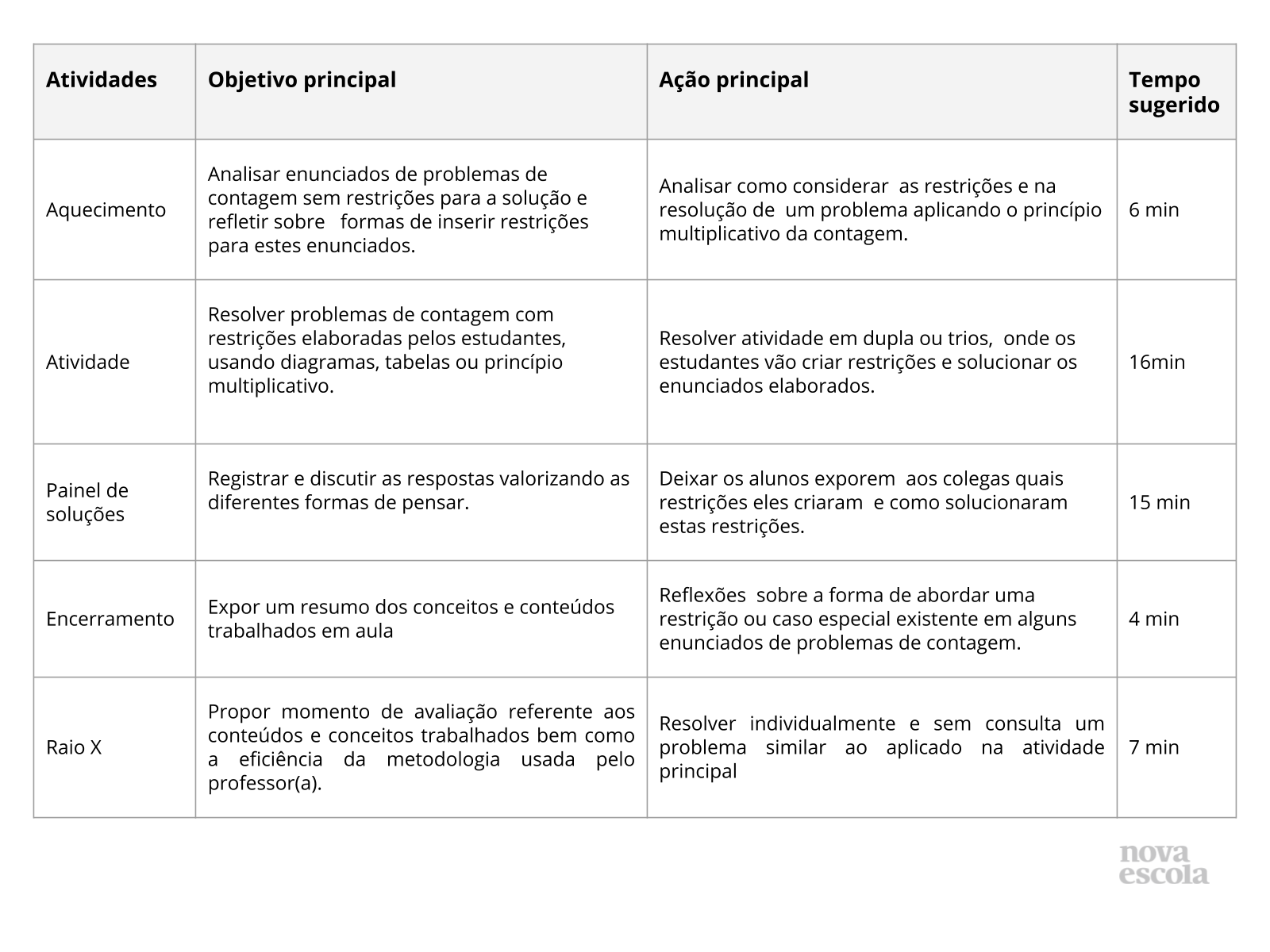
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Discuta com a Turma:
- De que formas podemos representar o princípio multiplicativo da contagem?
Sugestão de resposta: Para casos onde as soluções têm um número pequeno de agrupamentos ( combinações, possibilidades, sequências, etc.) podemos representar por diagramas de árvores ou tabelas, quando são soluções com um número muito grande de agrupamentos, calculamos só a quantidade, usando a multiplicação das decisões a serem tomada em cada etapa exigida pelo enunciado.
Retomada
Tempo sugerido: 6 minutos (slides 3, 4 e 5)
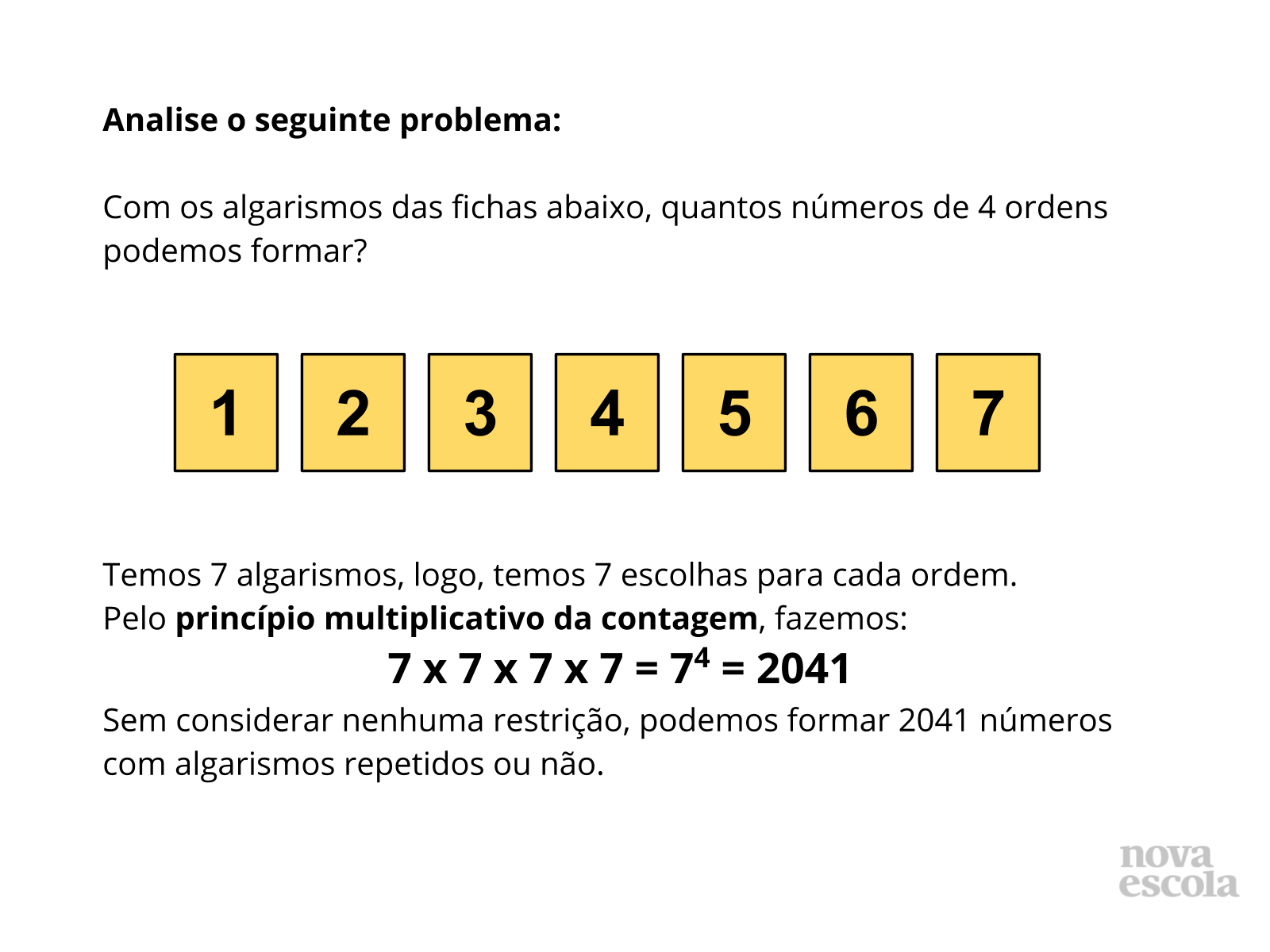
Orientação: Organize os alunos em duplas e de forma que não fiquem de costas uns para os outros. Projete o slide e/ou distribua cópias impressas da atividade, explique o texto (slide 3) para a turma, enfatizando que a quantidade de números encontrada é levando em consideração todos os casos que podem acontecer: números pares, ímpares, com e sem algarismos repetidos. No slide 4, os personagens sugerem restrições para o problema, isso certamente vai delimitar a quantidade de agrupamentos. Leia com a turma as restrições propostas e dê um tempo para a discussão de como trabalhar com elas na resolução do problema.
Propósito: Analisar a resolução de um problema de contagem sem considerar restrições para o enunciado.
Discuta com a turma:
- Para a situação do slide 3, seria prático encontrar o resultado representando o princípio multiplicativo da contagem através de um diagrama de árvore (grafo) ou uma tabela?
Sugestão de resposta: Não é prático pois demandaria muito tempo, problemas como esse, onde a solução engloba um número muito grande de agrupamentos, geralmente ficam restritos a determinar apenas quantos são eles.
- Quando há restrições no enunciado, p número de agrupamentos fica menor ou maior que o número que obtemos quando consideramos todos os casos possíveis? Justifique.
Sugestão de resposta: Quando o problema apresenta restrições, deixamos de fora alguns elementos dos conjuntos que estamos combinando / agrupando, portanto a quantidade final será sempre menor.
- Ao projetar o slide 4, peça para os estudantes sugerirem outras restrições para o problema.
Algumas restrições possíveis: Quantos são os números pares de quatro algarismos que podemos formar? Quantos números de quatro algarismos têm o número 7 na classe das centenas? Quantos são os números que os algarismos 1, 2 e 3 aparecem juntos nesta ordem?
Materiais complementares:
Retomada

Tempo sugerido: 6 minutos (slides 3, 4 e 5)
Orientação: Organize os alunos em duplas e de forma que não fiquem de costas uns para os outros. Projete o slide e/ou distribua cópias impressas da atividade, explique o texto (slide 3) para a turma, enfatizando que a quantidade de números encontrada é levando em consideração todos os casos que podem acontecer: números pares, ímpares, com e sem algarismos repetidos. No slide 4, os personagens sugerem restrições para o problema, isso certamente vai delimitar a quantidade de agrupamentos. Leia com a turma as restrições propostas e dê um tempo para a discussão de como trabalhar com elas na resolução do problema.
Propósito: Analisar a resolução de um problema de contagem sem considerar restrições para o enunciado.
Discuta com a turma:
- Para a situação do slide 3, seria prático encontrar o resultado representando o princípio multiplicativo da contagem através de um diagrama de árvore (grafo) ou uma tabela?
Sugestão de resposta: Não é prático pois demandaria muito tempo, problemas como esse, onde a solução engloba um número muito grande de agrupamentos, geralmente ficam restritos a determinar apenas quantos são eles.
- Quando há restrições no enunciado, p número de agrupamentos fica menor ou maior que o número que obtemos quando consideramos todos os casos possíveis? Justifique.
Sugestão de resposta: Quando o problema apresenta restrições, deixamos de fora alguns elementos dos conjuntos que estamos combinando / agrupando, portanto a quantidade final será sempre menor.
- Ao projetar o slide 4, peça para os estudantes sugerirem outras restrições para o problema.
Algumas restrições possíveis: Quantos são os números pares de quatro algarismos que podemos formar? Quantos números de quatro algarismos têm o número 7 na classe das centenas? Quantos são os números que os algarismos 1, 2 e 3 aparecem juntos nesta ordem?
Retomada

Tempo sugerido: 6 minutos (slides 3, 4 e 5)
Orientação: Organize os alunos em duplas e de forma que não fiquem de costas uns para os outros. Projete o slide e/ou distribua cópias impressas da atividade, explique o texto (slide 3) para a turma, enfatizando que a quantidade de números encontrada é levando em consideração todos os casos que podem acontecer: números pares, ímpares, com e sem algarismos repetidos. No slide 4, os personagens sugerem restrições para o problema, isso certamente vai delimitar a quantidade de agrupamentos. Leia com a turma as restrições propostas e dê um tempo para a discussão de como trabalhar com elas na resolução do problema.
Propósito: Analisar a resolução de um problema de contagem sem considerar restrições para o enunciado.
Discuta com a turma:
- Para a situação do slide 3, seria prático encontrar o resultado representando o princípio multiplicativo da contagem através de um diagrama de árvore (grafo) ou uma tabela?
Sugestão de resposta: Não é prático pois demandaria muito tempo, problemas como esse, onde a solução engloba um número muito grande de agrupamentos, geralmente ficam restritos a determinar apenas quantos são eles.
- Quando há restrições no enunciado, p número de agrupamentos fica menor ou maior que o número que obtemos quando consideramos todos os casos possíveis? Justifique.
Sugestão de resposta: Quando o problema apresenta restrições, deixamos de fora alguns elementos dos conjuntos que estamos combinando / agrupando, portanto a quantidade final será sempre menor.
- Ao projetar o slide 4, peça para os estudantes sugerirem outras restrições para o problema.
Algumas restrições possíveis: Quantos são os números pares de quatro algarismos que podemos formar? Quantos números de quatro algarismos têm o número 7 na classe das centenas? Quantos são os números que os algarismos 1, 2 e 3 aparecem juntos nesta ordem?
Materiais complementares:
Atividade principal

Tempo sugerido: 16 minutos (slides 6, 7 e 8)
Orientação:Projete o slide 6 e/ou leia as instruções para a atividade, e esclareça as possíveis dúvidas. Os slides 7 e 8 apresentam 2 situações em que os estudantes irão resolver-las (em duplas ou trios) sem considerar restrições (item A), elaborando ao menos 2 restrições para a situação e resolvendo-as (item B) e no item C, farão a comparação dos resultados com e sem restrições. Circule pela sala acompanhando o desempenho e envolvimento de cada um, observe as atitudes de colaboração entre os alunos e tire possíveis dúvidas para isso consulte o guia de intervenção. Neste momento de observação e intervenções, peça para eles explicarem suas soluções, principalmente para aqueles que precisam de mais auxílio para avançar. Quando as equipes estiverem elaborando as restrições para os casos, verifique se não estão colocando dificuldades muito complexas de serem resolvidas e também se estão determinando as respostas corretas, porém não valide nada ainda, a discussão e validação das respostas será feita no próximo momento da aula. Incentive-os a resolver suas propostas de diversas maneiras diferentes principalmente a mental para estimular o cálculo rápido.
Propósito: Analisar o enunciado de um problema de contagem, criar uma restrição ou caso especial para este enunciado e resolver o problema considerando a restrição inserida nele.
Discuta com a turma:
- Quando há uma restrição no problema, em que momento ela deve ser inserida na resolução?
Sugestão de resposta: Se uma das decisões a serem tomadas for mais restrita que as demais, essa é a decisão que deve ser tomada em primeiro lugar para evitar possíveis dificuldades na elaboração da solução. Tratando-se primeiro da restrição, o restante da resolução tende a ficar mais simples.
Materiais complementares:
Resolução da Atividade Principal
Atividade principal

Tempo sugerido: 16 minutos (slides 6, 7 e 8)
Orientação:Projete o slide 6 e/ou leia as instruções para a atividade, e esclareça as possíveis dúvidas. Os slides 7 e 8 apresentam 2 situações em que os estudantes irão resolver-las (em duplas ou trios) sem considerar restrições (item A), elaborando ao menos 2 restrições para a situação e resolvendo-as (item B) e no item C, farão a comparação dos resultados com e sem restrições. Circule pela sala acompanhando o desempenho e envolvimento de cada um, observe as atitudes de colaboração entre os alunos e tire possíveis dúvidas para isso consulte o guia de intervenção. Neste momento de observação e intervenções, peça para eles explicarem suas soluções, principalmente para aqueles que precisam de mais auxílio para avançar. Quando as equipes estiverem elaborando as restrições para os casos, verifique se não estão colocando dificuldades muito complexas de serem resolvidas e também se estão determinando as respostas corretas, porém não valide nada ainda, a discussão e validação das respostas será feita no próximo momento da aula. Incentive-os a resolver suas propostas de diversas maneiras diferentes principalmente a mental para estimular o cálculo rápido.
Propósito: Analisar o enunciado de um problema de contagem, criar uma restrição ou caso especial para este enunciado e resolver o problema considerando a restrição inserida nele.
Discuta com a turma:
- Quando há uma restrição no problema, em que momento ela deve ser inserida na resolução?
Sugestão de resposta: Se uma das decisões a serem tomadas for mais restrita que as demais, essa é a decisão que deve ser tomada em primeiro lugar para evitar possíveis dificuldades na elaboração da solução. Tratando-se primeiro da restrição, o restante da resolução tende a ficar mais simples.
Materiais complementares:
Atividade principal

Tempo sugerido: 16 minutos (slides 6, 7 e 8)
Orientação:Projete o slide 6 e/ou leia as instruções para a atividade, e esclareça as possíveis dúvidas. Os slides 7 e 8 apresentam 2 situações em que os estudantes irão resolver-las (em duplas ou trios) sem considerar restrições (item A), elaborando ao menos 2 restrições para a situação e resolvendo-as (item B) e no item C, farão a comparação dos resultados com e sem restrições. Circule pela sala acompanhando o desempenho e envolvimento de cada um, observe as atitudes de colaboração entre os alunos e tire possíveis dúvidas para isso consulte o guia de intervenção. Neste momento de observação e intervenções, peça para eles explicarem suas soluções, principalmente para aqueles que precisam de mais auxílio para avançar. Quando as equipes estiverem elaborando as restrições para os casos, verifique se não estão colocando dificuldades muito complexas de serem resolvidas e também se estão determinando as respostas corretas, porém não valide nada ainda, a discussão e validação das respostas será feita no próximo momento da aula. Incentive-os a resolver suas propostas de diversas maneiras diferentes principalmente a mental para estimular o cálculo rápido.
Propósito: Analisar o enunciado de um problema de contagem, criar uma restrição ou caso especial para este enunciado e resolver o problema considerando a restrição inserida nele.
Discuta com a turma:
- Quando há uma restrição no problema, em que momento ela deve ser inserida na resolução?
Sugestão de resposta: Se uma das decisões a serem tomadas for mais restrita que as demais, essa é a decisão que deve ser tomada em primeiro lugar para evitar possíveis dificuldades na elaboração da solução. Tratando-se primeiro da restrição, o restante da resolução tende a ficar mais simples.
Materiais complementares:
Discussão da solução

Tempo sugerido: 15 minutos (slides 9 e 10)
Orientação: Convide os alunos a irem para a lousa apresentar as restrições que criaram e suas resoluções. Incentive e medie a discussão sobre as diferentes restrições e soluções construídas. Neste momento, é importante que você discuta as resoluções e todos cheguem no resultado correto, caso haja alguma situação polêmica que você não esteja visualizando o resultado no momento, pesquise e entenda-a e traga a solução na próxima aula para otimizar o tempo, pois haverá uma diversidade grande de propostas e pretende-se que os estudantes aprendam a abordar todas elas na resolução de um problema de contagem. Consulte o arquivo onde consta a resolução da atividade principal, lá existe algumas restrições, além daquelas expostas aqui nos slides 9 e 10 para cada uma das situações. Procure organizar o tempo para que o máximo possível de enunciados e soluções sejam, compartilhados e discutidos.
Propósito: Promover a discussão das restrições e suas resoluções elaboradas pelos estudantes.
Materiais complementares:
Discussão da solução

Tempo sugerido: 15 minutos (slides 9 e 10)
Orientação: Convide os alunos a irem para a lousa apresentar as restrições que criaram e suas resoluções. Incentive e medie a discussão sobre as diferentes restrições e soluções construídas. Neste momento, é importante que você discuta as resoluções e todos cheguem no resultado correto, caso haja alguma situação polêmica que você não esteja visualizando o resultado no momento, pesquise e entenda-a e traga a solução na próxima aula para otimizar o tempo, pois haverá uma diversidade grande de propostas e pretende-se que os estudantes aprendam a abordar todas elas na resolução de um problema de contagem. Consulte o arquivo onde consta a resolução da atividade principal, lá existe algumas restrições, além daquelas expostas aqui nos slides 9 e 10 para cada uma das situações. Procure organizar o tempo para que o máximo possível de enunciados e soluções sejam, compartilhados e discutidos.
Propósito: Promover a discussão das restrições e suas resoluções elaboradas pelos estudantes.
Discuta com a turma:
- Como Funciona o rodízio de placas de automóveis na cidade de São Paulo?
Sugestão de resposta: O rodízio de placas é uma idéia aprovada pela população. Abrangendo caminhões e automóveis, esta regulamentação tem o objetivo de evitar que a situação do trânsito piore, pois nas grandes cidades um grandes problemas urbanos é o engarrafamento no trânsito devido ao considerável número de veículos de todas as categorias em circulação. Para saber mais acesse: http://www.cetsp.com.br/consultas/rodizio-municipal/como-funciona.aspx
Materiais complementares:
Encerramento

Tempo sugerido: 4 minutos
Orientação: Explique para a turma o texto do slide e certifique-se se ainda há dúvidas, em caso afirmativo esclareça-as, pois o próximo momento da aula é o RAIO X. Evidencie a forma de abordar uma restrição existente em um problema de contagem.
Propósito: Analisar a forma de abordar um problema de contagem quando nele existem restrições para a solução.
Discuta com a turma:
- No exemplo do texto, por que o zero não pode ocupar a primeira posição?
Atividade de Raio X

Tempo sugerido: 7 minutos
Orientação: Ler junto com os alunos, verificar se todos compreenderam o problema e sabem o que devem fazer, e pedir para que resolvam. Circule pela sala para verificar as resoluções. Lembre-se que neste momento você está avaliando os avanços dos estudantes em relação ao conteúdo da aula. Procure identificar as dúvidas que ainda ficaram e reserve os minutos finais da aula para uma breve correção desta atividade. Dê 5 minutos para a resolução e corrija em seguida.
Propósito: Verificar a assimilação dos conteúdos desenvolvidos durante a aula.
Materiais complementares:
Sugestão de adaptação para ensino remoto
Professor, revisite todos os arquivos do plano que você vai orientar e identifique os pontos principais para o trabalho remoto. Lembre-se que as sugestões precisam envolver tanto o uso da tecnologia quanto situações em que a tecnologia não está disponível.
Recursos
USAR APENAS FERRAMENTAS EM PORTUGUÊS E GRATUITAS.
- Necessários: papel e lápis.
- Opcionais: Meet, Hangout, Whatsapp, plataforma da Khan Academy (disponível aqui).
Para este plano, foque nas etapas AQUECIMENTO e ATIVIDADE PRINCIPAL.
Aquecimento
O aquecimento serve como exemplo para o uso de restrições nos problemas de contagem. O uso de restrições na ótica apresentada na aula funciona como uma reelaboração do problema. Por esta razão, é importante discuti-las. Você pode usar como proposta inicial e depois dar continuidade à Atividade Principal em outros momentos.
Atividade principal
A atividade principal pode ser realizada individualmente e remotamente, tanto com a situação A como a B (pode ser copiada ou impressa). Você pode optar por realizar o Aquecimento usando em seguida apenas uma das situações da Atividade Principal. Pode ainda dividir a turma em dois grupos: um faz a situação A e outro a situação B. Nestes problemas, é necessário elaborar uma restrição que altera o problema. Dessa forma, podem ser obtidos variados problemas que podem resultar numa ampla discussão.
Na plataforma da Khan Academy há vários vídeos e atividades sobre problemas de contagem. Essa pode ser uma proposta interessante para os alunos que têm acesso à Internet. Os vídeos a seguir são introdutórios para os problemas de combinação
Vídeo 1 (disponível aqui).
Vídeo 2 (disponível aqui).
Vídeo 3 (disponível aqui).
Discussão das soluções
Esta aula pode gerar diversos problemas diferentes, por isso, sugerimos categorizá-los para discutir os mais frequentes e relevantes. Provavelmente não haverá espaço e tempo para discutir cada um dos problemas reelaborados (com restrições) pelos alunos.
Você pode escolher um problema que tenha uma restrição interessante e um que tenha havido equívoco (da restrição elaborada ou da resposta) para disponibilizar aos alunos e acolher os comentários.
O Whatsapp pode ser usado para intermediar a mediação entre as respostas dos alunos, possíveis comentários e orientações sobre equívocos ou dúvidas apresentados. Se houver recursos tecnológicos para discussão em tempo real com a turma, utilize-os para esclarecer dúvidas e sugerir propostas que ampliem e consolidem as amprendizagens. Sugestão de recursos on line para discussões: Meet ou Hangout (Google).
Sistematização
xxx
Encerramento
xxx
Raio X
O Raio X pode ser usado como forma de revisão das aprendizagens, assim como as atividades complementares.
Convite às famílias
xxx
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Altamiro Marlon Ribeiro
Mentor: Amanda Ferreira Verardo Bilia
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
(EF08MA03): Princípio multiplicativo da contagem (resolução de problemas de contagem)
Conhecimentos prévios
Representar um diagrama de árvore, construir tabela de dupla entrada ou utilizar o princípio multiplicativo da contagem para solução de um problema.
Objetivos específicos
Resolver problemas de contagem com restrições elaboradas pelos estudantes, usando diagramas, tabelas ou princípio multiplicativo.
Conceito-chave
Contagem, elaboração de restrições, princípio multiplicativo da contagem.
Recursos necessários
- Projetor (caso haja)
- Atividades impressas em folhas, coladas no caderno ou não.
- Calculadora