Resumo da aula
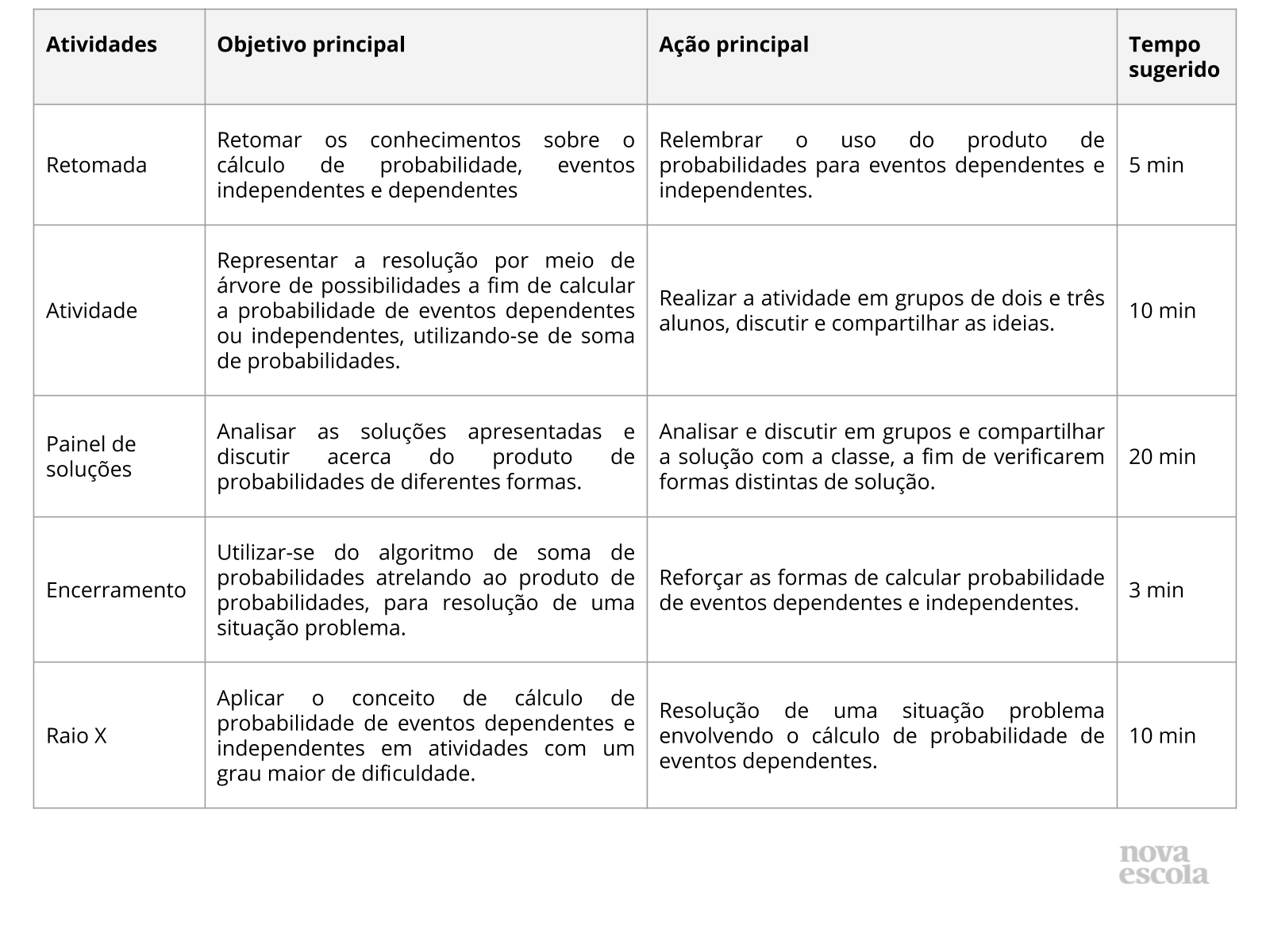
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
OBJETIVO

Tempo sugerido: 2 min
Orientação: Projete ou escreva na lousa.
Propósito: Apresentar para turma o objetivo da aula.
RETOMADA

Tempo sugerido: 5 min
Orientação: Lembre com os alunos que o produto de probabilidades é utilizado quando queremos saber a probabilidade de dois eventos acontecerem simultaneamente. Lembre-os que a representação matemática é dada por P(A interB)*.
Propósito: Relembrar o uso de produto de probabilidade.
Discuta com a turma:
- O que são eventos simultâneos?
- Qual a diferença entre eventos dependentes e independentes?
*não há como colocar o símbolo. Inter=interseção.
Materiais complementares para impressão:
Aquecimento
Resolução do aquecimento
ATIVIDADE PRINCIPAL

Tempo sugerido: 10 min
Orientação: Divida a turma em duplas para que possam discutir entre si as soluções. Peça aos alunos que façam suas anotações nos cadernos.
Circule pela sala observando as resoluções.
Propósito: Discutir formas de calcular a probabilidade de dois eventos dependentes.
Discuta com a turma:
- Qual tipo de evento estamos trabalhando?
- Podemos representar por árvore de probabilidade?
Materiais complementares para impressão:
Atividade principal
Resolução da Atividade principal
Guia de intervenção
DISCUSSÕES DA SOLUÇÃO

Tempo sugerido: 20 min. (slides 5, 6, 7 e 8)
Orientação: Questione aos alunos qual é o evento esperado. A resposta é obter R$1,25. Note que para alcançar o objetivo temos que fazer uma combinação de dois elementos, ou seja, tomar dois subconjuntos, uma vez que para formar o valor de R$1,25 precisamos ter a combinação de duas moedas. Questione aos alunos quais seriam esses dois elementos. Observe com os alunos que ao retirar uma moeda, pode sair o valor de R$ 0,25 ou R$1,00.
Para encontrarmos a solução, deve-se subdividir o cálculo em duas partes. Questione os alunos quais seriam as duas partes a serem analisadas.
Realize com os alunos uma árvore de possibilidades.
Propósito: Discutir formas de calcular a probabilidade de dois eventos dependentes.
Discuta com a turma:
- Quais as possibilidades podem ocorrer?
DISCUSSÕES DA SOLUÇÃO
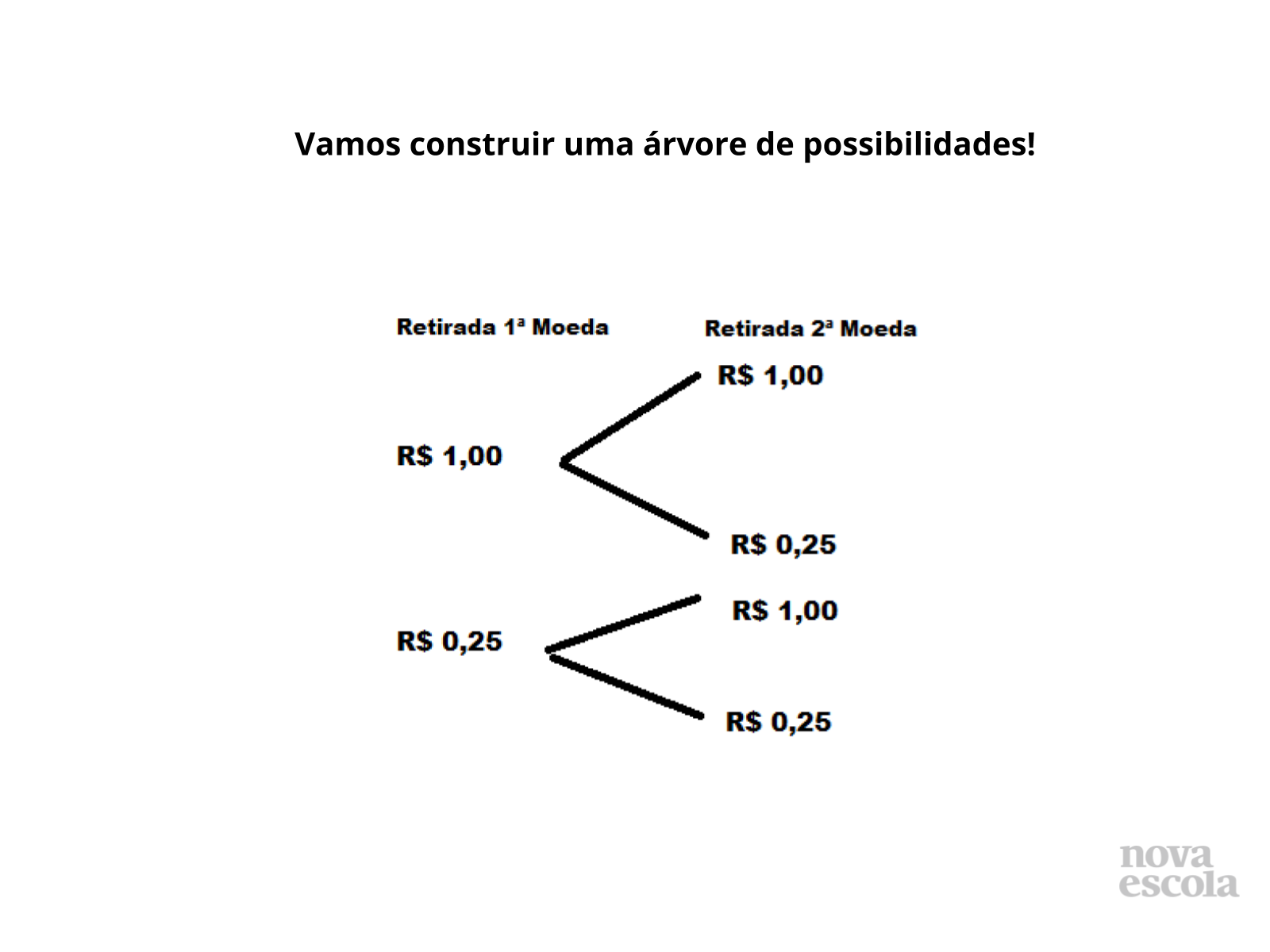
Tempo sugerido: 20 min. (slides 5, 6, 7 e 8)
Orientação: Apenas mostre o slide depois de constatar com os alunos as perguntas abaixo. Anote na lousa as respostas para que todos possam discutir.
Quais são as possibilidades na primeira retirada? Observe com os alunos que na primeira retirada pode ocorrer de sair a moeda com o valor de R$1,00 ou de R$ 0,25
Pergunte aos alunos quais são as possibilidades da segunda retirada, se sair a primeira moeda o valor de R$1,00 e quais seriam as possibilidades da segunda retirada caso saísse uma moeda com o valor de R$ 0,25
Propósito: Apresentar a solução por meio de árvores de probabilidades.
Discuta com a turma:
- A forma de representar por meio árvores facilita a compreensão desse tipo de problema?
- Podem ocorrer de sair tanto uma moeda como a outra, por isso devemos considerar os dois casos?
DISCUSSÃO DA SOLUÇÃO

Tempo sugerido: 20 min. (slides 5, 6, 7 e 8)
Orientação: O objetivo é trabalhar com todas as probabilidades de cada “galho” da árvore. Comece questionando aos alunos qual seria a probabilidade de sair uma moeda de R$1,00 na primeira retirada. Espera-se que os alunos tenham observado que a probabilidade é de 30/50 ou ?. Questione também, a probabilidade de sair uma moeda de R$0,25 que é de 20/50 ou ?.
Observe com os alunos que saindo uma moeda de R$ 1,00 em seguida podem sair ou uma moeda de R$1,00 (já que não houve reposição) ou uma moeda de R$ 0,25. As probabilidades são, respectivamente: 29/49 e 20/49.
No segundo caso, se tiver saído uma moeda de R$ 0,25, podem sair uma moeda R$1,00 ou R$ 0,25 (não houve reposição). As probabilidades são respectivamente: 30/49 e 19/49. Agora questione aos alunos se iremos utilizar todos os valores para o resultado final. Observe que queremos apenas formar o valor de R$ 1,25 e deste modo temos que usar o que nos convém.
Propósito: Analisar as possibilidades da retirada das moedas.
Discuta com a turma:
- São eventos dependentes ou independentes?
- O que acontece quando não há reposição?
- Será necessário saber todas as probabilidades?
DISCUSSÕES DA SOLUÇÃO

Tempo sugerido: 20 min. (slides 5, 6, 7 e 8)
Orientação: Professor, anote os valores na lousa, seguindo o raciocínio com os alunos.
Neste caso, mostre aos alunos que o que nos interessa, que são os galhos que formam o valor de R$ 1,25. No primeiro caso, consideraremos sair R$1,00 na primeira retirada e R$0,25 na segunda retirada. Temos que a probabilidade de sair R$1,25 é o produto entre as duas probabilidades, isto é: ? * 20/49 =60/245=0.24 ou 24%. No segundo caso, consideraremos sair uma moeda de R$0,25 na primeira retirada e R$ 1,00 na segunda, logo a probabilidade é dada por: ? * 30/49 = 60/245 = 0,24 ou 24%. No entanto ressalte aos alunos que temos duas formas de acontecer, neste caso o que se deve fazer no final? Os alunos devem responder que deverão somar as probabilidades, tendo então 0,24+0,24= 0,48 ou 48%
Propósito: Apresentar a solução por meio de árvores de probabilidades.
Discuta com a turma:
- A forma de representar por meio árvores facilita a compreensão desse tipo de problema?
- Quais são as possibilidades?
- Por que o valor está próximo de 50%?
ENCERRAMENTO

Tempo sugerido: 3 min
Orientação: Leia ou projete.
Propósito: Finalizar a aula resumindo sobre o uso de produto de probabilidade atrelado ao uso de soma de probabilidades.
RAIO X

Tempo sugerido: 10 min.
Orientação: Observe com os alunos que o exercício é similar ao da atividade principal, no entanto não queremos um valor exato. Queremos apenas que saiam duas moedas de mesmo valor.
Propósito: Aplicar os conhecimentos aprendidos na aula.
Discuta com a turma:
- Podemos pensar da mesma forma que a atividade anterior?
- Que possibilidade devemos considerar?
Materiais complementares para impressão:
Raio X
Resolução do Raio X
Atividade complementar
Resolução da Atividade complementar
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.