Retomada
Plano de Aula
Plano de aula: Resolvendo problemas com múltiplos comuns
Plano 9 de uma sequência de 10 planos. Veja todos os planos sobre Números primos e compostos
Por: Allan Costa Jardim
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Allan Costa Jardim
Mentor: Rodrigo Morozetti Blanco
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
(EF06MA05) Resolver e elaborar problemas que envolvam as ideias de múltiplo e de divisor;
Objetivos específicos
Identificar múltiplos comuns a dois números naturais.
Observar que estes conjuntos contém um menor elemento e não contém maior elemento.
Desenvolver estratégias para se encontrar o menor múltiplo comum a dois (ou mais) números naturais dados.
Resolver problemas envolvendo múltiplos comuns a dois ou mais números.
Conceito-chave
Múltiplos Comuns, Divisibilidade, Resolução de Problemas.
Recursos necessários
- Atividades impressas em folhas, coladas no caderno ou não.
- Lápis e borracha.
Habilidades BNCC:
Objetivos de aprendizagem
Identificar múltiplos comuns a dois números naturais.
Observar que estes conjuntos contém um menor elemento e não contém maior elemento.
Desenvolver estratégias para se encontrar o menor múltiplo comum a dois (ou mais) números naturais dados.
Resolver problemas envolvendo múltiplos comuns a dois ou mais números.
Resumo da aula
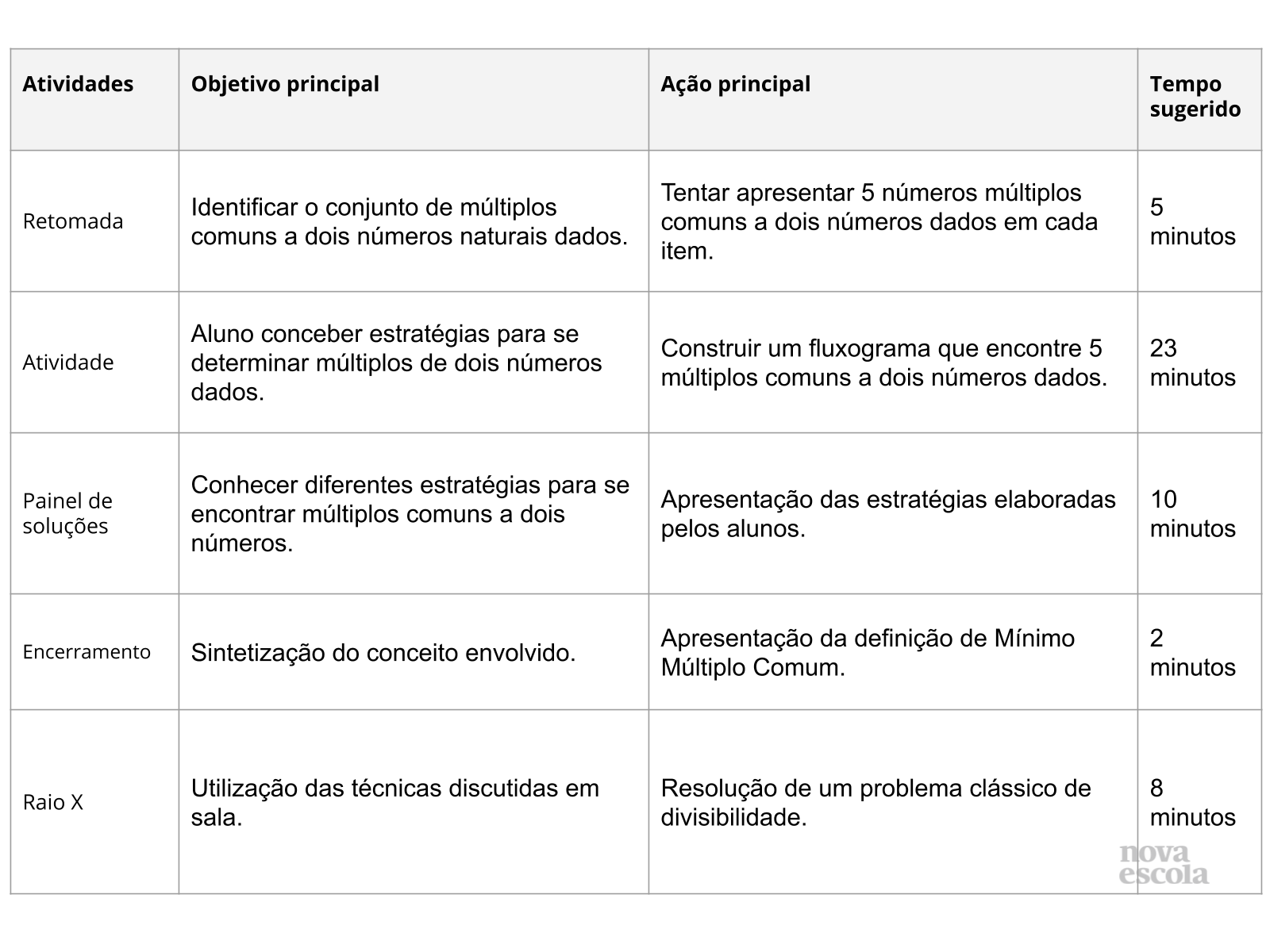
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
OBJETIVO

TEMPO SUGERIDO: 2 MINUTOS
ORIENTAÇÕES: Leia o objetivo com a turma, seja projetando via projetor multimídia e/ou imprimindo o objetivo para ser colado no caderno de cada aluno.
PROPÓSITO: Compartilhar com a turma o objetivo a ser atingido nesta aula.
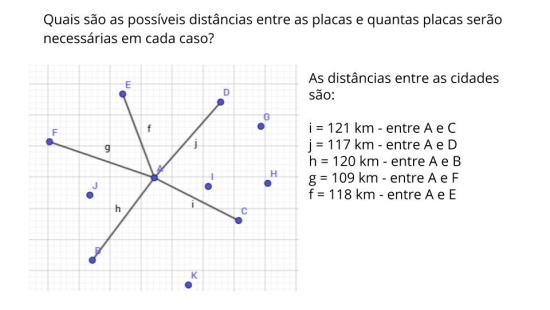
ATIVIDADE DE RETOMADA

TEMPO SUGERIDO: 5 minutos
ORIENTAÇÕES:
- Para esta atividade, sugere-se que o professor acompanhe as estratégias utilizadas pelos alunos, visto que eles ainda não estudaram os Múltiplos Comuns, tampouco o Mínimo Múltiplo Comum.
- É possível que as estratégias elaboradas, sejam as mais imediatas. Não há problemas em os alunos concebam esse tipo de estratégia neste momento.
- Não iniba a construção de múltiplos comuns muito grandes por parte dos alunos. Esse momento ainda é de descoberta, portanto, permita-os proporem soluções diversas para o problema.
PROPÓSITO: Apresentar aos alunos a atividade de retomada da aula.
DISCUTA COM A TURMA:
- Como vocês resolveram o problema? Quais caminhos vocês adotaram?
MATERIAIS COMPLEMENTARES
ATIVIDADE PRINCIPAL (slide 4 e 5)
TEMPO SUGERIDO: 23 minutos
ORIENTAÇÕES:
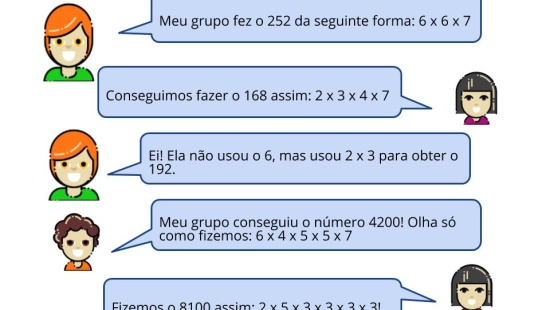
- O item a) da atividade certamente trará múltiplos diferentes dos obtidos pelos alunos na atividade de retomada. Utilize essas divergências para questioná-los a respeito do que poderia ter sido diferente em cada técnica empregada.
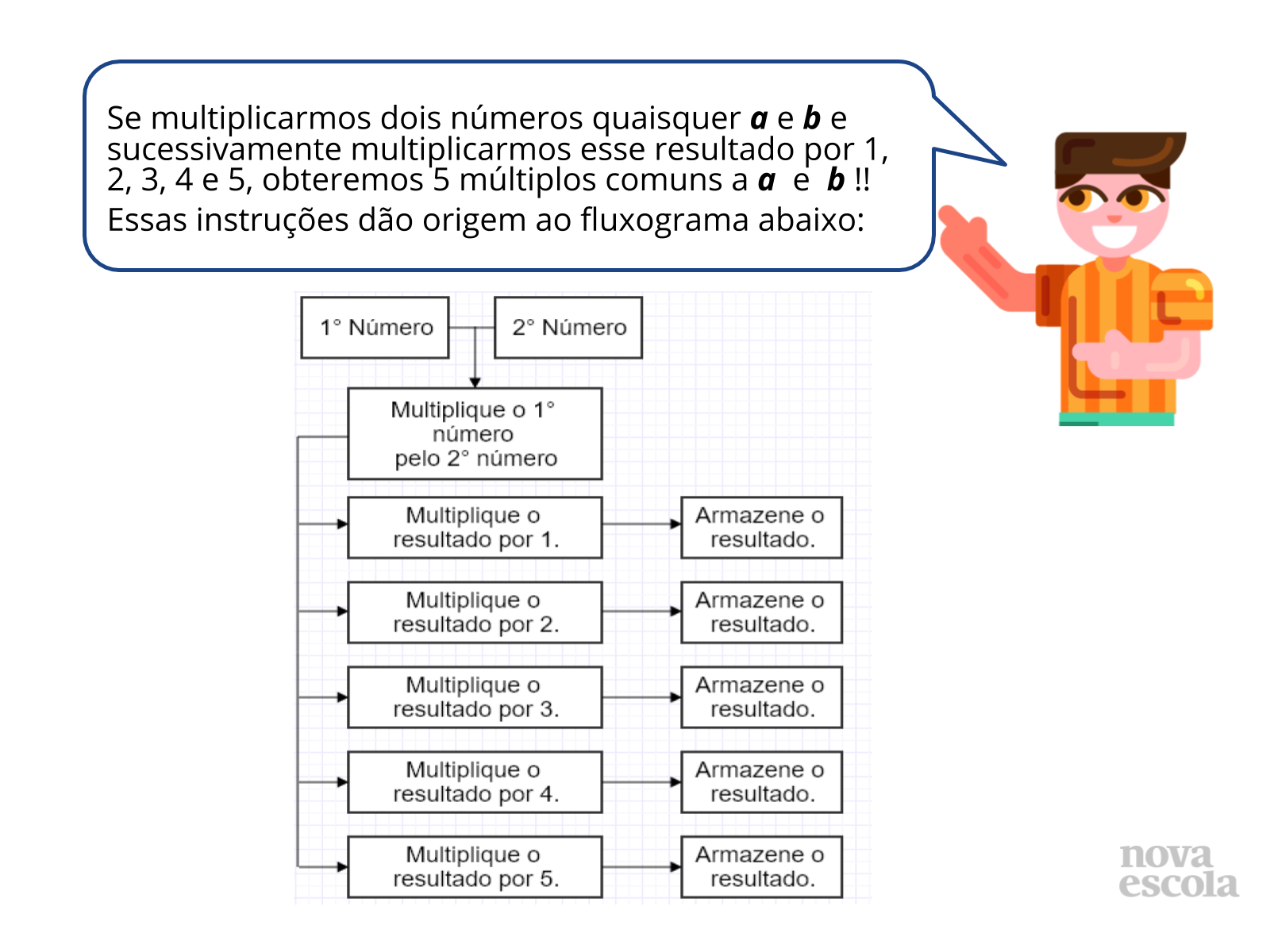
- Espera-se que os alunos já tenham alguma experiência com fluxogramas, afinal, há planos de aulas anteriores tratando sobre o assunto.
Sobre a atividade do slide 5:
- Sugere-se que divida a sala em grupos (podendo ser trios ou quartetos) de forma que alguns grupos fiquem com a elaboração do fluxograma e os demais fiquem responsáveis por calcular os 5 menores múltiplos comuns em cada item da atividade de retomada. Caso essa seja a opção de divisão da turma, na sessão de discussão da solução promova a apresentação dos fluxograma e discussão de resultados em conjunto com o grupo de alunos que buscou os 5 menores múltiplos comuns da atividade de retomada. Essa interação fará com que os alunos cheguem a versões melhoradas dos fluxogramas apresentados.
- Existem várias possibilidades de elaboração de fluxograma na atividade do slide 5, desde utilizando decomposição em fatores primos a criar conjuntos de múltiplos e comparando os múltiplos dos dois conjuntos. Portanto, permita que os alunos desenvolvam o caminho que julgarem mais conveniente.
PROPÓSITO: Apresentar aos alunos a atividade principal da aula.
DISCUTA COM A TURMA:
- Você encontrou diferenças entre as respostas que foram obtidas com o fluxograma que contém as instruções do Ramon e as respostas que foram encontradas na Atividade de Retomada? Porquê?
- Por que seu grupo optou por este caminho na confecção deste fluxograma?
- Quais os procedimentos que vocês usaram para encontrar os 5 menores múltiplos comuns a cada par de números dado na atividade de retomada?
- O conjunto dos múltiplos de um par de números tem um maior elemento?
MATERIAIS COMPLEMENTARES
Resolução da Atividade Principal
ATIVIDADE PRINCIPAL (slide 4 e 5)

TEMPO SUGERIDO: 23 minutos
ORIENTAÇÕES:
- O item a) da atividade certamente trará múltiplos diferentes dos obtidos pelos alunos na atividade de retomada. Utilize essas divergências para questioná-los a respeito do que poderia ter sido diferente em cada técnica empregada.
- Espera-se que os alunos já tenham alguma experiência com fluxogramas, afinal, há planos de aulas anteriores tratando sobre o assunto.
Sobre a atividade do slide 5:
- Sugere-se que divida a sala em grupos (podendo ser trios ou quartetos) de forma que alguns grupos fiquem com a elaboração do fluxograma e os demais fiquem responsáveis por calcular os 5 menores múltiplos comuns em cada item da atividade de retomada. Caso essa seja a opção de divisão da turma, na sessão de discussão da solução promova a apresentação dos fluxograma e discussão de resultados em conjunto com o grupo de alunos que buscou os 5 menores múltiplos comuns da atividade de retomada. Essa interação fará com que os alunos cheguem a versões melhoradas dos fluxogramas apresentados.
- Existem várias possibilidades de elaboração de fluxograma na atividade do slide 5, desde utilizando decomposição em fatores primos a criar conjuntos de múltiplos e comparando os múltiplos dos dois conjuntos. Portanto, permita que os alunos desenvolvam o caminho que julgarem mais conveniente.
PROPÓSITO: Apresentar aos alunos a atividade principal da aula.
DISCUTA COM A TURMA:
- Você encontrou diferenças entre as respostas que foram obtidas com o fluxograma que contém as instruções do Ramon e as respostas que foram encontradas na Atividade de Retomada? Porquê?
- Por que seu grupo optou por este caminho na confecção deste fluxograma?
- Quais os procedimentos que vocês usaram para encontrar os 5 menores múltiplos comuns a cada par de números dado na atividade de retomada?
- O conjunto dos múltiplos de um par de números tem um maior elemento?
MATERIAIS COMPLEMENTARES
Resolução da Atividade Principal
Acesse aqui um texto com outras atividades envolvendo múltiplos e divisores
Acesse aqui uma apresentação explicando o uso dos blocos em fluxogramas
PAINEL DE SOLUÇÕES (slides 6 e 7)

TEMPO SUGERIDO: 10 minutos
ORIENTAÇÕES:
- Nos slides são apresentadas algumas possibilidades de respostas. Podem ocorrer outras, de acordo com a criatividade dos alunos.
- Peça aos alunos para testarem cada fluxograma com os pares de números da atividade de retomada, bem como os menores múltiplos comuns em cada item.
- Incentive-os a expor os fluxogramas apresentados, mas, mais importante será a razão pela qual aquele caminho foi proposto como solução.
PROPÓSITO: Discutir as soluções apresentadas pelos alunos.
DISCUTA COM A TURMA:
- Os resultados obtidos no fluxograma coincidem com os mínimos múltiplos comuns em cada item da atividade de retomada?
- Será possível determinar múltiplos de dois números utilizando a decomposição em fatores primos?
- O que mudaria no seu fluxograma se fossem dados 3 números ao invés de 2?
- Você consegue encontrar um padrão para determinar o menor múltiplo comum quando os números não possuem divisores comuns? E quando um é múltiplo do outro? E quando um não é múltiplo do outro, mas ambos são múltiplos de um mesmo número?
PAINEL DE SOLUÇÕES (slides 6 e 7)

TEMPO SUGERIDO: 10 minutos
ORIENTAÇÕES:
- Nos slides são apresentadas algumas possibilidades de respostas. Podem ocorrer outras, de acordo com a criatividade dos alunos.
- Peça aos alunos para testarem cada fluxograma com os pares de números da atividade de retomada, bem como os menores múltiplos comuns em cada item.
- Incentive-os a expor os fluxogramas apresentados, mas, mais importante será a razão pela qual aquele caminho foi proposto como solução.
PROPÓSITO: Discutir as soluções apresentadas pelos alunos.
DISCUTA COM A TURMA:
- Os resultados obtidos no fluxograma coincidem com os mínimos múltiplos comuns em cada item da atividade de retomada?
- Será possível determinar múltiplos de dois números utilizando a decomposição em fatores primos?
- O que mudaria no seu fluxograma se fossem dados 3 números ao invés de 2?
- Você consegue encontrar um padrão para determinar o menor múltiplo comum quando os números não possuem divisores comuns? E quando um é múltiplo do outro? E quando um não é múltiplo do outro, mas ambos são múltiplos de um mesmo número?
ENCERRAMENTO

TEMPO SUGERIDO: 2 minutos
ORIENTAÇÕES:
- Destaque que há infinitos múltiplos comuns a dois (ou mais) números inteiros, entretanto, sempre haverá um que será o menor.
- Relembre-os que a expressão “múltiplo de” é equivalente a “divisível por”. Em outras palavras, o Mínimo Múltiplo comum também pode ser visto como o menor número divisível por dois (ou mais) números dados.
PROPÓSITO: Sintetizar o conceito principal da aula.
ATIVIDADE RAIO X

TEMPO SUGERIDO: 8 minutos
ORIENTAÇÕES:
- Essa atividade está inspirada em um problema apresentado no livro “O Homem que Calculava” do escritor e professor Malba Tahan (pseudônimo adotado pelo professor brasileiro Júlio César de Melo e Sousa). O texto completo do problema que envolve frações está em link abaixo na seção “Materiais Complementares”. Caso consiga tempo, vale a pena contar a história toda.
- A atividade permite uma conexão com as adições de frações. Sugere-se que, caso haja tempo, após a conclusão da atividade pelos alunos, que sejam calculadas as quantidades envolvidas: metade, um terço e um nono da herança e ao final, que se somem os resultados.
- Esse problema apresenta uma sutil diferença entre os demais problemas de múltiplos comuns, ele pede que sejam encontrados números que sejam divisíveis por 2, 3 e 9. Que em síntese são múltiplos comuns a estes números. Essa diferença na apresentação merece atenção e trataremos dessa possibilidade no Guia de Intervenção.
PROPÓSITO: Apresentar aos alunos uma atividade básica para aplicação da técnica.
DISCUTA COM A TURMA:
- 35 é divisível por 2, 3 e 9? A herança seria dividida de forma exata com estas frações envolvidas?
MATERIAIS COMPLEMENTARES
Resolução da atividade complementar
Fluxogramas, Algoritmos, Matemática e Tecnologia
Acesse aqui um site contendo o texto do problema dos 35 camelos, citado nesta atividade.
Código do plano: MAT6_03NUM09
Recursos
- Necessários: Caderno, lápis, borracha, grupo de whatsapp
- Opcionais: -
Para este plano, foque na etapa: Retomada e Atividade Complementar
Retomada
Professor, nessa proposta sugerimos o recurso da aula invertida. Para isso, os alunos precisam ter acesso às atividades propostas na Retomada com antecedência. Você pode propor os questionamentos apresentados no slide usando um editor de texto (Google Docs, por exemplo) ou outro meio de comunicação combinado entre vocês. Peça aos alunos que registrem suas resoluções e estratégias no caderno para que possam consulta-las durante a aula.
Discussão das soluções + Atividade Complementar
Ao iniciar a aula, organize um espaço de compartilhamento e discussão das resoluções (fórum, mensagens de WhatsApp, ou outra plataforma de interação). Essa é uma etapa importantíssima da aula, pois nela os alunos irão justificar as estratégias e respostas das atividades. Estimule os alunos a analisar e comparar as respostas compartilhadas pelos colegas. Peça que acionem seus microfones e expliquem como pensaram para atender o que foi solicitado. Valorize as estratégias dos alunos e use-as como ponto de partida para dar continuidade à discussão das soluções. Para isso, compartilhe com os alunos por mensagem de texto apenas o primeiro exercício da atividade complementar:
Lucas recebe a visita do seu avô Dimas a cada 15 dias. Alexandre, o tio dele, o visita a cada 10 dias e, devido às escalas de trabalho, a cada 12 dias Lucas vai à praia com seus pais. Um belo dia Lucas recebeu a visita do seu avô, do seu tio e foi à praia com seus pais (e com o avô e o tio que o visitavam neste dia). Quantos dias depois este acontecimento se repetirá?
Comece questionando o que eles entenderam sobre o problema e o que eles acham que é preciso fazer para resolvê-lo. Faça com que eles percebam a importância de relacionar o que foi pedido com os conhecimentos prévios deles sobre múltiplo, divisores e números primos. Lembre-se que o objetivo da aula é que os alunos resolvam problemas com múltiplos comuns a dois ou mais números inteiros.
Para isso, invista em boas perguntas: “Vocês percebem alguma relação desse problema com os conceitos de múltiplos e divisores?”, “Será que há alguma relação entre esse problema e a atividade que vocês fizeram antes da aula, quando calcularam múltiplos comuns?” A partir dessas perguntas e outras que surgirão a partir das respostas dos alunos, peça aos alunos que resolvam o problema. Dê a eles alguns minutos e na retomada organize um fórum para que eles possam compartilhar suas estratégias e resoluções. Nesse fórum, os alunos podem enviar mensagens de áudio ou texto, combine com eles o que for mais prático para o grupo. A partir das respostas que você obtiver dos alunos, encaminhe para o encerramento, garantindo que eles compreendam a necessidade de analisar os múltiplos de cada quantidade de dias e identificar o múltiplo que é comum às três quantidades.
Convite às famílias
Peça às famílias que, oportunamente, auxiliem na leitura das comandas e no envio das soluções, conforme os combinados com o professor. É importante que as famílias acompanhem as atividades nos canais de comunicação estabelecidos entre vocês.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Allan Costa Jardim
Mentor: Rodrigo Morozetti Blanco
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
(EF06MA05) Resolver e elaborar problemas que envolvam as ideias de múltiplo e de divisor;
Objetivos específicos
Identificar múltiplos comuns a dois números naturais.
Observar que estes conjuntos contém um menor elemento e não contém maior elemento.
Desenvolver estratégias para se encontrar o menor múltiplo comum a dois (ou mais) números naturais dados.
Resolver problemas envolvendo múltiplos comuns a dois ou mais números.
Conceito-chave
Múltiplos Comuns, Divisibilidade, Resolução de Problemas.
Recursos necessários
- Atividades impressas em folhas, coladas no caderno ou não.
- Lápis e borracha.