Código do plano: MAT6_03NUM10
Recursos
- Necessários: Caderno, lápis, borracha, grupo de WhatsApp
- Opcionais: -
Para este plano, foque na etapa: Retomada e Atividade Principal
Retomada
Professor, nessa proposta sugerimos o recurso da aula invertida. Para isso, os alunos precisam ter acesso às atividades propostas na Retomada com antecedência. Você pode propor os questionamentos apresentados no slide usando um editor de texto (Google Docs, por exemplo) ou outro meio de comunicação combinado entre vocês. Peça aos alunos que registrem suas resoluções e estratégias no caderno para que possam consulta-las durante a aula.
Discussão das soluções + Atividade Complementar
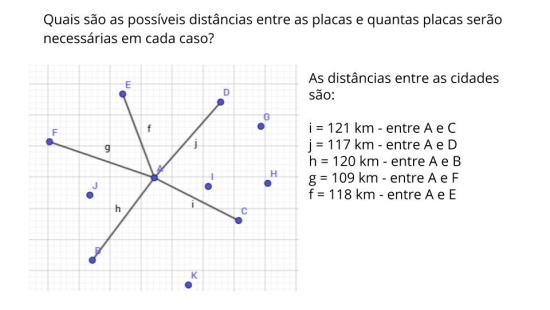
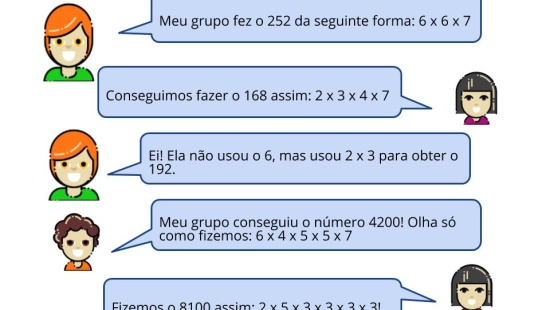
Ao iniciar a aula, organize um espaço de compartilhamento e discussão das resoluções (fórum, mensagens de WhatsApp, ou outra plataforma de interação). Essa é uma etapa importantíssima da aula, pois nela os alunos irão justificar as estratégias e respostas das atividades. Estimule os alunos a analisar e comparar as respostas compartilhadas pelos colegas. Peça que acionem seus microfones e expliquem como pensaram para atender o que foi solicitado na atividade enviada previamente. Valorize as estratégias dos alunos e use-as como ponto de partida para dar continuidade à discussão das soluções. Ao terminar essa etapa, compartilhe com os alunos o slide da Atividade Principal. Comece questionando o que eles entenderam sobre o problema e o que eles acham que é preciso fazer para resolvê-lo. Faça com que eles percebam a importância de relacionar o que foi pedido com os conhecimentos prévios deles sobre múltiplo, divisores e números primos. Lembre-se que um dos objetivos da aula é que os alunos resolvam problemas com divisores comuns.
Para isso, invista em boas perguntas: “Vocês percebem alguma relação desse problema com o conceito de divisor?”, “Será que há alguma relação entre esse problema e a atividade que vocês fizeram antes da aula, quando calcularam divisores comuns?”. A partir dessas perguntas e outras que surgirão a partir das respostas dos alunos, peça aos alunos que resolvam o problema. Dê a eles alguns minutos e na retomada organize um fórum para que eles possam compartilhar suas estratégias e resoluções. Nesse fórum, os alunos podem enviar mensagens de áudio ou texto, combine com eles o que for mais prático para o grupo. A partir das respostas que você obtiver dos alunos, encaminhe para o encerramento, garantindo que eles compreendam a necessidade de analisar os divisores de cada quantidade e identificar o divisor que é comum às três quantidades.
Caso sua aula não seja síncrona, organize o compartilhamento das propostas e a interação pelo WhatsApp ou outra plataforma de interação combinada entre vocês.
Convite às famílias
Peça às famílias que, oportunamente, auxiliem na leitura das comandas e no envio das soluções, conforme os combinados com o professor. É importante que as famílias acompanhem as atividades nos canais de comunicação estabelecidos entre vocês.