Atividade de aquecimento
Plano de Aula
Plano de aula: Explorando distâncias e caminhos no plano cartesiano
Plano 5 de uma sequência de 11 planos. Veja todos os planos sobre Teorema de Pitágoras e suas aplicações
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Sebastiao Rodrigues da Silva
Mentor: Lara Martins Barbosa
Especialista de área: Pricilla Mendes Cerqueira
Habilidade da BNCC
(EF09MA14) Resolver e elaborar problemas de aplicação do teorema de Pitágoras ou das relações de proporcionalidade envolvendo retas paralelas cortadas por secantes.
Objetivos específicos
Aplicar o teorema de Pitágoras para determinar a distância entre dois pontos no plano cartesiano.
Conceito-chave
Utilização do Teorema de Pitágoras como conceito auxiliar no cálculo de distâncias entre pontos no plano cartesiano
Recursos necessários
- Lápis, régua.
- Malha quadriculada
- Atividades impressas.
Habilidades BNCC:
Objetivos de aprendizagem
Aplicar o teorema de Pitágoras para determinar a distância entre dois pontos no plano cartesiano.
Resumo da aula
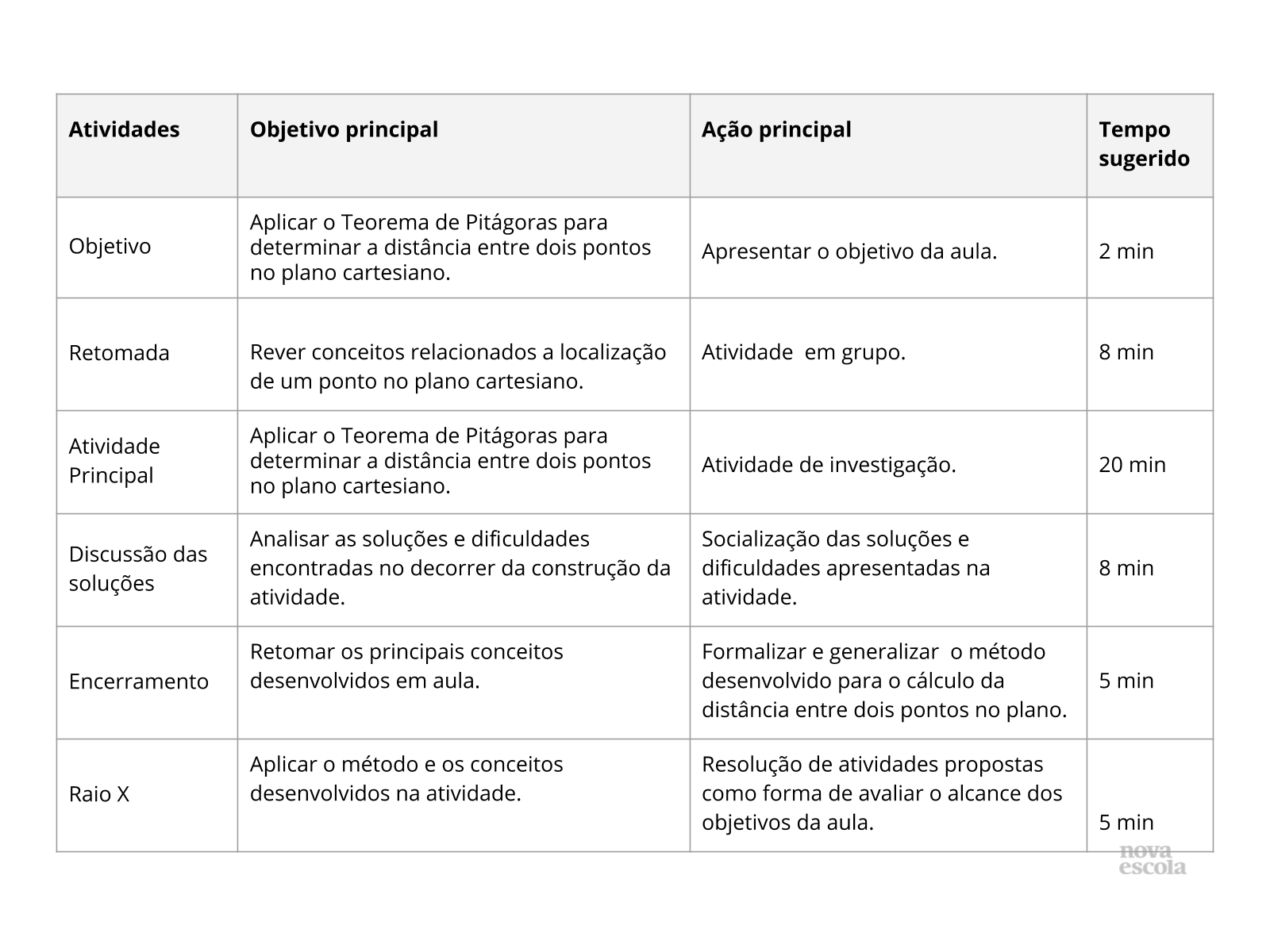 Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientações: Apresente o objetivo da aula de forma clara, de modo que os alunos percebam o que se deseja alcançar com as atividades a serem desenvolvidas na aula.
Propósito: Apresentar o objetivo da aula.
Discuta com a turma:
- Como se representa um ponto no plano cartesiano
- O que significa “ determinar a distância entre dois pontos, no plano cartesiano?
Retomada
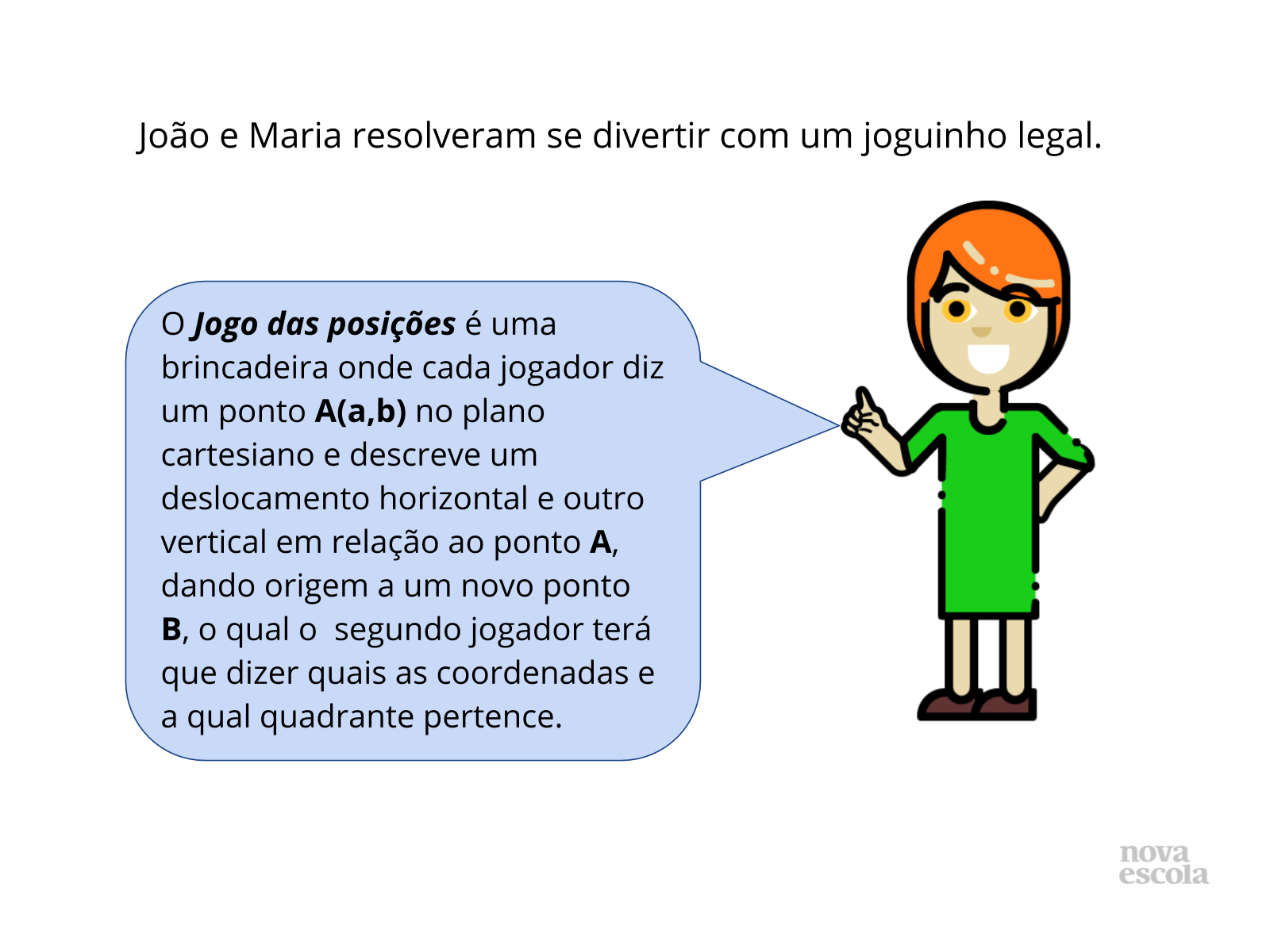
Tempo sugerido: 8 minutos. (slides 3, 4, 5 e 6 ).
Orientações:
Organize a turma em equipes de 3 alunos, para que possam interagir no desenvolvimento da atividade. Disponibilize folha quadriculadas para que a atividade seja realizada de forma mais satisfatória e dentro do tempo previsto.
Propósito: Rever conceitos relacionados a localização de um ponto no plano cartesiano, bem como localizar pontos a partir de um ponto dado, através de “deslocamentos” horizontais e verticais.
Discuta com a turma:
- O que é um plano cartesiano?
- Por que é chamado de cartesiano?
Materiais complementares para impressão:
Retomada

Tempo sugerido: 8 minutos. (slides 3, 4,5 e 6 ).
Orientações:
Exponha de forma clara a distribuição dos pontos após cada rodada.
Propósito: Rever conceitos relacionados a localização de um ponto no plano cartesiano, bem como localizar pontos a partir de um ponto dado, através de “deslocamentos” horizontais e verticais.
Discuta com a turma:
- Qual o significado das coordenadas a e b em um ponto A(a,b) no plano cartesiano?
Retomada

Tempo sugerido: 8 minutos. (slides 3, 4,5 e 6 ).
Orientações:
Observe se cada roda está sendo representada em um plano cartesiano específico, do contrário, oriente os alunos para representarem dessa forma.
Propósito: Rever conceitos relacionados a localização de um ponto no plano cartesiano, bem como localizar pontos a partir de um ponto dado, através de “deslocamentos” horizontais e verticais.
Discuta com a turma:
- Deslocamentos para cima representam “andar” paralelo a qual eixo? No sentido positivo ou negativo?
- Deslocamentos para a esquerda representam “andar” paralelo a qual eixo? No sentido positivo ou negativo?
Retomada

Tempo sugerido: 8 minutos. (slides 3, 4,5 e 6 ).
Orientações:
Observe se cada rodada está sendo representada em um plano cartesiano específico, do contrário, oriente os alunos a representarem dessa forma.
Propósito: Rever conceitos relacionados a localização de um ponto no plano cartesiano, bem como localizar pontos a partir de um ponto dado, através de “deslocamentos” horizontais e verticais.
Discuta com a turma:
- Deslocamentos para baixo representam “andar” paralelo a qual eixo? No sentido positivo ou negativo?
- Deslocamentos para a direita representam “andar” paralelo a qual eixo? No sentido positivo ou negativo?
Atividade Principal

Tempo sugerido: 20 minutos. (slides 7, 8, 9, 10, 11 e 12).
Orientações:
Descreva de forma clara e objetiva as regras do jogo.
Propósito: Aplicar o Teorema de Pitágoras para determinar a distância entre dois pontos no plano cartesiano.
Discuta com a turma:
- Qual a menor distância entre dois pontos no plano?
Materiais complementares para impressão:
Atividade Principal

Tempo sugerido: 20 minutos. (slides 7, 8, 9, 10, 11 e 12).
Orientações: Descreva a distribuição dos pontos de acordo com os objetivos do jogo. Se necessário exemplifique, simulando uma rodada.
Propósito: Aplicar o Teorema de Pitágoras para determinar a distância entre dois pontos no plano cartesiano.
Discuta com a turma:
- Em um ponto P(a,b) quem é a abscissa? Quem é a ordenada?
Atividade Principal
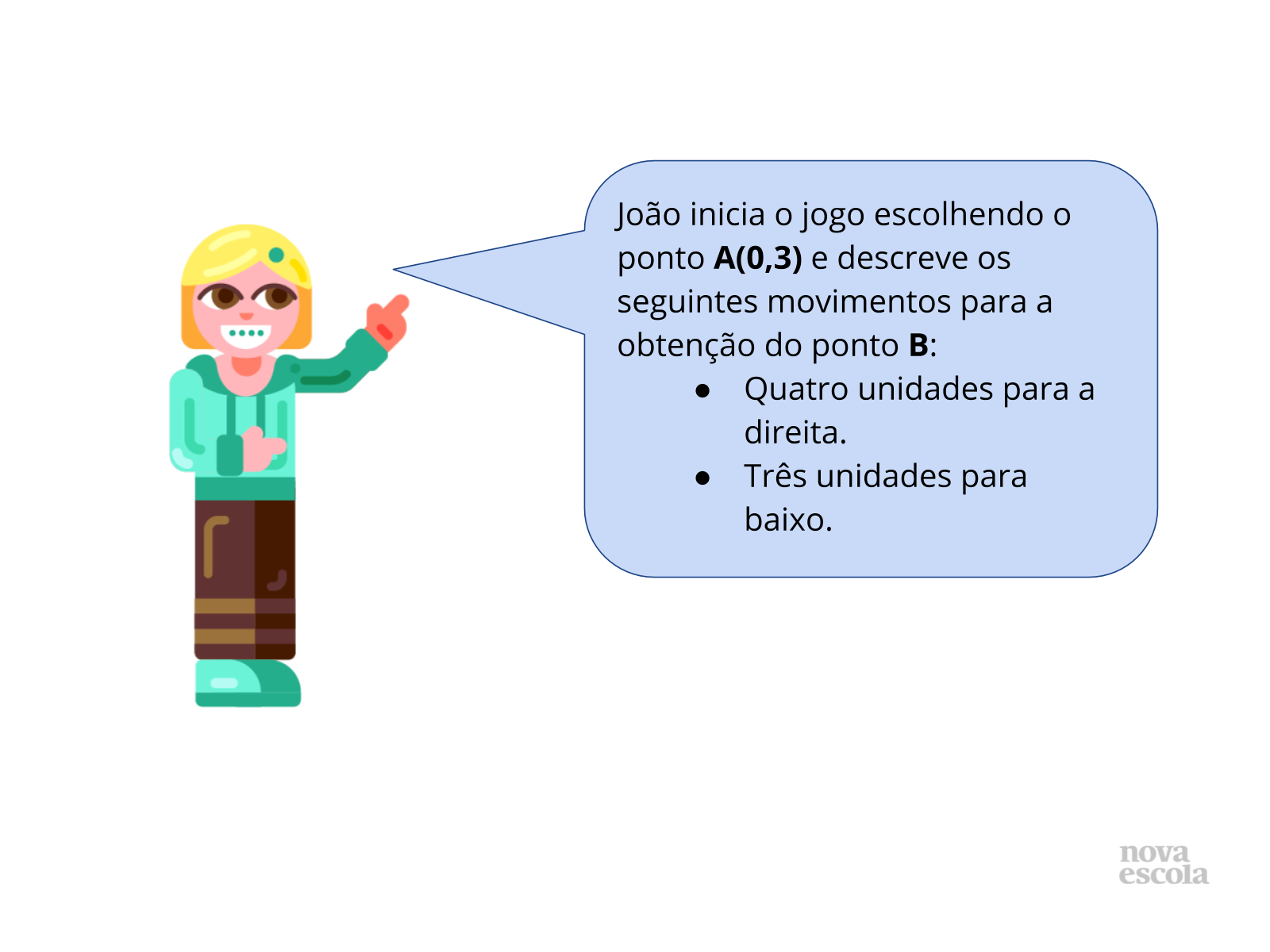
Tempo sugerido: 20 minutos. (slides 7, 8, 9, 10, 11 e 12).
Orientações:
Disponibilize papel com malhas quadriculadas para que desenvolvam a atividade. Oriente o uso de régua e lápis para traçar os eixos coordenados e os “deslocamentos” no plano.
Propósito: Aplicar o Teorema de Pitágoras para determinar a distância entre dois pontos no plano cartesiano.
Discuta com a turma:
- Um ponto da forma P(0,y), com y diferente de 0(zero), se localiza em algum quadrante? Por quê?
- Um ponto da forma P(x,0), com x diferente de 0(zero), se localiza em algum quadrante? Por quê?
- Um ponto da forma P(x,y), com x e y diferentes de 0(zero), se localiza em algum quadrante? Por quê?
Atividade Principal

Tempo sugerido: 20 minutos. (slides 7, 8, 9, 10, 11 e 12).
Orientações: Disponibilize papel com malhas quadriculadas para que desenvolvam a atividade. Oriente o uso de régua e lápis para traçar os eixos coordenados e os “deslocamentos” no plano.
Propósito: Aplicar o Teorema de Pitágoras para determinar a distância entre dois pontos no plano cartesiano.
Discuta com a turma:
- Qual a relação entre a medida de uma lado de um triângulo e a soma das medidas dos outros dois lados: maior, menor ou igual?
- Qual a intersecção de dois segmentos de reta perpendiculares?
- Qual a coordenada do ponto P, intersecção dos segmentos que representam os deslocamentos?
- Qual a condição necessária para que 3 pontos formem os vértices de um triângulo?
Atividade Principal

Tempo sugerido: 20 minutos. (slides 7, 8, 9, 10, 11 e 12).
Orientações:
Disponibilize papel com malhas quadriculadas para que desenvolvam a atividade. Oriente o uso de régua e lápis para traçar os eixos coordenados e os “deslocamentos” no plano.
Propósito: Aplicar o Teorema de Pitágoras para determinar a distância entre dois pontos no plano cartesiano.
Discuta com a turma:
- Deslocar para a esquerda na horizontal, significa ir em que sentido paralelo ao eixo 0x?
- Deslocar para a cima na vertical, significa ir em que sentido paralelo ao eixo 0y?
- Pode haver um deslocamento nulo? O que isso significa?
Atividade Principal

Tempo sugerido: 20 minutos. (slides 7, 8, 9, 10, 11 e 12).
Orientações:
Disponibilize papel com malhas quadriculadas para que desenvolvam a atividade. Oriente o uso de régua e lápis para traçar os eixos coordenados e os “deslocamentos” no plano.
Propósito: Aplicar o Teorema de Pitágoras para determinar a distância entre dois pontos no plano cartesiano.
Discuta com a turma:
- Pelas medidas dos deslocamentos (catetos), qual sua estimativa para a distância entre os pontos A e B ?
Atividade Principal

Tempo sugerido: 8 minutos.
Orientações: Estimule os alunos a socializarem suas hipóteses e dificuldades na representação e na determinação da distância entre dois pontos no plano. Devido o tempo reduzido, optou-se em usar um modelo genérico (Triângulo) para realizar a discussão, o que certamente contribui para que o aluno possa internalizar os conceitos desenvolvidos de forma mais abrangente e significativa.
Propósito: Discutir a solução e as dificuldades apresentadas no decorrer da atividade.
Discuta com a turma:
- O método desenvolvido para determinar a distância entre dois pontos no plano, apresenta alguma limitação?
- É possível aplicar tal método quando os pontos estiverem alinhados na vertical ou horizontal?
- Qual o procedimento quando os pontos estiverem alinhados na vertical ou horizontal?
Encerramento

Tempo sugerido: 5 minutos.
Orientações: Encerre a aula resumindo com os alunos o conceito desenvolvido.
Propósito: Sintetizar o que foi desenvolvido na aula.
Discuta com a turma:
- Caso os pontos estejam alinhados, na horizontal ou vertical, tal procedimento é possível?
- Como determinar a distância entre os dois pontos neste caso?
Raio X
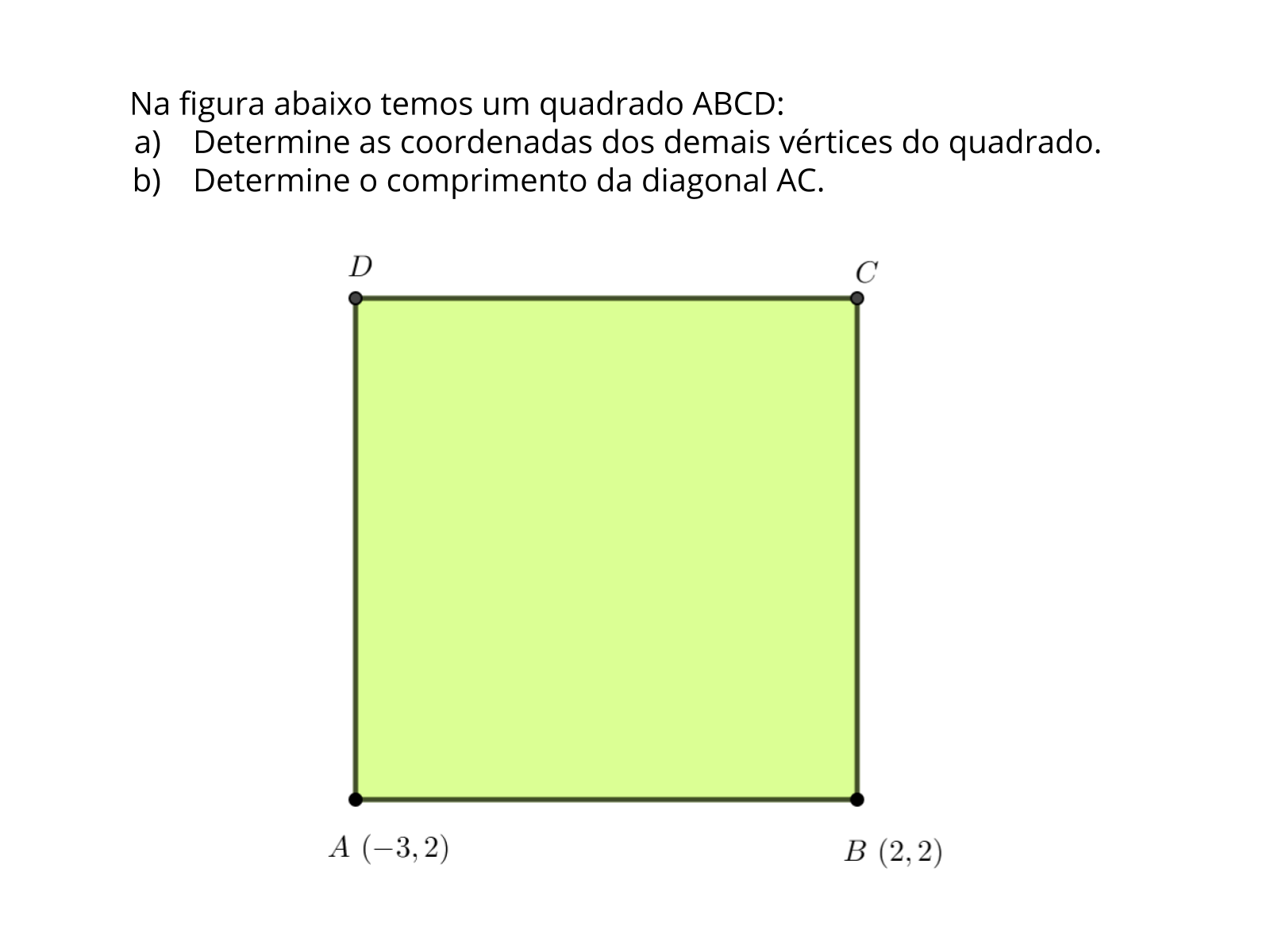
Tempo sugerido: 5 minutos.
Orientações:
Observe que a atividade não foi construída em malha quadriculada, o que requer mais atenção na resolução por parte do aluno, em relação a determinar as coordenadas dos pontos C e D.
Propósito: Avaliar se os objetivos da aula foram alcançados
Discussão com a turma:
- O que tem em comum 2 pontos sobre a mesma reta horizontal?
- O que tem em comum 2 pontos sobre a mesma reta vertical ?
- Como determinar a distância entre dois pontos quando os mesmos estiverem sobre uma mesma reta horizontal/vertical?
- Como determinar a distância entre dois pontos quando os mesmos não estiverem sobre uma mesma reta horizontal/vertical?
Materiais complementares para impressão:
Sugestão de adaptação para ensino remoto
Código do plano (MAT9_15GEO05)
Ferramentas sugeridas
- Essenciais: Alguma rede social (Whatsapp, Facebook, etc.) régua e papel para anotações.
- Optativas: Calculadora e tesoura.
Aquecimento
- Pela rede social escolhida, inicie esse contato questionando se seus alunos e alunas lembram das posições dos pontos no plano cartesiano. Nesse aquecimento, faça perguntas usando coordenadas e sobre o que significa a posição x e a posição y nos pontos (x , y).
Atividade principal
Como atividade principal, em substituição ao jogo proposto no plano original, sugerimos que solicite aos seus alunos e alunas acessarem ao link:
https://pt.khanacademy.org/math/basic-geo/basic-geometry-pythagorean-theorem#pythagorean-theorem-distance
Lá poderão assistir a um vídeo explicativo, após isso determine que realizem o máximo de exercícios possíveis daquele módulo, combinando um tempo para o retorno do contato e discussão das soluções e dúvidas existentes.
Discussão das soluções, sistematização e encerramento
Reforce o fato de que é sempre possível determinar a distância entre dois pontos, pois basta modelar a situação para um triângulo retângulo e aplicar o teorema de Pitágoras.
Raio X
Use a atividade do próprio plano, mas descrevendo a situação para quem não conseguir visualizar a imagem.
Convite às famílias
Peça para que seus alunos envolvam seus familiares, próximos neste momento, e relatem suas explorações sobre os exercícios do link acessado.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Sebastiao Rodrigues da Silva
Mentor: Lara Martins Barbosa
Especialista de área: Pricilla Mendes Cerqueira
Habilidade da BNCC
(EF09MA14) Resolver e elaborar problemas de aplicação do teorema de Pitágoras ou das relações de proporcionalidade envolvendo retas paralelas cortadas por secantes.
Objetivos específicos
Aplicar o teorema de Pitágoras para determinar a distância entre dois pontos no plano cartesiano.
Conceito-chave
Utilização do Teorema de Pitágoras como conceito auxiliar no cálculo de distâncias entre pontos no plano cartesiano
Recursos necessários
- Lápis, régua.
- Malha quadriculada
- Atividades impressas.