Objetivo
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Cátia do Vale dos Santos Mendes
Mentora: Sônia Maria dos Santos Campos Neves
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF05MA02 - Ler, escrever e ordenar números racionais na forma decimal com compreensão das principais características do sistema de numeração decimal, utilizando, como recursos, a composição e decomposição e a reta numérica.
EF05MA03 - Identificar e representar frações (menores e maiores que a unidade), associando-as ao resultado de uma divisão ou à ideia de parte de um todo, utilizando a reta numérica como recurso.
Objetivos específicos
Identificar a representação fracionária e decimal de quantidades maiores e menores que a unidade.
Reconhecer a relação entre frações e números decimais.
Conhecimentos prévios
Representação fracionária e decimal de quantidades maiores e menores que a unidade;
Conceito-chave
Representação fracionária e decimal de quantidades maiores e menores que a unidade.
Recursos necessários
Cadernos, atividade impressa, material dourado, quadro, pincel ou giz coloridos, lápis de cor, lápis de escrever, réguas e borrachas.
Objetivo
- Tempo sugerido: 2 minutos
- Orientação: Apenas leia o objetivo para a turma, ressaltando a importância da colaboração dos alunos para atingir as metas estabelecidas para a aula.
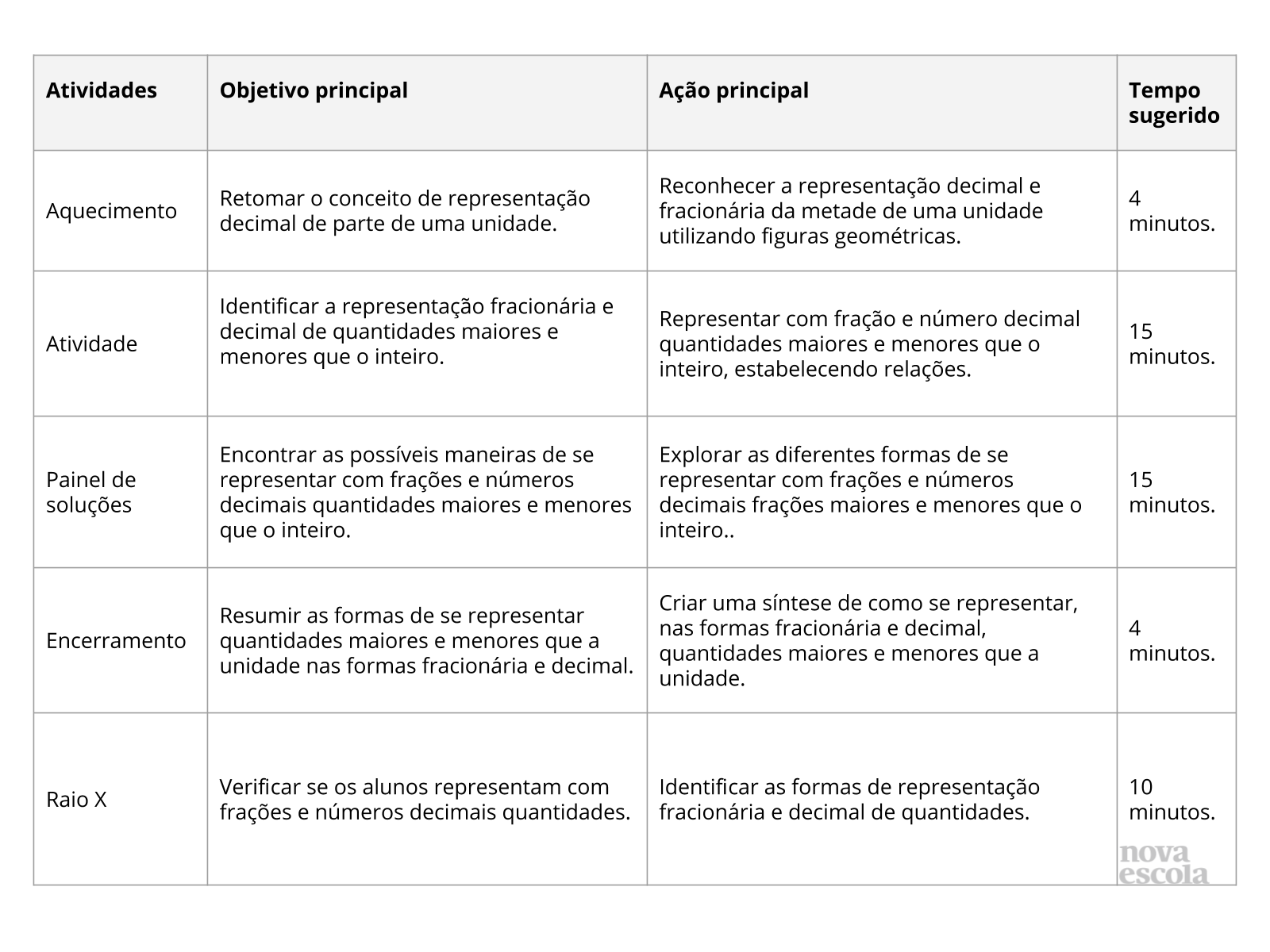
Aquecimento
AquecimentoTempo sugerido: 4 minutos
Orientação: Inicie a atividade lembrando ao aluno que todo número decimal é provém de uma representação fracionária de algo, que pode ser uma figura geométrica ou uma quantidade.
Propósito: Retomar o conceito de representação decimal e fracionária de figuras geométricas.
Discuta com a turma:
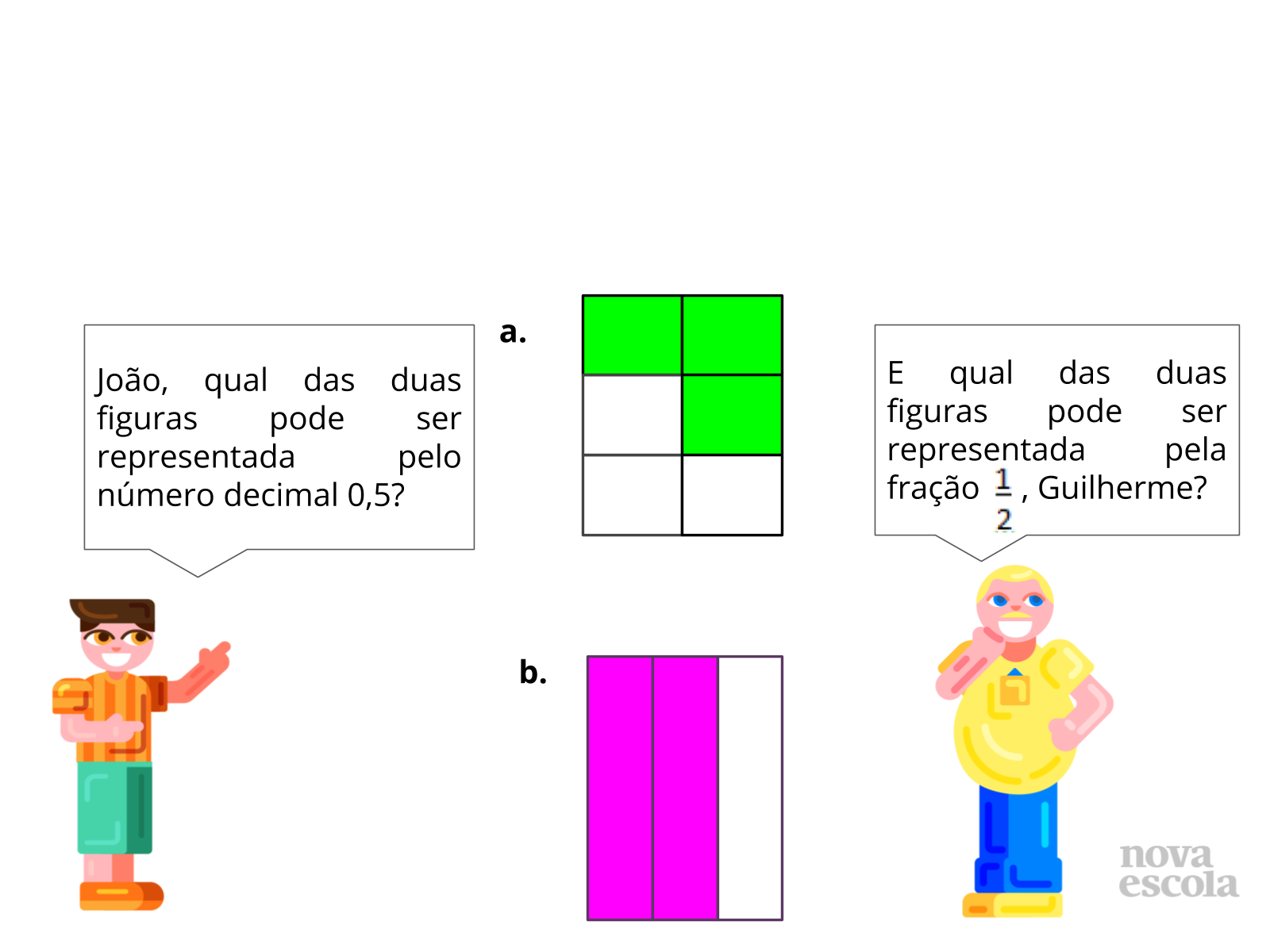
- Quantas partes tem a figura a? E a figura b?
- Quantas partes estão coloridas na figura a? E na figura b?
- O que representa o número decimal 0,5? Ele pode ser representado por qual fração?
- Qual das duas figuras pode representar o número 0,5? E ½?
Atividade principal 1
Atividade principal 1Tempo sugerido: 15 minutos (Slides 4 e 5)
Orientação: Antes de iniciar a atividade, relembre aos alunos que eles possuem diferentes formas de representar partes de uma unidade, podendo ser frações ou números decimais, uma vez que toda fração tem uma representação decimal ou vice-versa. Deixe que as crianças, em dupla, explorem as possibilidades de resolução desta atividade.
Propósito: Identificar a representação fracionária e decimal de partes menores que a unidade.
Discuta com a turma:
- Em quantas partes o chocolate está dividido?
- Quantas partes do chocolate foram comidas? Quantas sobraram?
- Que fração posso utilizar para representar a parte comida? Por quê?
- Que número decimal posso utilizar para representar a parte que sobrou? Por quê?
- Que fração posso utilizar para representar a parte que sobrou? Que número decimal representa esta fração?
Materiais Complementares:
Atividade principal 2
Atividade principal 2Tempo sugerido: 15 minutos (Slides 4 e 5)
Orientação: Lembre aos alunos que toda fração corresponde a uma divisão de unidades em partes e possui, também, uma representação decimal. Neste caso, tenho três chocolates para dividir entre duas crianças, ou seja, 3:2 que corresponde a 3/2. Assim, temos uma fração maior que o inteiro, que possui outras formas de representação: uma mista e uma decimal. Deixe que as crianças, em dupla, explorem as possibilidades de resolução desta atividade.
Propósito: Identificar a representação fracionária e decimal de partes maiores que a unidade.
Discuta com a turma:
- Quantos chocolates a menina precisa dividir?
- Os chocolates serão divididos entre quantas crianças?
- Considerando que o numerador corresponde às partes utilizadas e o denominador às partes em que será dividido o chocolate, que fração representa os chocolates e as partes em que serão divididos?
- Podemos afirmar que toda fração é uma divisão? Por quê?
Materiais Complementares:
Discussão da solução 1
Discussão da solução 1Tempo sugerido: 15 minutos (slides 6 a 9)
Orientação: Deixe que os alunos percebam que não existe apenas uma maneira de resolver essa questão, podendo utilizar tanto números fracionários quanto decimais. É importante que compreendam que toda fração possui uma representação decimal e vice-versa.
Propósito: Explorar as diferentes formas de se representar quantidades menores que a unidade.
Discuta com a turma:
- Em quantas partes o chocolate está dividido?
- Quantas partes do chocolate foram consumidas?
- Que fração pode representar a quantidade consumida?
- Qual número decimal representa a parte consumida?
- Para que serve a vírgula nos números decimais? O que representam os décimos?
- Por que não há nenhum número à esquerda da vírgula?
Materiais complementares:
Discussão da solução 1
Discussão da solução 1Tempo sugerido: 15 minutos (slides 6 a 9)
Orientação: Deixe que os alunos percebam que não existe apenas uma maneira de resolver essa questão, podendo utilizar tanto números fracionários quanto decimais. É importante que compreendam que toda fração possui uma representação decimal e vice-versa.
Propósito: Explorar as diferentes formas de se representar quantidades menores que a unidade.
Discuta com a turma:
- Em quantas partes o chocolate está dividido?
- Quantas partes do chocolate sobraram?
- Que fração pode representar a quantidade que sobrou?
- Qual número decimal representa a parte que sobrou?
- Por que não há nenhum número à esquerda da vírgula?
Materiais complementares:
Discussão da solução 2
Discussão da solução 2Tempo sugerido: 15 minutos (slides 6 a 9)
Orientação: Deixe espaço para que as duplas discutam as diferentes maneiras de se resolver esta questão. Assim, verão que podem chegar a uma fração ou a um número decimal maior que a unidade.
Propósito: Explorar as diferentes formas de se representar quantidades maiores que a unidade.
Discuta com a turma:
- A questão apresenta quantos chocolates? Eles precisam ser dividido entre quantas pessoas?
- Como você pode realizar a divisão dos chocolates?
- Cada criança receberá mais ou menos de um chocolate inteiro? Por quê?
- Que fração representa a quantidade de chocolate que cada menina receberá?
Materiais complementares:
Discussão da solução 2
Discussão da solução 2Tempo sugerido: 15 minutos (slides 6 a 9)
Orientação: Lembre aos alunos que as frações maiores que o inteiro podem ser representadas por números mistos e que, nos números decimais, colocamos as unidades antes da vírgula, uma vez que a atividade sugere uma fração maior que a unidade. Ressalte que toda fração tem uma representação decimal e vice-versa.
Propósito: Explorar as diferentes formas de se representar quantidades maiores que a unidade.
Discuta com a turma:
- Quantos chocolates precisam ser divididos entre as meninas?
- Quantos chocolates inteiros cada uma receberá?
- O que pode ser feito com o chocolate que sobrou?
- Que número misto pode ser formado com o chocolate inteiro e a parte do outro chocolate que cada menina recebeu?
- Que número decimal representa a fração ½?
- Que número decimal pode ser formado com esse número misto?
- Por que antes da vírgula não permaneceu o número 0?
Materiais complementares:
Encerramento
EncerramentoTempo sugerido: 4 minutos.
Orientação: Oriente os alunos a se lembrar do que foi trabalhado na atividade principal e relatarem, e poucas palavras, a que conclusão chegaram ao resolvê-la. Lembre a eles da quantidade partes em que o chocolate foi dividido em cada situação. Vá registrando no quadro as opiniões principais que os alunos emitiram e, no final, forme um parágrafo evidenciando os conhecimentos privilegiados da aula.
Propósito: Resumir as formas de se representar quantidades maiores e menores que a unidade nas formas fracionária e decimal.
Discuta com a turma:
- Que frações foram abordadas na atividade principal? De que outra forma elas foram representadas?
- Que conclusão podemos tirar ao analisar as formas de representação utilizadas na atividade principal?
Raio X_MAT5_NUM09
Raio X_MAT5_NUM09Tempo sugerido: 10 minutos.
Orientação: Organize os alunos em duplas. Peça que cada um faça a sua atividade e, depois, compare a resposta com a do colega ao lado. Lembre aos alunos que toda fração tem uma representação decimal.
Propósito: Verificar se os alunos identificam a representação fracionária e decimal de uma quantidade.
Discuta com a turma:
- Quantas maçãs Carolina comprou?
- Com quantas maçãs inteiras cada menina ficará?
- Alguma maçã precisará ser repartida? Em quantos pedaços?
- Que fração representa a quantidade que cada menina recebeu? Que número decimal representa esta fração?
Materiais complementares:
