Aquecimento
Plano de Aula
Plano de aula: Diferença de quadrados
Plano 3 de uma sequência de 10 planos. Veja todos os planos sobre Expressões algébricas e fatoração
Descrição
Autor: Flávia Aparecida Britto
Mentor: Telma Regina França Rosso
Especialista de área: Sandra Amorim
Habilidade da BNCC
EF09MA09: Compreender os processos de fatoração de expressões algébricas, com base em suas relações com os produtos notáveis, para resolver e elaborar problemas que possam ser representados por equações polinomiais do 2º grau.
Objetivos específicos
Entender que as expressões (x - a).(x+a) e x² + 2ax +a² são equivalentes.
Fatorar expressões do tipo x² -a².
Conceito-chave
Fatoração de expressões algébricas
Recursos necessários
- Projetor para apresentação dos slides da aula;
- Atividades impressas em folhas, coladas no caderno ou não.
Habilidades BNCC:
Objetivos de aprendizagem
Entender que as expressões (x - a).(x+a) e x² + 2ax +a² são equivalentes.
Fatorar expressões do tipo x² -a².
Resumo da aula
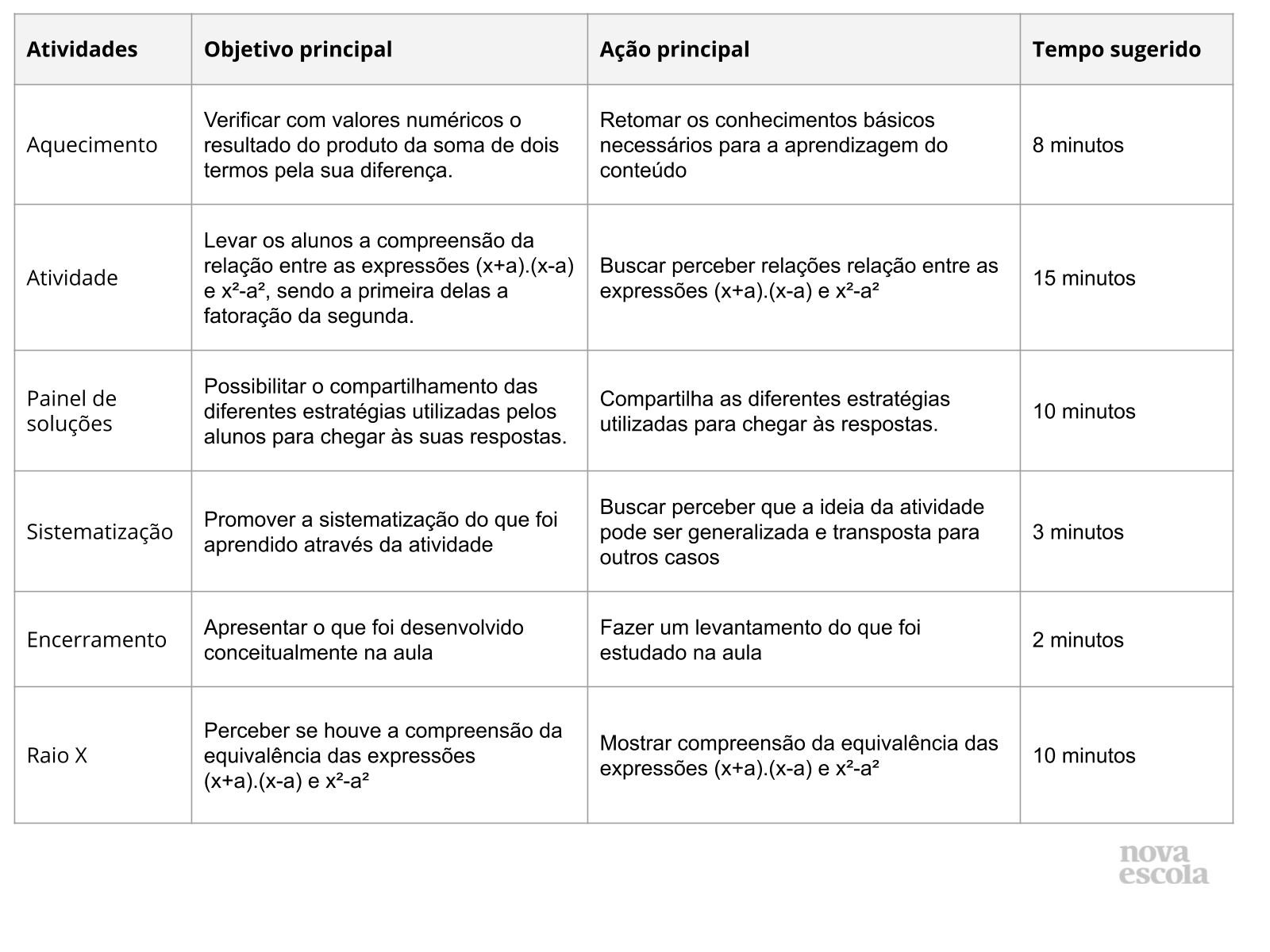 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Leitura individual ou leitura compartilhada junto com os estudantes para deixar claro o objetivo da aula.
Propósito: Compartilhar o objetivo da aula com os alunos

Título: Aquecimento
Tempo sugerido: 8 minutos
Orientação: Professor, a ideia é que o aluno use alguns valores numéricos para perceber o que ocorre quando multiplicamos uma soma de fatores por uma diferença dos mesmos fatores. Na atividade principal ele irá trabalhar com expressões algébricas semelhantes.
O resultado de 6.6=6² = 36, ao fazermos 8.4, somamos uma unidade ao primeiro fator e subtraímos uma unidade do outro, ou seja, fizemos (6+2).(6-2) = 6² -4, ou seja o resultado é quatro unidades menor (na verdade 2²). Se tivéssemos acrescentado 3 unidades em um fator e subtraído 3 no outro fator, o resultado seria 9 unidades menor (ou 3²). Assim, generalizando para teríamos 6² - a² como resultado quando acrescentamos a unidades em um fator e subtraímos a unidades ao outro, com 0 Propósito: Introduzir a noção de do produto da soma de dois termos pela diferença dos mesmos termos usando, inicialmente, valores numéricos. Discuta com a turma: Materiais complementares:
Atividade principal
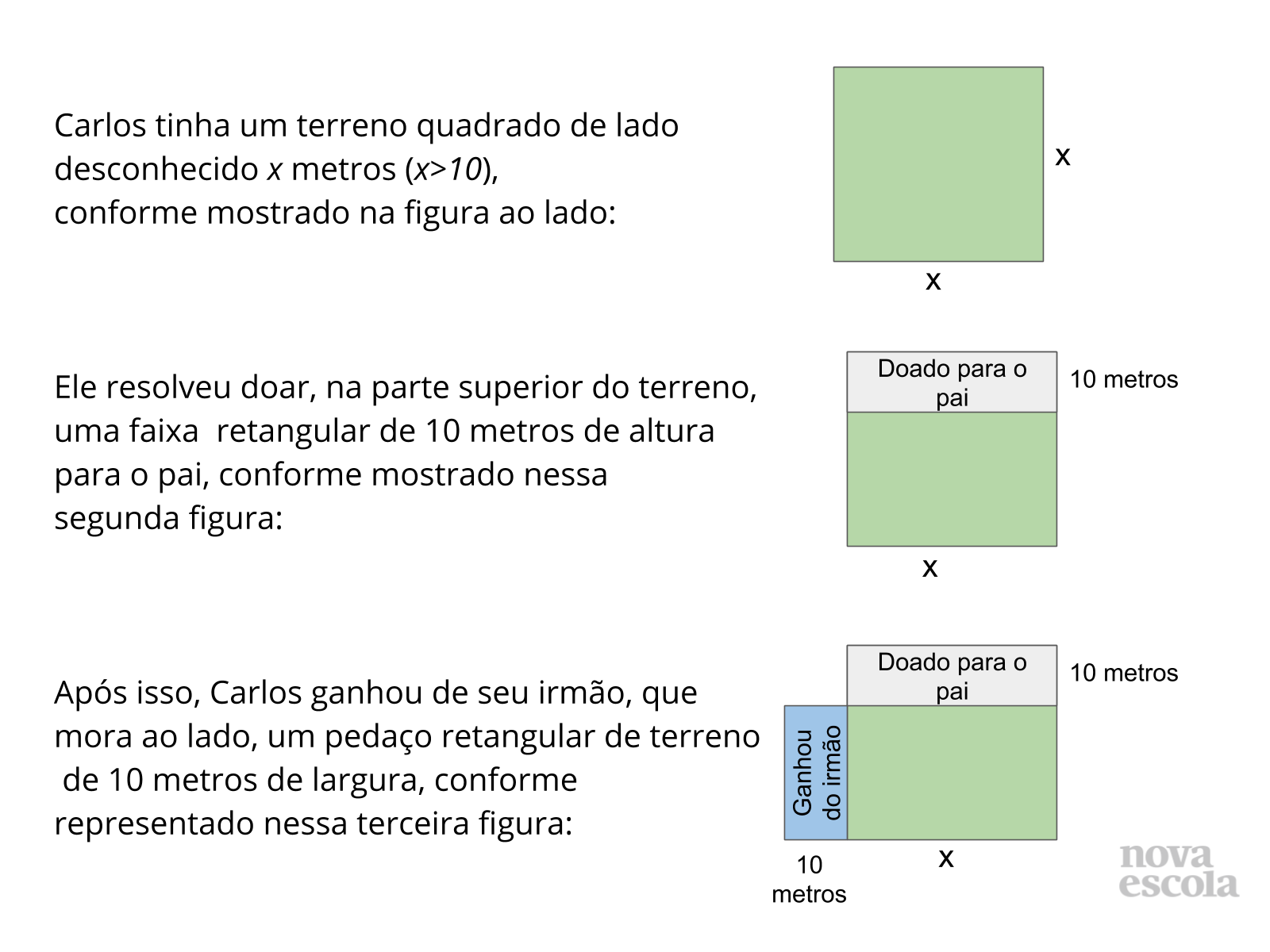
Tempo sugerido: 15 minutos. (Slide 4 e 5)
Orientações:: Você poderá projetar o problema no quadro, ou entregá-lo impresso aos seus alunos. Os alunos poderão resolver a atividade individualmente, ou em duplas. Caso opte pelo trabalho individual, não se esqueça de pedir para que compartilhem no momento de discussão das soluções as diferentes estratégias usadas para a resolução da atividade. Se optar pelo desenvolvimento da atividade em dupla, peçam para que primeiro cada um pense em estratégias para encontrar as respostas e depois compartilhem com o colega, explicando como pensaram. As justificativas são muito importantes.
Propósito: Apresentar o contexto da atividade principal para os alunos.
Discuta com a turma:
- Como chegou(ram) a essa solução?
- Por quê essa expressão atende ao que está sendo pedido?
- Há outras possibilidades de resposta? Quais? Consulte a discussão das soluções, para verificar algumas possibilidades de respostas.
Atividade principal

Tempo sugerido: 15 minutos. (Slide 4 e 5)
Orientações:: Você poderá projetar o problema no quadro, ou entregá-lo impresso aos seus alunos. Os alunos poderão resolver a atividade individualmente, ou em duplas. Caso opte pelo trabalho individual, não se esqueça de pedir para que compartilhem no momento de discussão das soluções as diferentes estratégias usadas para a resolução da atividade. Se optar pelo desenvolvimento da atividade em dupla, peçam para que primeiro cada um pense em estratégias para encontrar as respostas e depois compartilhem com o colega, explicando como pensaram. As justificativas são muito importantes.
Propósito: Apresentar o contexto da atividade principal para os alunos.
Discuta com a turma:
- Como chegou(ram) a essa solução?
- Por quê essa expressão atende ao que está sendo pedido?
- Há outras possibilidades de resposta? Quais? Consulte a discussão das soluções, para verificar algumas possibilidades de respostas.
Materiais Complementares:
Discussão das soluções

Tempo sugerido: 10 minutos. (Slides 6 a 8)
Orientações: Reserve esse momento para que alguns de seus alunos expliquem como chegaram às respostas de cada item da atividade. Você pode fazer o convite a alguns deles ou perguntar quem gostaria de mostrar como pensou. Lembre-se de que mesmo aqueles que não chegaram à respostas corretas tiveram um raciocínio no processo de solução e podem trazer muitas contribuições apresentando-o à turma para que investiguem juntos por que o erro ocorreu e como ele poderia ser evitado.
No slide 7, sugerimos uma primeira possibilidade de resolução do problema em que a região do terreno de Carlos é percebida como um retângulo cujas dimensões são (x+10) e (x-10).
Já no slide 8, apresentamos uma segunda possibilidade de solução do problema em que o terreno de Carlos é percebido como sendo composto por dois retângulos e, após o cálculo de suas respectivas áreas, elas são somadas.
Propósito: Levantar as estratégias que os alunos usaram para resolver a atividade principal.
Discuta com a turma:
- Pergunte a cada aluno: Como você pensou para chegar a essa resposta?
- Pergunte à turma: Quais outras estratégias poderíamos usar?
- Pergunte aos seus alunos se encontraram soluções distintas.
Discussão das soluções
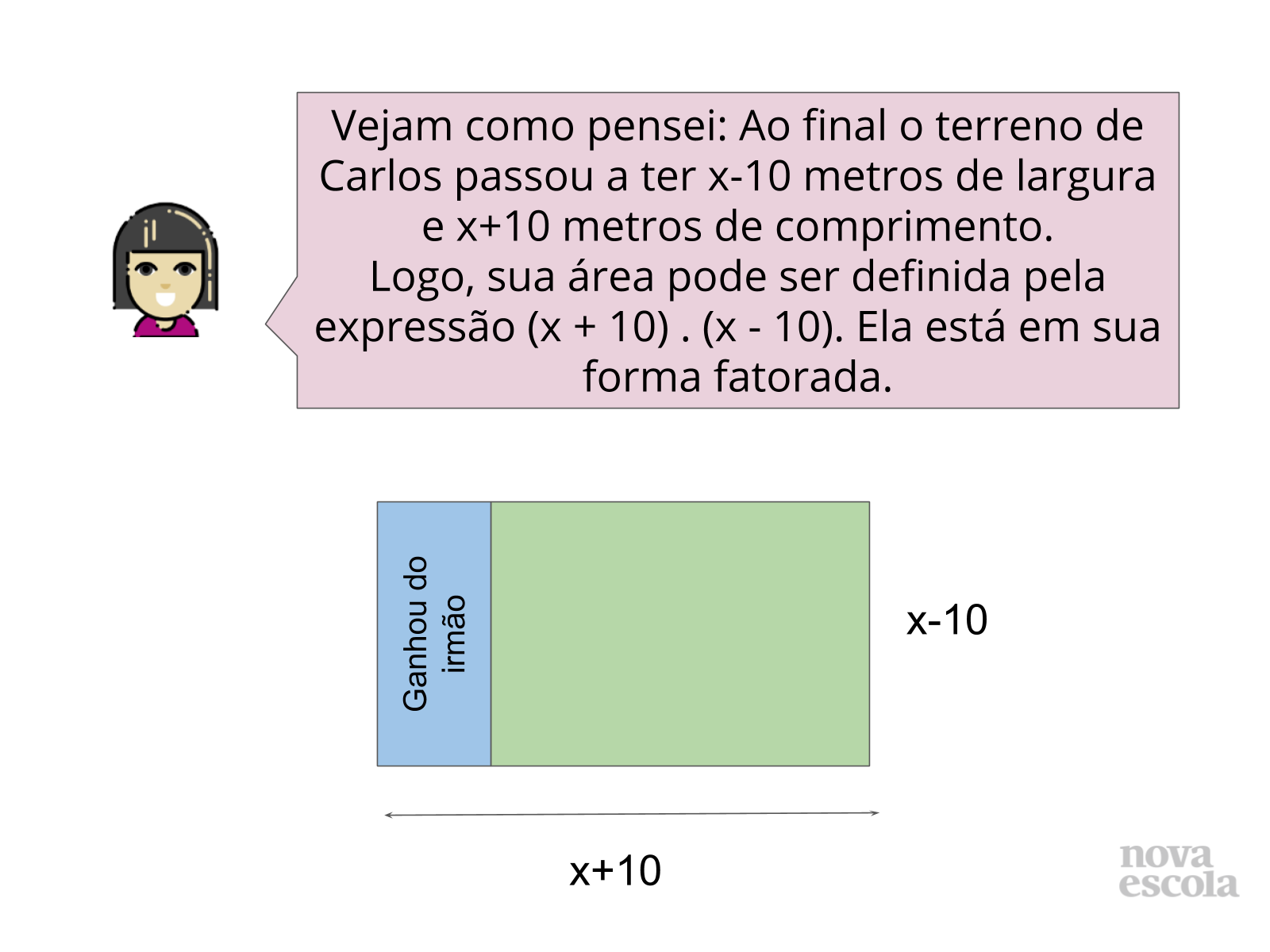
Tempo sugerido: 10 minutos. (Slides 6 a 8)
Orientações: Reserve esse momento para que alguns de seus alunos expliquem como chegaram às respostas de cada item da atividade. Você pode fazer o convite a alguns deles ou perguntar quem gostaria de mostrar como pensou. Lembre-se de que mesmo aqueles que não chegaram à respostas corretas tiveram um raciocínio no processo de solução e podem trazer muitas contribuições apresentando-o à turma para que investiguem juntos por que o erro ocorreu e como ele poderia ser evitado.
No slide 7, sugerimos uma primeira possibilidade de resolução do problema em que a região do terreno de Carlos é percebida como um retângulo cujas dimensões são (x+10) e (x-10).
Já no slide 8, apresentamos uma segunda possibilidade de solução do problema em que o terreno de Carlos é percebido como sendo composto por dois retângulos e, após o cálculo de suas respectivas áreas, elas são somadas.
Propósito: Levantar as estratégias que os alunos usaram para resolver a atividade principal.
Discuta com a turma:
- Pergunte a cada aluno: Como você pensou para chegar a essa resposta?
- Pergunte à turma: Quais outras estratégias poderíamos usar?
- Pergunte aos seus alunos se encontraram soluções distintas.
Discussão das soluções

Tempo sugerido: 10 minutos. (Slides 6 a 8)
Orientações: Reserve esse momento para que alguns de seus alunos expliquem como chegaram às respostas de cada item da atividade. Você pode fazer o convite a alguns deles ou perguntar quem gostaria de mostrar como pensou. Lembre-se de que mesmo aqueles que não chegaram à respostas corretas tiveram um raciocínio no processo de solução e podem trazer muitas contribuições apresentando-o à turma para que investiguem juntos por que o erro ocorreu e como ele poderia ser evitado.
No slide 7, sugerimos uma primeira possibilidade de resolução do problema em que a região do terreno de Carlos é percebida como um retângulo cujas dimensões são (x+10) e (x-10).
Já no slide 8, apresentamos uma segunda possibilidade de solução do problema em que o terreno de Carlos é percebido como sendo composto por dois retângulos e, após o cálculo de suas respectivas áreas, elas são somadas.
Propósito: Levantar as estratégias que os alunos usaram para resolver a atividade principal.
Discuta com a turma:
- Pergunte a cada aluno: Como você pensou para chegar a essa resposta?
- Pergunte à turma: Quais outras estratégias poderíamos usar?
- Pergunte aos seus alunos se encontraram soluções distintas.
Sistematização do conceito

Tempo sugerido: 3 minutos
Orientação: Aqui é apresentada uma sistematização para os resultados encontrados. Comente com os alunos que as diversas estratégias usadas para descobrir a área do terreno de Carlos são equivalentes. Dessa forma, podemos dizer que x²-100 = (x+10).(x-10).
Certifique-se de que os alunos entendem que a expressão x²-100 é equivalente a sua forma fatorada (x+10).(x-10).
No slide 10, realizamos a generalização do raciocínio desenvolvido na atividade principal. Você pode usar a propriedade distributiva da multiplicação na expressão (x+a).(x-a) para demonstrar aos alunos que ela é equivalente à x²-a², mas é possível também usar o raciocínio das áreas, de modo semelhante ao que foi mostrado na discussão das soluções (slides 7 e 8).
Propósito: Promover uma sistematização dos conceitos e ideias centrais focalizadas na atividade principal
Sistematização do conceito
Tempo sugerido: 3 minutos
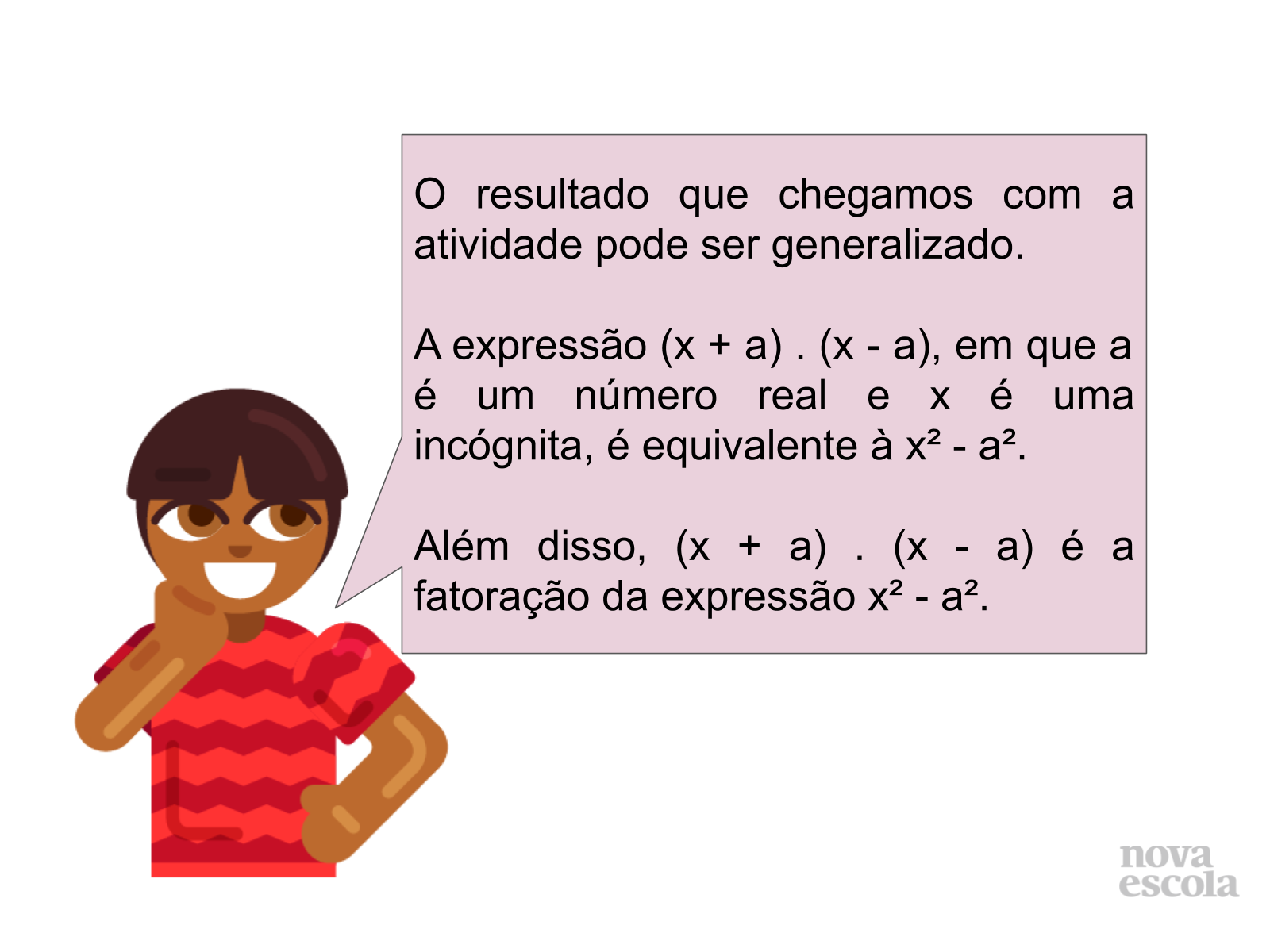
Orientação: Aqui é apresentada uma sistematização para os resultados encontrados. Comente com os alunos que as diversas estratégias usadas para descobrir a área do terreno de Carlos são equivalentes. Dessa forma, podemos dizer que x²-100 = (x+10).(x-10).
Certifique-se de que os alunos entendem que a expressão x²-100 é equivalente a sua forma fatorada (x+10).(x-10).
No slide 10, realizamos a generalização do raciocínio desenvolvido na atividade principal. Você pode usar a propriedade distributiva da multiplicação na expressão (x+a).(x-a) para demonstrar aos alunos que ela é equivalente à x²-a², mas é possível também usar o raciocínio das áreas, de modo semelhante ao que foi mostrado na discussão das soluções (slides 7 e 8).
Propósito: Promover uma sistematização dos conceitos e ideias centrais focalizadas na atividade principal
Encerramento

Tempo sugerido: 2 minutos
Orientação: Encerre a aula explicitando aos alunos o que foi aprendido na aula. Certifique-se de todas as informações ficaram claras.
Propósito: Encerrar a aula com um resumo dos conceitos e ideias centrais focalizadas na atividade principal
Materiais complementares:
Você encontrará sugestões de mais atividades sobre o assunto nessa apostila elaborada pela Coordenadoria de Educação do Rio de Janeiro - clique aqui
Raio x

Tempo sugerido: 10 minutos
Orientação: Leia atentamente a atividade junto dos alunos e depois solicite que todos a resolvam individualmente.
A expressão encontrada pelo aluno para resolver o problema estará associada a uma diferença de quadrados (x²-9), que possui por fatoração (x+3).(x-3). O aluno poderá obter outras expressões equivalentes a essas a partir da partição da figura em outras menores.
Propósito: Verificar se os conceitos discutidos na aula foram aprendidos pelos alunos.
Discuta com a turma:
- Existem outras expressões equivalentes que definem a área verde depois da construção da piscina?
Materiais Complementares:
Sugestão de adaptação para ensino remoto
Código do plano (MAT9_05ALG03)
Ferramentas sugeridas
- Essenciais: Alguma rede social (Whatsapp, Facebook, etc.) e papel para anotações, régua.
- Optativas: Calculadora e tesoura.
Aquecimento
- Pela rede social escolhida, questione sobre a fatoração algébrica gerada por expressões do tipo: (a + b)² = a² + 2. a.b + b². E reforce que é chamado de um produto notável.
Atividade principal
Proponha para os alunos refazerem as tarefas de dobrar e recortar a folha, mas com algumas modificações, nessa ordem:
1) Faça uma dobra e corte a folha conforme a imagem abaixo (A4, do caderno...):

2) Depois de cortar, chame o lado do quadrado pela letra a e o lado menor do retângulo cortado de b. Anote o comprimento dos lados usando a e b para escrever.
3) Agora, nesse retângulo, refaça a mesma dobra que realizou na folha inteira e recorte o quadradinho dele, ficando, assim, com um retângulo menor.
4) No primeiro quadrado, faça a dobra de um retângulo com a medida b e recorte-o, ficando, assim, não mais com um quadrado, mas com um retângulo maior.
5) Sabendo que os lados iniciais do quadrado eram L1 = a e do retângulo L1 = a e L2 = a + b, escreva a medida dos lados do retângulo que resultou do quadrado e do retângulo no qual foi retirado o quadradinho.
6) Nesse momento, junte esses retângulos do item 5) e escreva a expressão para a área resultante dessa união.
Painel de soluções
1) Depende da folha.
2) Assim, os lados do retângulo ficarão: L1 = a e L2 = b. E do quadrado: L1 = a.
3) Assim, os lados do retângulo inicial ficarão: L3 = a - b e L2 = b.
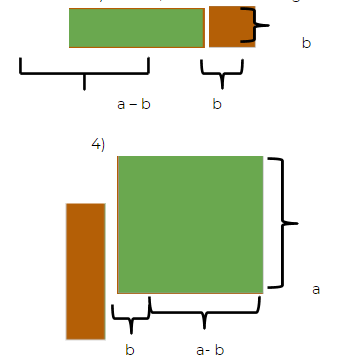
5) Do retângulo maior, temos: L1 = a - b e L2 = a. E do retângulo menor, temos: L3 = a - b e L4 = b
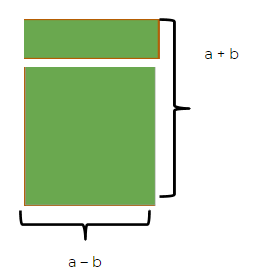
Daí, temos: A = (a+b).(a-b)
Discussão das soluções
Aplicando a distributiva (ou, simplesmente, lembrando dos produtos notáveis), resolva a expressão: (a + b).(a - b) = a² - b²
Sistematização e encerramento
- Faça uma sistematização dizendo que escrever qualquer expressão algébrica a² - b² , é gerada por (a + b).(a – b) . Ou seja, (a + b).(a – b) é a fatoração de a² - b².
- Peça que reparem que em qualquer posição justaposta das figuras, a área não muda. Por isso, podemos escolher uma posição que nos seja melhor para o cálculo da área.
Raio X
Sugira que fatorem a expressão: 4c² - 4 = ?
Convite às famílias
Peça para que seus alunos envolvam seus familiares, próximos neste momento, e acessem o link https://www.youtube.com/watch?v=FLk879D4fos se tiverem dúvidas sobre como dobrar.
Autor: Flávia Aparecida Britto
Mentor: Telma Regina França Rosso
Especialista de área: Sandra Amorim
Habilidade da BNCC
EF09MA09: Compreender os processos de fatoração de expressões algébricas, com base em suas relações com os produtos notáveis, para resolver e elaborar problemas que possam ser representados por equações polinomiais do 2º grau.
Objetivos específicos
Entender que as expressões (x - a).(x+a) e x² + 2ax +a² são equivalentes.
Fatorar expressões do tipo x² -a².
Conceito-chave
Fatoração de expressões algébricas
Recursos necessários
- Projetor para apresentação dos slides da aula;
- Atividades impressas em folhas, coladas no caderno ou não.