Atividade Principal
Plano de Aula
Plano de aula: Ladrilhando com polígonos irregulares
Plano 10 de uma sequência de 10 planos. Veja todos os planos sobre Figuras bidimensionais: elementos e relações
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA.
Autora: Olenêva Sanches Sousa
Mentora: Paula Massi Reis Pires
Revisora Pedagógica: Eliane Zanin
Especialista de área: Pricilla Mendes Cerqueira
Habilidade da BNCC
EF5MA17: Reconhecer, nomear e comparar polígonos, considerando lados, vértices e ângulos, e desenhá-los, utilizando material de desenho ou tecnologias digitais.
Objetivos específicos
- Retomar o conceito de polígonos, na perspectiva de composições de mosaicos irregulares;
- Fazer composições com polígonos não regulares para formar mosaicos irregulares;
- Discutir, coletivamente, sobre polígonos não regulares e suas possibilidades de formação de mosaicos irregulares;
- Pontuar características dos mosaicos irregulares;
- Compor mosaicos irregulares, reconhecendo os polígonos que os compõem.
Conceito-chave
Mosaicos irregulares.
Recursos necessários
Recursos docentes:
- Quadro e pincel;
- Computador;
- Projetor;
- GeoGebra;
- Impressora;
- Internet;
- Atividades impressas da atividade principal;
- Atividade raio x (uma cópia por estudante);
- Apresentação dos 5 slides da Atividade Principal (para ser colocada nos computadores de uso discente e para serem projetadas quando em trabalhos coletivos, como nos momentos 1, especialmente, e 2);
- Cronômetro.
Recursos discentes:
- Lápis;
- Borracha;
- Computador;
- Internet;
- GeoGebra;
- Apresentação em slides da Atividade Principal.
Habilidades BNCC:
Objetivos de aprendizagem
- Retomar o conceito de polígonos, na perspectiva de composições de mosaicos irregulares;
- Fazer composições com polígonos não regulares para formar mosaicos irregulares;
- Discutir, coletivamente, sobre polígonos não regulares e suas possibilidades de formação de mosaicos irregulares;
- Pontuar características dos mosaicos irregulares;
- Compor mosaicos irregulares, reconhecendo os polígonos que os compõem.
Resumo da aula
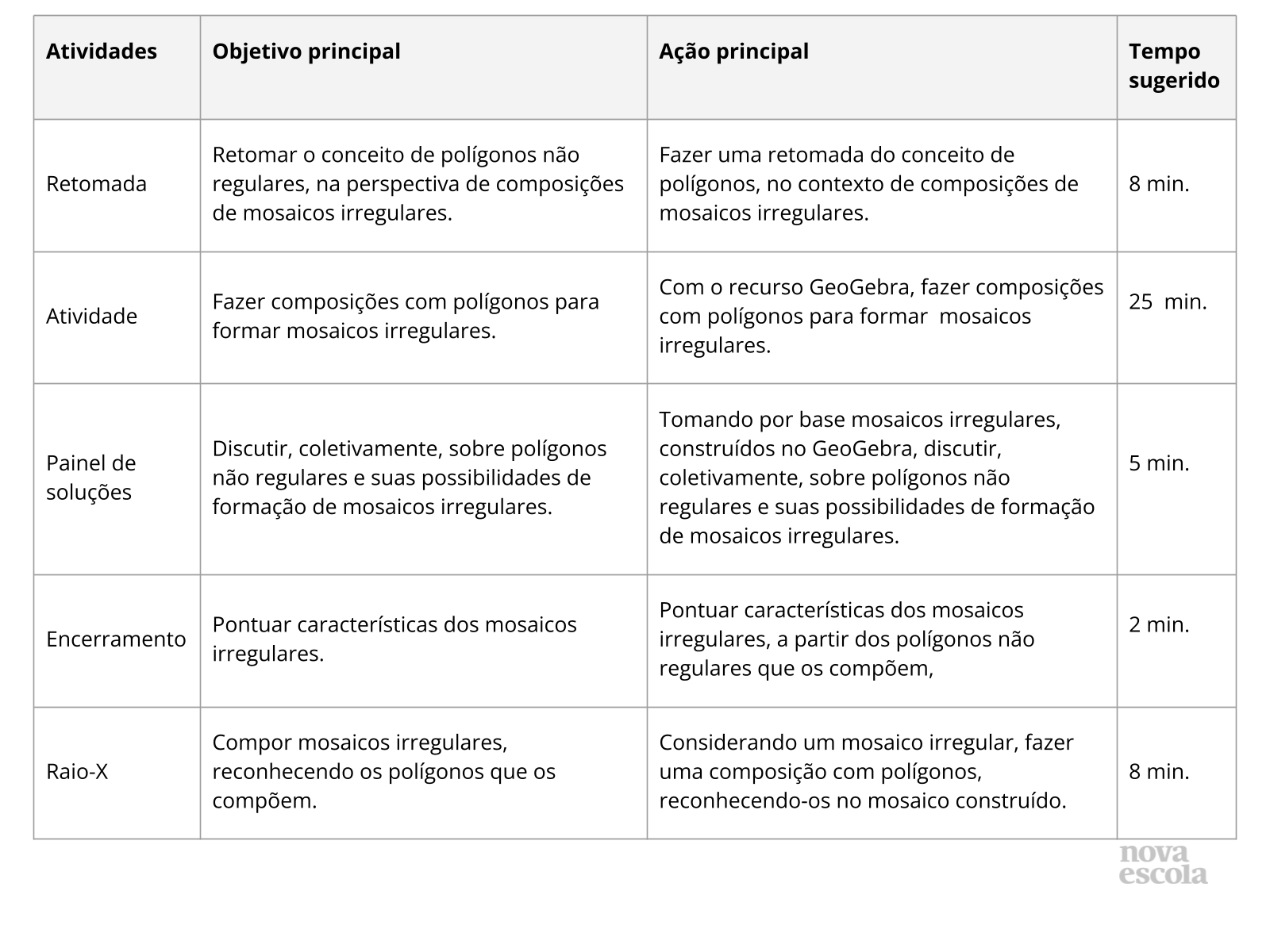
Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
- Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
- Compartilhe o objetivo da aula com os alunos antes de aplicar a proposta.
- Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
- Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.”
Objetivo
Tempo sugerido: 2 minutos
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada
Tempo sugerido: 8 minutos (slides 3, 4 e 5).
Orientação:
- Utilize os slides 3, 4 e 5 como recurso às reflexões acerca das características de um mosaico irregular e dos polígonos não regulares, que os compõem.
- Abaixo, em Discuta com a turma, veja algumas intervenções pertinentes, ponderando a relevância para o seu contexto, no momento.
- Embora esta aula esteja prevista para ser realizada em um laboratório de informática ou com recursos individuais, se necessário, faça complementações no quadro. Em síntese, busque fazer com que todos saibam (ou relembrem) o que é uma composição de polígonos.
- Estando em um laboratório de informática, faça um apresentação dos slides desta aula para que todos possam acompanhar, em seus computadores, nos momentos que envolvem toda a turma e apenas os grupos.
- Apenas como sugestão, questione se os estudantes conhecem letra e música de “Se essa rua fosse minha” e, principalmente, o verbo ladrilhar. Se desejar, fale um pouco sobre essa música popular infantil, de domínio público e sugira que ouçam ou assistam algum vídeo com alguma versão da música. Também como sugestão, existe uma versão rock, com crianças de 5 a 8 anos, que você pode conhecer e, se quiser, indicar para a turma. Para assistir, no YouTube, clique aqui.
Propósito: Retomar o conceito de polígonos irregulares e suas possibilidades de composição em um plano, formando mosaicos.
Discuta com a turma:
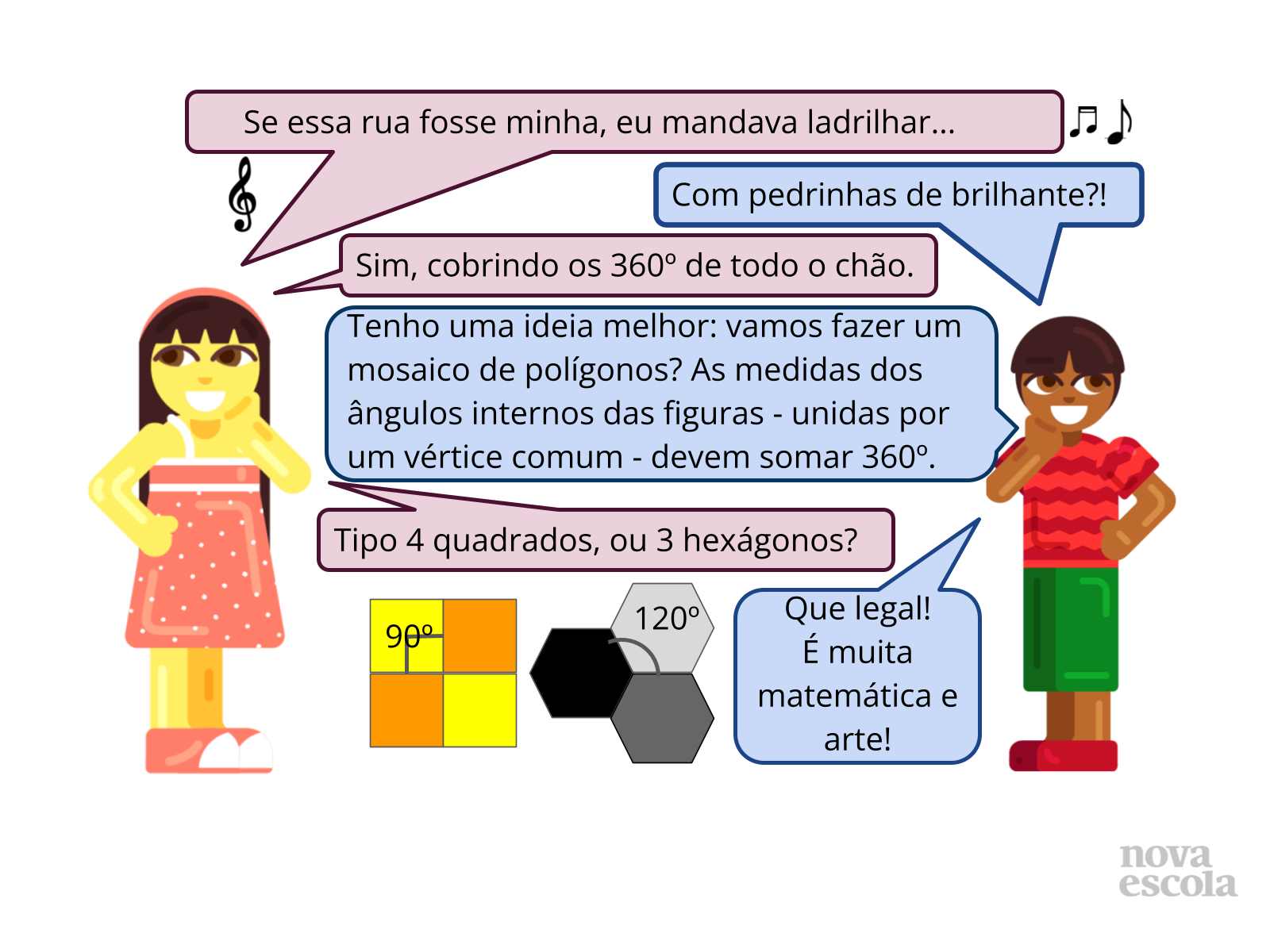
Slide 3 - Foco nos 360º que preenchem um plano: Peça para os estudantes lerem, silenciosamente, o slide. Depois, utilize as “falas” para puxar a discussão:
- Pode me mostrar, com sua mão, o que o garota quis dizer com “cobrir os 360º”?
- Você pode definir, com suas palavras, o que é um mosaico?
- Para você, por que podemos formar mosaicos com polígonos?
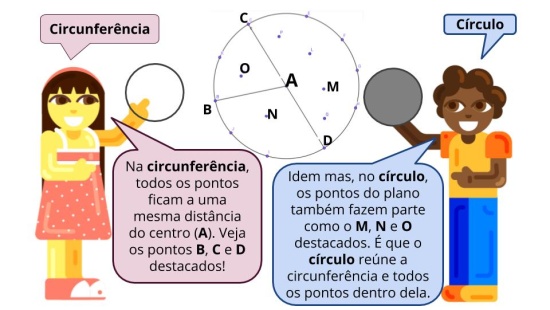
- Poderíamos formar com círculos, por exemplo?
- Na ilustração com o mosaico quadrado, o que representa 90º?
- Quantos 90º tem um quadrado? Por quê?
- Por que, ainda no mosaico quadrado, os 4 quadrados, lado a lado, unidos por um vértice comum, formam um mosaico?
- E no mosaico formado por 3 hexágonos, o que representa 120º?
- Por que precisamos de 4 quadrados no mosaico de quadrados para uni-los lado a lado por um vértice comum?
- Por que precisamos apenas de 3 figuras no mosaico de hexágonos regulares para uni-los lado a lado por um vértice comum?
- O quadrado e o hexágono, utilizados no exemplo deste slide, são polígonos regulares? Por quê?
Retomada
Tempo sugerido: 8 minutos (slides 3, 4 e 5).
Orientação:
- Utilize os slides 3, 4 e 5 como recurso às reflexões acerca das características de um mosaico irregular e dos polígonos não regulares, que os compõem.
- Abaixo, em Discuta com a turma, veja algumas intervenções pertinentes, ponderando a relevância para o seu contexto, no momento.
- Embora esta aula esteja prevista para ser realizada em um laboratório de informática ou com recursos individuais, se necessário, faça complementações no quadro. Em síntese, busque fazer com que todos saibam (ou relembrem) o que é uma composição de polígonos.
- Estando em um laboratório de informática, faça um apresentação dos slides desta aula para que todos possam acompanhar, em seus computadores, nos momentos que envolvem toda a turma e apenas os grupos.
- Apenas como sugestão, questione se os estudantes conhecem letra e música de “Se essa rua fosse minha” e, principalmente, o verbo ladrilhar. Se desejar, fale um pouco sobre essa música popular infantil, de domínio público e sugira que ouçam ou assistam algum vídeo com alguma versão da música. Também como sugestão, existe uma versão rock, com crianças de 5 a 8 anos, que você pode conhecer e, se quiser, indicar para a turma. Para assistir, no YouTube, clique aqui.
Propósito: Retomar o conceito de polígonos irregulares e suas possibilidades de composição em um plano, formando mosaicos.
Discuta com a turma:
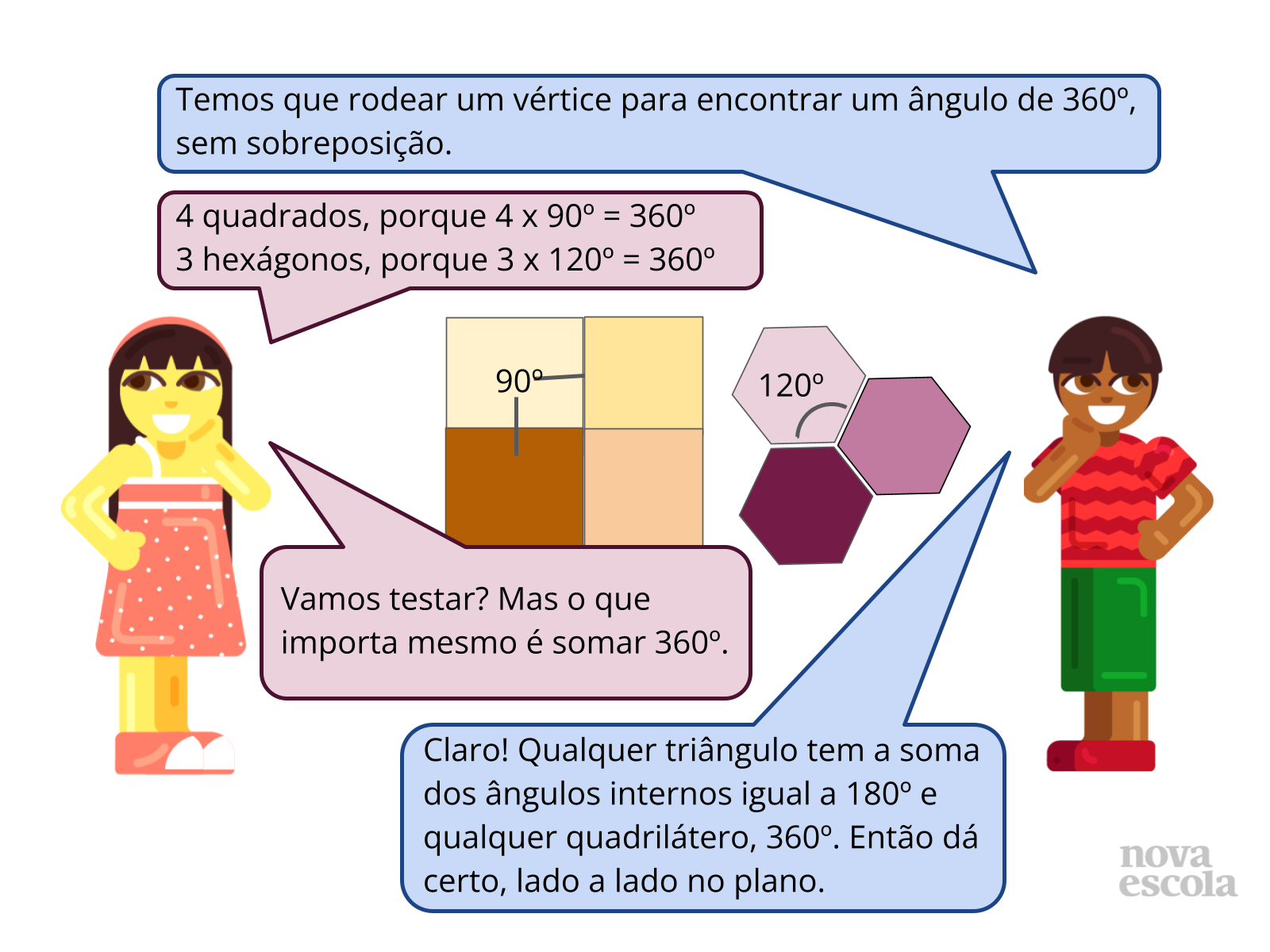
Slide 4 - Foco nos ângulos dos polígonos para formarem mosaicos: Peça para que os estudantes analisem o slide para puxar a discussão:
- Pode me mostrar, nas figuras de mosaicos deste slide, qual a medida do ângulo que rodearia um ponto qualquer? Por que a soma das medidas dos ângulos internos dos polígonos, neste vértice, tem que dar 360º?
- Quem poderia me explicar os cálculos feitos pelo garoto?
- Por que a garota afirma que “precisamos de 6 triângulos de 60º”?
- O que é um quadrilátero?
- Quando a garota afirma que qualquer quadrilátero forma um plano porque tem 360º de ângulo interno, ela está se referindo a polígonos não regulares. Quem pode citar alguns quadriláteros?
- Quando o garoto afirma que “qualquer triângulo tem soma dos ângulos internos 180º, e qualquer quadrilátero, 360º”, podemos afirmar que um quadrilátero pode compor-se de 2 triângulos?
- Quem pode desenhar para testar se essa afirmação é falsa ou verdadeira?
Retomada

Tempo sugerido: 8 minutos (slides 3, 4 e 5).
Orientação:
- Utilize os slides 3, 4 e 5 como recurso às reflexões acerca das características de um mosaico irregular e dos polígonos não regulares, que os compõem.
- Abaixo, em Discuta com a turma, veja algumas intervenções pertinentes, ponderando a relevância para o seu contexto, no momento.
- Embora esta aula esteja prevista para ser realizada em um laboratório de informática ou com recursos individuais, se necessário, faça complementações no quadro. Em síntese, busque fazer com que todos saibam (ou relembrem) o que é uma composição de polígonos.
- Estando em um laboratório de informática, faça um apresentação dos slides desta aula para que todos possam acompanhar, em seus computadores, nos momentos que envolvem toda a turma e apenas os grupos.
- Apenas como sugestão, questione se os estudantes conhecem letra e música de “Se essa rua fosse minha” e, principalmente, o verbo ladrilhar. Se desejar, fale um pouco sobre essa música popular infantil, de domínio público e sugira que ouçam ou assistam algum vídeo com alguma versão da música. Também como sugestão, existe uma versão rock, com crianças de 5 a 8 anos, que você pode conhecer e, se quiser, indicar para a turma. Para assistir, no YouTube, clique aqui.
Propósito: Retomar o conceito de polígonos irregulares e suas possibilidades de composição em um plano, formando mosaicos.
Discuta com a turma:
Slide 5 - Foco nos polígonos não regulares que formam mosaicos irregulares: Peça para os estudantes analisarem o slide e estimule a seguinte discussão:
- Você pode fazer um esboço de um polígono regular qualquer? Quais as características principais desta figura para que ela seja classificada como regular?
- O que faz, então, com que um polígono seja classificado como não regular?
- Segundo o garoto, polígonos não regulares também formam mosaicos. Qual é o critério para que essas figuras sirvam a um mosaico?
- Neste slide, há 2 mosaicos irregulares. Quem pode identificar quais os polígonos que os compõem?
Atividade Principal

Tempo sugerido: 25 minutos (slides 6, 7, 8, 9 e 10).
Orientações:
- Utilize o slide 6 para pontuar, brevemente, os três momentos da atividade, explicando que os dois primeiros serão cumpridos coletivamente, por toda a turma, e o terceiro, em trios, no GeoGebra.
- Esta aula considera que os estudantes já tiveram algum contato anterior com o GeoGebra, mas se não tiveram, sugerimos que oriente os estudantes, em aulas anteriores, para que experimentem o aplicativo em casa. Há 2 opções de uso: online e baixando no computador.
- Preferencialmente, esta aula deve ser desenvolvida em um laboratório de informática que comporte 3 estudantes por computador, e com um projetor; De forma alternativa, podem ser usados recursos tecnológicos individuais, com acesso à internet. O projetor segue recomendado para que sejam realizados os dois primeiros momentos, com todos da turma.
- Em seguida, vá para o slide 7, utilizando-o para apresentar a proposta do primeiro momento da atividade com toda a turma.
- Projete este slide para que todos acompanhem e participem; todos devem estar com o mesmo slide em seus computadores.
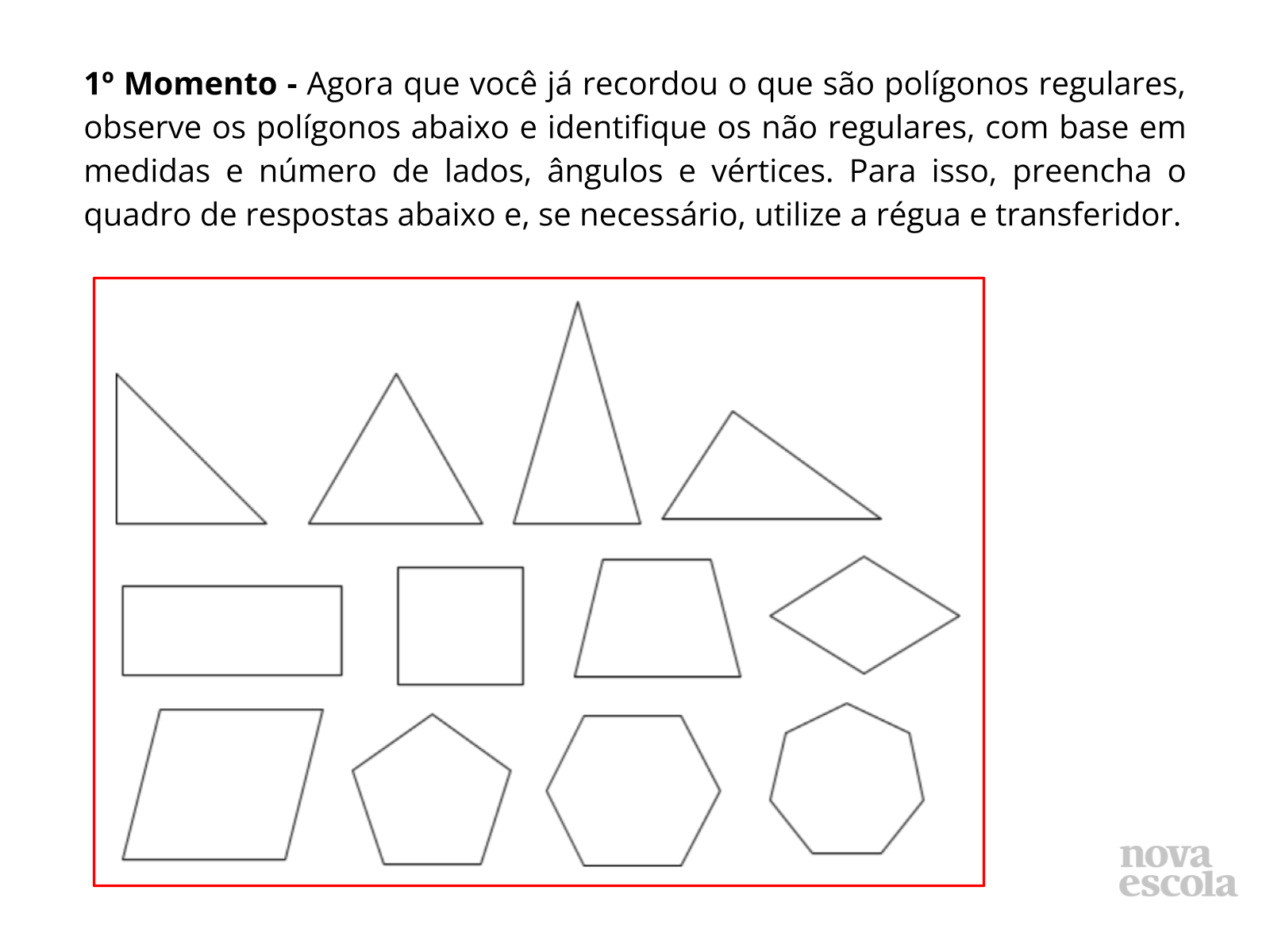
- Faça mediações para toda a turma, iniciando pela numeração dos polígonos.
- Explique que, dentre os polígonos expostos, os alunos deverão reconhecer os polígonos não regulares, com base em medidas e número de lados, ângulos e vértices, preenchendo o quadro de respostas, que será exibido no próximo slide.
- Em seguida, passe para o slide 8. Com o quadro-resposta projetado, vá mediando o seu preenchimento e inserindo os dados solicitados.
- Confira, em Discuta com a Turma, abaixo, algumas questões provocativas para reflexões acerca do conteúdo em pauta, ponderando as relevantes para o seu contexto, no momento.
- Não exceda mais de 5 minutos para esta etapa de análise dos polígonos e preenchimento do quadro-resposta.
- Utilize o slide 9 apenas para dizer que os alunos assistirão a um vídeo sobre as condições para os polígonos regulares formarem mosaico, a fim de ampliar a discussão para as possibilidades de polígonos não regulares formarem mosaicos irregulares.
- Exiba o vídeo, com duração de 2:58 min, para todos e diga que os comentários serão feitos em seguida. Assista ao vídeo aqui.
- Veja, em Discuta com a Turma, questões provocativas sobre o conteúdo do vídeo. Não exceda mais de 3 minutos na discussão.
- Vá para o slide 10 e explique que trabalharão em trio na confecção de mosaicos irregulares.
- Observe se todos estão conectados à internet com o aplicativo GeoGebra.
- Explique que o objetivo da atividade é utilizar o GeoGebra para preencher um determinado plano com polígonos, cobrindo os seus 360º.
- Explique que devem seguir as orientações contidas na própria atividade, mas enfatize que, no GeoGebra, devem usar o ambiente Geometria.
- Observe que, na atividade, é sugerida a exibição de uma malha quadriculada para fazer o desenho, mas que a escolha é opcional.
- Explique também que, a partir do desenho dos polígonos, os trios devem escolher “Polígonos”, no GeoGebra.
- Diga-lhes que estará presente para acompanhar o trabalho dos grupos.
- Explicite que a construção dos mosaicos não deve exceder 15 minutos.
- Imprima previamente a Atividade Principal.
- Considere as seguintes Atividades Complementares para você ver mais possibilidades pedagógicas para o assunto mosaico com polígono:
Atividades Complementares ao Professor:
1ª) Para saber mais sobre ladrilhos, sugerimos a leitura do artigo “Ladrilhamentos”, de Elvia Mureb Sallum, da Matemateca do Instituto de Matemática e Estatística da Universidade de São Paulo (IME-USP). Leia o artigo na íntegra, clicando aqui.
2ª) Para conhecer mais sobre mosaicos, leio o material “Mosaicos” do Laboratório de Ensino de Matemática da Universidade de Brasília (LEMAT-UnB), disponível aqui.
3ª) Material complementar do LEMAT-UnB de Solução das atividades com mosaicos”, disponível aqui.
- Lembre-se de que você dispõe de questões provocadoras, no Guia de Intervenção.
- Confira a Atividade Principal.
Propósito: Fazer composições com polígonos para formar mosaicos irregulares
Atividades complementares:
Atividade Principal
Tempo sugerido: 25 minutos (slides 6, 7, 8, 9 e 10).
Orientações:
- Utilize o slide 6 para pontuar, brevemente, os três momentos da atividade, explicando que os dois primeiros serão cumpridos coletivamente, por toda a turma, e o terceiro, em trios, no GeoGebra.
- Esta aula considera que os estudantes já tiveram algum contato anterior com o GeoGebra, mas se não tiveram, sugerimos que oriente os estudantes, em aulas anteriores, para que experimentem o aplicativo em casa. Há 2 opções de uso: online e baixando no computador.
- Preferencialmente, esta aula deve ser desenvolvida em um laboratório de informática que comporte 3 estudantes por computador, e com um projetor; De forma alternativa, podem ser usados recursos tecnológicos individuais, com acesso à internet. O projetor segue recomendado para que sejam realizados os dois primeiros momentos, com todos da turma.
- Em seguida, vá para o slide 7, utilizando-o para apresentar a proposta do primeiro momento da atividade com toda a turma.
- Projete este slide para que todos acompanhem e participem; todos devem estar com o mesmo slide em seus computadores.
- Faça mediações para toda a turma, iniciando pela numeração dos polígonos.
- Explique que, dentre os polígonos expostos, os alunos deverão reconhecer os polígonos não regulares, com base em medidas e número de lados, ângulos e vértices, preenchendo o quadro de respostas, que será exibido no próximo slide.
- Em seguida, passe para o slide 8. Com o quadro-resposta projetado, vá mediando o seu preenchimento e inserindo os dados solicitados.
- Confira, em Discuta com a Turma, abaixo, algumas questões provocativas para reflexões acerca do conteúdo em pauta, ponderando as relevantes para o seu contexto, no momento.
- Não exceda mais de 5 minutos para esta etapa de análise dos polígonos e preenchimento do quadro-resposta.
- Utilize o slide 9 apenas para dizer que os alunos assistirão a um vídeo sobre as condições para os polígonos regulares formarem mosaico, a fim de ampliar a discussão para as possibilidades de polígonos não regulares formarem mosaicos irregulares.
- Exiba o vídeo, com duração de 2:58 min, para todos e diga que os comentários serão feitos em seguida. Assista ao vídeo aqui.
- Veja, em Discuta com a Turma, questões provocativas sobre o conteúdo do vídeo. Não exceda mais de 3 minutos na discussão.
- Vá para o slide 10 e explique que trabalharão em trio na confecção de mosaicos irregulares.
- Observe se todos estão conectados à internet com o aplicativo GeoGebra.
- Explique que o objetivo da atividade é utilizar o GeoGebra para preencher um determinado plano com polígonos, cobrindo os seus 360º.
- Explique que devem seguir as orientações contidas na própria atividade, mas enfatize que, no GeoGebra, devem usar o ambiente Geometria.
- Observe que, na atividade, é sugerida a exibição de uma malha quadriculada para fazer o desenho, mas que a escolha é opcional.
- Explique também que, a partir do desenho dos polígonos, os trios devem escolher “Polígonos”, no GeoGebra.
- Diga-lhes que estará presente para acompanhar o trabalho dos grupos.
- Explicite que a construção dos mosaicos não deve exceder 15 minutos.
- Imprima previamente a Atividade Principal.
- Considere as seguintes Atividades Complementares para você ver mais possibilidades pedagógicas para o assunto mosaico com polígono:
Atividades Complementares ao Professor:
1ª) Para saber mais sobre ladrilhos, sugerimos a leitura do artigo “Ladrilhamentos”, de Elvia Mureb Sallum, da Matemateca do Instituto de Matemática e Estatística da Universidade de São Paulo (IME-USP). Leia o artigo na íntegra, clicando aqui.
2ª) Para conhecer mais sobre mosaicos, leio o material “Mosaicos” do Laboratório de Ensino de Matemática da Universidade de Brasília (LEMAT-UnB), disponível aqui.
3ª) Material complementar do LEMAT-UnB de Solução das atividades com mosaicos”, disponível aqui.
- Lembre-se de que você dispõe de questões provocadoras, no Guia de Intervenção.
- Confira a Atividade Principal.
Propósito: Fazer composições com polígonos para formar mosaicos irregulares.
Discuta com a turma:
Slide 7:
- Que características deve ter um polígono regular?
- Quais os polígonos regulares apresentados? Por quê?
- Então, quais os que são não regulares?
(São todos os demais, que não possuem igualdade ou regularidade na quantidade e/ou medidas dos seus lados ou ângulos: triângulo retângulo, triângulo isósceles, triângulo escaleno, retângulo, trapézio, losango, paralelogramo).
Atividade Principal
Tempo sugerido: 25 minutos (slides 6, 7, 8, 9 e 10).
Orientações:
- Utilize o slide 6 para pontuar, brevemente, os três momentos da atividade, explicando que os dois primeiros serão cumpridos coletivamente, por toda a turma, e o terceiro, em trios, no GeoGebra.
- Esta aula considera que os estudantes já tiveram algum contato anterior com o GeoGebra, mas se não tiveram, sugerimos que oriente os estudantes, em aulas anteriores, para que experimentem o aplicativo em casa. Há 2 opções de uso: online e baixando no computador.
- Preferencialmente, esta aula deve ser desenvolvida em um laboratório de informática que comporte 3 estudantes por computador, e com um projetor; De forma alternativa, podem ser usados recursos tecnológicos individuais, com acesso à internet. O projetor segue recomendado para que sejam realizados os dois primeiros momentos, com todos da turma.
- Em seguida, vá para o slide 7, utilizando-o para apresentar a proposta do primeiro momento da atividade com toda a turma.
- Projete este slide para que todos acompanhem e participem; todos devem estar com o mesmo slide em seus computadores.
- Faça mediações para toda a turma, iniciando pela numeração dos polígonos.
- Explique que, dentre os polígonos expostos, os alunos deverão reconhecer os polígonos não regulares, com base em medidas e número de lados, ângulos e vértices, preenchendo o quadro de respostas, que será exibido no próximo slide.
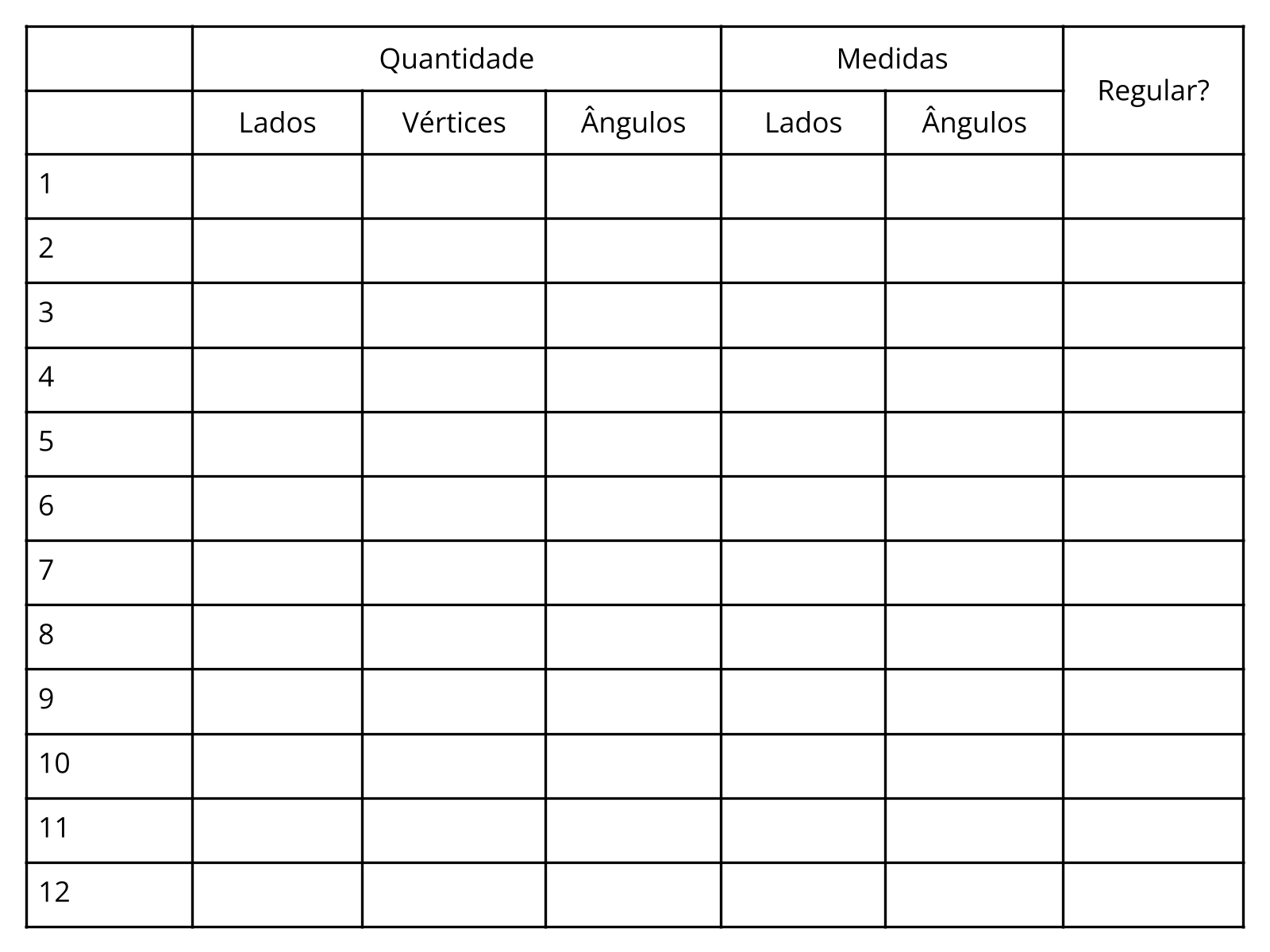
- Em seguida, passe para o slide 8. Com o quadro-resposta projetado, vá mediando o seu preenchimento e inserindo os dados solicitados.
- Confira, em Discuta com a Turma, abaixo, algumas questões provocativas para reflexões acerca do conteúdo em pauta, ponderando as relevantes para o seu contexto, no momento.
- Não exceda mais de 5 minutos para esta etapa de análise dos polígonos e preenchimento do quadro-resposta.
- Utilize o slide 9 apenas para dizer que os alunos assistirão a um vídeo sobre as condições para os polígonos regulares formarem mosaico, a fim de ampliar a discussão para as possibilidades de polígonos não regulares formarem mosaicos irregulares.
- Exiba o vídeo, com duração de 2:58 min, para todos e diga que os comentários serão feitos em seguida. Assista ao vídeo aqui.
- Veja, em Discuta com a Turma, questões provocativas sobre o conteúdo do vídeo. Não exceda mais de 3 minutos na discussão.
- Vá para o slide 10 e explique que trabalharão em trio na confecção de mosaicos irregulares.
- Observe se todos estão conectados à internet com o aplicativo GeoGebra.
- Explique que o objetivo da atividade é utilizar o GeoGebra para preencher um determinado plano com polígonos, cobrindo os seus 360º.
- Explique que devem seguir as orientações contidas na própria atividade, mas enfatize que, no GeoGebra, devem usar o ambiente Geometria.
- Observe que, na atividade, é sugerida a exibição de uma malha quadriculada para fazer o desenho, mas que a escolha é opcional.
- Explique também que, a partir do desenho dos polígonos, os trios devem escolher “Polígonos”, no GeoGebra.
- Diga-lhes que estará presente para acompanhar o trabalho dos grupos.
- Explicite que a construção dos mosaicos não deve exceder 15 minutos.
- Imprima previamente a Atividade Principal.
- Considere as seguintes Atividades Complementares para você ver mais possibilidades pedagógicas para o assunto mosaico com polígono:
Atividades Complementares ao Professor:
1ª) Para saber mais sobre ladrilhos, sugerimos a leitura do artigo “Ladrilhamentos”, de Elvia Mureb Sallum, da Matemateca do Instituto de Matemática e Estatística da Universidade de São Paulo (IME-USP). Leia o artigo na íntegra, clicando aqui.
2ª) Para conhecer mais sobre mosaicos, leio o material “Mosaicos” do Laboratório de Ensino de Matemática da Universidade de Brasília (LEMAT-UnB), disponível aqui.
3ª) Material complementar do LEMAT-UnB de Solução das atividades com mosaicos”, disponível aqui.
- Lembre-se de que você dispõe de questões provocadoras, no Guia de Intervenção.
- Confira a Atividade Principal.
Propósito: Fazer composições com polígonos para formar mosaicos irregulares.
Discuta com a turma:
Slide 8:
- Para o polígono ser considerado irregular, como deve ser o preenchimento do quadro-resposta? (Nem todos os elementos da figura são iguais em quantidade e medida).
- Quais dos polígonos são, portanto, irregulares?
Atividade Principal

Tempo sugerido: 25 minutos (slides 6, 7, 8, 9 e 10).
Orientações:
- Utilize o slide 6 para pontuar, brevemente, os três momentos da atividade, explicando que os dois primeiros serão cumpridos coletivamente, por toda a turma, e o terceiro, em trios, no GeoGebra.
- Esta aula considera que os estudantes já tiveram algum contato anterior com o GeoGebra, mas se não tiveram, sugerimos que oriente os estudantes, em aulas anteriores, para que experimentem o aplicativo em casa. Há 2 opções de uso: online e baixando no computador.
- Preferencialmente, esta aula deve ser desenvolvida em um laboratório de informática que comporte 3 estudantes por computador, e com um projetor; De forma alternativa, podem ser usados recursos tecnológicos individuais, com acesso à internet. O projetor segue recomendado para que sejam realizados os dois primeiros momentos, com todos da turma.
- Em seguida, vá para o slide 7, utilizando-o para apresentar a proposta do primeiro momento da atividade com toda a turma.
- Projete este slide para que todos acompanhem e participem; todos devem estar com o mesmo slide em seus computadores.
- Faça mediações para toda a turma, iniciando pela numeração dos polígonos.
- Explique que, dentre os polígonos expostos, os alunos deverão reconhecer os polígonos não regulares, com base em medidas e número de lados, ângulos e vértices, preenchendo o quadro de respostas, que será exibido no próximo slide.
- Em seguida, passe para o slide 8. Com o quadro-resposta projetado, vá mediando o seu preenchimento e inserindo os dados solicitados.
- Confira, em Discuta com a Turma, abaixo, algumas questões provocativas para reflexões acerca do conteúdo em pauta, ponderando as relevantes para o seu contexto, no momento.
- Não exceda mais de 5 minutos para esta etapa de análise dos polígonos e preenchimento do quadro-resposta.
- Utilize o slide 9 apenas para dizer que os alunos assistirão a um vídeo sobre as condições para os polígonos regulares formarem mosaico, a fim de ampliar a discussão para as possibilidades de polígonos não regulares formarem mosaicos irregulares.
- Exiba o vídeo, com duração de 2:58 min, para todos e diga que os comentários serão feitos em seguida. Assista ao vídeo aqui.
- Veja, em Discuta com a Turma, questões provocativas sobre o conteúdo do vídeo. Não exceda mais de 3 minutos na discussão.
- Vá para o slide 10 e explique que trabalharão em trio na confecção de mosaicos irregulares.
- Observe se todos estão conectados à internet com o aplicativo GeoGebra.
- Explique que o objetivo da atividade é utilizar o GeoGebra para preencher um determinado plano com polígonos, cobrindo os seus 360º.
- Explique que devem seguir as orientações contidas na própria atividade, mas enfatize que, no GeoGebra, devem usar o ambiente Geometria.
- Observe que, na atividade, é sugerida a exibição de uma malha quadriculada para fazer o desenho, mas que a escolha é opcional.
- Explique também que, a partir do desenho dos polígonos, os trios devem escolher “Polígonos”, no GeoGebra.
- Diga-lhes que estará presente para acompanhar o trabalho dos grupos.
- Explicite que a construção dos mosaicos não deve exceder 15 minutos.
- Imprima previamente a Atividade Principal.
- Considere as seguintes Atividades Complementares para você ver mais possibilidades pedagógicas para o assunto mosaico com polígono:
Atividades Complementares ao Professor:
1ª) Para saber mais sobre ladrilhos, sugerimos a leitura do artigo “Ladrilhamentos”, de Elvia Mureb Sallum, da Matemateca do Instituto de Matemática e Estatística da Universidade de São Paulo (IME-USP). Leia o artigo na íntegra, clicando aqui.
2ª) Para conhecer mais sobre mosaicos, leio o material “Mosaicos” do Laboratório de Ensino de Matemática da Universidade de Brasília (LEMAT-UnB), disponível aqui.
3ª) Material complementar do LEMAT-UnB de Solução das atividades com mosaicos”, disponível aqui.
- Lembre-se de que você dispõe de questões provocadoras, no Guia de Intervenção.
- Confira a Atividade Principal.
Propósito: Fazer composições com polígonos para formar mosaicos irregulares.
Discuta com a turma:
Slide 9 (Discussão para construção do mosaico irregular: questões provocadoras - pertinentes à atividade):
- Como cobrir, lado a lado, sem sobrepor?
- Quais características deve ter um polígono para que, unido lado a lado com outros por um mesmo vértice, sirva para cobrir 360º de um tipo qualquer de plano, sem sobreposição?
- Quais polígonos não regulares têm essas características, porque seus ângulos internos somam sempre 360º, e formam um mosaico?
- Por que qualquer tipo de triângulo que não tem a soma de ângulos internos 360º forma um mosaico?
Atividade Principal
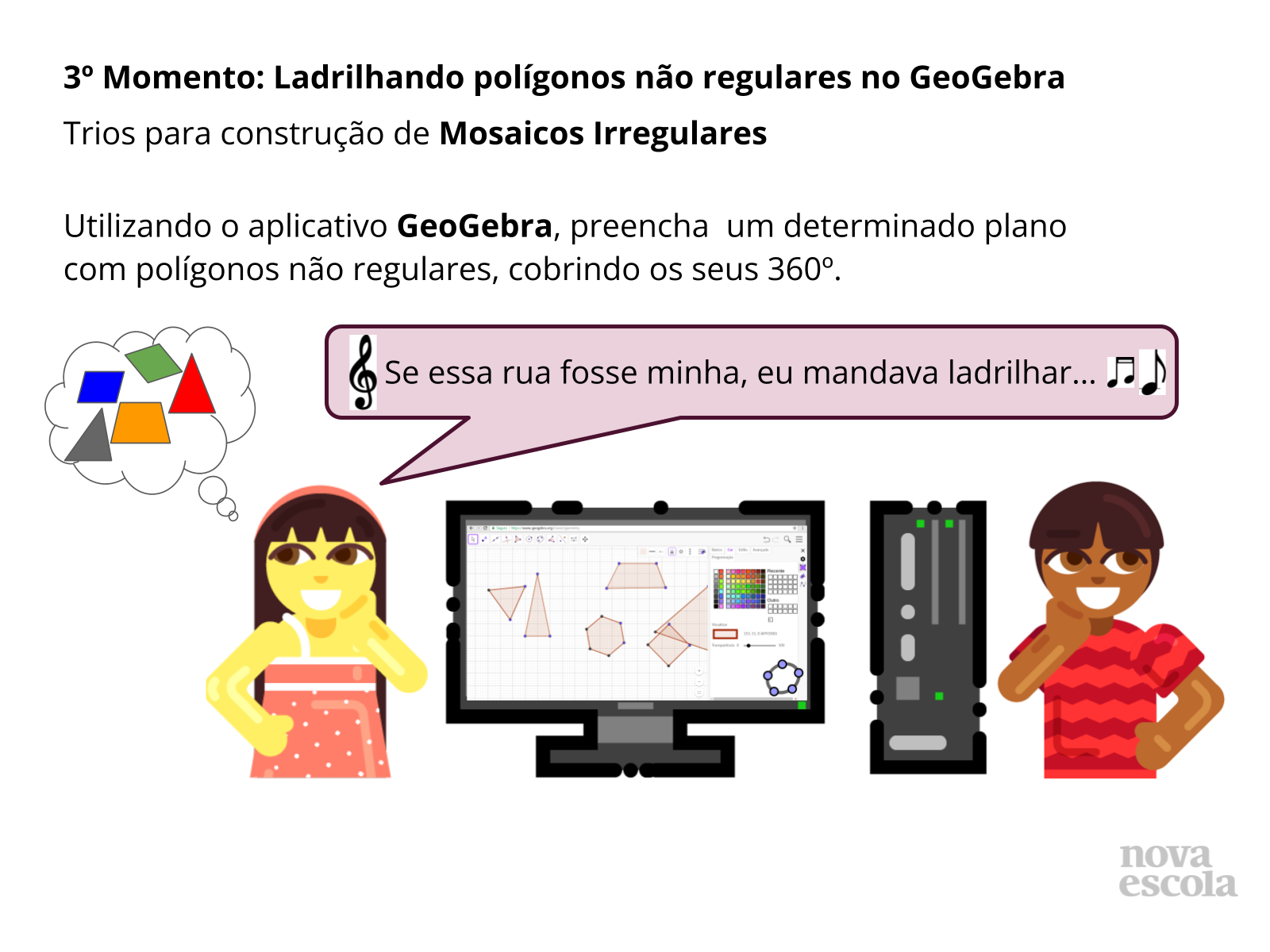
Tempo sugerido: 25 minutos (slides 6, 7, 8, 9 e 10).
Orientações:
- Utilize o slide 6 para pontuar, brevemente, os três momentos da atividade, explicando que os dois primeiros serão cumpridos coletivamente, por toda a turma, e o terceiro, em trios, no GeoGebra.
- Esta aula considera que os estudantes já tiveram algum contato anterior com o GeoGebra, mas se não tiveram, sugerimos que oriente os estudantes, em aulas anteriores, para que experimentem o aplicativo em casa. Há 2 opções de uso: online e baixando no computador.
- Preferencialmente, esta aula deve ser desenvolvida em um laboratório de informática que comporte 3 estudantes por computador, e com um projetor; De forma alternativa, podem ser usados recursos tecnológicos individuais, com acesso à internet. O projetor segue recomendado para que sejam realizados os dois primeiros momentos, com todos da turma.
- Em seguida, vá para o slide 7, utilizando-o para apresentar a proposta do primeiro momento da atividade com toda a turma.
- Projete este slide para que todos acompanhem e participem; todos devem estar com o mesmo slide em seus computadores.
- Faça mediações para toda a turma, iniciando pela numeração dos polígonos.
- Explique que, dentre os polígonos expostos, os alunos deverão reconhecer os polígonos não regulares, com base em medidas e número de lados, ângulos e vértices, preenchendo o quadro de respostas, que será exibido no próximo slide.
- Em seguida, passe para o slide 8. Com o quadro-resposta projetado, vá mediando o seu preenchimento e inserindo os dados solicitados.
- Confira, em Discuta com a Turma, abaixo, algumas questões provocativas para reflexões acerca do conteúdo em pauta, ponderando as relevantes para o seu contexto, no momento.
- Não exceda mais de 5 minutos para esta etapa de análise dos polígonos e preenchimento do quadro-resposta.
- Utilize o slide 9 apenas para dizer que os alunos assistirão a um vídeo sobre as condições para os polígonos regulares formarem mosaico, a fim de ampliar a discussão para as possibilidades de polígonos não regulares formarem mosaicos irregulares.
- Exiba o vídeo, com duração de 2:58 min, para todos e diga que os comentários serão feitos em seguida. Assista ao vídeo aqui.
- Veja, em Discuta com a Turma, questões provocativas sobre o conteúdo do vídeo. Não exceda mais de 3 minutos na discussão.
- Vá para o slide 10 e explique que trabalharão em trio na confecção de mosaicos irregulares.
- Observe se todos estão conectados à internet com o aplicativo GeoGebra.
- Explique que o objetivo da atividade é utilizar o GeoGebra para preencher um determinado plano com polígonos, cobrindo os seus 360º.
- Explique que devem seguir as orientações contidas na própria atividade, mas enfatize que, no GeoGebra, devem usar o ambiente Geometria.
- Observe que, na atividade, é sugerida a exibição de uma malha quadriculada para fazer o desenho, mas que a escolha é opcional.
- Explique também que, a partir do desenho dos polígonos, os trios devem escolher “Polígonos”, no GeoGebra.
- Diga-lhes que estará presente para acompanhar o trabalho dos grupos.
- Explicite que a construção dos mosaicos não deve exceder 15 minutos.
- Imprima previamente a Atividade Principal.
- Considere as seguintes Atividades Complementares para você ver mais possibilidades pedagógicas para o assunto mosaico com polígono:
Atividades Complementares ao Professor:
1ª) Para saber mais sobre ladrilhos, sugerimos a leitura do artigo “Ladrilhamentos”, de Elvia Mureb Sallum, da Matemateca do Instituto de Matemática e Estatística da Universidade de São Paulo (IME-USP). Leia o artigo na íntegra, clicando aqui.
2ª) Para conhecer mais sobre mosaicos, leio o material “Mosaicos” do Laboratório de Ensino de Matemática da Universidade de Brasília (LEMAT-UnB), disponível aqui.
3ª) Material complementar do LEMAT-UnB de Solução das atividades com mosaicos”, disponível aqui.
- Lembre-se de que você dispõe de questões provocadoras, no Guia de Intervenção.
- Confira a Atividade Principal.
Propósito: Fazer composições com polígonos para formar mosaicos irregulares.
Discuta com a turma:
- Slide 10 - utilize este slide apenas para falar que a atividade no GeoGebra irá começar. As provocações já foram colocadas anteriormente.
Discussão das soluções

Tempo sugerido: 5 minutos.
Orientações:
- Como a atividade foi composta de dois momentos de resultados (o 1º e o 3º) e do 2º, de reflexão e discussão sobre a relação entre o conteúdo do momento 1 (polígonos regulares e não regulares) e a construção de mosaicos, no momento 3, já houve discussões durante o percurso e a expectativa é que, durante a 2ª atividade, envolvendo todo o grupo, essa discussão tenha sido calorosa e proveitosa de aprendizagens.
- Peça para que quatro trios (essa quantidade é uma sugestão), espontaneamente, apresentem suas produções, mas compartilhe todos os mosaicos com todos.
- Sugestão: se a escola tiver um site, blogue ou página no Facebook, peça a autorização dos artistas para publicar os mosaicos construídos.
- Durante a exposição dos trios, reforce as questões já mencionadas no Discuta com a Turma dos 4 primeiros slides da Atividade Principal.
- Outras provocações, confira o Guia de Intervenções.
Propósito: Discutir, coletivamente, sobre polígonos não regulares e sobre a formação de mosaicos irregulares.
Discuta com a turma:
- Mostrem-nos por que o seu mosaico é irregular.
- Apresentem-nos as características dos polígonos utilizados que justifiquem a sua classificação como irregular.
Material Complementar:
Encerramento
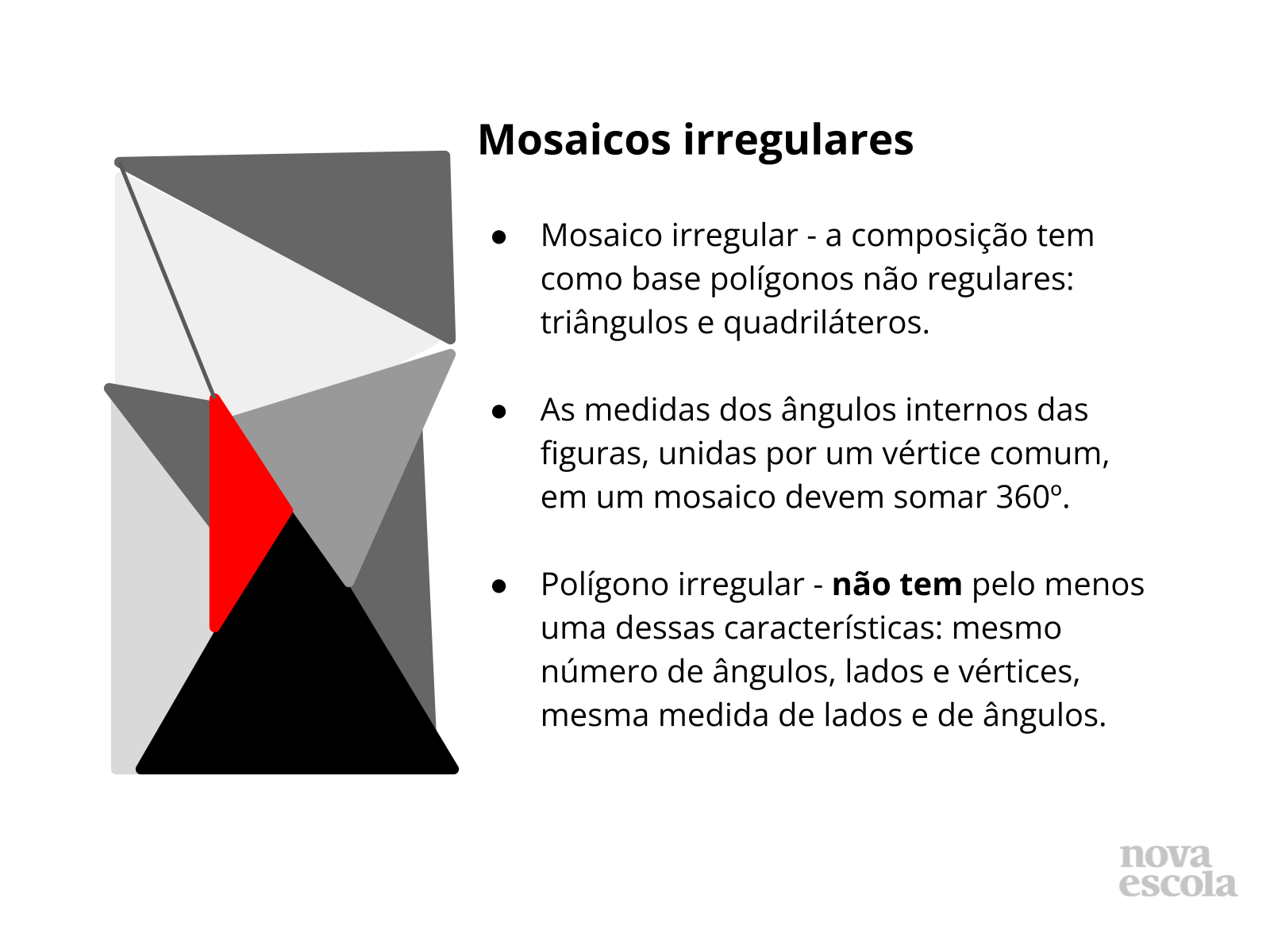
Tempo sugerido: 2 minutos.
Orientações: Este slide pontua o conteúdo trabalhado e sua apresentação deve ser muito breve. Busque enfatizar as características de um mosaico irregular e de sua composição com polígonos não regulares.
Propósito: Sintetizar, de modo ilustrativo, o conteúdo trabalhado.
Raio-X

Tempo sugerido: 8 minutos (slide 13 e 14).
Orientações:
- O slide 13 visa à apresentação breve da avaliação. Utilize-o para explicar a atividade, mas não se estenda por mais de 1 minuto.
- Sem muito rigor na organização da sala, peça aos estudantes para se afastarem ou se arrumarem separadamente para uma atividade que exigirá deles reflexão, atenção e conhecimento sobre polígonos não regulares e sobre sua pertinência em mosaicos irregulares.
- Imprima, previamente, a atividade (slide 14) para que seja realizada individualmente.
Propósito: demonstrar conhecimentos sobre mosaicos irregulares e sobre os polígonos que os compõem.
Discuta com a turma:
- Faça provocações para estimular o estudante a refletir sobre a qualidade da composição de mosaicos irregulares a partir de polígonos não regulares, que os compõem.
- Diversas provocações estão disponíveis no Guia de Intervenção.
Atividades complementares para impressão:
Raio-X
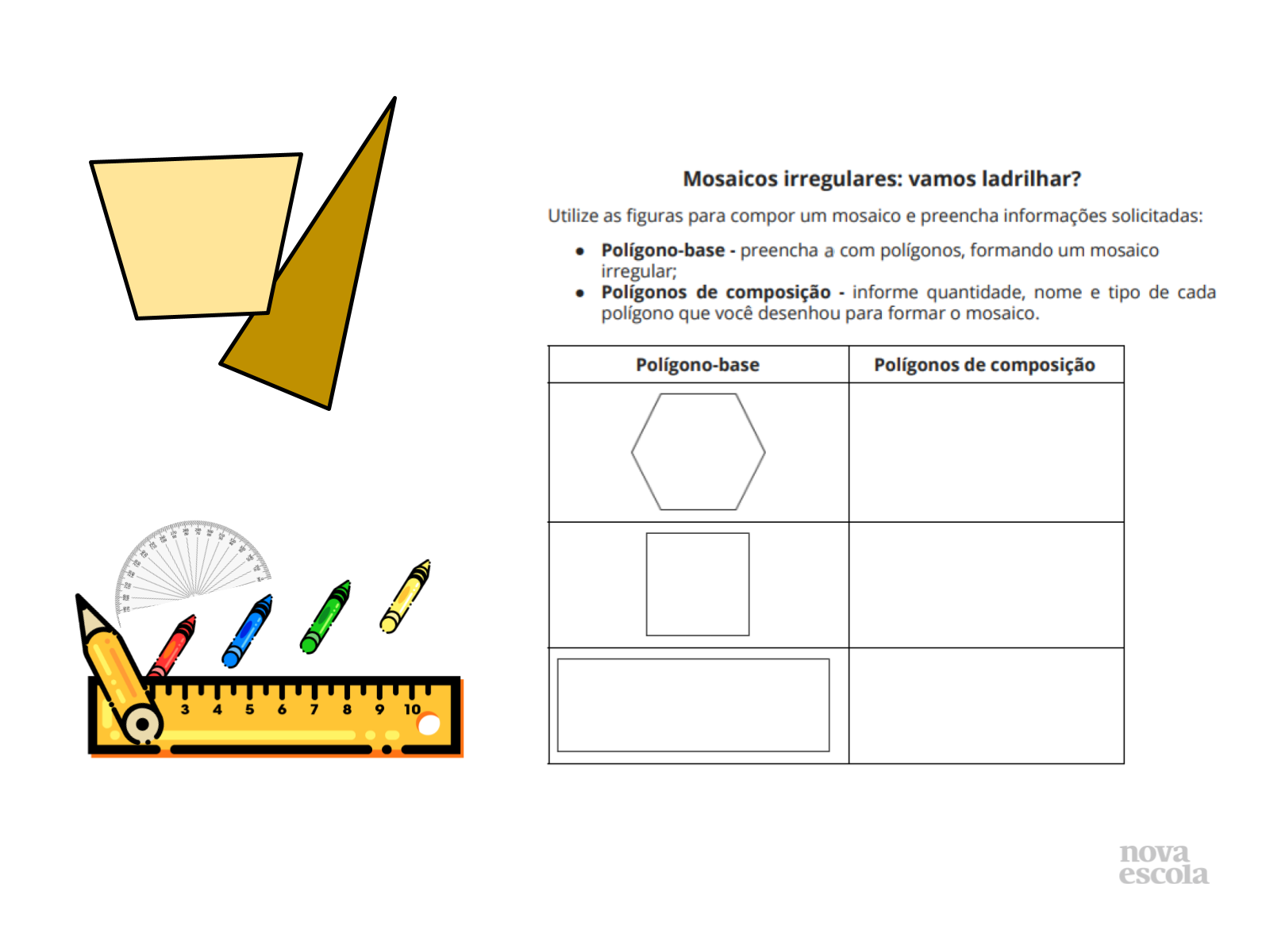
Tempo sugerido: 8 minutos (slide 13 e 14).
Orientações:
- O slide 13 visa à apresentação breve da avaliação. Utilize-o para explicar a atividade, mas não se estenda por mais de 1 minuto.
- Sem muito rigor na organização da sala, peça aos estudantes para se afastarem ou se arrumarem separadamente para uma atividade que exigirá deles reflexão, atenção e conhecimento sobre polígonos não regulares e sobre sua pertinência em mosaicos irregulares.
- Imprima, previamente, a atividade (slide 14) para que seja realizada individualmente.
Propósito: demonstrar conhecimentos sobre mosaicos irregulares e sobre os polígonos que os compõem.
Discuta com a turma:
- Faça provocações para estimular o estudante a refletir sobre a qualidade da composição de mosaicos irregulares a partir de polígonos não regulares, que os compõem.
- Diversas provocações estão disponíveis no Guia de Intervenção.
Atividades complementares para impressão:
Raio-X
Para os Alunos
Para o Professor
Sugestão de adaptação para ensino remoto
Código do plano MAT5_17GEO10
Recursos
- Necessários: -
- Opcionais: GeoGebra
Para este plano, foque na etapa Retomada, Atividade principal e Raio X
Retomada
Professor(a), você pode realizar a Retomada deste plano com seus alunos seja em uma aula síncrona ou assíncrona. Compartilhe com a turma os slides presentes nesta atividade. Compartilhe, em formato de texto, os questionamentos presentes no “Discuta com a turma”. Caso a aula esteja ocorrendo de forma síncrona, permita que os alunos exponham suas reflexões; e, caso esteja ocorrendo de forma assíncrona, os estudantes podem enviar suas reflexões em formato de texto ou áudio.
Atividade principal
Professor(a), mesmo que a atividade proponha que sejam formados grupos, isso não é necessário, todos os alunos podem trabalhar na atividade de forma individual. Compartilhe com a turma as instruções para as etapas de realização da atividade: https://nova-escola-producao.s3.amazonaws.com/3RTd4wMYaTQrpMG746sgjfGS8d55DhHP6MJ9XbNseVQnTSWxtGTBGEkxZGY4/ativprinc-mat5-17geo10.pdf
No 1º momento, oriente que os alunos enumerem os polígonos e os classifiquem. Não é necessário que os alunos reproduzam os desenhos em seus cadernos. Oriente que os alunos reproduzam o quadro em seus cadernos e o complete.
No 3º momento, caso não seja possível a criação no software GeoGebra sugira que os estudantes desenhem em seus cadernos - você pode dar sugestões de imagens buscando a expressão “Mosaico irregular” no Google.
Compartilhe, em formato de texto, os questionamentos presentes no “Discuta com a turma”. Caso a aula esteja ocorrendo de forma síncrona, permita que os alunos exponham suas construções e ideias. Caso a aulas esteja ocorrendo de forma assíncrona, os estudantes podem enviar suas soluções em formato de imagens ou vídeos.
Encerramento
Professor(a), solicite que os alunos registrem em seus cadernos a conclusão que chegaram em relação a criação de mosaicos irregulares. Caso considere viável, compartilhe com os estudantes os slides presentes nesta etapa do plano de aula.
Raio X
O problema proposto no Raio X pode ser enviado aos alunos e solicitado como uma “tarefa” a ser entregue em momento a ser combinado com a turma. Solicite que os alunos reproduzam o quadro em seus cadernos e o complete. Os estudantes podem fotografar suas resoluções e as compartilhar no ambiente que estejam utilizando para interação com a turma.
Obs.: Você pode realizar uma troca caso a aula esteja ocorrendo de forma síncrona. Realize a atividade presente no Raio X e solicite que a atividade presente na Atividade principal seja realizada como tarefa.
Convite às famílias
Professor(a), sugira que os alunos socializem com seus familiares o que aprenderam nesta aula sobre mosaicos irregulares. Uma sugestão de atividade é que os alunos convidem seus familiares a realizarem a atividade proposta na Atividade principal de forma conjunta pensando em diferentes composições de mosaicos.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA.
Autora: Olenêva Sanches Sousa
Mentora: Paula Massi Reis Pires
Revisora Pedagógica: Eliane Zanin
Especialista de área: Pricilla Mendes Cerqueira
Habilidade da BNCC
EF5MA17: Reconhecer, nomear e comparar polígonos, considerando lados, vértices e ângulos, e desenhá-los, utilizando material de desenho ou tecnologias digitais.
Objetivos específicos
- Retomar o conceito de polígonos, na perspectiva de composições de mosaicos irregulares;
- Fazer composições com polígonos não regulares para formar mosaicos irregulares;
- Discutir, coletivamente, sobre polígonos não regulares e suas possibilidades de formação de mosaicos irregulares;
- Pontuar características dos mosaicos irregulares;
- Compor mosaicos irregulares, reconhecendo os polígonos que os compõem.
Conceito-chave
Mosaicos irregulares.
Recursos necessários
Recursos docentes:
- Quadro e pincel;
- Computador;
- Projetor;
- GeoGebra;
- Impressora;
- Internet;
- Atividades impressas da atividade principal;
- Atividade raio x (uma cópia por estudante);
- Apresentação dos 5 slides da Atividade Principal (para ser colocada nos computadores de uso discente e para serem projetadas quando em trabalhos coletivos, como nos momentos 1, especialmente, e 2);
- Cronômetro.
Recursos discentes:
- Lápis;
- Borracha;
- Computador;
- Internet;
- GeoGebra;
- Apresentação em slides da Atividade Principal.