Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.”
Objetivo

Tempo sugerido: 2 min
Orientação: Apresente o objetivo, através da leitura, escrita no quadro ou projeção do mesmo.
Propósito: Apresentar o objetivo de aprendizagem da aula aos alunos.
Deve-se ter como foco a construção do conhecimento de forma que os estudantes concluam, através da atividade principal, generalizações do cálculo da porcentagem.
Também é importante manter o vocabulário matemático, como por exemplo:
- Porcentagem
- Frações centesimais equivalentes
- Quantidade equivalente
Discuta com a turma:
- O que é fração centesimal equivalente?
- O que significa calcular a porcentagem?
Adequações:
- Caso seja possível, pode-se fazer o trabalho com o uso da calculadora para encontrar a equivalência das frações.
- Caso não seja possível a impressão das atividades, pode-se passar no quadro para o estudante copiar.
- Para estudantes com problemas de visão (baixa visão), pode-se solicitar material ampliado, ou desenhar em cartolina, em uma escala grande.
- Para estudantes com outras especificidades, pode-se alterar as variáveis postas nos itens para valores menores, mediando as relações com quantidades menores.
Atividade de aquecimento

Tempo sugerido: 4 min
Orientação: Entregar a atividade para os estudantes, pedir que se reúnam em duplas para a execução da atividade.
Caso não tenha como imprimir, a atividade poderá ser passada no quadro.
Deve-se observar se retomam o conteúdo trabalhado na unidade MAT6_05NUM - Exploração do conceito de fração e operações com frações; análise de equivalência entre frações, comparação; cálculo da fração de um número natural; adição e subtração de frações com denominadores diferente; representações diversas incluindo a reta numerada.
Caso os estudantes não retomam o conteúdo, deve-se trabalhar a unidade sugerida acima, antes de prosseguir.
Materiais complementares para impressão:
Aquecimento
Resolução do Aquecimento
Material complementar:
O link abaixo, é de um vídeo que explica como calcular a porcentagem equivalente de uma quantidade dada em relação ao inteiro, estimulando o uso de planilhas eletrônica.
https://www.youtube.com/watch?v=AHq1NzPIFaw
Propósito: Relembrar como se determina a fração equivalente a uma quantidade dada a partir de um inteiro.
Discuta com a turma:
- Quais as possíveis estratégias?
- Como pode ser determinada essa fração?
Possíveis soluções:
- Divide-se a quantidade dada pelo inteiro apresentado, em seguida simplifica-se a fração.
15/150 = 1/10
10/150 =1/15
Atividade Principal

Tempo sugerido: 15 min
Orientação:
1º momento: peça que, individualmente, leiam e realizem a atividade - 5 minutos
Para esse momento, observe as respostas encontradas individualmente, e, que em seguida, divida as turmas de forma que fiquem juntos os estudantes que obtiveram respostas diferentes.
2º momento: peça que, em duplas, comparem as respostas encontradas e formulem uma resposta da dupla - 5 minutos
Esse é um momento muito importante, pois com a separação planejada das duplas, a discussão deverá ser mediada pelo professor, para que os estudantes troquem e argumentem sobre a sua estratégia de resolução.
3º momento: as duplas deverão compartilhar em um debate coletivo, suas estratégias e respostas - 5 minutos
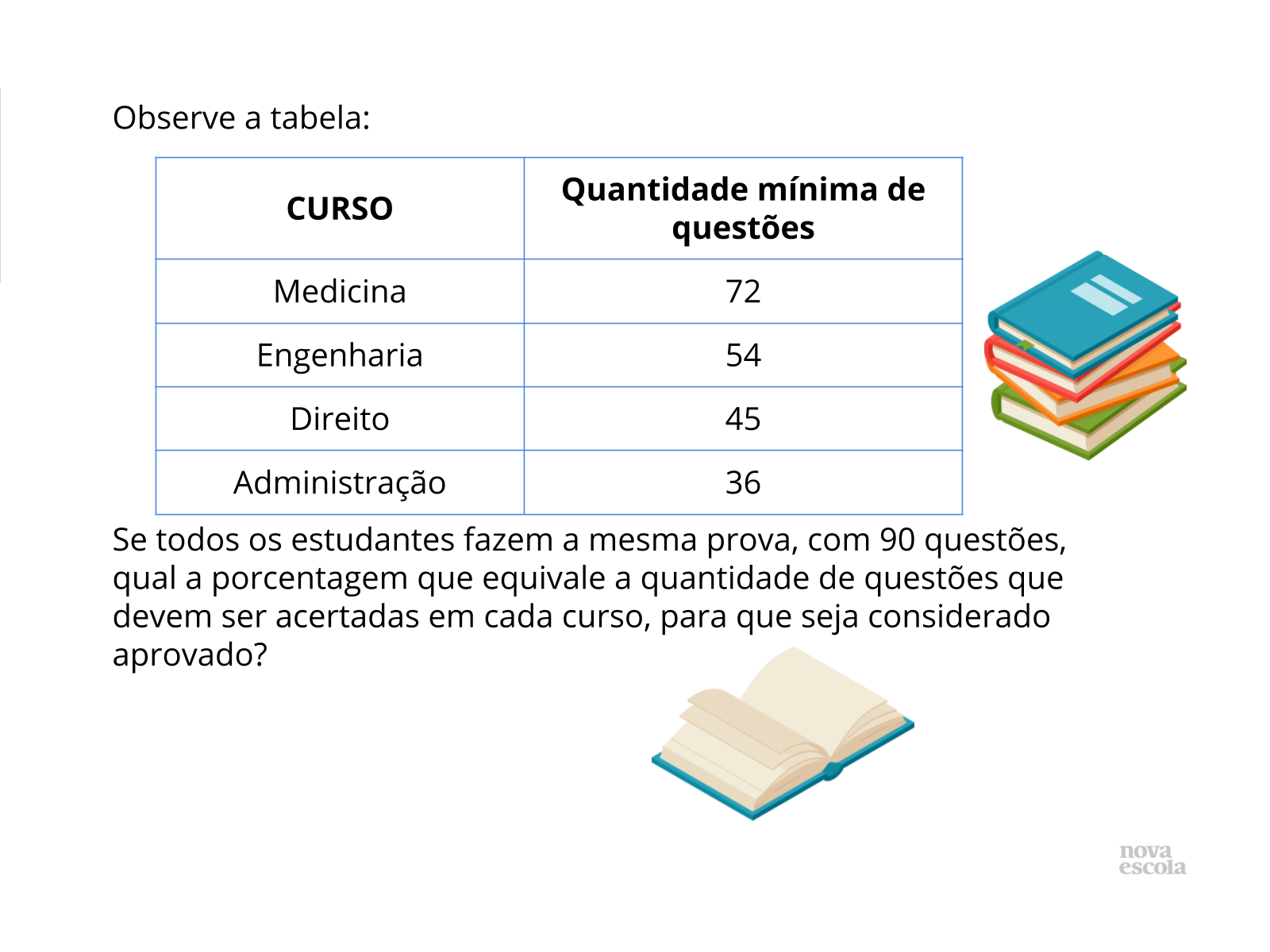
Propósito: Calcular a porcentagem dada a partir do inteiro correspondente.
Discuta com a turma:
- Questione a estratégia usada sempre que perceber que a dupla se distancie do objetivo. Como vocês estão pensando?
- Quais informações importantes podemos retirar do enunciado?
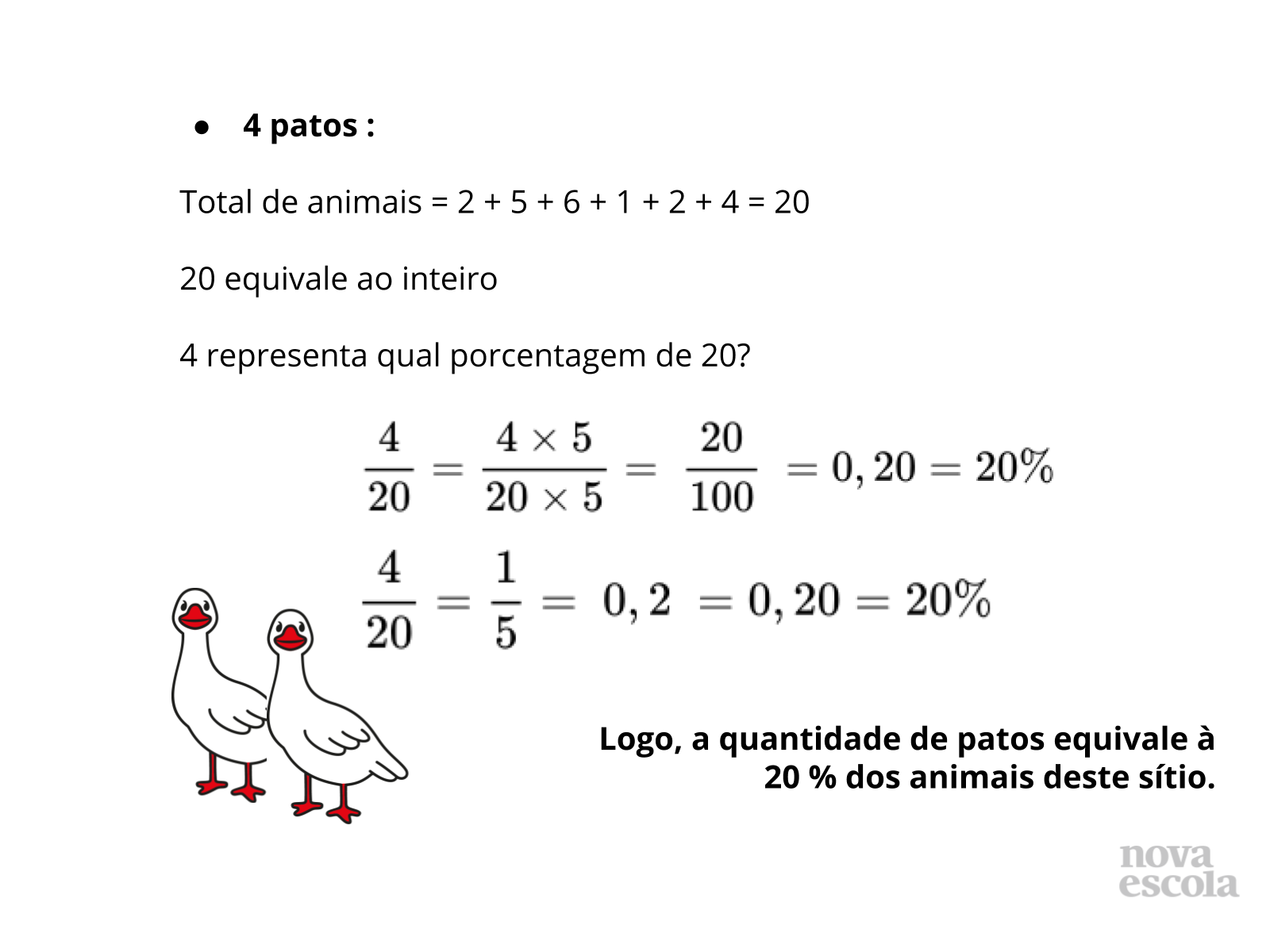
- O que precisamos saber para calcular o que está sendo pedido? (Espera-se que o aluno perceba que ele precisa saber a quantidade total dos animais para saber o percentual que cada um representa no sítio.)
Materiais complementares para impressão:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Painel de Soluções

Tempo sugerido: 15 min (slides 5 a 10)
Orientação:
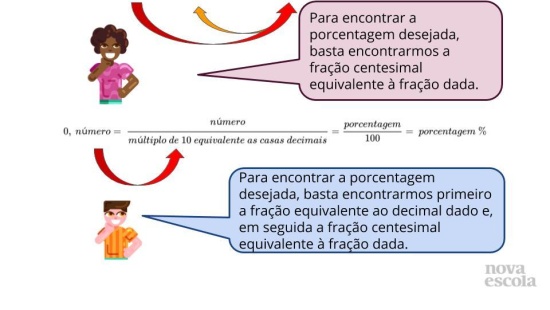
Depois de compartilharem as estratégias apresentadas pelos estudantes, passe essa série de slides. Nela os estudantes verão o passo a passo para o cálculo das porcentagens pedidas na atividade.
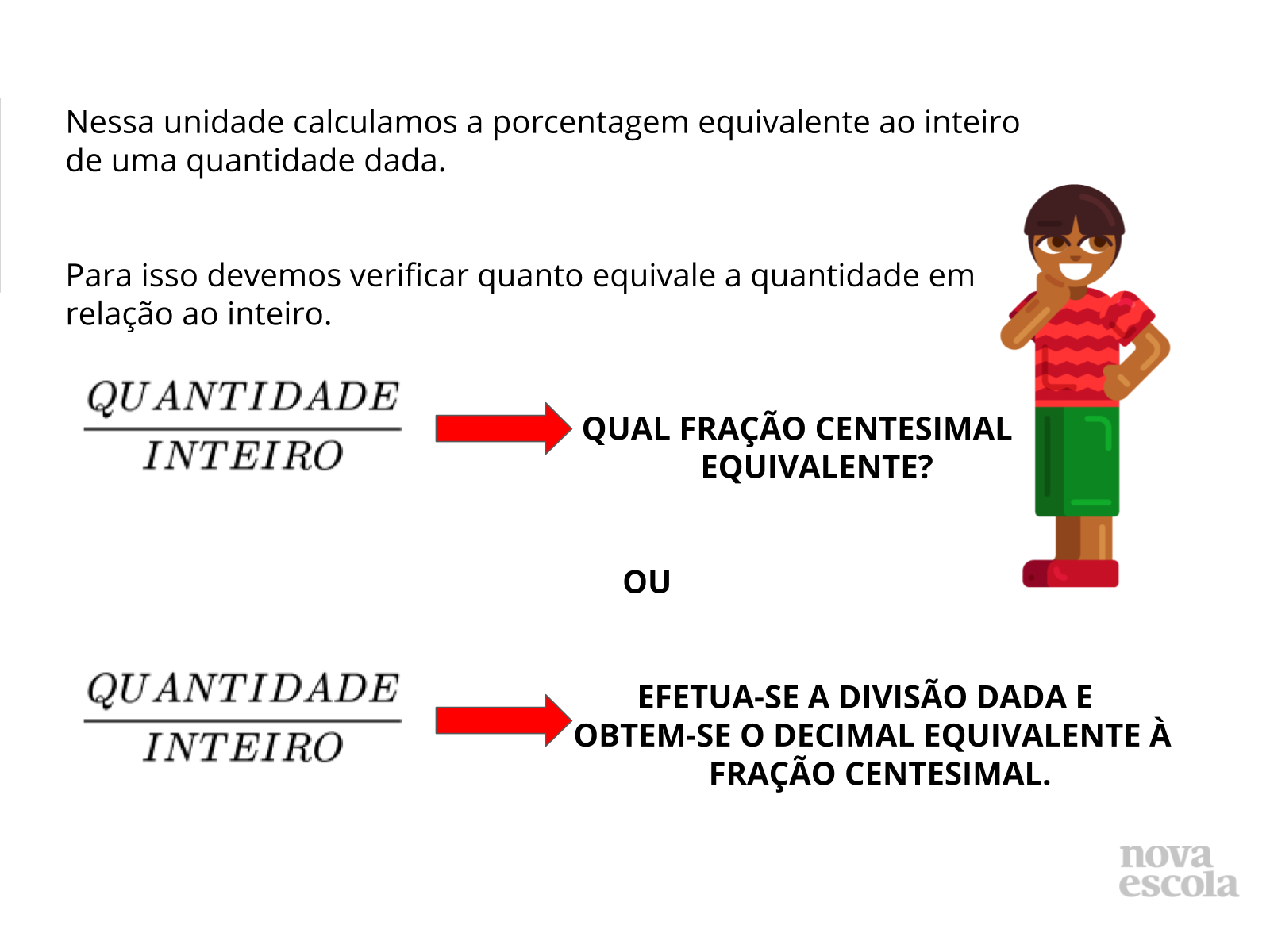
Faça comparações com as estratégias usadas pelos estudantes e elabore coletivamente a generalização de como calcular a porcentagem equivalente à uma quantidade dada.
Propósito: Compartilhar diferentes estratégias de resolução.
Discuta com a turma:
- Como podemos “criar uma regra” para a generalização do cálculo da porcentagem?
- Questione o que significa essa porcentagem em relação ao inteiro?
Painel de Soluções

Tempo sugerido: 15 min (slides 5 a 10)
Orientação:
Depois de compartilharem as estratégias apresentadas pelos estudantes, passe essa série de slides. Nela os estudantes verão o passo a passo para o cálculo das porcentagens pedidas na atividade.
Faça comparações com as estratégias usadas pelos estudantes e elabore coletivamente a generalização de como calcular a porcentagem equivalente à uma quantidade dada.
Propósito: Compartilhar diferentes estratégias de resolução.
Discuta com a turma:
- Como podemos “criar uma regra” para a generalização do cálculo da porcentagem?
- Questione o que significa essa porcentagem em relação ao inteiro?
Painel de Soluções

Tempo sugerido: 15 min (slides 5 a 10)
Orientação:
Depois de compartilharem as estratégias apresentadas pelos estudantes, passe essa série de slides. Nela os estudantes verão o passo a passo para o cálculo das porcentagens pedidas na atividade.
Faça comparações com as estratégias usadas pelos estudantes e elabore coletivamente a generalização de como calcular a porcentagem equivalente à uma quantidade dada.
Propósito: Compartilhar diferentes estratégias de resolução.
Discuta com a turma:
- Como podemos “criar uma regra” para a generalização do cálculo da porcentagem?
- Questione o que significa essa porcentagem em relação ao inteiro?
Painel de Soluções

Tempo sugerido: 15 min (slides 5 a 10)
Orientação:
Depois de compartilharem as estratégias apresentadas pelos estudantes, passe essa série de slides. Nela os estudantes verão o passo a passo para o cálculo das porcentagens pedidas na atividade.
Faça comparações com as estratégias usadas pelos estudantes e elabore coletivamente a generalização de como calcular a porcentagem equivalente à uma quantidade dada.
Propósito: Compartilhar diferentes estratégias de resolução.
Discuta com a turma:
- Como podemos “criar uma regra” para a generalização do cálculo da porcentagem?
- Questione o que significa essa porcentagem em relação ao inteiro?
Painel de Soluções

Tempo sugerido: 15 min (slides 5 a 10)
Orientação:
Depois de compartilharem as estratégias apresentadas pelos estudantes, passe essa série de slides. Nela os estudantes verão o passo a passo para o cálculo das porcentagens pedidas na atividade.
Faça comparações com as estratégias usadas pelos estudantes e elabore coletivamente a generalização de como calcular a porcentagem equivalente à uma quantidade dada.
Propósito: Compartilhar diferentes estratégias de resolução.
Discuta com a turma:
- Como podemos “criar uma regra” para a generalização do cálculo da porcentagem?
- Questione o que significa essa porcentagem em relação ao inteiro?
Painel de Soluções
Tempo sugerido: 15 min (slides 5 a 10)
Orientação:
Depois de compartilharem as estratégias apresentadas pelos estudantes, passe essa série de slides. Nela os estudantes verão o passo a passo para o cálculo das porcentagens pedidas na atividade.
Faça comparações com as estratégias usadas pelos estudantes e elabore coletivamente a generalização de como calcular a porcentagem equivalente à uma quantidade dada.
Propósito: Compartilhar diferentes estratégias de resolução.
Discuta com a turma:
- Como podemos “criar uma regra” para a generalização do cálculo da porcentagem?
- Questione o que significa essa porcentagem em relação ao inteiro?
Encerramento
Tempo sugerido: 6 minutos
Orientação: Encerre com os estudantes fazendo um resumo da aula e retomando o cálculo da porcentagem de uma quantidade dada em relação ao inteiro.
Propósito: retomar o conceito apresentado na unidade.
Discuta com a turma:
- Existe alguma outra estratégia?