Atividade principal
Plano de Aula
Plano de aula: Adição e subtração de Decimais
Plano 2 de uma sequência de 10 planos. Veja todos os planos sobre Descobrindo e ampliando as operações com racionais.
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Kurth Correa Waldhelm
Mentora: Débora Vieira de Moraes
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF06MA10 - Resolver e elaborar problemas com números racionais positivos na representação decimal, envolvendo as quatro operações fundamentais e potenciação, por meio de estratégias diversas, utilizando estimativas e arredondamentos para verificar a razoabilidade de respostas, com e sem o uso de calculadora.
Objetivos específicos
Conceituar, resolver e elaborar estratégias de cálculo para adição e subtração de números positivos na forma decimal.
Conceito-chave
Adição e subtração de decimais.
Recursos necessários
- Folha de papel A4 branca;
- Atividades impressas em folhas, coladas no caderno ou não;
- Calculadora ou celular (se possível).
Habilidades BNCC:
Objetivos de aprendizagem
Conceituar, resolver e elaborar estratégias de cálculo para adição e subtração de números positivos na forma decimal.
Resumo da aula
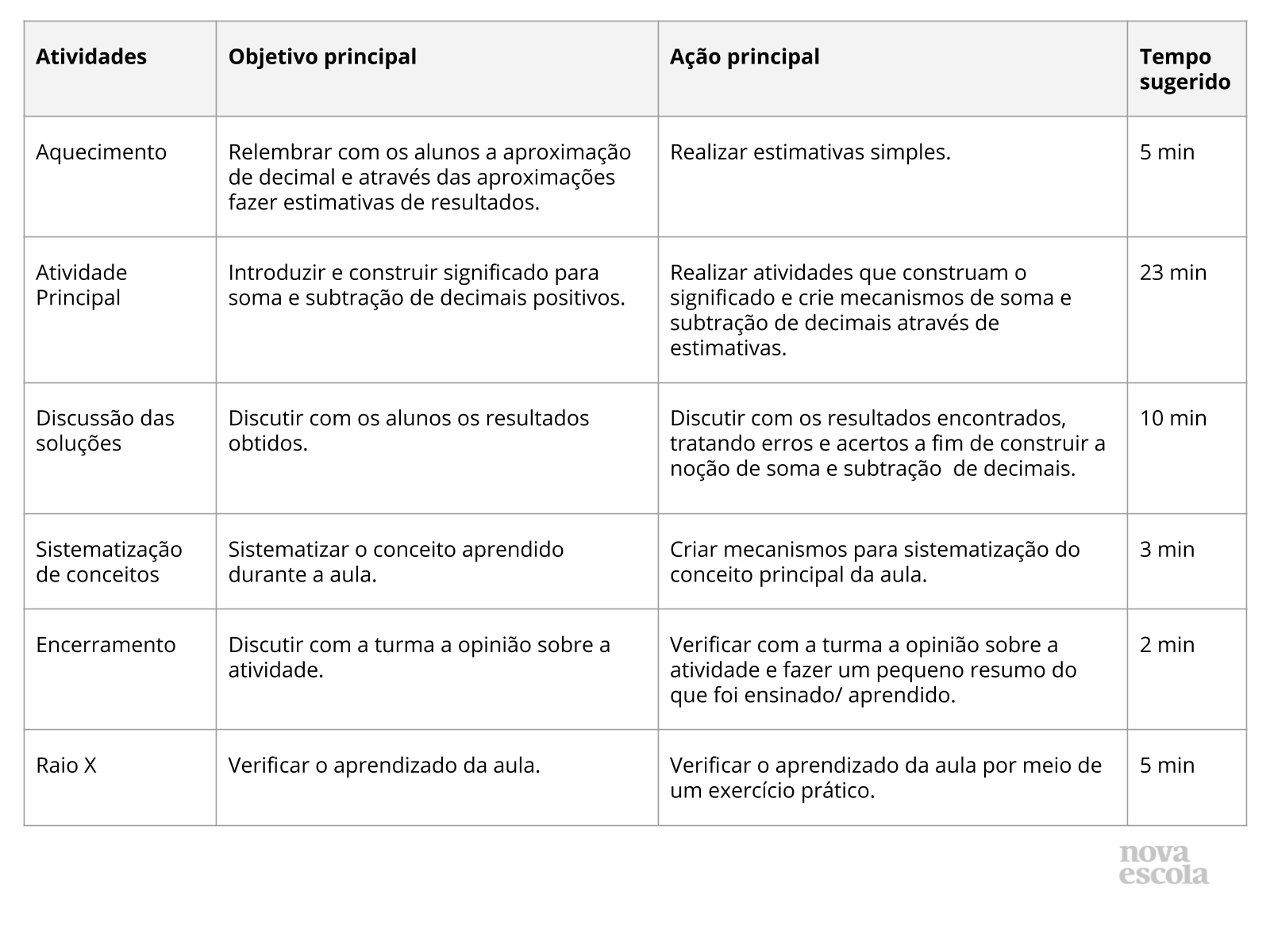
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Descreva para turma o objetivo da aula que é conceituar e construir significado para a soma e subtração de decimais através da resolução de situações problemas, é importante ressaltar que o esforço produtivo dos alunos devem ser incentivado a fim de que os mesmos sejam capazes de criar estratégias para somar e subtrair decimais.
Propósito: Relembrar conceitos já estudados utilizando-os para a construção do significado e entendimento de soma e subtração de decimais. Na presente aula os alunos terão acesso a atividades que propiciam a construção deste aprendizado.
Aquecimento

Tempo sugerido: 5 minutos.
Orientação: Se possível use o projetor ou faça um esboço deste slide.
Discuta com a turma: a aproximação de decimais para inteiros, a fim de as utilizar futuramente para fazer estimativas, ajudando assim a construir um significado para soma e subtração de decimais. Se necessário relembre com os alunos as regras de aproximação.
Propósito: Ambientar a turma para as atividades que virão a seguir.
Discuta com a Turma: Discuta nesta etapa a importância dos números decimais no nosso dia a dia, pedindo para eles citarem exemplos de onde encontramos números decimais em nosso cotidiano. Além disso discuta a razoabilidade de se trabalhar com aproximações para emitir respostas significativas.
Assim usa-se como regra:
Quando o número que sucede o dígito o qual se quer aproximar é menor 5, mantém-se o número. Quando o número que o sucede é maior ou igual 5, soma-se ao dígito de aproximação uma (1) unidade.
Ex: 40,67 aproximando para casas dos décimos obtemos 40,7, aproximando para as unidade 41.
20, 13 aproximando-se para as casas dos décimos obtemos 20,1. Aproximando-se para as casas da unidades obtem-se 20.
20,05 ao se aproximar para casa dos décimos obtemos 20,1, porém ao se aproximar para casa das unidades obtemos 20.
Vale ressaltar que tratamos aqui de convenções matemáticas utilizadas para tratar de aproximações, existem outras possibilidades.
Discuta ainda neste momento o uso dos numero decimais no nosso dia a dia e sua importância, bem como suas representações com inúmeras casas decimais, como por exemplo o número 1 que pode ser escrito como 1,0 ou 1,00 etc.
Respostas:
1) Possibilidades de respostas são: dinheiro, distancia, temperatura, peso, comprimento.
2) Escrevas os números a seguir com quatro casas decimais:
a) 21 = 21,0000
b) 21,1 = 21,1000
c) 21,01= 21,0100
d) 21,001= 21,0010
e) Qual é o maior? 21,1
2) Faça a aproximação adequada para a casa sublinhada:
a) 13,05 = 13,1
b) 101,593 = 101,59
c) 29,00001 = 29,0
d)987,809= 988
Atividade Principal

Tempo sugerido: 23 minutos (slides 4 a 7).
Orientação: Imprima a atividade para os alunos e se possível projete a mesma, para que todos possam acompanhar. Divida a classe em grupos e deixem que eles façam as atividades. Caminhe pela sala, faça perguntas e caso precise recorra ao guia de intervenção em anexo.
Propósito: O Objetivo da atividade é fazer com que o aluno realize a soma e subtração de decimais, construir o significado para essa operação se utilizando de aproximações e estimativas, porém é possível também que o alunos se utilize das operações na forma de fração para tal, e ao final crie um método para realizar essa operação.
Discuta com a turma: A importância da estimativa para resolução de problemas significativos, que em muitos casos, uma boa aproximação resolve ou ajuda a ter uma ideia da resolução do problema. O cálculo exato é muito importante, porém com o advento da tecnologia dificilmente faremos contas de 3, 4 ou mais casas decimais sem o auxílio de alguma ferramenta.
Materiais complementares para impressão:
Atividade Principal
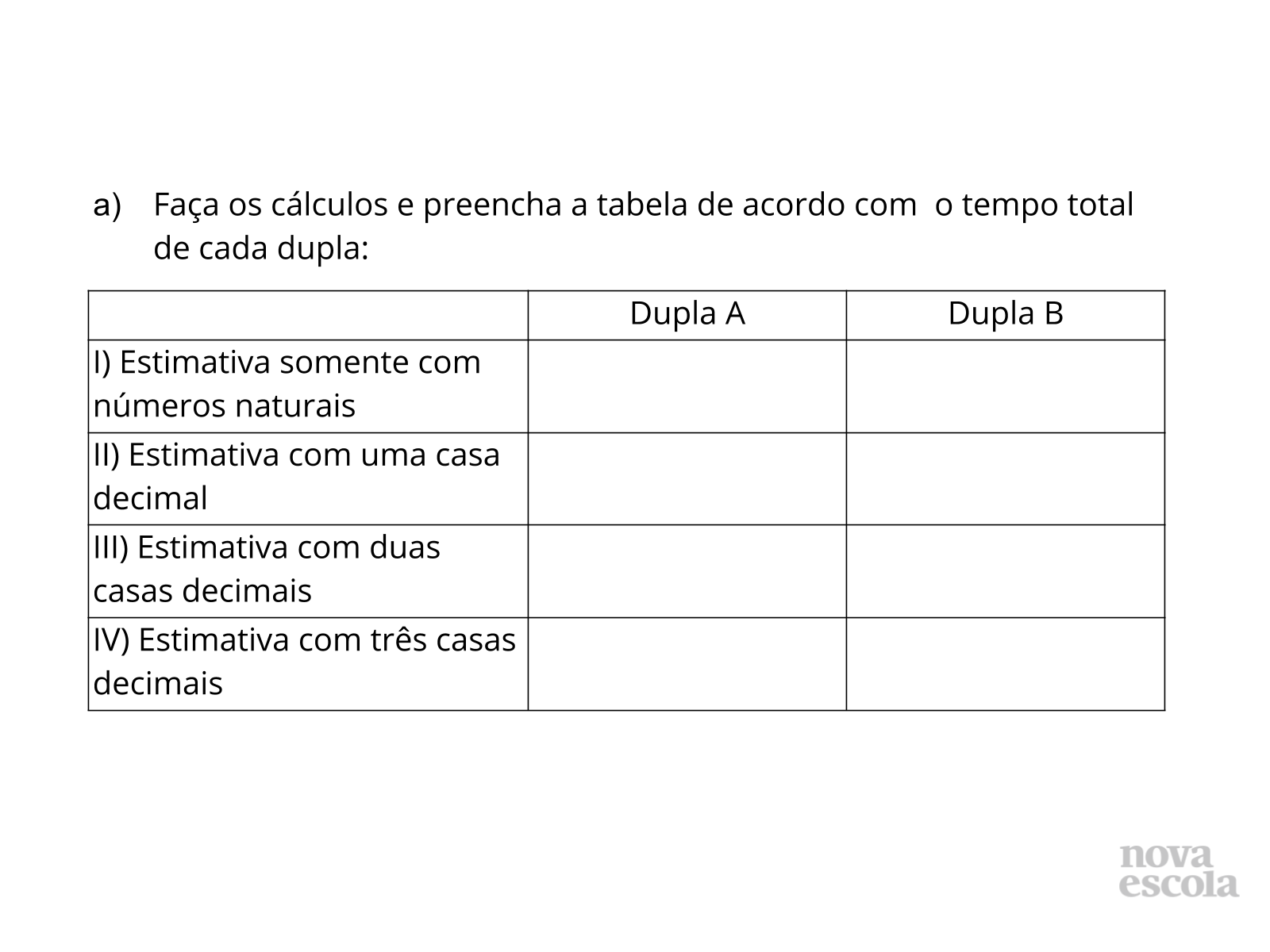
Tempo sugerido: 23 minutos (slides 4 a 7).
Orientação: Imprima a atividade para os alunos e se possível projete a mesma, para que todos possam acompanhar. Divida a classe em grupos e deixem que eles façam as atividades. Caminhe pela sala, faça perguntas e caso precise recorra ao guia de intervenção em anexo.
Propósito: O Objetivo da atividade é fazer com que o aluno realize a soma e subtração de decimais, construir o significado para essa operação se utilizando de aproximações e estimativas, porém é possível também que o alunos se utilize das operações na forma de fração para tal, e ao final crie um método para realizar essa operação.
Discuta com a turma: A importância da estimativa para resolução de problemas significativos, que em muitos casos, uma boa aproximação resolve ou ajuda a ter uma ideia da resolução do problema. O cálculo exato é muito importante, porém com o advento da tecnologia dificilmente faremos contas de 3, 4 ou mais casas decimais sem o auxílio de alguma ferramenta.
Atividade Principal

Tempo sugerido: 23 minutos (slides 4 a 7).
Orientação: Imprima a atividade para os alunos e se possível projete a mesma, para que todos possam acompanhar. Divida a classe em grupos e deixem que eles façam as atividades. Caminhe pela sala, faça perguntas e caso precise recorra ao guia de intervenção em anexo.
Propósito: O Objetivo da atividade é fazer com que o aluno realize a soma e subtração de decimais, construir o significado para essa operação se utilizando de aproximações e estimativas, porém é possível também que o alunos se utilize das operações na forma de fração para tal, e ao final crie um método para realizar essa operação.
Discuta com a turma: A importância da estimativa para resolução de problemas significativos, que em muitos casos, uma boa aproximação resolve ou ajuda a ter uma ideia da resolução do problema. O cálculo exato é muito importante, porém com o advento da tecnologia dificilmente faremos contas de 3, 4 ou mais casas decimais sem o auxílio de alguma ferramenta.
Atividade Principal

Tempo sugerido: 23 minutos (slides 4 a 7).
Orientação: Imprima a atividade para os alunos e se possível projete a mesma, para que todos possam acompanhar. Divida a classe em grupos e deixem que eles façam as atividades. Caminhe pela sala, faça perguntas e caso precise recorra ao guia de intervenção em anexo.
Propósito: O Objetivo da atividade é fazer com que o aluno realize a soma e subtração de decimais, construir o significado para essa operação se utilizando de aproximações e estimativas, porém é possível também que o alunos se utilize das operações na forma de fração para tal, e ao final crie um método para realizar essa operação.
Discuta com a turma: A importância da estimativa para resolução de problemas significativos, que em muitos casos, uma boa aproximação resolve ou ajuda a ter uma ideia da resolução do problema. O cálculo exato é muito importante, porém com o advento da tecnologia dificilmente faremos contas de 3, 4 ou mais casas decimais sem o auxílio de alguma ferramenta.
Discussão das Soluções

Tempo sugerido: 5 minutos.
Orientação: Discuta com os alunos os caminhos feitos e as respostas, se possível utilize o quadro e liste as diferentes formas de raciocínio. Dê ênfase aos erros e como eles podem construir caminhos para acertos.
Propósito: Comparar e discutir as soluções encontradas.
Discuta com a turma: Pergunte aos alunos, quais caminhos eles tomaram para chegar às respostas, se possível anote-os para discussão. É importante também fazer um levantamento dos erros cometidos, a fim de fazer uma reflexão do porque eles ocorreram e como eles podem propiciar o caminho para acertos.
Se possível utilize com os alunos uma calculadora para conferir os resultados obtidos.
Discussão de Soluções

Tempo sugerido: 5 minutos.
Orientação: Discuta com os alunos os caminhos feitos e as respostas, se possível utilize o quadro e liste as diferentes formas de raciocínio. Dê ênfase aos erros e como eles podem construir caminhos para acertos.
Propósito: Comparar e discutir as soluções encontradas.
Discuta com a turma: Pergunte aos alunos, quais caminhos eles tomaram para chegar às respostas, se possível anote-os para discussão. É importante também fazer um levantamento dos erros cometidos, a fim de fazer uma reflexão do porque eles ocorreram e como eles podem propiciar o caminho para acertos.
Se possível utilize com os alunos uma calculadora pra conferir os resultados obtidos.
Discussão de Soluções

Tempo sugerido: 5 minutos.
Orientação: Discuta com os alunos os caminhos feitos e as respostas, se possível utilize o quadro e liste as diferentes formas de raciocínio. Dê ênfase aos erros e como eles podem construir caminhos para acertos.
Propósito: Comparar e discutir as soluções encontradas.
Discuta com a turma: Pergunte aos alunos, quais caminhos eles tomaram para chegar às respostas, se possível anote-os para discussão. É importante também fazer um levantamento dos erros cometidos, a fim de fazer uma reflexão do porque eles ocorreram e como eles podem propiciar o caminho para acertos.
Se possível utilize com os alunos uma calculadora pra conferir os resultados obtidos.
Discussão de Soluções

Tempo sugerido: 5 minutos.
Orientação: Discuta com os alunos os caminhos feitos e as respostas, se possível utilize o quadro e liste as diferentes formas de raciocínio. Dê ênfase aos erros e como eles podem construir caminhos para acertos.
Propósito: Comparar e discutir as soluções encontradas.
Discuta com a turma: Pergunte aos alunos, quais caminhos eles tomaram para chegar às respostas, se possível anote-os para discussão. É importante também fazer um levantamento dos erros cometidos, a fim de fazer uma reflexão do porque eles ocorreram e como eles podem propiciar o caminho para acertos.
Se possível utilize com os alunos uma calculadora pra conferir os resultados obtidos.
Sistematização do conceito da aula

Tempo sugerido: 3min
Orientação: Discuta com a turma sobre as atividades desenvolvidas e sobre o aprendizado adquirido. Formalize nesta etapa a soma e subtração de decimais de forma sistemática, a fim de que o aluno possa usar este conhecimento de forma geral. Se possível utilize um quadro para realizar estes exemplos.
Propósito: Sistematizar de forma clara o conceito adquirido.
Discuta com a Turma: Pergunte a turma sobre as dúvidas ou dificuldades encontradas para utilizar tal conceito.
Sistematização do conceito da aula

Tempo sugerido: 3min
Orientação: Discuta com a turma sobre as atividades desenvolvidas e sobre o aprendizado adquirido. Formalize nesta etapa a soma e subtração de decimais de forma sistemática, a fim de que o aluno possa usar este conhecimento de forma geral. Se possível utilize um quadro para realizar estes exemplos.
Propósito: Sistematizar de forma clara o conceito adquirido.
Discuta com a Turma: Pergunte a turma sobre as dúvidas ou dificuldades encontradas para utilizar tal conceito.
Encerramento

Tempo sugerido: 2 minutos.
Orientação: Discuta com a turma sobre as atividades desenvolvidas e sobre o aprendizado adquirido.
Propósito: Concluir a aula, fazer uma revisão do que foi aprendido e das atividades desenvolvidas.
Discuta com a turma: Tome conhecimento da opinião dos alunos sobre a aula e sobre as atividades e de como elas impactaram na aquisição de conhecimento do aluno sobre o tema em questão.
Raio X

Tempo sugerido: 5 minutos.
Orientações: Peça que, individualmente, os alunos leiam a atividade e a realizem, utilizando as fichas. Em seguida, faça um levantamento dos resultados obtidos e discuta as estratégias de resolução.
Utilize o guia de intervenções para discutir com os alunos as formas e possibilidades de respostas.
Propósito: Verificar o conhecimento adquirido em relação a multiplicação e divisão de decimais.
Materiais complementares para impressão:
Para o aluno
Para o professor
Sugestão de adaptação para ensino remoto
Código do plano
MAT6_06NUM02
Recursos
- Necessários: Caderno, lápis, borracha, grupo de WhatsApp ou acesso à plataforma de interação combinada entre professor e alunos
- Opcionais: Khan Academy https://pt.khanacademy.org/math/arithmetic/arith-decimals/arith-review-sub-decimals/v/subtracting-decimals-up-to-thousandths-place
Para este plano, foque na etapa Atividade Principal e Raio X.
Atividade Principal
Professor, inicie essa aula organizando os alunos em quartetos. Explique a eles que deverão fazer uma videochamada de grupo pelo WhatsApp e que eles terão cerca de 10 minutos para fazer a atividade proposta. Combine com eles o horário de retorno ao grande grupo, para que possam compartilhar suas conclusões. Compartilhe com eles o primeiro e o segundo slides da Atividade Principal. Ao retornarem para o grande grupo, explore bem esse momento. Garanta que cada grupo consiga compartilhar suas conclusões. Se sua aula for síncrona, peça aos alunos de cada grupo que acionem seus microfones para explicar suas estratégias. Caso contrário, solicite que enviem um áudio para o grande grupo explicando suas conclusões. Posteriormente, envie um áudio com a devolutiva dessa atividade.
Discussão das soluções
A discussão das soluções é uma etapa importantíssima da aula. É o momento de justificar as estratégias e respostas usadas para a resolução do problema proposto na atividade principal. Antes de compartilhar o slide da Discussão das soluções com os alunos, explore as perguntas do terceiro slide da Atividade Principal. Essas perguntas ajudarão os alunos a analisar os números para respondê-las. Em seguida, compartilhe o primeiro slide da Discussão das soluções e peça a eles que comparem com as suas próprias conclusões. Estimule os alunos a usarem uma ferramenta de áudio ou vídeo para falarem como pensaram para atender o que foi solicitado e o que acham das colocações dos personagens no slide. Pergunte se eles pensaram da mesma forma e, caso contrário, peça que compartilhem suas estratégias. Estimule os alunos a perceberem que podemos seguir por diversos caminhos para chegar a uma solução e que o erro faz parte do processo de aprendizagem. Assim, você estará combatendo a valorização excessiva da resposta certa. Lembre-se que o objetivo da aula é que os alunos compreendam a adição e a subtração de números decimais. Sendo assim, explore essa atividade para que eles possam perceber a necessidade da comparação entre os números, bem como de observar as posições decimais para realizar as operações. Use as situações propostas no quarto slide da Discussão de soluções para explorar a subtração.
Raio X
Compartilhe o slide do Raio X com os alunos. Dê a eles você pode reuni-los em grupos novamente para que realizem a proposta ou organizar um fórum para que eles possam compartilhar suas conclusões. Caso sua aula não seja síncrona, dê uns dias para eles fazerem a atividade e posteriormente grave um áudio ou um podcast com uma devolutiva dessa atividade e envie para os alunos.
Convite às famílias
A participação das famílias no processo de aprendizagem é de grande importância para o aluno. Porém, ressaltamos que os pais não são professores de matemática e muitos podem estar ocupados com outras funções em casa ou mesmo trabalhando. Portanto, indicamos a participação das famílias no compartilhamento e discussão de possíveis soluções para os problemas propostos ou interagindo com o aluno em alguma atividade específica. Sugerimos que os alunos convidem seus familiares para assistir ao vídeo sobre adição e subtração do Khan Academy https://pt.khanacademy.org/math/arithmetic/arith-decimals/arith-review-sub-decimals/v/subtracting-decimals-up-to-thousandths-place
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Kurth Correa Waldhelm
Mentora: Débora Vieira de Moraes
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF06MA10 - Resolver e elaborar problemas com números racionais positivos na representação decimal, envolvendo as quatro operações fundamentais e potenciação, por meio de estratégias diversas, utilizando estimativas e arredondamentos para verificar a razoabilidade de respostas, com e sem o uso de calculadora.
Objetivos específicos
Conceituar, resolver e elaborar estratégias de cálculo para adição e subtração de números positivos na forma decimal.
Conceito-chave
Adição e subtração de decimais.
Recursos necessários
- Folha de papel A4 branca;
- Atividades impressas em folhas, coladas no caderno ou não;
- Calculadora ou celular (se possível).















