Resumo da Aula
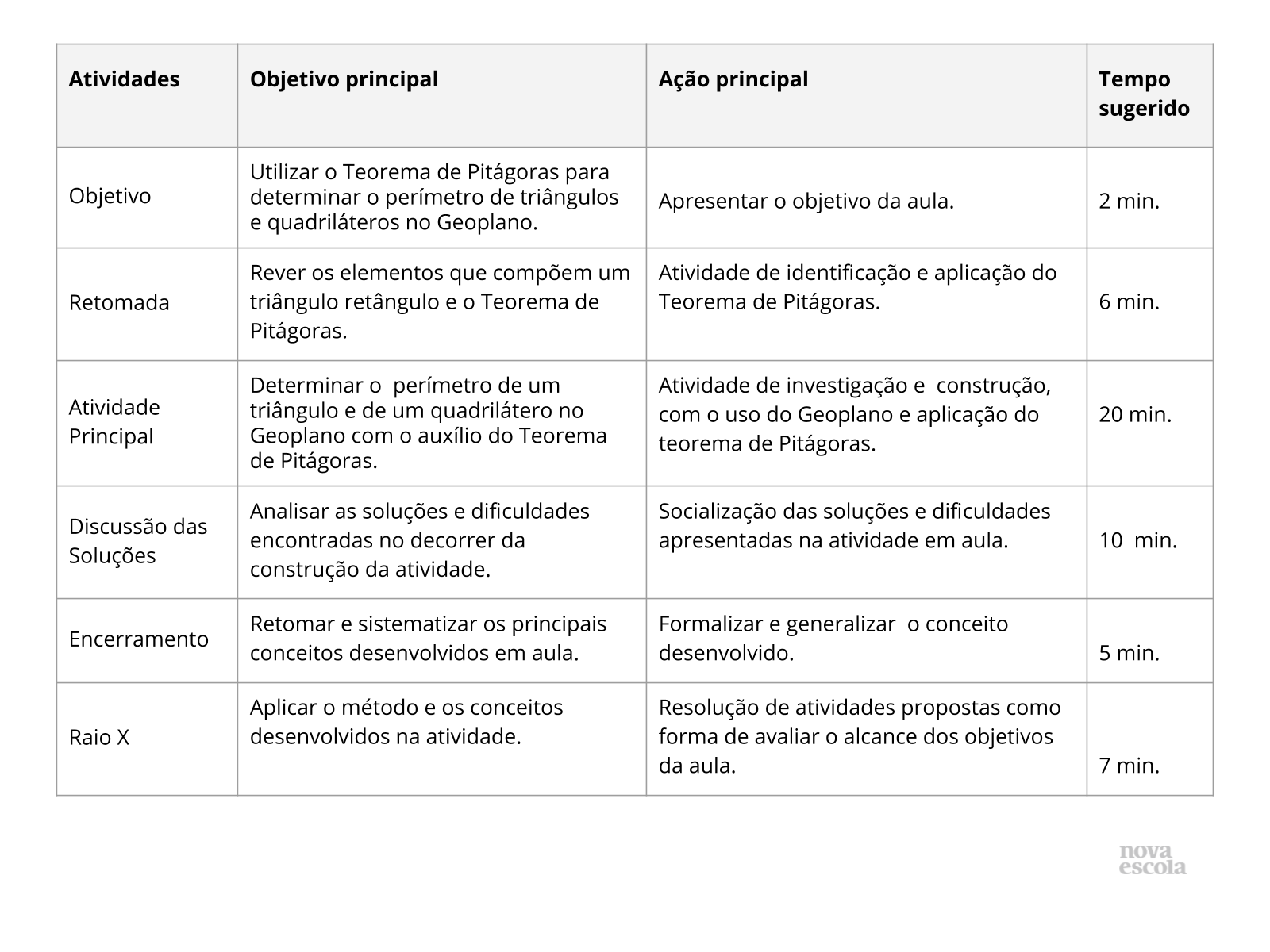
Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “
Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientações: Apresente o objetivo da aula de forma clara, de modo que os alunos percebam o que se deseja alcançar com as atividades a serem desenvolvidas na aula.
Propósito: Apresentar o objetivo da aula.
Discuta com a turma:
- Como se chama cada lado do triângulo retângulo?
- O que nos diz o Teorema de Pitágoras?
Retomada
Tempo sugerido: 6 minutos.
Orientações:
Realize a atividade em duplas. Disponibilize a atividade impressa para cada dupla.
Propósito: Rever conceitos relacionados aos lados de um triângulo retângulo e a aplicação do teorema de Pitágoras. Rever o conceito de quadrilátero.
Discuta com a turma:
- Quantos triângulos vocês veem na figura?
- Quando um triângulo é retângulo?
- Como se relacionam as medidas dos lados de um triângulo retângulo, segundo o Teorema de Pitágoras?
- Quais as características de um quadrilátero?
- O que representa o perímetro de uma figura plana?
Materiais complementares para impressão:
Aquecimento
Resolução do Aquecimento
Atividade Principal
Tempo sugerido: 20 minutos. (slides 4, 5 e 6).
Orientações:
Desenvolva a atividade em equipes de 3 alunos. Disponibilize os geoplanos e a atividade impressa para os alunos. As distâncias entre os pinos do geoplano devem ser de exatamente 01 cm. Oriente os alunos a adotarem uma casa decimal nas medições com a régua, realizando, se necessário, arredondamentos segundo as regras padrão. As medições devem ser feitas a partir do centro dos pinos.
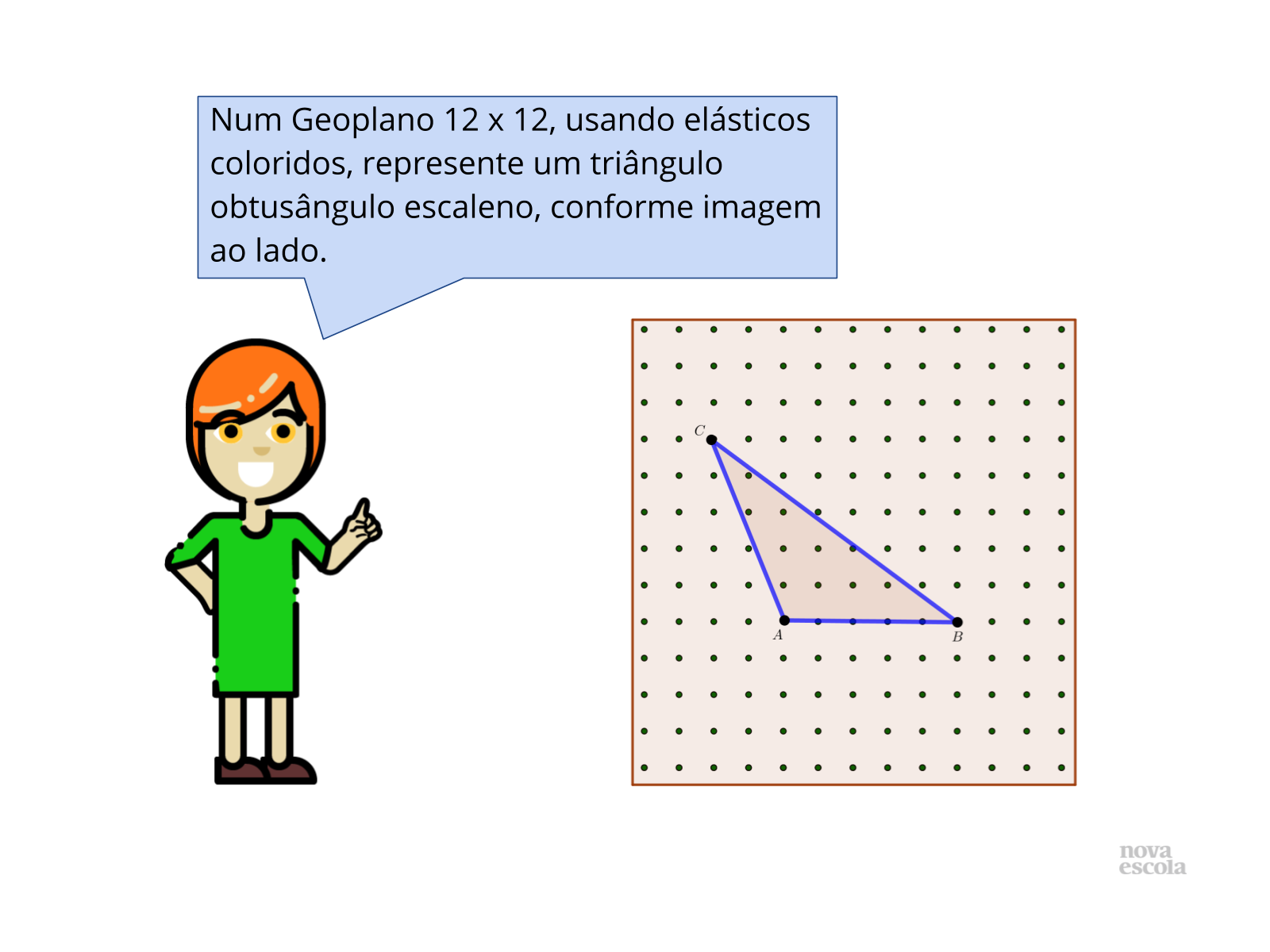
Propósito: Aplicar o teorema de Pitágoras no geoplano, para determinar o perímetro de um triângulo obtusângulo escaleno.
Discuta com a turma:
- Quando um triângulo é obtusângulo?
- O que representa o perímetro de um polígono?
- Há necessidade de construir um triângulo retângulo para auxiliar na determinação da medida do segmento AB ?
Materiais complementares para impressão:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Atividade Principal

Tempo sugerido: 20 minutos. (slides 4, 5 e 6).
Orientações:
Observe se as medições com a régua estão sendo feitas corretamente, oriente que as mesmas devem ser feitas a partir dos centros dos pinos e adotando valores aproximados para o resultado com uma casa decimal, utilizando, se necessário as regras de arredondamentos.
Propósito: Aplicar o teorema de Pitágoras no geoplano para determinar o perímetro de um triângulo obtusângulo escaleno.
Discuta com a turma:
- Qual dos lados de um triângulo retângulo é chamado de hipotenusa?
- Quando cruzamos uma reta horizontal com outra vertical, qual o ângulo formado entre elas?
- Qual a medida do ângulo oposto a hipotenusa em um triângulo retângulo?
- O que é o perímetro de um triângulo?
Atividade Principal
Tempo sugerido: 20 minutos. (slides 4, 5 e 6).
Orientações:
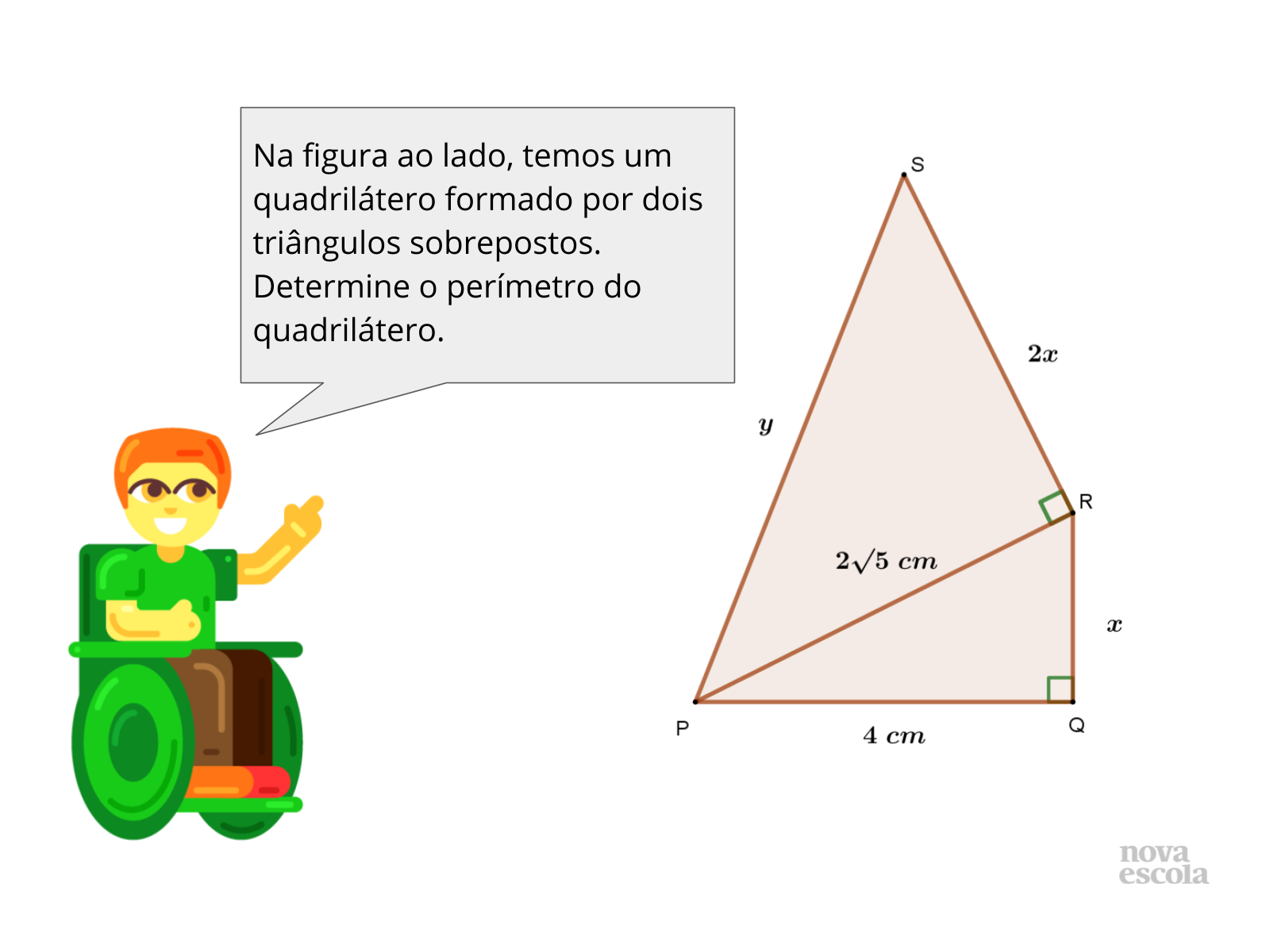
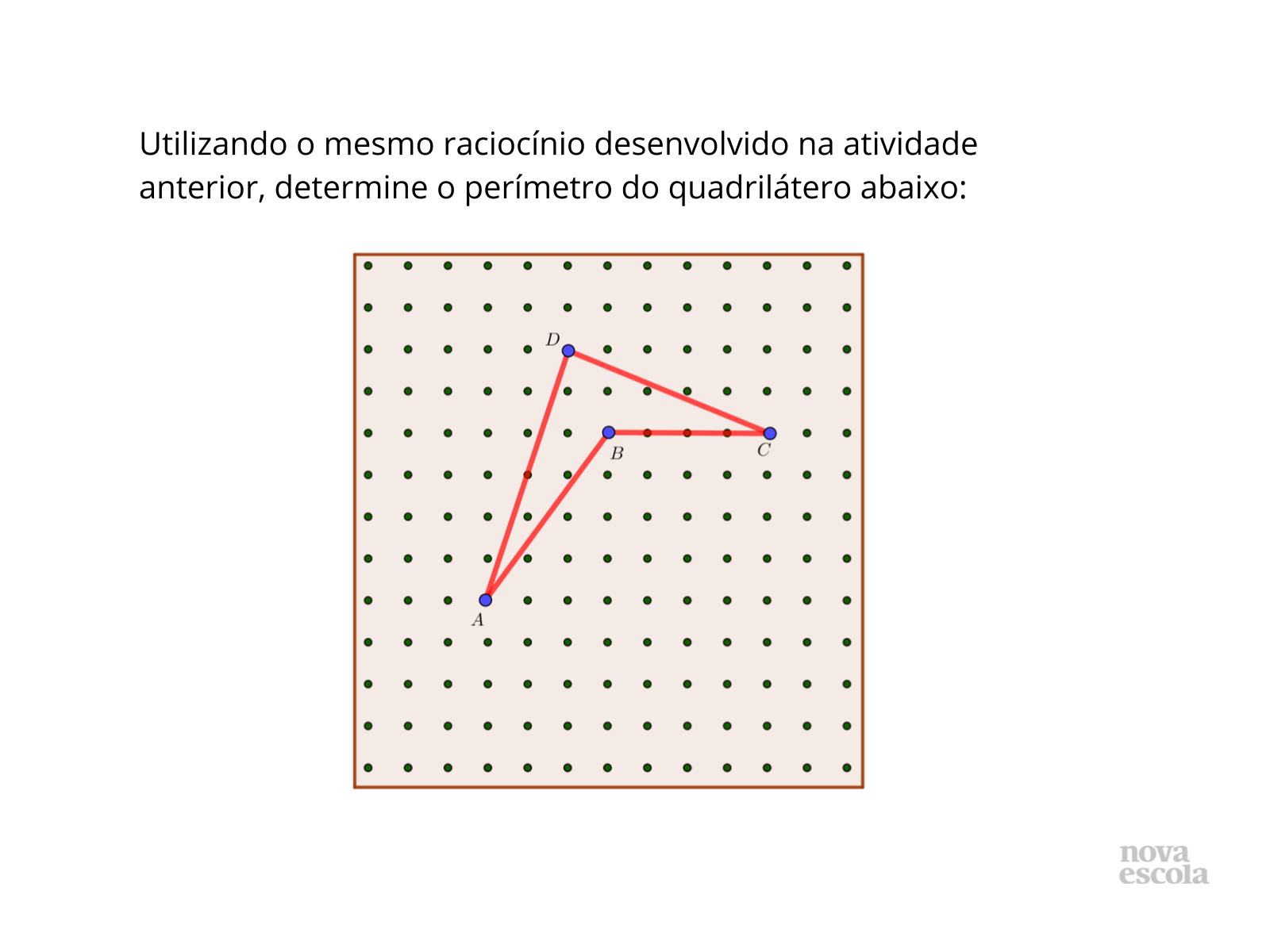
Não há necessidade de usar a régua e efetuar medições, o que se espera é que os alunos apliquem diretamente o teorema de Pitágoras e obtenha o perímetro através de uma soma de números irracionais.
Propósito: Aplicar o teorema de Pitágoras no geoplano para determinar o perímetro de um quadrilátero não regular.
Discuta com a turma:
- Por um mesmo segmento qualquer do quadrilátero, quantos triângulos retângulos podemos obter, tendo-o como hipotenusa?
- Há necessidade de construir um triângulo retângulo para auxiliar na determinação da medida do segmento BC?
Atividade Principal
Tempo sugerido: 10 minutos. (slides 7 e 8).
Orientações:
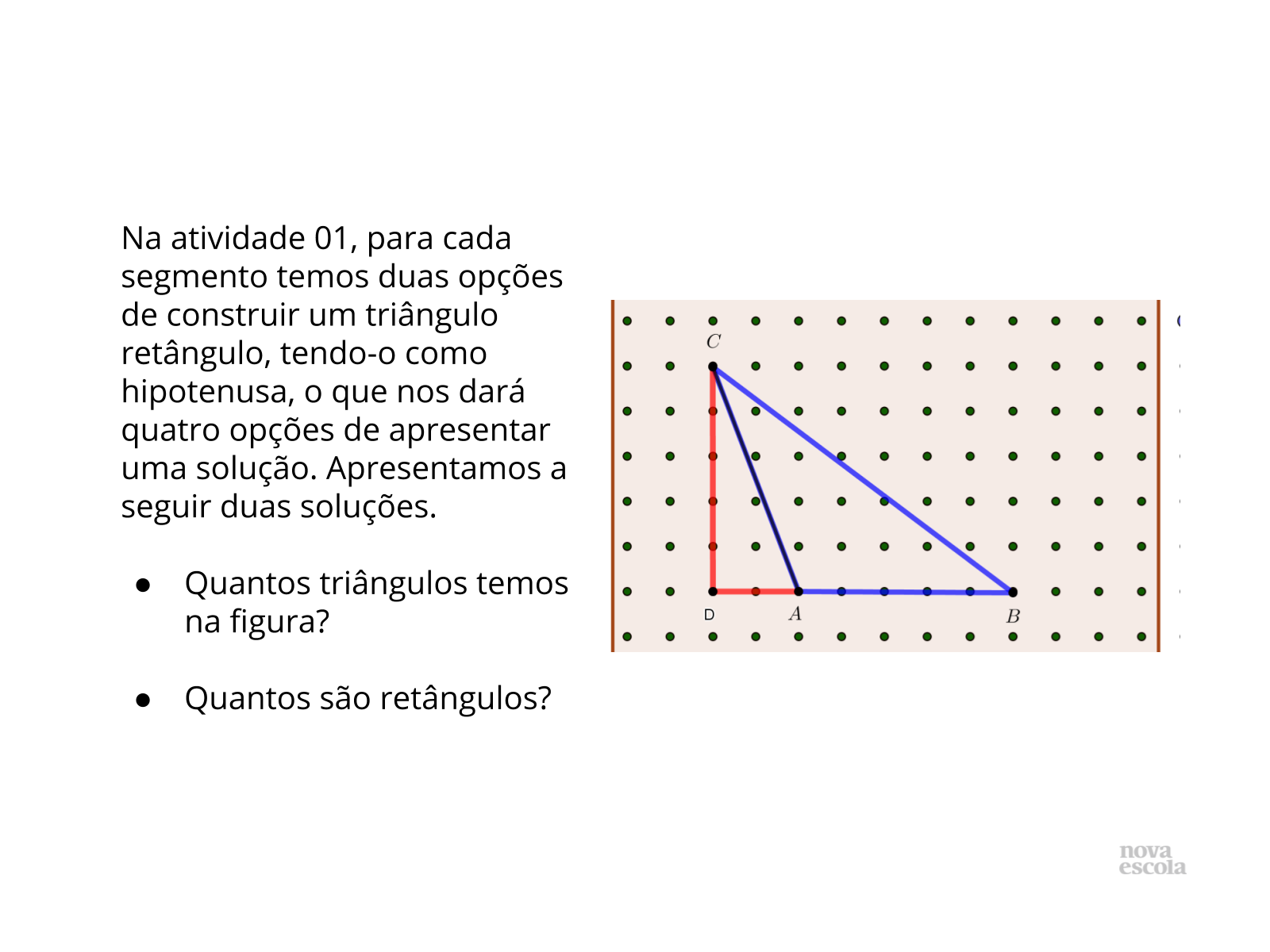
Apresente a discussão da Atividade Principal, uma vez que a mesma fundamenta a resolução da Segunda atividade. Apresente duas, das quatro imagem possíveis, pois acredita-se que a resolução ficará em torno das mesmas. No entanto, caso alguma equipe apresente uma outra, se faz necessário ao professor incluí-la na discussão. Do contrário, poderá estimular os alunos somente a identificarem.
Propósito: Discutir a solução e as dificuldades apresentadas no decorrer da atividade.
Discuta com a turma:
- Quantos triângulos retângulos podemos construir tendo um dos segmentos não horizontal do triângulo ABC, como hipotenusa?
- Alguma equipe apresentou tal solução?
Atividade Principal
Tempo sugerido: 10 minutos. (slides 7 e 8).
Orientações:
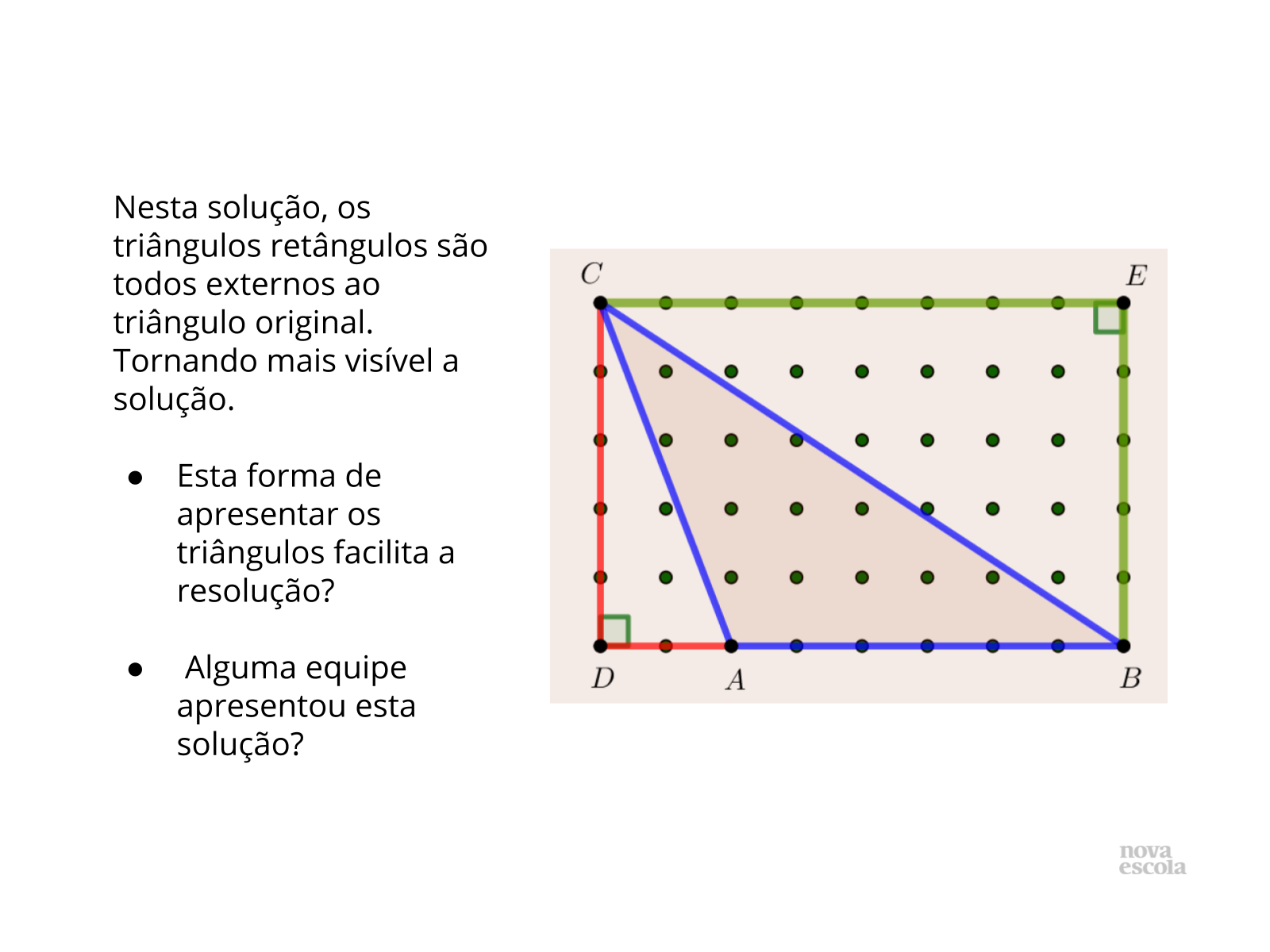
Apresente a discussão da Atividade Principal, uma vez que a mesma fundamenta a resolução da Segunda atividade. Apresente duas, das quatro imagem possíveis, pois acredita-se que a resolução ficará em torno das mesmas. No entanto, caso alguma equipe apresente uma outra, se faz necessário ao professor incluí-la na discussão. Do contrário, poderá estimular os alunos somente a identificarem.
Propósito: Discutir a solução e as dificuldades apresentadas no decorrer da atividade.
Discuta com a turma:
- Essa solução é mais viável que a anterior?
- Alguma equipe apresentou tal solução?
- Alguma equipe apresentou solução diferente das apresentadas?
- Alguém pode descrever uma solução diferente das anteriores?
Encerramento
Tempo sugerido: 5 minutos.
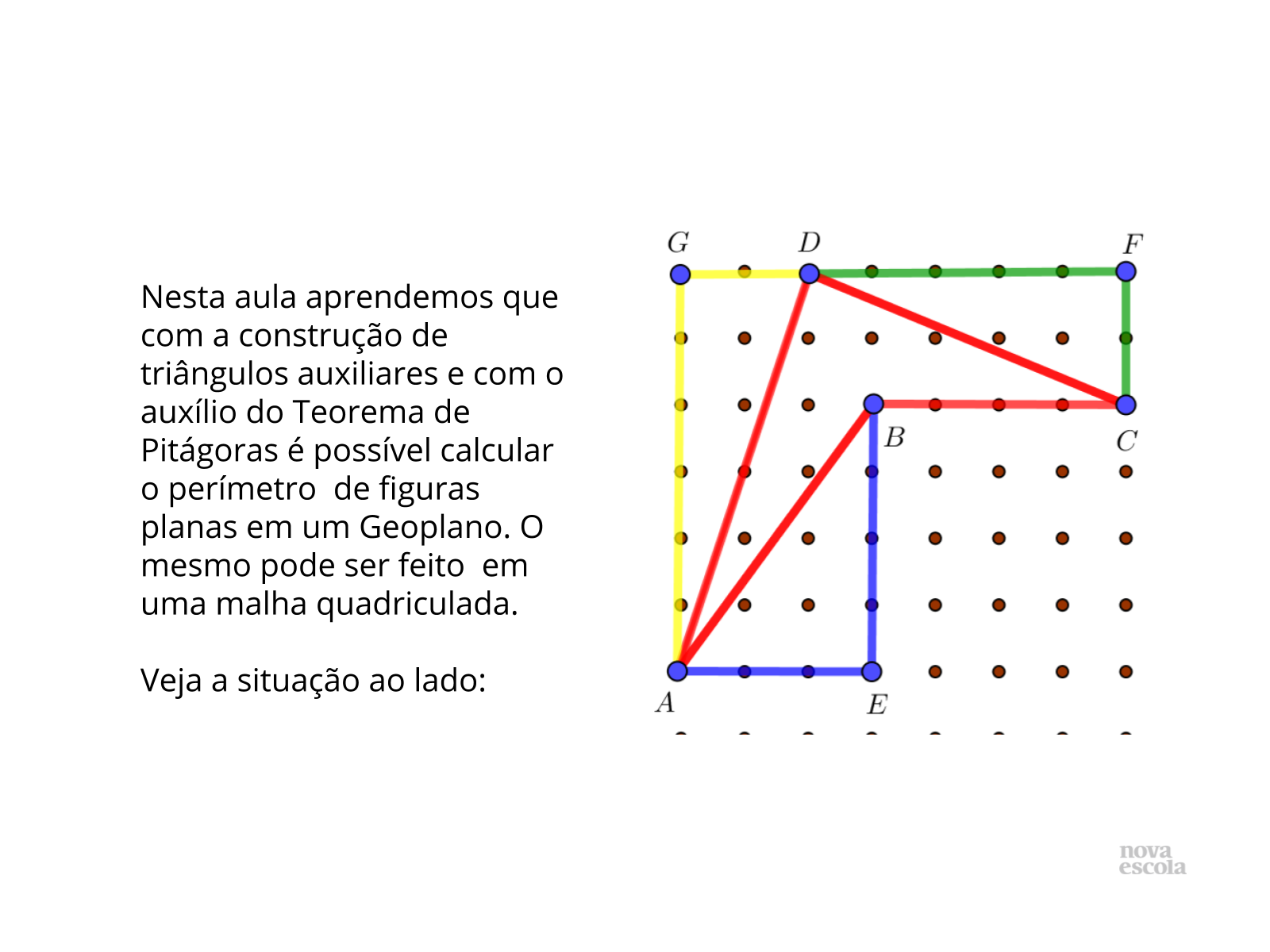
Orientações: Comente de forma geral a solução apresentada no slide para o cálculo do perímetro do quadrilátero ABCD apresentado, destacando cada triângulo auxiliar. Não precisa efetuar os cálculos, somente enfatize a aplicabilidade do teorema de Pitágoras em tal solução.
Propósito: Sintetizar o que foi desenvolvido na aula.
Discuta com a turma:
- Qual a medida dos catetos do triângulo em amarelo?
- Como calcular a medida do segmento AD?
Raio X
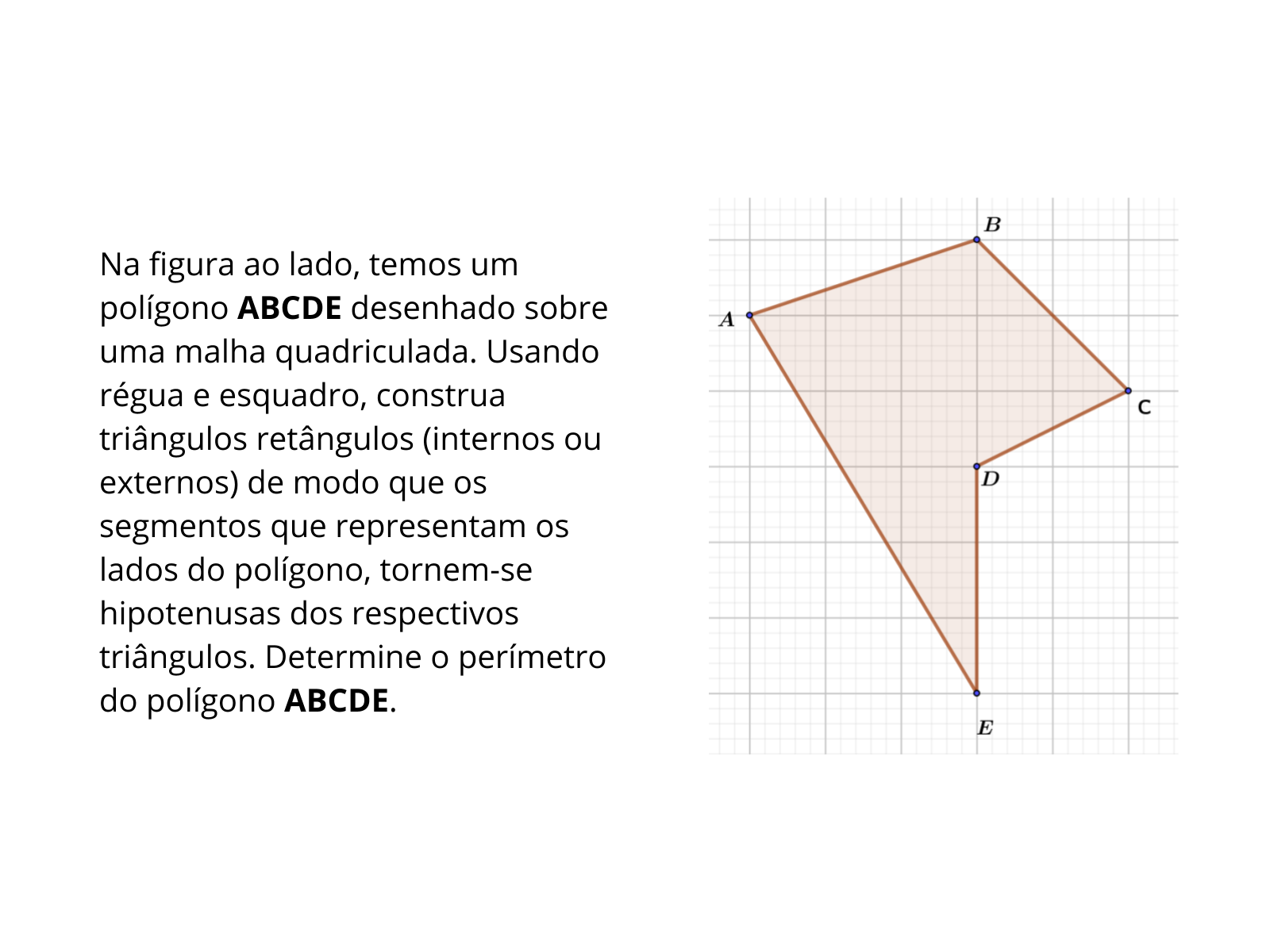
Tempo sugerido: 7 minutos.
Orientações:
Disponibilize a atividade impressa para os alunos. Realize tal atividade individual, observando o alcance dos objetivos da aula.
Propósito: Avaliar se os objetivos da aula foram alcançados
Discussão com a turma:
- Qual o ângulo entre duas retas não paralelas da malha quadriculada?
- Quantos triângulos retângulos podemos construir, de modo que o segmento AE seja a hipotenusa?
Materiais complementares para impressão:
Raio X
Resolução do raio x
Atividade complementar
Resolução da atividade complementar
 Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.