Resumo da Aula
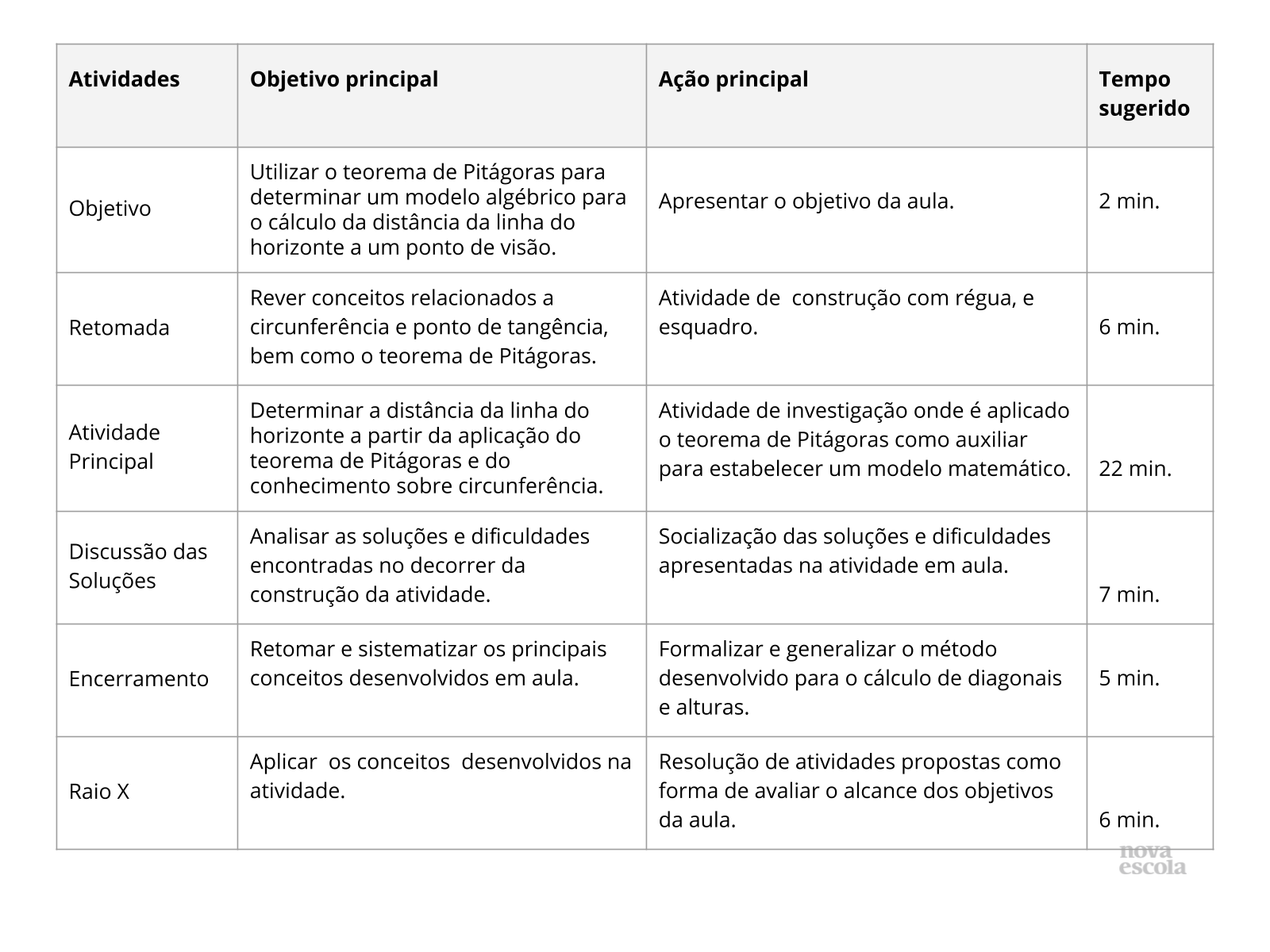
Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientações:
Apresente o objetivo da aula de forma clara, de modo que os alunos percebam o que se deseja alcançar com as atividades a serem desenvolvidas na aula.
Propósito: Apresentar o objetivo da aula.
Discuta com a turma:
- O que representa a linha do horizonte?
Retomada
Tempo sugerido: 6 minutos. (slides 3 e 4) .
Orientações: Disponibilize o material impresso para os alunos. Realize a atividade em duplas.
Propósito: Rever conceitos relacionados a circunferência e ponto de tangência.
Materiais complementares para impressão:
Aquecimento
Resolução do Aquecimento
Retomada

Tempo sugerido: 6 minutos. (slides 3 e 4) .
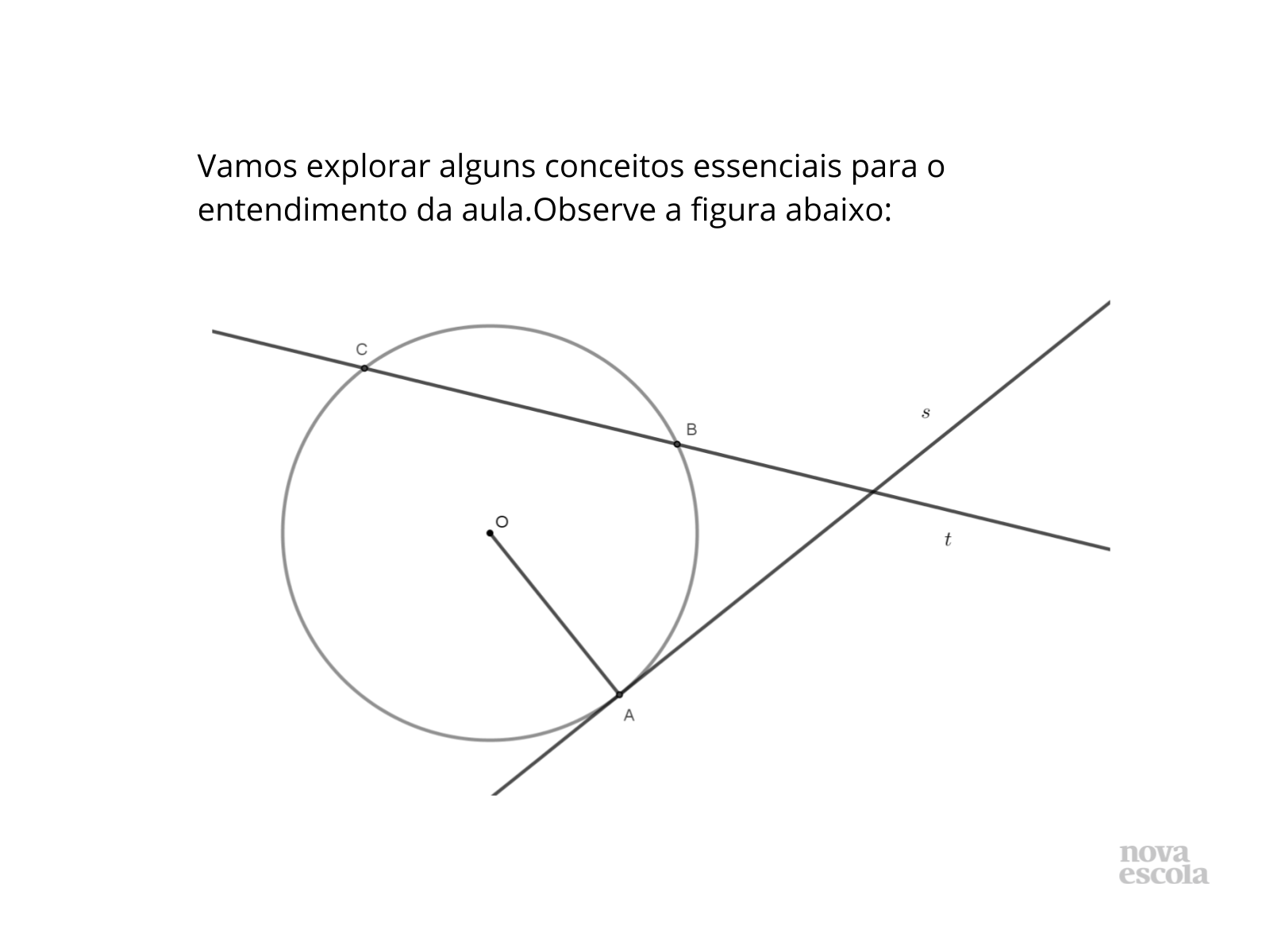
Orientações: Trabalhe de forma comparativa os conceitos de reta tangente e secante. Oriente os alunos quanto a importância do traçado correto da reta tangente e sua influência na medida do ângulo entre a mesma e o raio, no ponto de tangência.
Propósito: Rever conceitos relacionados a circunferência e ponto de tangência.
Discuta com a turma:
- Quando uma reta é tangente a uma circunferência?
- Qual a diferença fundamental entre reta secante e reta tangente?
- Qual a medida do ângulo formado entre o raio OA e a reta tangente em A ?
Atividade Principal

Tempo sugerido: 22 minutos. (slides 5, 6, 7 e 8).
Orientações:
Realize a atividade em equipes de no máximo 3 componentes. Disponibilize a atividade impressa para as equipes. Os alunos deverão ler atentamente as informações no texto para que possam compreender as etapas da atividade e seu significado no contexto.
Propósito: Determinar a distância da linha do horizonte a partir da aplicação do teorema de Pitágoras e do conhecimento sobre circunferência.
Materiais complementares para impressão:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Atividade Principal

Tempo sugerido: 22 minutos. (slides 5, 6, 7 e 8).
Orientações:
Realize a atividade em equipes de no máximo 3 componentes. Disponibilize a atividade impressa para as equipes. Os alunos deverão ler atentamente as informações no texto para que possam compreender as etapas da atividade e seu significado no contexto.
Propósito: Determinar a distância da linha do horizonte a partir da aplicação do teorema de Pitágoras e do conhecimento sobre circunferência.
Discuta com a turma:
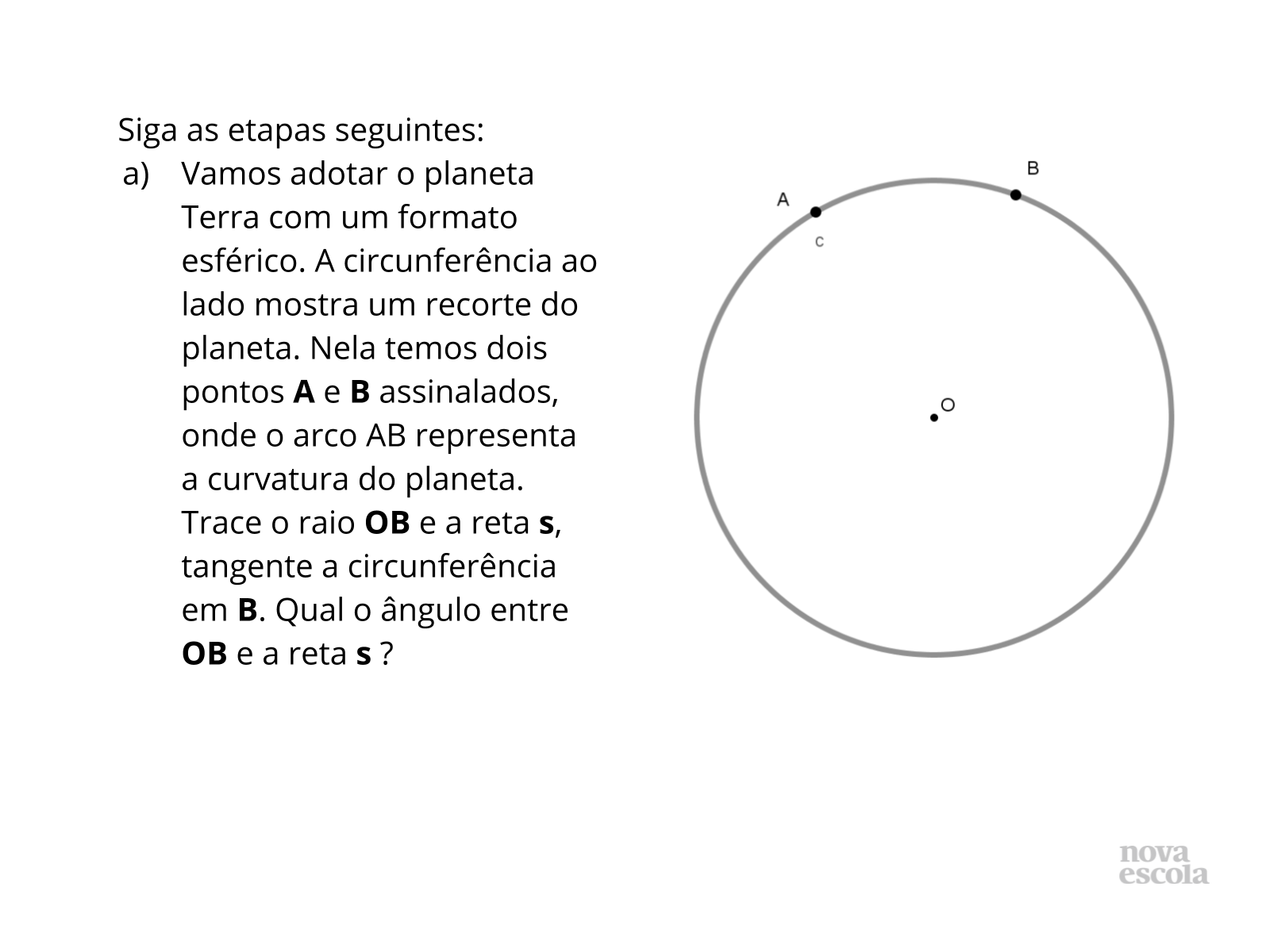
- Qual o formato do planeta Terra?
- A distância que uma pessoa percebe a linha do horizonte é a mesma de uma outra mais baixa?
Atividade Principal
Tempo sugerido: 22 minutos. (slides 5, 6, 7 e 8).
Orientações:
Realize a atividade em equipes de no máximo 3 componentes. Disponibilize a atividade impressa para as equipes. Os alunos deverão ler atentamente as informações no texto para que possam compreender as etapas da atividade e seu significado no contexto.
Propósito: Determinar a distância da linha do horizonte a partir da aplicação do teorema de Pitágoras e do conhecimento sobre circunferência.
Discuta com a turma:
- O triângulo ABO é retângulo?
- Qual a medida do ângulo formado pelo raio e reta tangente?
- Qual a relação entre a reta s e a linha do horizonte?
Atividade Principal

Tempo sugerido: 22 minutos. (slides 5, 6, 7 e 8).
Orientações:
Realize a atividade em equipes de no máximo 3 componentes. Disponibilize a atividade impressa para as equipes. Os alunos deverão ler atentamente as informações no texto para que possam compreender as etapas da atividade e seu significado no contexto.
Propósito: Determinar a distância da linha do horizonte a partir da aplicação do teorema de Pitágoras e do conhecimento sobre circunferência.
Discuta com a turma:
- Qual a medida do ângulo formado pelo raio e a reta tangente?
- O triângulo HBO é retângulo?
- O que representa, no contexto explorado, o ponto de tangência B, da reta s com a circunferência?
- O que o segmento AH representa na realidade?
- O que o segmento AB representa na realidade?
- Como se faz o arredondamento de um número decimal?
Discussão das Soluções

Tempo sugerido: 7 minutos. (slides 9 e 10).
Orientações: É importante que os alunos percebam que o teorema de Pitágoras é um instrumento auxiliar e que o modelo deduzido pode ser aplicado de forma direta, mas sempre considerando alturas ao nível do mar.
Propósito: Discutir a solução e as dificuldades apresentadas no decorrer da atividade
Discuta com a turma:
- Qual a forma do planeta Terra?
- Quais os elementos variáveis em tal modelo?
Discussão das Soluções

Tempo sugerido: 7 minutos. (slides 9 e 10).
Orientações: É importante mostrar a influência que o uso de valores arredondados apresentam em alguns resultados matemáticos e a importância de usar os valores mais próximos da realidade possível.
Propósito: Discutir a solução e as dificuldades apresentadas no decorrer da atividade
Discuta com a turma:
- Usar valores aproximados pode influenciar em resultados de forma significativa?
Discussão das Soluções
Tempo sugerido: 5 minutos.
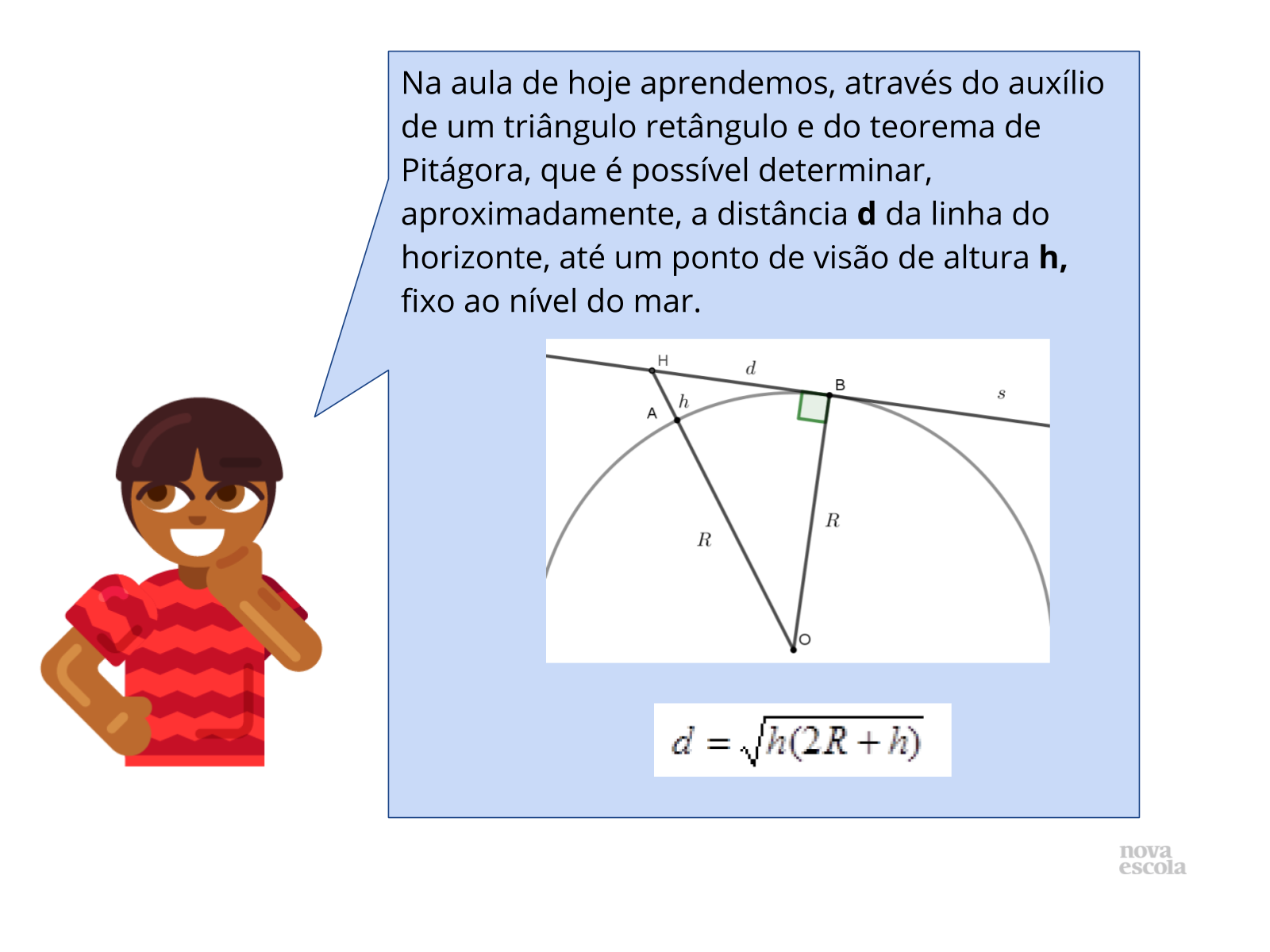
Orientações: Encerre sintetizando o conceito construído em aula, busque mostrar de forma breve as relações que dão origem ao modelo, ressaltando a importância do teorema de Pitágoras em tal evento.
Propósito: Sintetizar o que foi desenvolvido na aula.
Discuta com a turma:
- O modelo desenvolvido será sempre válido?
- Caso você esqueça do modelo desenvolvido, o que é necessário para calcular a distância da linha do horizonte, ao nível do mar?
- Você conhece alguma outra aplicação do teorema de Pitágoras?
Raio X
Tempo sugerido: 6 minutos.
Orientações:
O Raio X deve ser realizado individualmente. As perguntas produtivas (Discuta com a turma) podem ajudar os alunos a construírem um roteiro de resolução.
Propósito: Avaliar se os objetivos da aula foram alcançados.
Discussão com a turma:
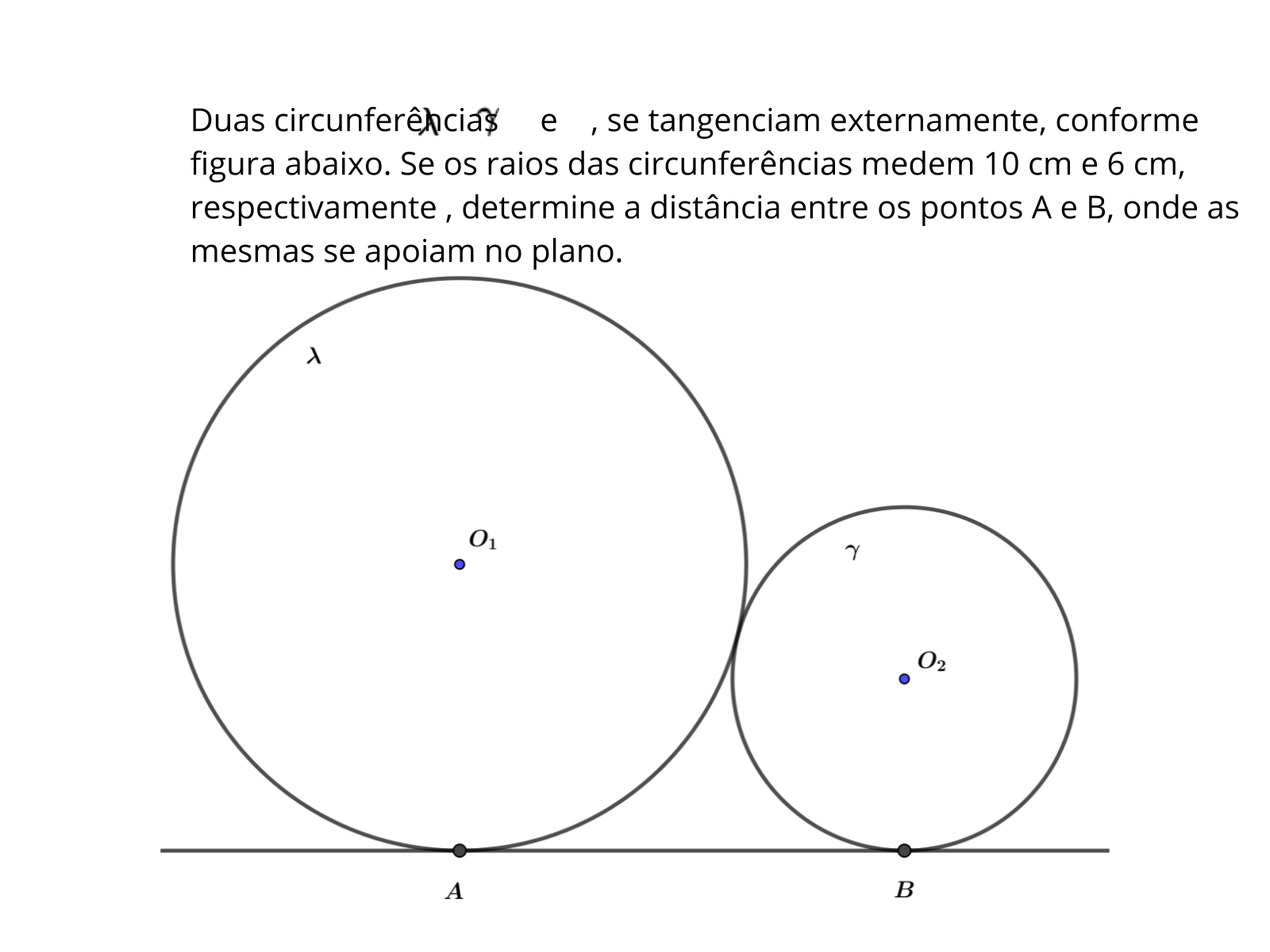
- Os centros das circunferências estão alinhados com o ponto de tangência? O que garante tal fato?
- Qual a distância entre os centros das circunferências e os respectivos pontos de tangência com o plano?
- A distância entre os centros é maior ou menor que a distância entre os pontos A e B?
Materiais complementares para impressão:
Raio X
Resolução do raio x
Atividade complementar
Resolução da atividade complementar
 Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.