Resumo da Aula
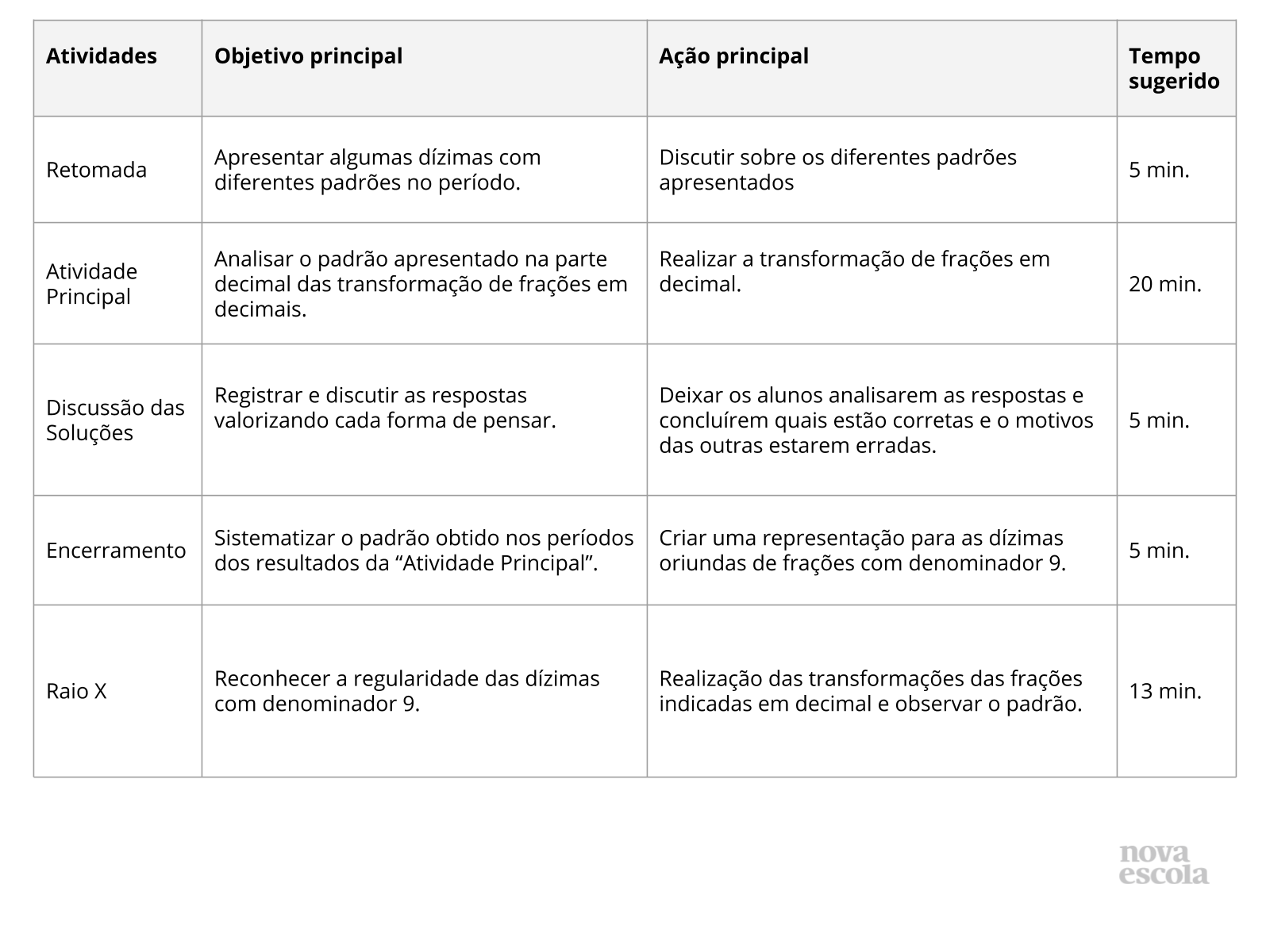
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientações: Projete, escreva no quadro ou leia o objetivo para turma.
Propósito: Apresentar o objetivo à classe
Retomada

Tempo sugerido: 5 minutos.
Orientações: Peça aos alunos que testem várias frações antes para ter certeza que são dízimas e não decimais exatos. Caso o tempo seja pouco, não use as quatro frações, use apenas duas (uma dízima simples e outra composta).
Propósito: Recordar as dízimas periódicas e seus períodos.
Discuta com a Turma:
- Quando uma dízima é considerada simples ou composta? Por quê?
- Questione sobre o período apresentado em cada uma. O que é possível observar?
Atividade Principal

Tempo sugerido: 20 minutos.
Orientações: Reproduza a tabela, caso necessário, ou deixe que cada grupo monte a sua. Cuidado com os arredondamentos da calculadora, é possível acontecer do último dígito visível pela calculadora ficar arredondado, nos casos em que o período é grande (formado por muitos algarismos) sua repetição pode ser vista. Peça que os alunos utilizem calculadoras com mais representações no visor, pode ser a calculadora do celular ou de algum computador.
Propósito: Fazer com que os alunos mobilizem os conhecimentos que já possuem de frações e decimais exatos para explorar o período de uma dízima periódica simples.
Atividade Principal
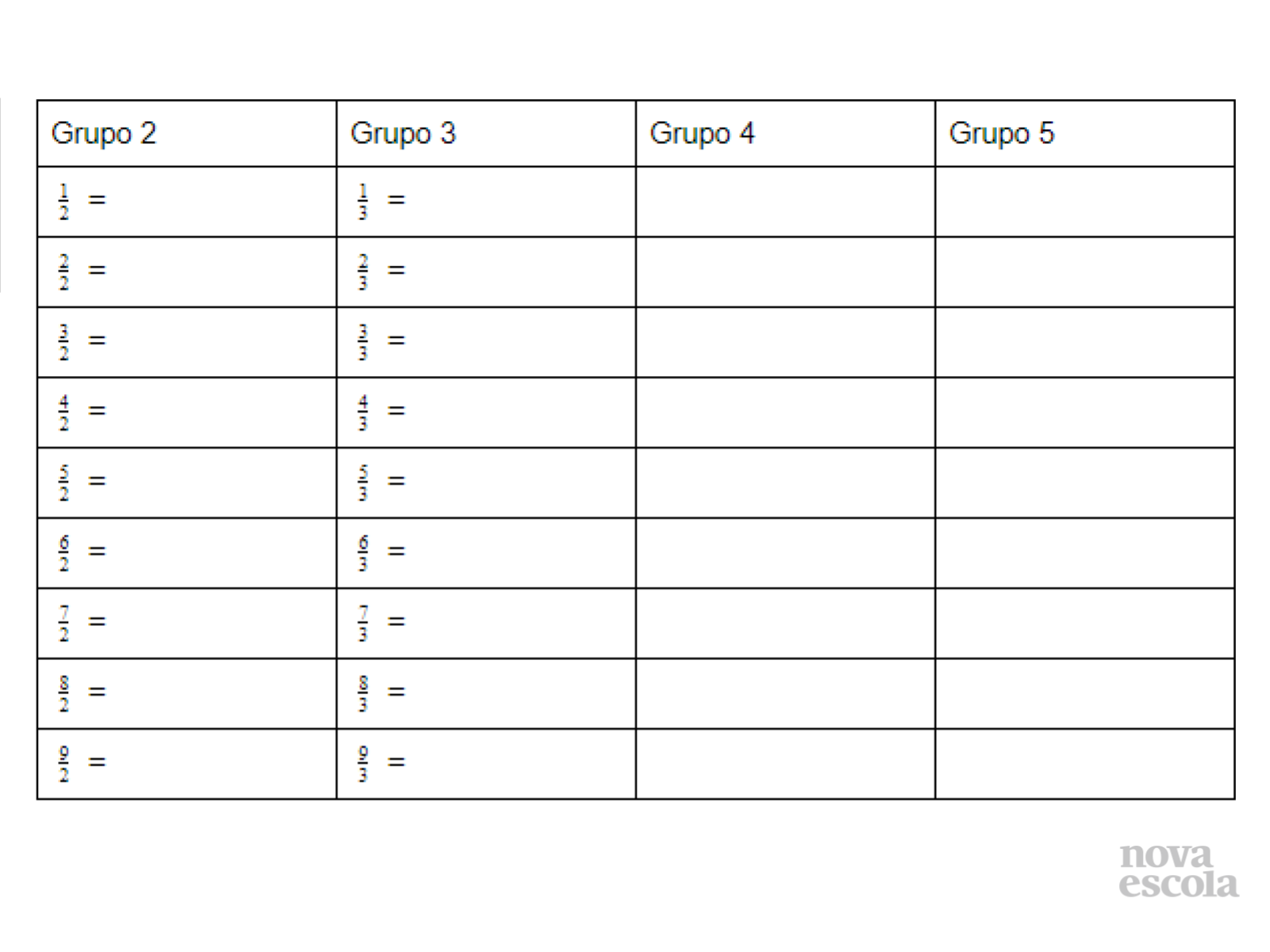
Tempo sugerido: 20 minutos.
Orientações: Fazer com que os alunos mobilizem os conhecimentos que já possuem de frações e decimais exatos para explorar o período de uma dízima periódica simples.
Atividade Principal

Tempo sugerido: 20 minutos.
Orientação: Observe que as perguntas não se aplicam a todos os grupos, se os alunos não perceberem esse padrão, faça questionamentos que despertem neles a seleção dos itens apropriados para seu grupo.
Propósito: Fazer com que os alunos mobilizem os conhecimentos que já possuem de frações e decimais exatos para explorar o período de uma dízima periódica simples.
Materiais complementares para impressão:
Atividade principal
Resolução da atividade
Guia de intervenção
Discussão das Soluções

Tempo sugerido: 5 minutos.
Orientações: Convide os alunos para apresentar suas respostas, a diversidade de soluções é bem-vinda. Caso algum aluno responda de forma incorreta, questione os outros alunos se eles concordam, se algum aluno se manifestar, deixe que ele mesmo corrija a resolução ou argumento do colega. Caso todos respondam corretamente e utilizando métodos triviais, questione de que outra forma eles poderiam chegar ao mesmo resultado.
Propósito: Discutir todas as soluções das equipes considerando a particularidade de cada uma.
Encerramento

Tempo sugerido: 5 minutos.
Orientações: Apresente o slide ou escreva no quadro o Encerramento da atividade.
Propósito: Sistematizar o conceito explorado nesta aula.
Discuta com a Turma:
- Quais foram os principais conceitos ou ideias matemáticas que você aprendeu hoje, ou que discutimos em aula hoje?
- Você ainda tem alguma dúvida? Caso você não tenha dúvida, escreva um problema semelhante e resolva-o.
- Descreva um erro ou conceito errôneo que você ou um colega apresentou na aula de hoje. O que você aprendeu com esse erro ou conceito errôneo?
- Como você ou seu grupo abordou o problema ou conjunto de problemas de hoje? Sua abordagem foi bem-sucedida? O que você aprendeu com sua abordagem?
- Descreva detalhadamente como outro aluno da turma abordou o problema. Em que aspecto tal abordagem se assemelha ou difere da maneira como você abordou o problema?
- Quais as novas palavras ou denominações foram apresentadas hoje? O que você acha que cada palavra significa? Apresente um exemplo/uma imagem de cada palavra.
- Sobre o que foi o grande debate matemático na aula de hoje? O que você aprendeu com ele?
- O que se manteve como você pensava? O que mudou?
- O que aconteceria se você mudasse algum aspecto?
- Quais foram seus pontos fortes e fracos nesta aula? Qual é o seu plano para melhorar nas áreas em que teve dificuldade?
Outra opção é deixar algumas dessas questões como tarefa de casa, podem trazer benefícios tanto quanto exercícios que exigem cálculos.
Raio X

Tempo sugerido: 13 minutos.
Orientações: A experiência feita na Atividade Principal será retomada com este Raio X, agora com o denominador 9. Questione os alunos sobre o fato de 1 = 0,999 (…). Esta é uma questão a ser discutida em outra aula, mas caso sinta que é possível, comente com os alunos sobre a ideia da representação infinita e seu significado.
Propósito: Aplicar os conceitos trabalhados na aula.
Materiais complementares para impressão:
Raio X para impressão
Resolução do Raio X
Atividade complementar
Resolução da Atividade complementar