Objetivo
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Kézia de Oliveira Silva Souza
Mentor: Ferdinando Caíque Genghini Dantas Lobo
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
[EF07MA01] Resolver e elaborar problemas envolvendo múltiplos e divisores de um número natural.
Objetivos específicos
- Resolver problemas envolvendo divisores de números naturais.
- Resolver problemas envolvendo máximo divisor comum de números naturais.
Conceito-chave
Máximo divisor comum de números naturais.
Recursos necessários
- Lápis, borracha e caderno;
- Atividades impressas em folhas, coladas no caderno ou não.
Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Aquecimento
Tempo sugerido: 5 minutos.
Orientações: Inicie a aula perguntando aos alunos se eles se lembram o que é divisor de um número, qual é a diferença entre o quadrado e o retângulo e quantos centímetros correspondem a um metro.
Propósito: Retomar alguns conceitos que serão importantes para o desenvolvimento da atividade.
Discuta com a turma:
- Você se lembra o que é divisor de um número?
- Como podemos calcular o divisor de um número natural?
- Qual é a diferença entre o quadrado e o retângulo?
- O que significa centímetro?
- Qual é a relação existente entre centímetro e metro?
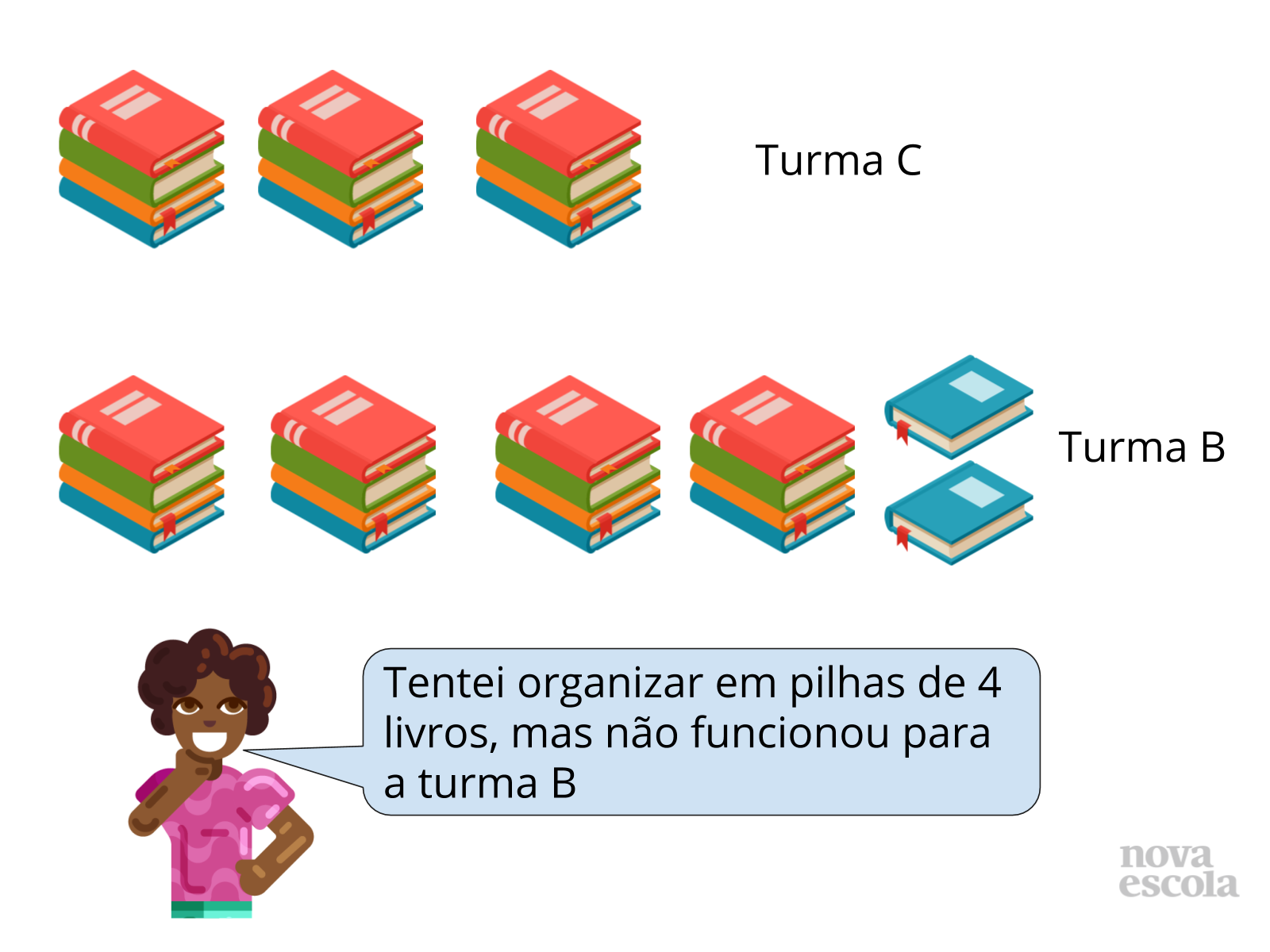
Atividade principal
Tempo sugerido: 15 minutos.
Orientações: Você poderá escrever o texto do problema no quadro, projetá-lo ou entregar uma cópia aos alunos. Peça que, em duplas, os alunos leiam a atividade e discutam a resolução do problema para ajudarem Ana.
Enquanto os alunos resolvem o problema, não faça nenhuma intervenção, apenas observe as maneiras que os alunos estão desenvolvendo a atividade, se estão desenhando, dividindo (encontrando os divisores), fatorando ou realizando outra estratégia.
Observe também, se os alunos perceberam que a sala é um retângulo, mas o piso cerâmico é um quadrado e qual unidade de medida eles estão usando.
Após os alunos realizarem a atividade, selecione três que usaram estratégias diferentes e peça que reproduzam na lousa a resolução e expliquem para os colegas como ele desenvolveu o raciocínio. A escolha dos alunos precisa ser com critério, pois conduzirá as discussões, mas a escolha não deve estar ligada apenas aos resultados corretos, e sim aos procedimentos, pois é importante discutir também os equívocos cometidos.
Propósito: Fazer com que os alunos mobilizem os conhecimentos que possuem de cálculo de divisores para concluírem qual é o maior divisor comum possível na situação proposta, o que traduz a solução do problema.
Discuta com a turma:
- Quem iniciou a atividade realizando a transformação da unidade de medida?
- Por que devemos realizar a transformação da unidade de medida?
- Ao assentar os pisos eles poderão ser divididos?
- É possível usar pisos quadrados num cômodo retangular?
- Quais seriam as possíveis medidas do lado dos pisos, se a Ana não tivesse especificado que queria a maior possível?
- Qual é a maior medida possível para o piso cerâmico?
- Por que o piso não pode ser maior que 20 cm?
Materiais complementares para impressão:
Painel de soluções
Tempo sugerido: 15 minutos (Slides 5 a 10).
Orientações: Os três alunos selecionados, que usaram estratégias diferentes ao reproduzirem na lousa a resolução, devem explicar o raciocínio usado para os colegas e assiná-la.
Propósito: Incentivar que os alunos tentem explicar como calcularam o Máximo Divisor Comum dos números propostos para responderem o problema, mesmo que ainda não conheçam esse nome, de maneira intuitiva pela interpretação do problema.
Discuta com a turma:
- Qual é a diferença das estratégias usadas?
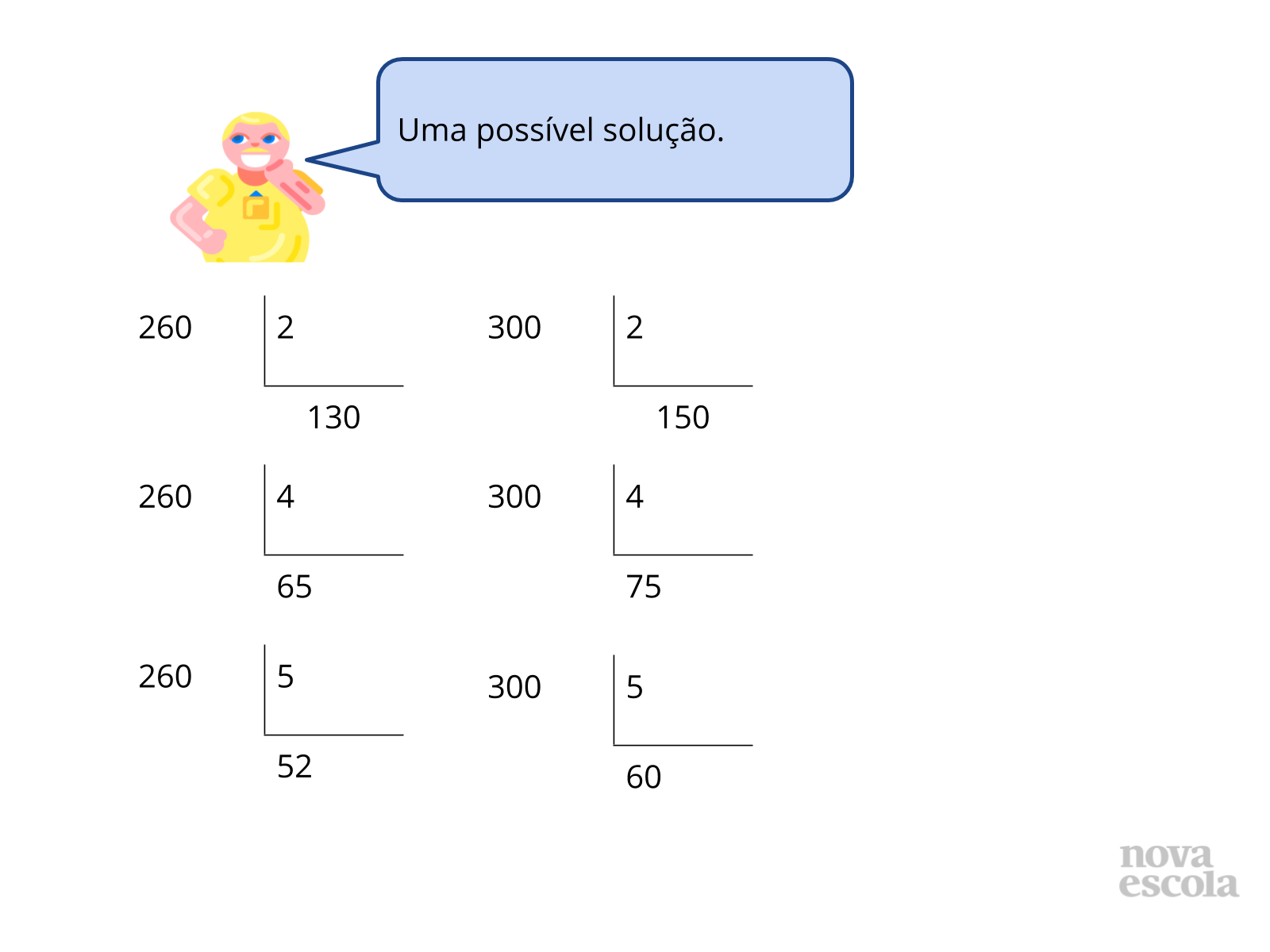
- Quais são os divisores do número 260, que representa um dos lados do retângulo (sala)?
- Quais são os divisores do número 300, que representa o outro lado do retângulo (sala)?
- Quais são os divisores dos números 260 e 300 ao mesmo tempo? Qual é o maior deles?
Na solução 1, o aluno verificou quais são os divisores de 260 e 300 ao mesmo tempo. Assim, ele descobriu quais são as possíveis medidas para o piso cerâmico. E para atender a condição da atividade, sendo o maior possível, a resposta será 20 cm.
Quando o aluno sabe os critérios de divisibilidade, agiliza a resolução da atividade. Nessa resolução, o aluno nem citou quais são os divisores, pois, a sua intenção era calcular a medida do lado do piso cerâmico que atendia a medida do lado da sala.
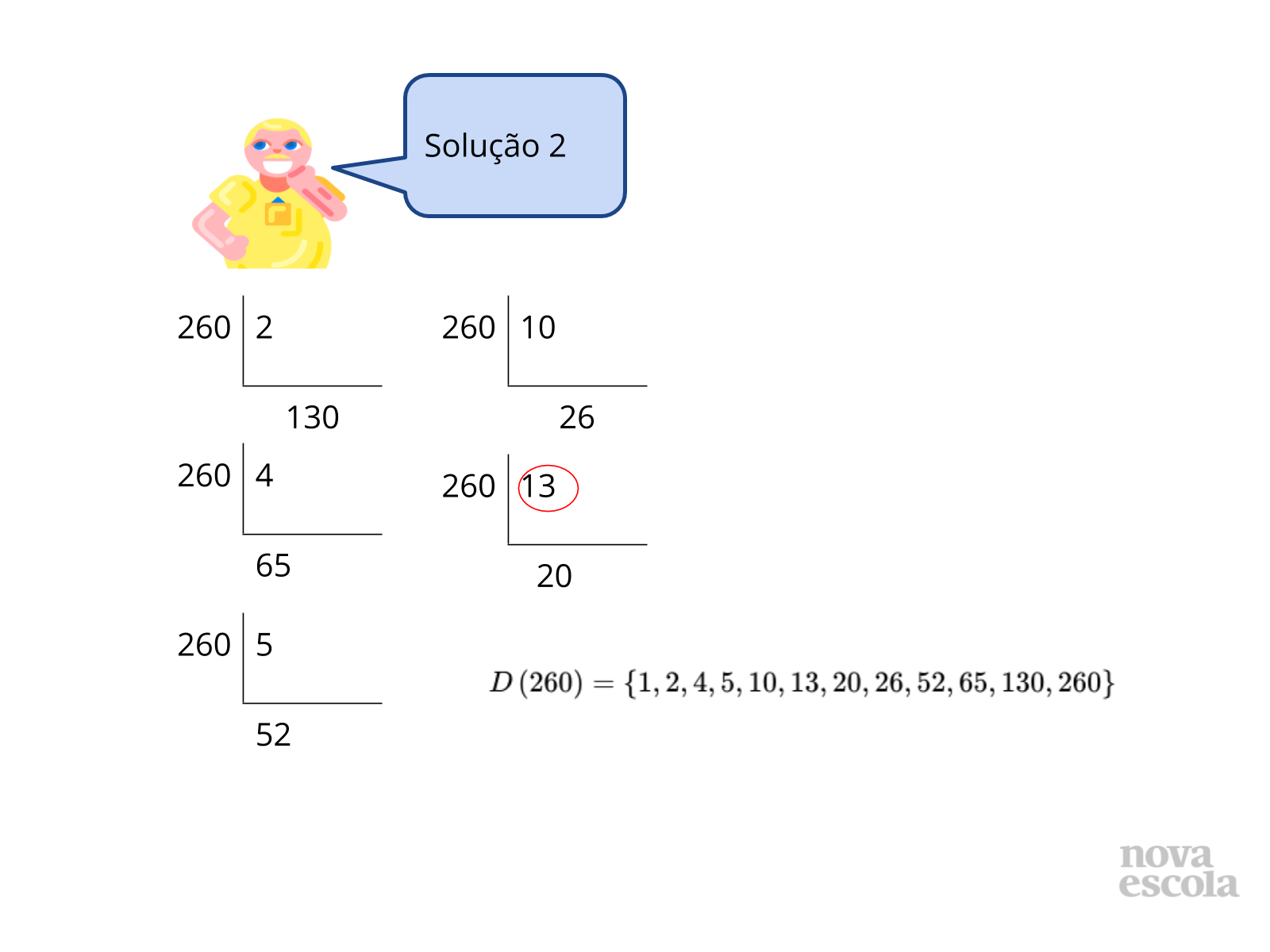
Na solução 2, o aluno calculou os divisores dos números 260 e 300 que representam as medidas dos lados da sala, depois verificou quais eram os divisores comuns e selecionou o maior (20cm) para atender o comando da atividade proposta.
Na solução 3, o aluno decompôs cada medida dos lados em fatores primos e assim verificou o que estava em comum, pois percebeu que existia essa necessidade de estar em comum para atender os dois lados da sala (260cm e 300cm). E assim, concluiu que 20 cm é a medida que satisfaz as condições solicitadas por Ana.
Os alunos obtiveram os divisores pelo processo geométrico, pelas divisões e fatorações sucessivas, mas essas não são as únicas resoluções.
Após o aluno identificar qual é a medida do lado do piso cerâmico, ele precisa descobrir quantos pisos serão necessários para cobrir toda a sala de Ana.
E como 260:20= 13 e 300:20=15, ele pode multiplicar 13.15=195 e concluir quantos pisos cerâmicos serão necessários.
Pois, se um lado mede 260cm, serão necessários 13 pisos deste lado. Se o outro lado mede 300cm, serão necessários 15 pisos.
No desenho, o aluno pode contar quantos pisos serão necessários, ou simplesmente multiplicar a necessidade de cada dimensão, 13.15 e assim, responder a última pergunta da Ana, que serão necessários 195 pisos cerâmicos quadrados de lado 20 cm para cobrir toda a sala retangular de lados 2,6m e 3m.
Painel de soluções
Tempo sugerido: 15 minutos (Slides 5 a 10).
Orientações: Os três alunos selecionados, que usaram estratégias diferentes ao reproduzirem na lousa a resolução, devem explicar o raciocínio usado para os colegas e assiná-la.
Propósito: Incentivar que os alunos tentem explicar como calcularam o Máximo Divisor Comum dos números propostos para responderem o problema, mesmo que ainda não conheçam esse nome, de maneira intuitiva pela interpretação do problema.
Discuta com a turma:
- Qual é a diferença das estratégias usadas?
- Quais são os divisores do número 260, que representa um dos lados do retângulo (sala)?
- Quais são os divisores do número 300, que representa o outro lado do retângulo (sala)?
- Quais são os divisores dos números 260 e 300 ao mesmo tempo? Qual é o maior deles?
Na solução 1, o aluno verificou quais são os divisores de 260 e 300 ao mesmo tempo. Assim, ele descobriu quais são as possíveis medidas para o piso cerâmico. E para atender a condição da atividade, sendo o maior possível, a resposta será 20 cm.
Quando o aluno sabe os critérios de divisibilidade, agiliza a resolução da atividade. Nessa resolução, o aluno nem citou quais são os divisores, pois, a sua intenção era calcular a medida do lado do piso cerâmico que atendia a medida do lado da sala.
Na solução 2, o aluno calculou os divisores dos números 260 e 300 que representam as medidas dos lados da sala, depois verificou quais eram os divisores comuns e selecionou o maior (20cm) para atender o comando da atividade proposta.
Na solução 3, o aluno decompôs cada medida dos lados em fatores primos e assim verificou o que estava em comum, pois percebeu que existia essa necessidade de estar em comum para atender os dois lados da sala (260cm e 300cm). E assim, concluiu que 20 cm é a medida que satisfaz as condições solicitadas por Ana.
Os alunos obtiveram os divisores pelo processo geométrico, pelas divisões e fatorações sucessivas, mas essas não são as únicas resoluções.
Após o aluno identificar qual é a medida do lado do piso cerâmico, ele precisa descobrir quantos pisos serão necessários para cobrir toda a sala de Ana.
E como 260:20= 13 e 300:20=15, ele pode multiplicar 13.15=195 e concluir quantos pisos cerâmicos serão necessários.
Pois, se um lado mede 260cm, serão necessários 13 pisos deste lado. Se o outro lado mede 300cm, serão necessários 15 pisos.
No desenho, o aluno pode contar quantos pisos serão necessários, ou simplesmente multiplicar a necessidade de cada dimensão, 13.15 e assim, responder a última pergunta da Ana, que serão necessários 195 pisos cerâmicos quadrados de lado 20 cm para cobrir toda a sala retangular de lados 2,6m e 3m.
Painel de soluções
Tempo sugerido: 15 minutos (Slides 5 a 10).
Orientações: Os três alunos selecionados, que usaram estratégias diferentes ao reproduzirem na lousa a resolução, devem explicar o raciocínio usado para os colegas e assiná-la.
Propósito: Incentivar que os alunos tentem explicar como calcularam o Máximo Divisor Comum dos números propostos para responderem o problema, mesmo que ainda não conheçam esse nome, de maneira intuitiva pela interpretação do problema.
Discuta com a turma:
- Qual é a diferença das estratégias usadas?
- Quais são os divisores do número 260, que representa um dos lados do retângulo (sala)?
- Quais são os divisores do número 300, que representa o outro lado do retângulo (sala)?
- Quais são os divisores dos números 260 e 300 ao mesmo tempo? Qual é o maior deles?
Na solução 1, o aluno verificou quais são os divisores de 260 e 300 ao mesmo tempo. Assim, ele descobriu quais são as possíveis medidas para o piso cerâmico. E para atender a condição da atividade, sendo o maior possível, a resposta será 20 cm.
Quando o aluno sabe os critérios de divisibilidade, agiliza a resolução da atividade. Nessa resolução, o aluno nem citou quais são os divisores, pois, a sua intenção era calcular a medida do lado do piso cerâmico que atendia a medida do lado da sala.
Na solução 2, o aluno calculou os divisores dos números 260 e 300 que representam as medidas dos lados da sala, depois verificou quais eram os divisores comuns e selecionou o maior (20cm) para atender o comando da atividade proposta.
Na solução 3, o aluno decompôs cada medida dos lados em fatores primos e assim verificou o que estava em comum, pois percebeu que existia essa necessidade de estar em comum para atender os dois lados da sala (260cm e 300cm). E assim, concluiu que 20 cm é a medida que satisfaz as condições solicitadas por Ana.
Os alunos obtiveram os divisores pelo processo geométrico, pelas divisões e fatorações sucessivas, mas essas não são as únicas resoluções.
Após o aluno identificar qual é a medida do lado do piso cerâmico, ele precisa descobrir quantos pisos serão necessários para cobrir toda a sala de Ana.
E como 260:20= 13 e 300:20=15, ele pode multiplicar 13.15=195 e concluir quantos pisos cerâmicos serão necessários.
Pois, se um lado mede 260cm, serão necessários 13 pisos deste lado. Se o outro lado mede 300cm, serão necessários 15 pisos.
No desenho, o aluno pode contar quantos pisos serão necessários, ou simplesmente multiplicar a necessidade de cada dimensão, 13.15 e assim, responder a última pergunta da Ana, que serão necessários 195 pisos cerâmicos quadrados de lado 20 cm para cobrir toda a sala retangular de lados 2,6m e 3m.
Painel de soluções
Tempo sugerido: 15 minutos (Slides 5 a 10).
Orientações: Os três alunos selecionados, que usaram estratégias diferentes ao reproduzirem na lousa a resolução, devem explicar o raciocínio usado para os colegas e assiná-la.
Propósito: Incentivar que os alunos tentem explicar como calcularam o Máximo Divisor Comum dos números propostos para responderem o problema, mesmo que ainda não conheçam esse nome, de maneira intuitiva pela interpretação do problema.
Discuta com a turma:
- Qual é a diferença das estratégias usadas?
- Quais são os divisores do número 260, que representa um dos lados do retângulo (sala)?
- Quais são os divisores do número 300, que representa o outro lado do retângulo (sala)?
- Quais são os divisores dos números 260 e 300 ao mesmo tempo? Qual é o maior deles?
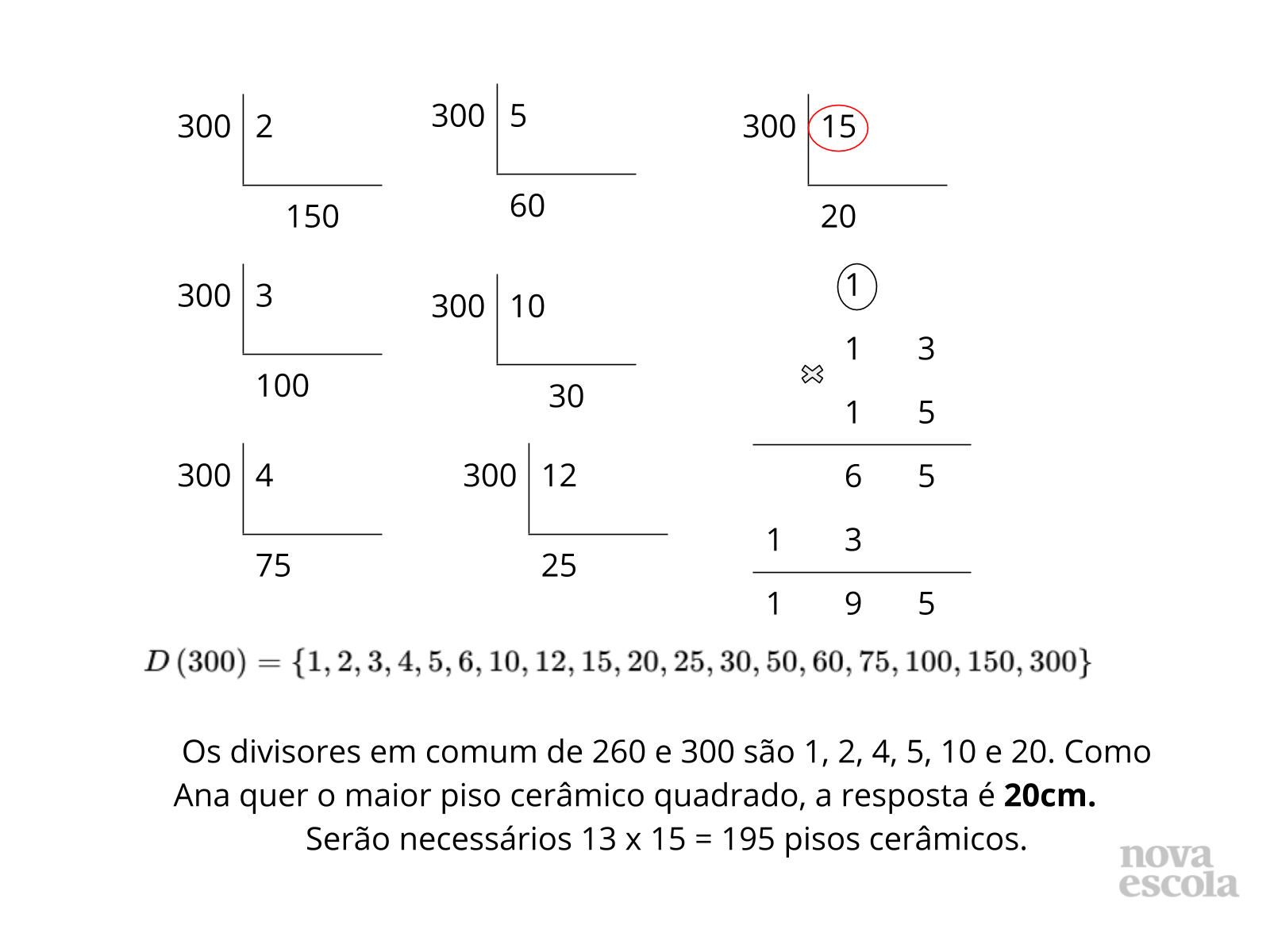
Na solução 1, o aluno verificou quais são os divisores de 260 e 300 ao mesmo tempo. Assim, ele descobriu quais são as possíveis medidas para o piso cerâmico. E para atender a condição da atividade, sendo o maior possível, a resposta será 20 cm.
Quando o aluno sabe os critérios de divisibilidade, agiliza a resolução da atividade. Nessa resolução, o aluno nem citou quais são os divisores, pois, a sua intenção era calcular a medida do lado do piso cerâmico que atendia a medida do lado da sala.
Na solução 2, o aluno calculou os divisores dos números 260 e 300 que representam as medidas dos lados da sala, depois verificou quais eram os divisores comuns e selecionou o maior (20cm) para atender o comando da atividade proposta.
Na solução 3, o aluno decompôs cada medida dos lados em fatores primos e assim verificou o que estava em comum, pois percebeu que existia essa necessidade de estar em comum para atender os dois lados da sala (260cm e 300cm). E assim, concluiu que 20 cm é a medida que satisfaz as condições solicitadas por Ana.
Os alunos obtiveram os divisores pelo processo geométrico, pelas divisões e fatorações sucessivas, mas essas não são as únicas resoluções.
Após o aluno identificar qual é a medida do lado do piso cerâmico, ele precisa descobrir quantos pisos serão necessários para cobrir toda a sala de Ana.
E como 260:20= 13 e 300:20=15, ele pode multiplicar 13.15=195 e concluir quantos pisos cerâmicos serão necessários.
Pois, se um lado mede 260cm, serão necessários 13 pisos deste lado. Se o outro lado mede 300cm, serão necessários 15 pisos.
No desenho, o aluno pode contar quantos pisos serão necessários, ou simplesmente multiplicar a necessidade de cada dimensão, 13.15 e assim, responder a última pergunta da Ana, que serão necessários 195 pisos cerâmicos quadrados de lado 20 cm para cobrir toda a sala retangular de lados 2,6m e 3m.
Painel de soluções
Tempo sugerido: 15 minutos (Slides 5 a 10).
Orientações: Os três alunos selecionados, que usaram estratégias diferentes ao reproduzirem na lousa a resolução, devem explicar o raciocínio usado para os colegas e assiná-la.
Propósito: Incentivar que os alunos tentem explicar como calcularam o Máximo Divisor Comum dos números propostos para responderem o problema, mesmo que ainda não conheçam esse nome, de maneira intuitiva pela interpretação do problema.
Discuta com a turma:
- Qual é a diferença das estratégias usadas?
- Quais são os divisores do número 260, que representa um dos lados do retângulo (sala)?
- Quais são os divisores do número 300, que representa o outro lado do retângulo (sala)?
- Quais são os divisores dos números 260 e 300 ao mesmo tempo? Qual é o maior deles?
Na solução 1, o aluno verificou quais são os divisores de 260 e 300 ao mesmo tempo. Assim, ele descobriu quais são as possíveis medidas para o piso cerâmico. E para atender a condição da atividade, sendo o maior possível, a resposta será 20 cm.
Quando o aluno sabe os critérios de divisibilidade, agiliza a resolução da atividade. Nessa resolução, o aluno nem citou quais são os divisores, pois, a sua intenção era calcular a medida do lado do piso cerâmico que atendia a medida do lado da sala.
Na solução 2, o aluno calculou os divisores dos números 260 e 300 que representam as medidas dos lados da sala, depois verificou quais eram os divisores comuns e selecionou o maior (20cm) para atender o comando da atividade proposta.
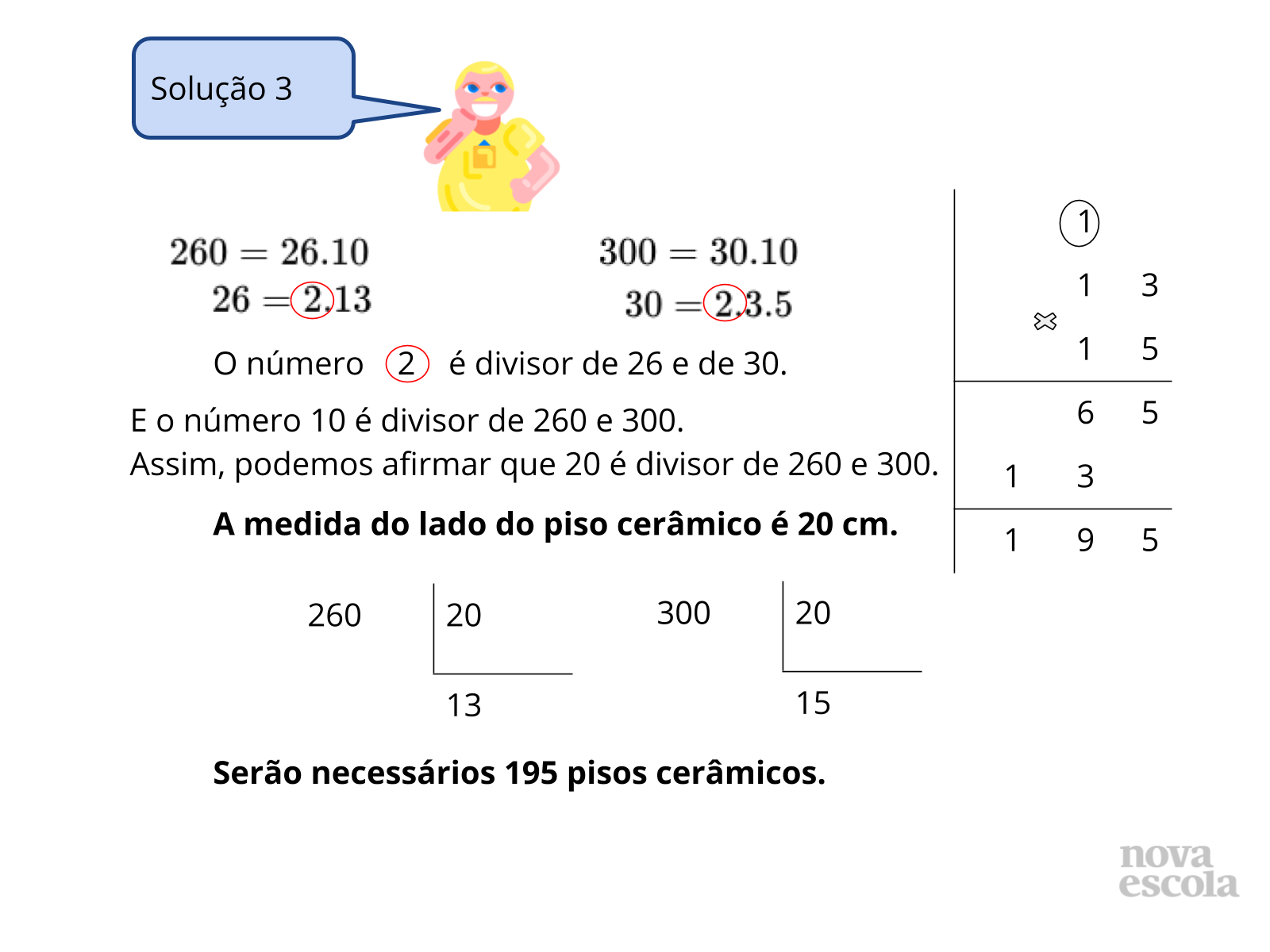
Na solução 3, o aluno decompôs cada medida dos lados em fatores primos e assim verificou o que estava em comum, pois percebeu que existia essa necessidade de estar em comum para atender os dois lados da sala (260cm e 300cm). E assim, concluiu que 20 cm é a medida que satisfaz as condições solicitadas por Ana.
Os alunos obtiveram os divisores pelo processo geométrico, pelas divisões e fatorações sucessivas, mas essas não são as únicas resoluções.
Após o aluno identificar qual é a medida do lado do piso cerâmico, ele precisa descobrir quantos pisos serão necessários para cobrir toda a sala de Ana.
E como 260:20= 13 e 300:20=15, ele pode multiplicar 13.15=195 e concluir quantos pisos cerâmicos serão necessários.
Pois, se um lado mede 260cm, serão necessários 13 pisos deste lado. Se o outro lado mede 300cm, serão necessários 15 pisos.
No desenho, o aluno pode contar quantos pisos serão necessários, ou simplesmente multiplicar a necessidade de cada dimensão, 13.15 e assim, responder a última pergunta da Ana, que serão necessários 195 pisos cerâmicos quadrados de lado 20 cm para cobrir toda a sala retangular de lados 2,6m e 3m.
Painel de soluções
Tempo sugerido: 15 minutos (Slides 5 a 10).
Orientações: Os três alunos selecionados, que usaram estratégias diferentes ao reproduzirem na lousa a resolução, devem explicar o raciocínio usado para os colegas e assiná-la.
Propósito: Incentivar que os alunos tentem explicar como calcularam o Máximo Divisor Comum dos números propostos para responderem o problema, mesmo que ainda não conheçam esse nome, de maneira intuitiva pela interpretação do problema.
Discuta com a turma:
- Qual é a diferença das estratégias usadas?
- Quais são os divisores do número 260, que representa um dos lados do retângulo (sala)?
- Quais são os divisores do número 300, que representa o outro lado do retângulo (sala)?
- Quais são os divisores dos números 260 e 300 ao mesmo tempo? Qual é o maior deles?
Na solução 1, o aluno verificou quais são os divisores de 260 e 300 ao mesmo tempo. Assim, ele descobriu quais são as possíveis medidas para o piso cerâmico. E para atender a condição da atividade, sendo o maior possível, a resposta será 20 cm.
Quando o aluno sabe os critérios de divisibilidade, agiliza a resolução da atividade. Nessa resolução, o aluno nem citou quais são os divisores, pois, a sua intenção era calcular a medida do lado do piso cerâmico que atendia a medida do lado da sala.
Na solução 2, o aluno calculou os divisores dos números 260 e 300 que representam as medidas dos lados da sala, depois verificou quais eram os divisores comuns e selecionou o maior (20cm) para atender o comando da atividade proposta.
Na solução 3, o aluno decompôs cada medida dos lados em fatores primos e assim verificou o que estava em comum, pois percebeu que existia essa necessidade de estar em comum para atender os dois lados da sala (260cm e 300cm). E assim, concluiu que 20 cm é a medida que satisfaz as condições solicitadas por Ana.
Os alunos obtiveram os divisores pelo processo geométrico, pelas divisões e fatorações sucessivas, mas essas não são as únicas resoluções.
Após o aluno identificar qual é a medida do lado do piso cerâmico, ele precisa descobrir quantos pisos serão necessários para cobrir toda a sala de Ana.
E como 260:20= 13 e 300:20=15, ele pode multiplicar 13.15=195 e concluir quantos pisos cerâmicos serão necessários.
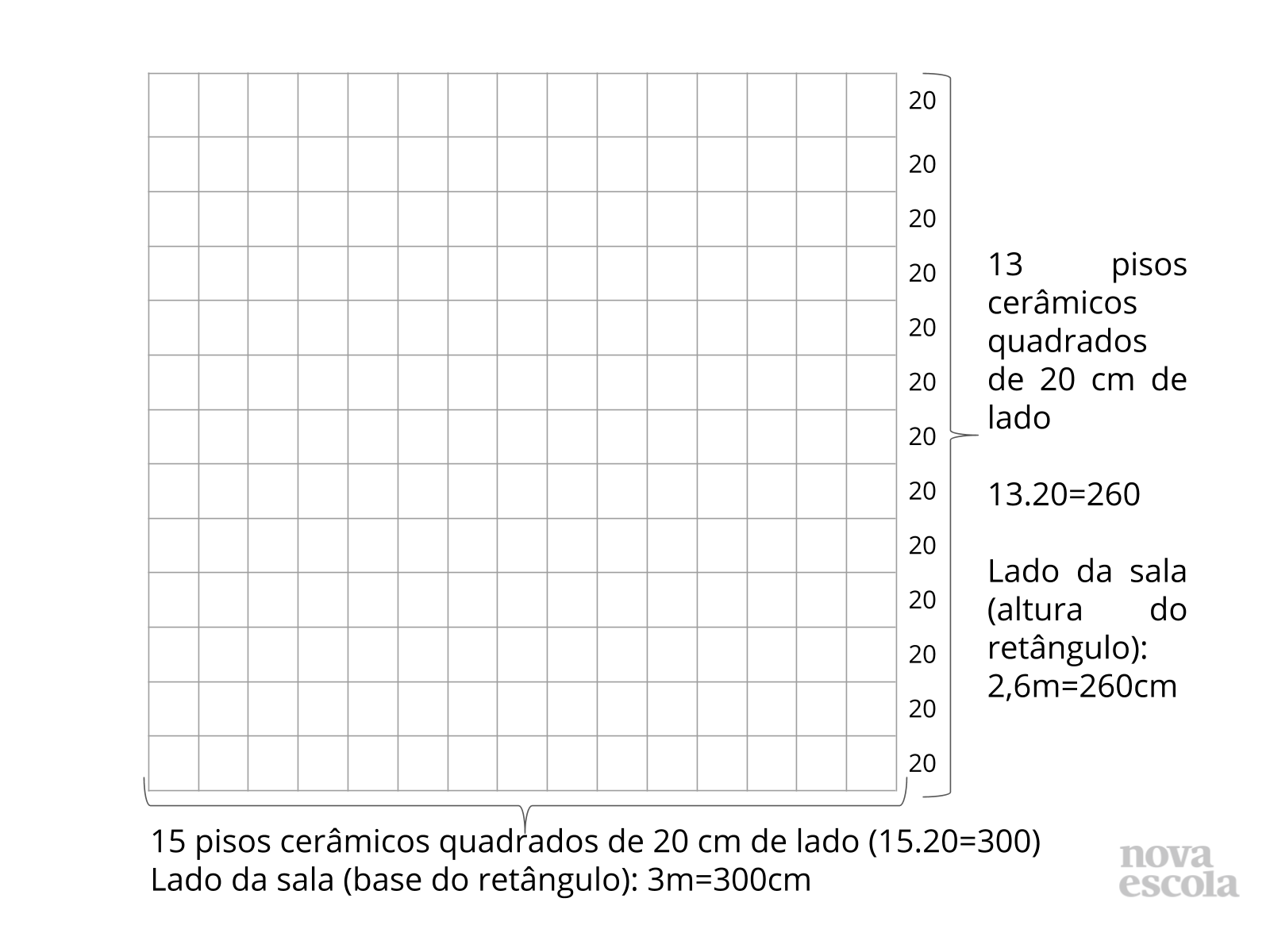
Pois, se um lado mede 260cm, serão necessários 13 pisos deste lado. Se o outro lado mede 300cm, serão necessários 15 pisos.
No desenho, o aluno pode contar quantos pisos serão necessários, ou simplesmente multiplicar a necessidade de cada dimensão, 13.15 e assim, responder a última pergunta da Ana, que serão necessários 195 pisos cerâmicos quadrados de lado 20 cm para cobrir toda a sala retangular de lados 2,6m e 3m.
Encerramento
Tempo sugerido: 5 minutos.
Orientação: Encerre a atividade retomando com os alunos o conceito de divisor, as maneiras para calculá-los e como verificar quais são os comuns para registrar o maior deles. Se desejar, anote a frase em destaque no quadro ou num cartaz para deixar exposto em sala de aula.
Enfatize com os seus alunos a necessidade de um modo prático para calcular o mdc. Pois, é relativamente simples calcular o mdc de maneira intuitiva, mas pode se tornar extremamente trabalhosa quando os números forem grandes e apresentarem grande quantidade de divisores. Sendo assim, faz-se necessário apresentarmos métodos práticos como alternativa e o aluno escolherá a estratégia que julgar conveniente em cada caso.
Material complementar:
Veja uma discussão mais detalhada sobre o MDC no final do Guia de Intervenção.
Raio x
Tempo sugerido: 8 minutos.
Orientações: Apresente o problema e peça que os alunos o resolvam individualmente. Em seguida, eles devem socializar as respostas com os outros alunos da turma. Você pode projetar, passar no quadro ou fazer cópia para os alunos. O raio x é um momento para você avaliar se todos os alunos conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um.
Propósito: O aluno precisa relembrar o que são divisores e reconhecer qual é o maior comum aos números dados.
Discuta com a turma:
- Quais são as possibilidades de formar grupos com apenas meninos?
- Como podemos formar grupos com apenas meninas?
- Qual é a condição que o professor estabeleceu?
- Para formar grupos com o mesmo número de meninos e meninas, quantos alunos poderão fazer parte dos grupos?
Materiais complementares para impressão:
