Resumo da aula
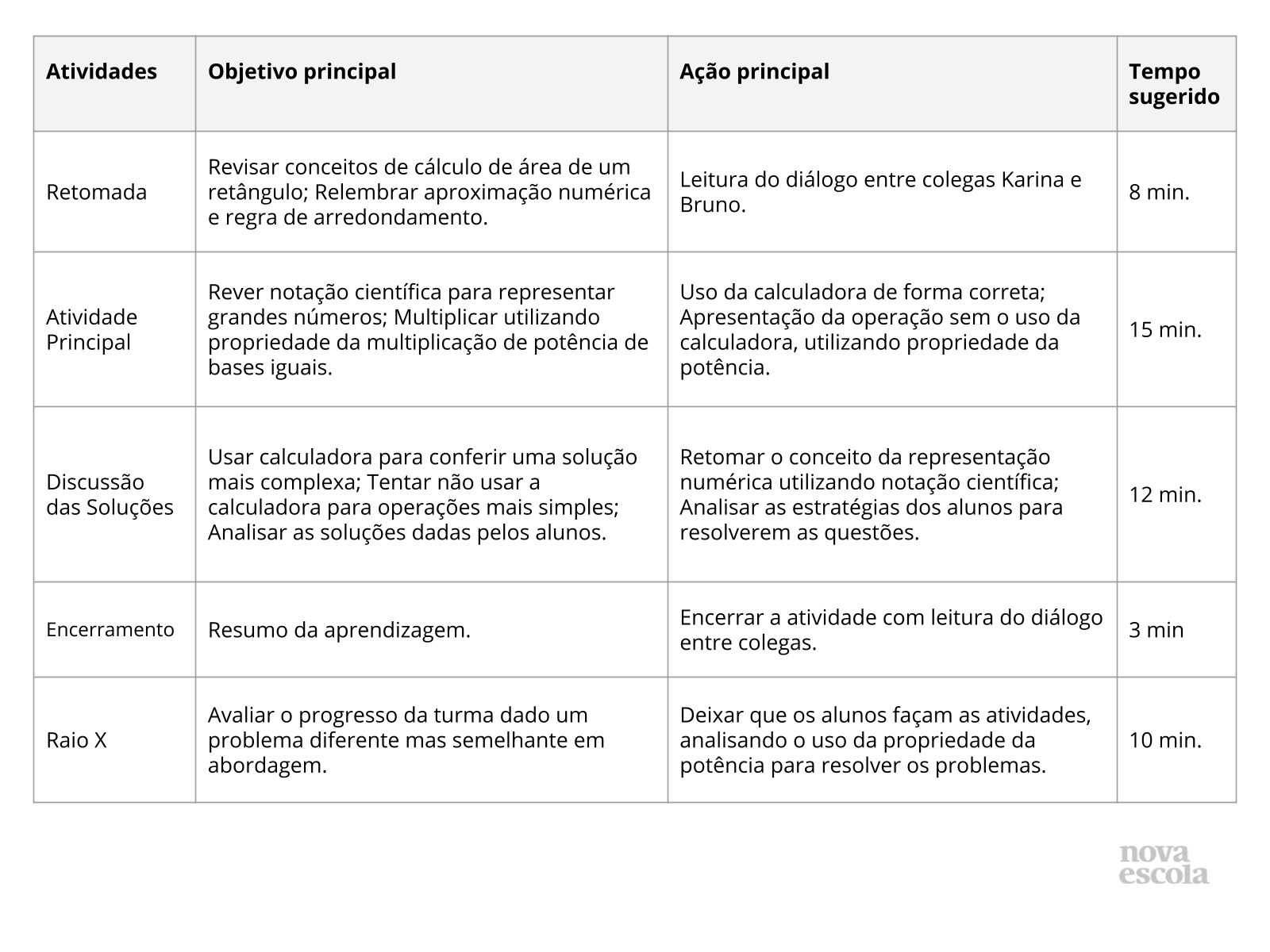
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Está aula é uma continuação e ampliação da aula anterior.
Retomada

Tempo sugerido: 8 minutos (slides 3, 4 e 5).
Orientações: Levar impresso, caso não possa ser projetado. Faça a leitura com os alunos. Pedir para um aluno fazer o papel do Bruno e uma aluna fazer o papel da Karina.
Propósito: Trazer alguns assuntos que serão abordados nesta aula na forma de uma história.
Retomada

Tempo sugerido: 8 minutos (slides 3, 4 e 5).
Orientações: Deixar os alunos terminarem a leitura.
Propósito: Relembrar a regra de arredondamento e aproximação numérica.
Discuta com a turma:
- Falar alguns números e pedir que arredondem mentalmente, dizendo em voz alta os valores aproximados.
Material complementar:
Regras de arredondamento - https://pt.wikipedia.org/wiki/Arredondamento
Retomada

Tempo sugerido: 8 minutos (slides 3, 4 e 5).
Orientações: Deixar os alunos lendo em voz baixa como uma forma de despertar a curiosidade individual.
Propósito: A ideia não é detalhar o processo de captação da imagem, mas simplesmente apresentar o sensor como uma forma plana retangular, que possui base e altura. Isso será necessário para o cálculo da área.
Material complementar:
Como funciona o sensor da câmera do seu smartphone: https://www.tecmundo.com.br/celular/104419-como-funciona-sensor-camera-digital-smartphone-celular.htm
Atividade principal Parte I

Tempo sugerido: 15 minutos (slides 6 e 7).
Orientações:
- Peça que, em dupla ou trio, os alunos leiam a atividade e a realizem usando a calculadora. Caso eles tenham calculadora científica, é uma boa ocasião para mostrar como se usa o botão 10x. A ideia de se fazer em grupo é que um pode emprestar material para outro. Uma ideia também, se possível, é usar a calculadora do celular no modo calculadora científica.
- Ao fazer a representação de 12MP em notação científica, estimule-os a usarem propriedade da potência de mesma base 12x106=1,2x101x106=1,2x107 . Ao representar todos os números em notação científica, fica mais simples observar a ordem de grandeza e ter uma noção que são números próximos.
Propósito: Ampliar a ideia da representação de grandes números utilizando notação científica.
Discuta com a turma:
- Apesar de ambos serem considerados de 12MP, eles possuem 12MP de verdade? Não possuem, como se pode ver nos cálculos.
- Qual sensor tem melhor resolução? O sensor A tem maior resolução.
- Qual deles deve custar mais caro e por quê? Sensor A deve custar mais, se for considerado o que tem melhor resolução.
- Qual deles deve ter mais qualidade de imagem? Quanto mais pixels, melhor a qualidade. Portanto, o sensor A.
- Consegue imaginar a forma deste sensor, quadrado, retangular ou redondo? Retangular
Materiais complementares para impressão:
Atividade principal
Resolução da atividade principal
Agrupamento Produtivo - Trabalho em Grupo: https://novaescola.org.br/guias/1152/agrupamento-produtivo/1378/trabalho-em-grupo
Agrupamento Produtivo - Trabalho em Dupla: https://novaescola.org.br/guias/1152/agrupamento-produtivo/1379/trabalho-em-dupla
Como agrupo meus alunos? https://novaescola.org.br/conteudo/1475/como-agrupo-meus-alunos
As trocas que fazem a turma avançar: https://novaescola.org.br/conteudo/366/as-trocas-que-fazem-a-turma-avancar
Atividade principal Parte II

Tempo sugerido: 15 minutos (slides 6 e 7).
Orientações: Peça que, em dupla ou trio, os alunos leiam a atividade e a realizem sem a calculadora. Uns podem ajudar os outros com a propriedade da potência, multiplicação com bases iguais somam-se os expoentes.
Propósito: Mostrar o quanto se torna fácil fazer uma operação com grandes números representados na forma de potência. Basicamente, é um exercício semelhante ao anterior, mas aqui os alunos podem antever os resultados, fazendo contas de cabeça e conferindo as contas no papel. E depois representar em notação científica faz com que eles tenham uma noção maior da ordem de grandeza.
Discuta com a turma:
Interessante neste momento conversar com a turma sobre o não uso da calculadora. “O que vocês acham turma? Multiplicamos 5500 x 2900 ou 5,5 x 2,9 e utilizar propriedade da multiplicação de potência de mesma base? Lembrem-se, vamos nos esforçar um pouco para fazer sem o uso de calculadora.”
Painel de soluções

Tempo sugerido: 12 minutos (slides 8 e 9).
Orientações:
- Fique atento às soluções dos alunos. Se houver muitas dificuldades na escrita em notação científica, volte ao plano conceitual e trabalhe atividades complementares.
- Ao arredondar números, os valores aproximados podem sair diferente e dependendo da precisão das operações. Deve-se pensar melhor a respeito de quantas casas decimais são aceitas. Para este caso, como os sensores são considerados de 12 megapixels, é até aceitável o arredondamento prévio para simplificar a operação sem o uso de calculadora.
- Lembrar alguns fatores multiplicadores tais como k = 103, M = 106 e G = 109.
Propósito: Incentivar que os alunos tentem explicar o raciocínio utilizado para solucionar uma questão. Espera-se que os estudantes sejam capazes de refletir sobre suas estratégias.
Discuta com a turma:
- O uso da calculadora neste caso ajudou ou atrapalhou? (Enfatize que com algumas mudanças a operação se torna mais simples de se fazer mesmo sem a calculadora.)
- Quando arredondar antes de efetuar a operação e quando arredondar depois?
Painel de soluções

Tempo sugerido: 12 minutos (slides 8 e 9).
Orientações:
- Fique atento às soluções dos alunos. Se houver muitas dificuldades na escrita em notação científica, volte ao plano conceitual e trabalhe atividades complementares.
- Ao arredondar números, os valores aproximados podem sair diferente e dependendo da precisão das operações. Deve-se pensar melhor a respeito de quantas casas decimais são aceitas. Para este caso, como os sensores são considerados de 12 megapixels, é até aceitável o arredondamento prévio para simplificar a operação sem o uso de calculadora.
- Lembrar alguns fatores multiplicadores tais como k = 103, M = 106 e G = 109.
Propósito: Incentivar que os alunos tentem explicar o raciocínio utilizado para solucionar uma questão. Espera-se que os estudantes sejam capazes de refletir sobre suas estratégias.
Discuta com a turma:
- O uso da calculadora neste caso ajudou ou atrapalhou? (Enfatize que com algumas mudanças a operação se torna mais simples de se fazer mesmo sem a calculadora.)
- Quando arredondar antes de efetuar a operação e quando arredondar depois?
Encerramento

Tempo sugerido: 3 minutos.
Orientação: Encerre a atividade apresentando a notação científica como solução de representação numérica para números grandes, além de poder unir conhecimentos anteriores tais como aproximação numérica e propriedades da potência.
Raio x

Tempo sugerido: 10 minutos.
Orientações: Peça que, individualmente, os alunos leiam a atividade e a realizem. Circule para verificar como os alunos estão realizando a representação dos números. O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. Deixe-os resolver como bem entenderem, usando calculadora ou não. No final, reserve um tempo para um debate coletivo registrando as soluções no quadro.
Propósitos: Verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante e avaliar os conhecimentos de cada um a respeito da representação de números grandes utilizando a notação científica. Entender qual o método escolhido para realizar as operações.
Materiais complementares para impressão:
Raio X
Resolução do Raio X
Atividade complementar
Resolução da atividade complementar
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. 




















