Aquecimento
Plano de Aula
Plano de aula: Reformando a piscina
Plano 3 de uma sequência de 10 planos. Veja todos os planos sobre Resolução de problemas de medidas envolvendo grandezas
Descrição
Reformando a piscina.
Autor: Dariel Barbosa de Melo Jr
Mentor: Maria Aparecida Nemet
Especialista de área: Fernando Barnabé
Habilidade da BNCC
(EF06MA22) Reconhecer que o resultado de uma medida depende da unidade de medida utilizada.
Objetivos específicos
- Relacionar as medidas de capacidade (ml, litro) e volume (cm³, dm³, m³)
- Resolver problemas de volume que envolvam as transformações de unidades.
Conceito-chave
Medidas volume e capacidade.
Recursos necessários
- Copo medidor de laboratório, de cozinha, ou mesmo feito pelo professor, utilizando garrafa pet.
- Calculadora (caso o professor julgue necessário)
- Atividades impressas em folhas, coladas no caderno ou não.
Habilidades BNCC:
Objetivos de aprendizagem
- Relacionar as medidas de capacidade (ml, litro) e volume (cm³, dm³, m³)
- Resolver problemas de volume que envolvam as transformações de unidades.
Resumo da aula
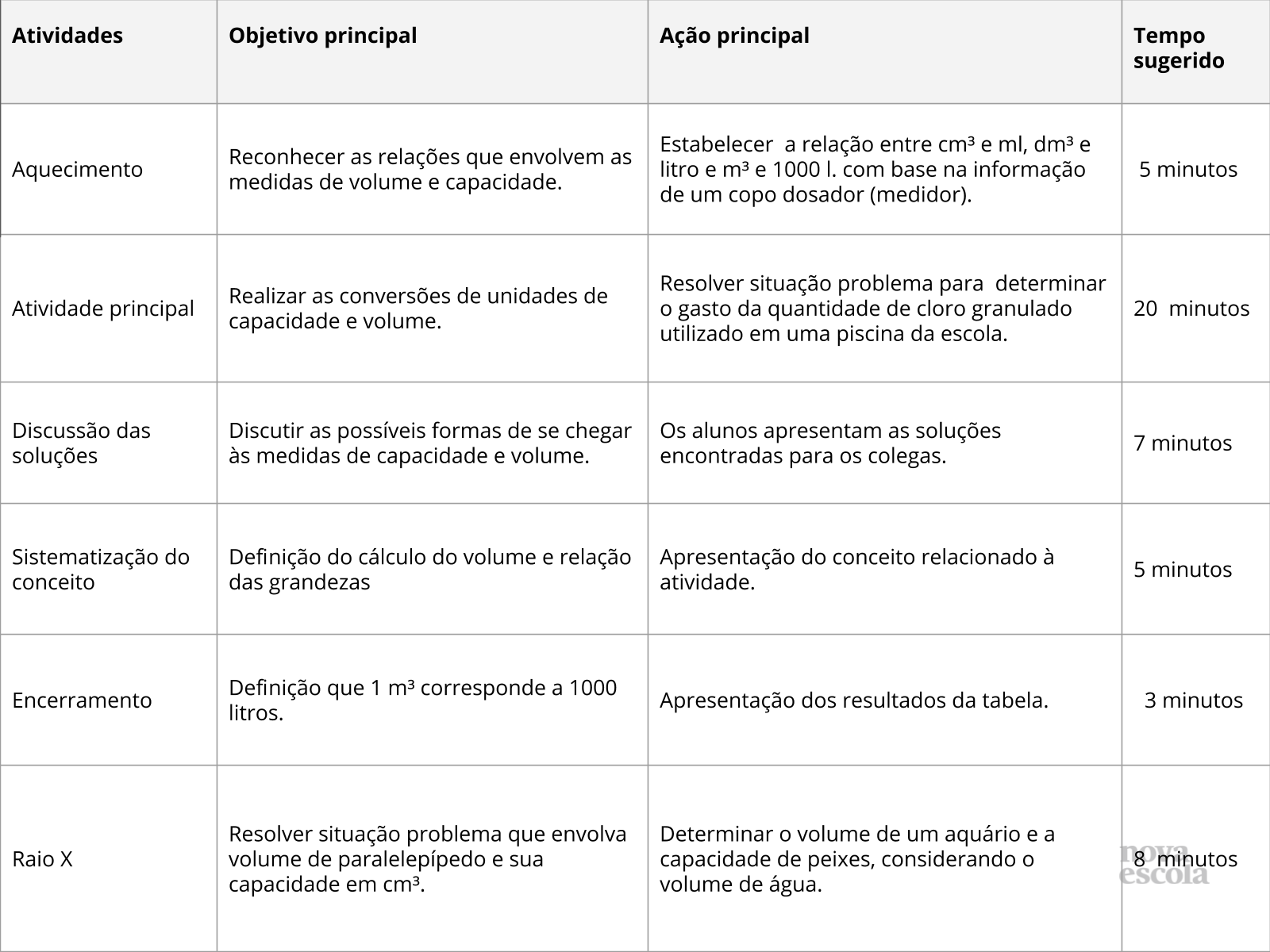 Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Aquecimento

Tempo sugerido: 5 minutos (slides 3 e 4)
Orientação: Entregue a cada grupo um copo dosador (medidor), esse copo pode ser um Béquer do laboratório de química da escola, ou um medidor de cozinha, ou ainda um copo produzido com a base de garrafa pet.
No copo de medidas, o professor deve acrescentar do lado da medida 500 ml, o valor 500 cm³.
Os alunos devem preencher a tabela de relação de grandezas.
Propósito:Reconhecer a relação entre 1000 cm³ e 1 litro.
Aquecimento

Tempo sugerido: 5 minutos (slides 3 e 4)
Orientação: Observando as informações da tabela, espera-se que os alunos relacionem 1000cm³ a 1 litro, consequentemente, que 1000 litros correspondem a 1.000.000 cm³ , que é o produto de 100cm x 100cm x 100cm, ou 1m x 1m x 1m, e finalmente, que 1 m³ corresponde a 1000 litros.
Essa relação completa a tabela de Relação de grandezas.
Propósito:Reconhecer a relação entre 1 m³ e 1000 litros.
Materiais complementares para impressão:
Atividade Principal

Tempo sugerido: 20 minutos (slides 5 a 7)
Orientação:
Para a realização dessa atividade os alunos deverão realizar algumas conversões de grandezas.
De início, determinar o volume da piscina, o que pode ser feito através do produto das grandezas comprimento, largura e altura da água, utilizando m³ ou convertendo m em cm e determinar o volume em cm³.
É importante que o professor observe se essas relações estão corretas. Um caminho interessante é a conversão das unidades de comprimento em metros por centímetros, já que a informação do exercício é que 500cm³ equivalem a 500ml.
Permita que os alunos utilizem calculadoras, para que o foco do exercício não recaia nos cálculos. O professor pode auxiliar a turma nas operações que os alunos apresentem dificuldade.
Discuta com a Turma: Como a relação 500cm³ para 500ml pode ser utilizada em m³ e litros?
Propósito: Utilizar as relações entre grandezas de capacidade e volume.
Atividade Principal <title/>

Atividade Principal
Tempo sugerido: 20 minutos (slides 5 a 7)
Orientação: Auxiliar os alunos na relação 1000cm³ = 1000ml = 1 litro, assim o cálculo do volume utilizando cm passa a ter significado. 1000000 cm³ = 1000 litros ou 1m³ = 1000 litros.
Reflexão: Como a relação 500cm³ para 500ml pode ser utilizada em m³ e litros?
Propósito: Utilizar as relações entre grandezas de capacidade e volume.
Atividade Principal

Tempo sugerido: 20 minutos (slides 5 a 7)
Orientação: Auxiliar os alunos na relação 1000cm³ = 1000ml = 1 litro, assim o cálculo do volume utilizando cm passa a ter significado. 1.000.000 cm³ = 1000 litros ou 1m³ = 1000 litros.
Discuta com a turma: Como a relação 500cm³ para 500ml pode ser utilizada em m³ e litros?
Propósito: Utilizar as relações entre grandezas de capacidade e volume.
Materiais complementares para impressão:
Discussão das soluções

Tempo sugerido: 7 minutos (slides 8 a 10)
Orientação: Proponha aos alunos a apresentar suas tabelas e os resultados encontrados.
Discuta com a turma:
Sabemos que cm³ se relaciona diretamente com ml, e as outras grandezas? Qual é a relação de dm³ e litro e m³ e litros?
Propósito: Reconhecer as relações entre capacidade e volume, com destaque, 1 m³ representam 1000 litros.
Discussão das soluções

Tempo sugerido: 7 minutos (slides 8 a 10)
Orientação: Proponha aos alunos a apresentar suas tabelas e os resultados encontrados.
Discuta com a turma:
Sabemos que cm³ se relaciona diretamente com ml, e as outras grandezas? Qual é a relação de dm³ e litro e m³ e litros?
Propósito: Reconhecer as relações entre capacidade e volume, com destaque, 1 m³ representam 1000 litros.
Discussão das soluções

Tempo sugerido: 7 minutos (slides 8 a 10)
Orientação: Proponha aos alunos a apresentar suas tabelas e os resultados encontrados.
Discuta com a turma:
Sabemos que cm³ se relaciona diretamente com ml, e as outras grandezas? Qual é a relação de dm³ e litro e m³ e litros?
Propósito: Reconhecer as relações entre capacidade e volume, com destaque, 1 m³ representam 1000 litros.
Sistematização do conceito

Tempo sugerido: 5 minutos.
Orientação: Apresentação dos resultados da tabela, destacando as relações entre as grandezas.
Propósito: Definição que 1 m³ corresponde a 1000 litros.
Encerramento
Tempo sugerido: 3 minutos.
Orientação: Com os resultados obtidos na atividade principal, os alunos devem relacionar as unidades de volume e capacidade.
Propósito: Reconhecer as relações entre capacidade e volume, com destaque, 1 m³ representam 1000 litros.
Raio x

Tempo sugerido: 8 minutos (slides 13 e 14)
Orientação: Auxiliar os alunos na relação 1000cm³ = 1000ml = 1 litro, assim o cálculo do volume utilizando cm passa a ter significado. 1000000 cm³ = 1000 litros ou 1m³ = 1000 litros.
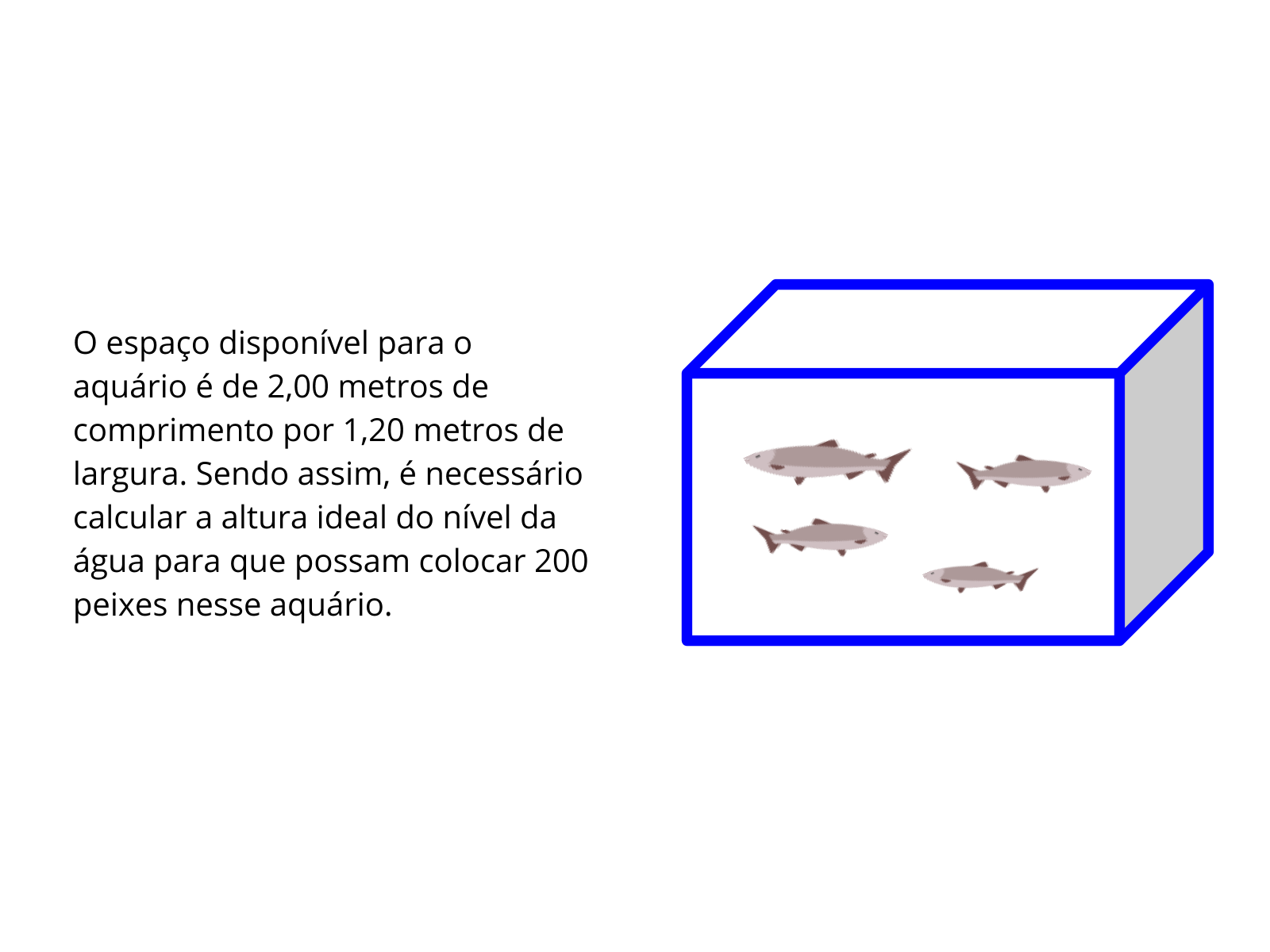
Discuta com a turma: Como a proposta da escola é ter 200 peixes de 6 cm cada, portanto 6 litros de água por peixe, temos:
200 peixes x 6 litros = 1 200 litros
Como a relação 500cm³ para 500ml pode ser utilizada em m³ e litros?
Relações :
a)1 m³ equivale a 1000 litros de água, portanto o aquário necessita ter 1,2 m³ de volume.
b)1 dm equivale a 10 cm, 1 dm³ equivale a 1 litro de água, 1 dm equivale a 10 cm, Portanto 1 dm³ equivale a 10cm x 10cm x 10cm ou 1000 cm³. Sendo assim 1000 cm³ equivale a 1 litro.
Multiplicando 1 200 litros por 1000, teremos 1200000 cm³
Propósito: Utilizar as relações entre grandezas de capacidade e volume.
Raio x
Tempo sugerido: 8 minutos (slides 13 e 14)
Orientação: Auxiliar os alunos na relação 1000cm³ = 1000ml = 1 litro, assim o cálculo do volume utilizando cm passa a ter significado. 1000000 cm³ = 1000 litros ou 1m³ = 1000 litros.
Discuta com a turma: Como a proposta da escola é ter 200 peixes de 6 cm cada, portanto 6 litros de água por peixe, temos:
200 peixes x 6 litros = 1 200 litros
Como a relação 500cm³ para 500ml pode ser utilizada em m³ e litros?
Relações :
a)1 m³ equivale a 1000 litros de água, portanto o aquário necessita ter 1,2 m³ de volume.
b)1 dm equivale a 10 cm, 1 dm³ equivale a 1 litro de água, 1 dm equivale a 10 cm, Portanto 1 dm³ equivale a 10cm x 10cm x 10cm ou 1000 cm³. Sendo assim 1000 cm³ equivale a 1 litro.
Multiplicando 1 200 litros por 1000, teremos 1200000 cm³
Propósito: Utilizar as relações entre grandezas de capacidade e volume.
Materiais complementares para impressão:
Resolução da Atividade complementar
Sugestão de adaptaçãoSugestão de adaptaçãopara ensino remoto
Código do plano
MAT6_19GRMO03
Recursos
- Necessários: Folha sulfite, lápis, caderno
- Opcionais: Meet, Zoom, WhatsApp, Google sala de Aula
Introdução ao volume: https://pt.khanacademy.org/math/basic-geo/basic-geo-volume-sa/volume-rect-prism/v/how-we-measure-volume
Volume de um prisma retangular: https://pt.khanacademy.org/math/basic-geo/basic-geo-volume-sa/volume-rect-prism/v/volume-of-a-rectangular-prism-or-box-examples
Para este plano, foque na etapa: Atividade Principal
Aquecimento
Você pode fazer uma sala de aula invertida. Envie com antecedência o link do vídeo e o roteiro de perguntas para seus alunos (WhatsApp), sugerindo a visualização do vídeo “Sistema métrico: unidades de medidas” disponível no Khan Academy. Após a visualização do vídeo peça que respondam às questões e registrem no seu caderno de estudo. Qual a relação de 1litro com a caixa de 10cm? Qual a relação do litro com mL? E a relação do mL com cm? Você saberia responder se 1000cm³ equivale a 1L?
Atividade Principal (adaptada)
Professor, para a realização da atividade principal os alunos precisam ter acesso ao problema proposto. Compartilhe os slides de 5 a 7. Você pode tirar uma foto e disponibilizar a imagem no grupo de whatsapp ou no Google Sala de Aula para que os alunos possam pensar sobre ela. Oriente-os a fotografar as suas estratégias e respostas para compartilhar com o professor e a turma no momento da discussão das soluções. Sugerimos que envie um áudio e/ou vídeo orientativo. Mantenha um canal de comunicação para dúvidas e esclarecimentos antes do encontro combinado. No dia do encontro marcado (Meet, Hangouts, Zoom, Teams), deixe que os alunos compartilhem seus desenhos. Se sua aula fora assíncrona, deixe a tarefa na escola ou envie pelo WhatsApp. Grave um áudio explicando e peçam que enviem para você combinando um retorno de devolutiva. Nesse retorno, você pode enviar o print com registros dos outros alunos para que eles comparem com suas estratégias e colem no seu caderno como repertório de soluções.
Discussão das soluções
Professor, esse é um dos momentos mais importantes da aula, portanto fique atento às respostas dos alunos. Solicite aos alunos que apresentem suas soluções sobre cada um dos itens. Pergunte: cm³ se relaciona diretamente com ml? e as outras grandezas? Qual é a relação de dm³ e litro e m³ e litros? Use a Sistematização e o encerramento para fazer o “fechamento” da sua aula. Caso sua aula seja síncrona, você pode explorar esse momento solicitando aos alunos que acionem os microfones e expliquem como chegaram às soluções. Caso contrário, peça que enviem as explicações por mensagens de áudio pelo WhatsApp. Outra possibilidade é os alunos fotografarem seus registros para compartilhar no grupo de WhatsApp.
Raio X
Use o Raio X e as atividades complementares como forma de revisão para consolidação das aprendizagens. Não esqueça de retomar discussões também dessas atividades e focar nos pontos de aprendizagem mais críticos.
Convite às famílias
A participação das famílias no processo de aprendizagem é de grande importância para o aluno. Porém, ressaltamos que os pais não são professores de matemática e muitos estão ocupados com outras funções em casa. Portanto, indicamos a participação das famílias no compartilhamento e discussão de possíveis soluções para os problemas propostos.
Reformando a piscina.
Autor: Dariel Barbosa de Melo Jr
Mentor: Maria Aparecida Nemet
Especialista de área: Fernando Barnabé
Habilidade da BNCC
(EF06MA22) Reconhecer que o resultado de uma medida depende da unidade de medida utilizada.
Objetivos específicos
- Relacionar as medidas de capacidade (ml, litro) e volume (cm³, dm³, m³)
- Resolver problemas de volume que envolvam as transformações de unidades.
Conceito-chave
Medidas volume e capacidade.
Recursos necessários
- Copo medidor de laboratório, de cozinha, ou mesmo feito pelo professor, utilizando garrafa pet.
- Calculadora (caso o professor julgue necessário)
- Atividades impressas em folhas, coladas no caderno ou não.