Aquecimento
Plano de Aula
Plano de aula: A Maquete e os paralelepípedos
Plano 4 de uma sequência de 10 planos. Veja todos os planos sobre Resolução de problemas de medidas envolvendo grandezas
Descrição
Habilidade da BNCC
(EF06MA22) Reconhecer que o resultado de uma medida depende da unidade de medida utilizada.
Objetivos específicos
- Relacionar as medidas de capacidade (litro) e volume (dm³)
- Traçar estratégias para construção de paralelepípedos.
Conceito-chave
Medidas de volume e capacidade.
Recursos necessários
- Calculadora (caso o professor julgue necessário)
- Atividades impressas em folhas, para colar no caderno.
Habilidades BNCC:
Objetivos de aprendizagem
- Relacionar as medidas de capacidade (litro) e volume (dm³)
- Traçar estratégias para construção de paralelepípedos.
Resumo da aula
Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivos

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Aquecimento
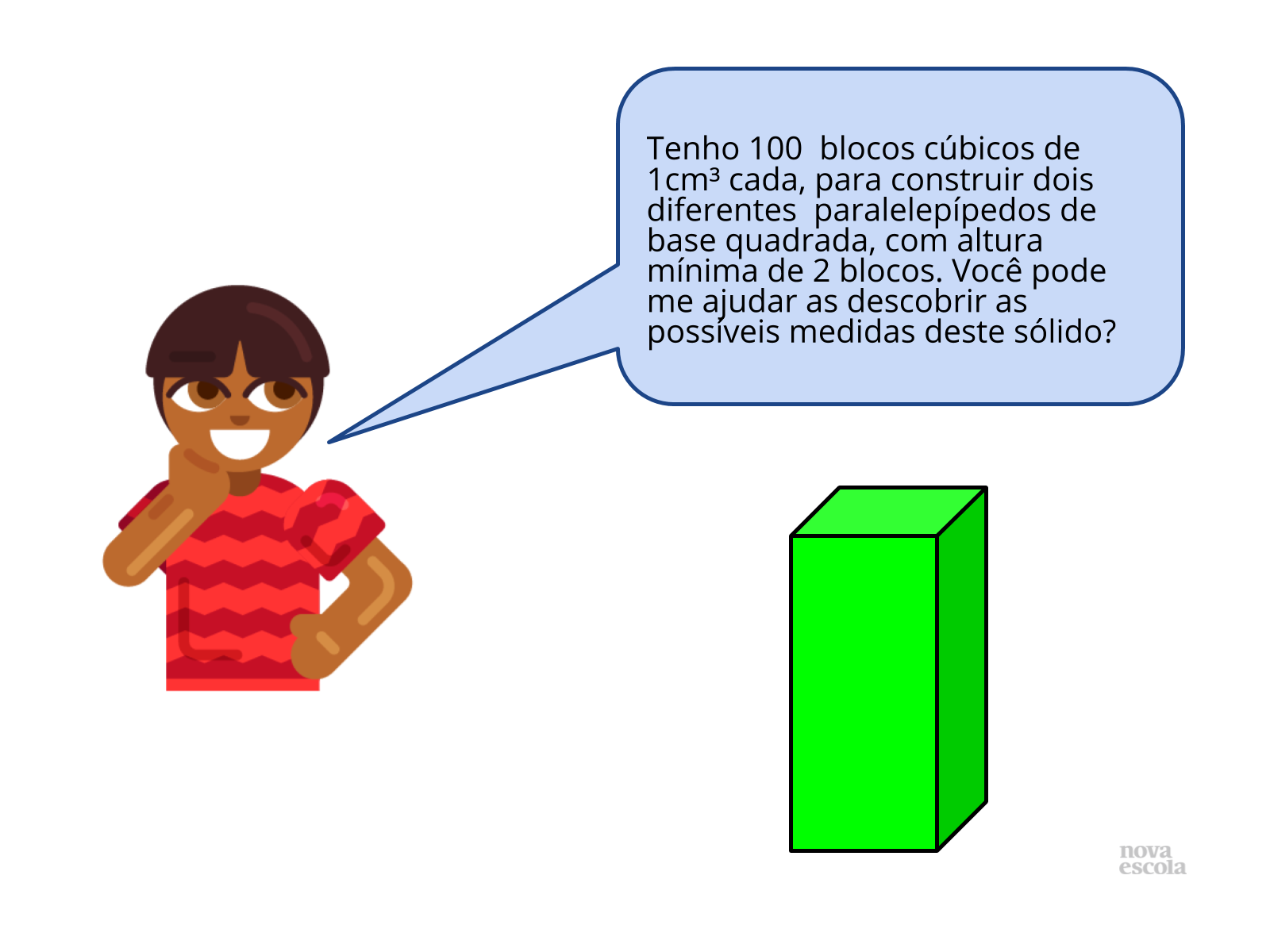
Tempo sugerido: 5 minutos.
Orientação: Nessa atividade, os alunos deverão planejar a construção de dois paralelepípedos, com base quadrada, com o total de 100 blocos de 1cm³.
Propósito: Desenvolver a prática de planejamento em uma atividade de volume, com várias possíveis soluções.
Discuta: Quais as possíveis soluções para a atividade? Soluções diferentes são erradas?
Atividade Principal
Tempo sugerido: 25 minutos.
Orientação:
- Apresentação da atividade.
Propósito: Apresentar a atividade aos alunos.
Materiais complementares para impressão
Resolução da atividade principal
Atividade Principal
Tempo sugerido: 25 minutos.
Orientação:
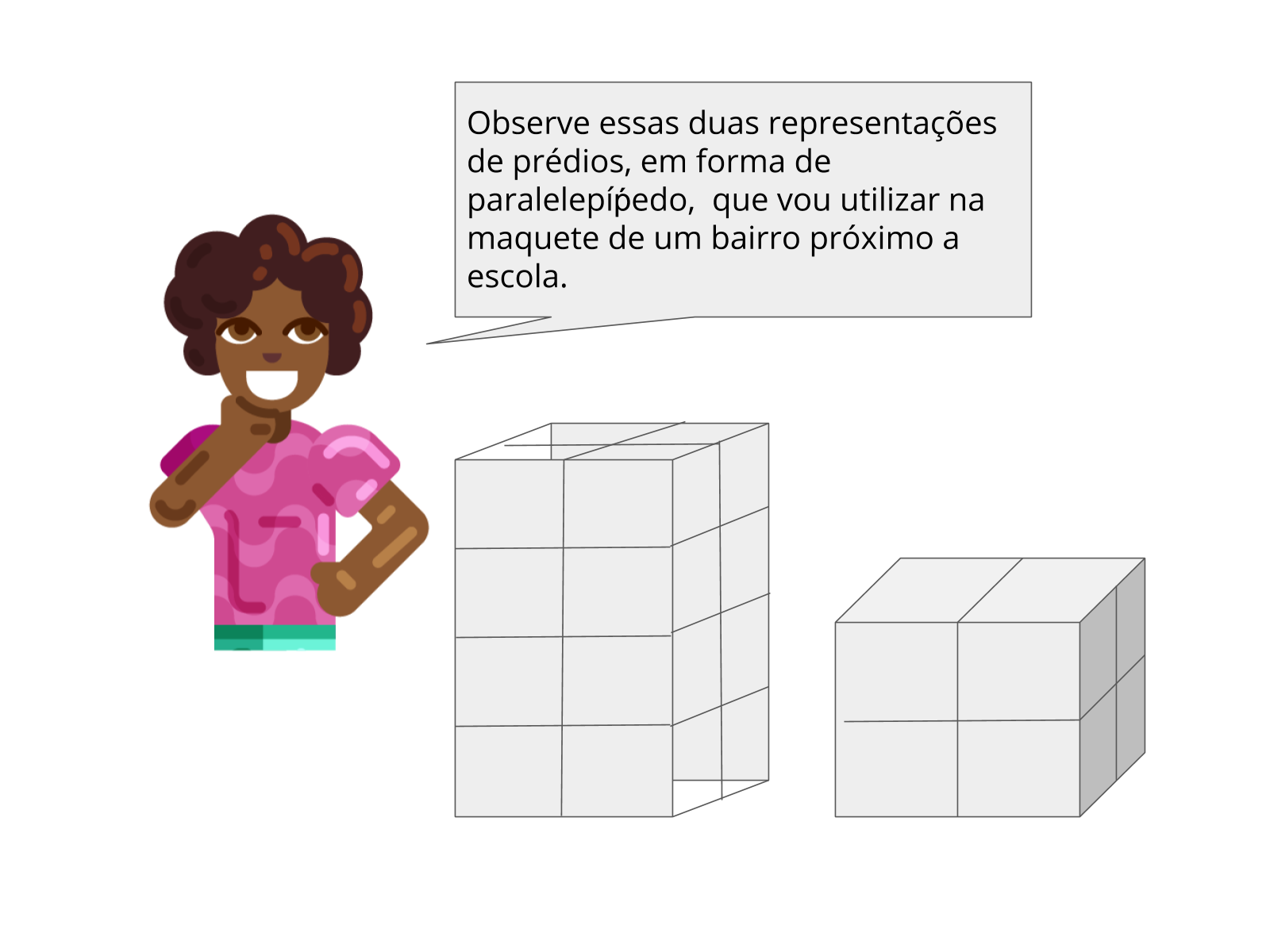
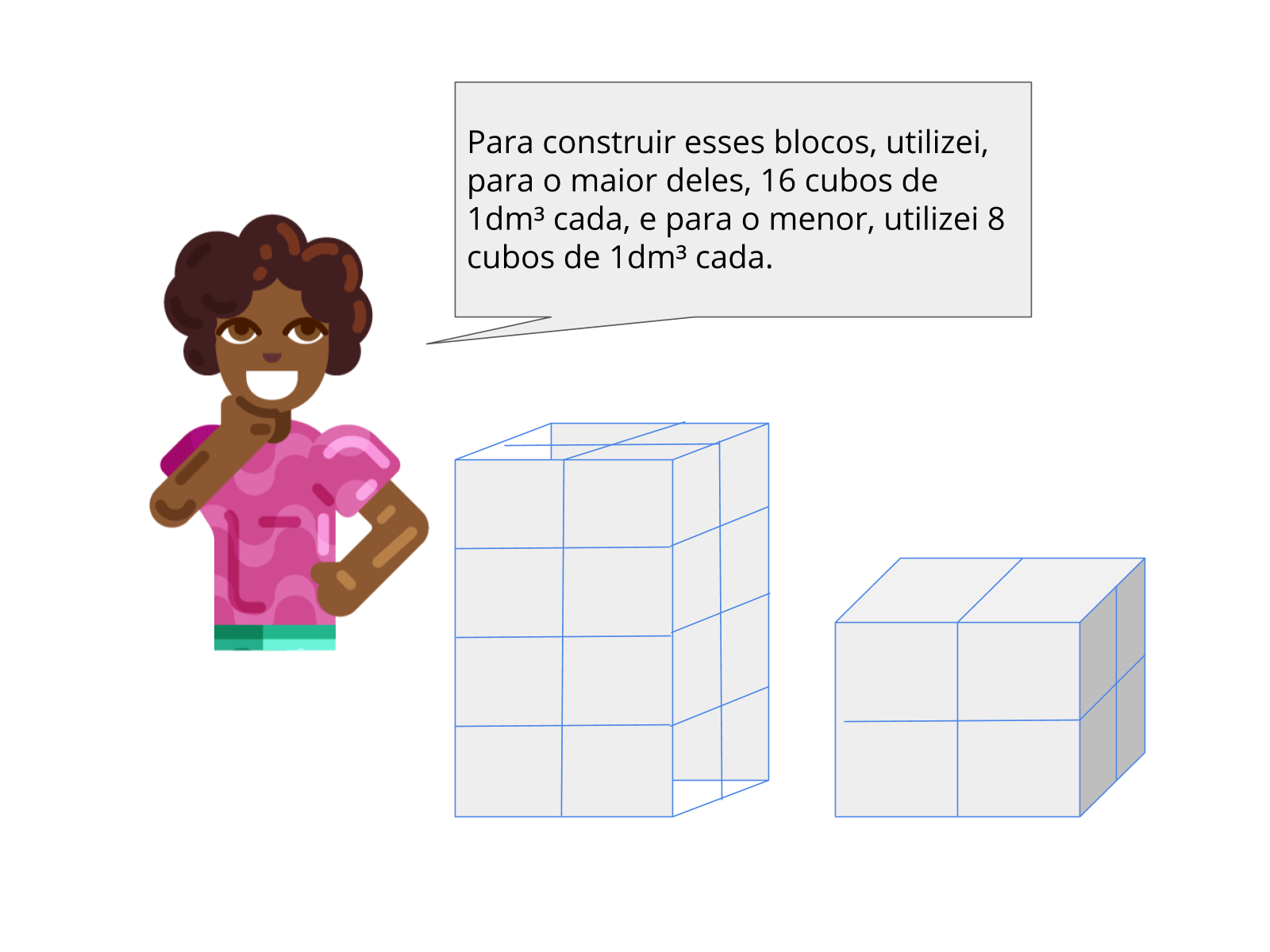
O primeiro slide da atividade é um exemplo da montagem dos prédios utilizando cubos.
Para resolver a situação, os alunos devem planejar a quantidade de prédios que serão utilizados, com suas respectivas dimensões, observando as regras do professor:
- 6 prédios;
- 2 deles cúbicos;
- 2 com no mínimo 4 blocos de altura.
Discuta com a Turma:
- Quais as medidas dos paralelepípedos apresentados no exemplo?
Propósito:
- Preparar os alunos para os cálculos da atividade principal.
Atividade Principal

Tempo sugerido: 25 minutos.
Orientação:
Para resolver a situação, os alunos devem planejar a quantidade de prédios que serão utilizados, com suas respectivas dimensões, observando as regras do professor:
- 6 prédios;
- 2 deles cúbicos;
- 2 com no mínimo 4 blocos de altura.
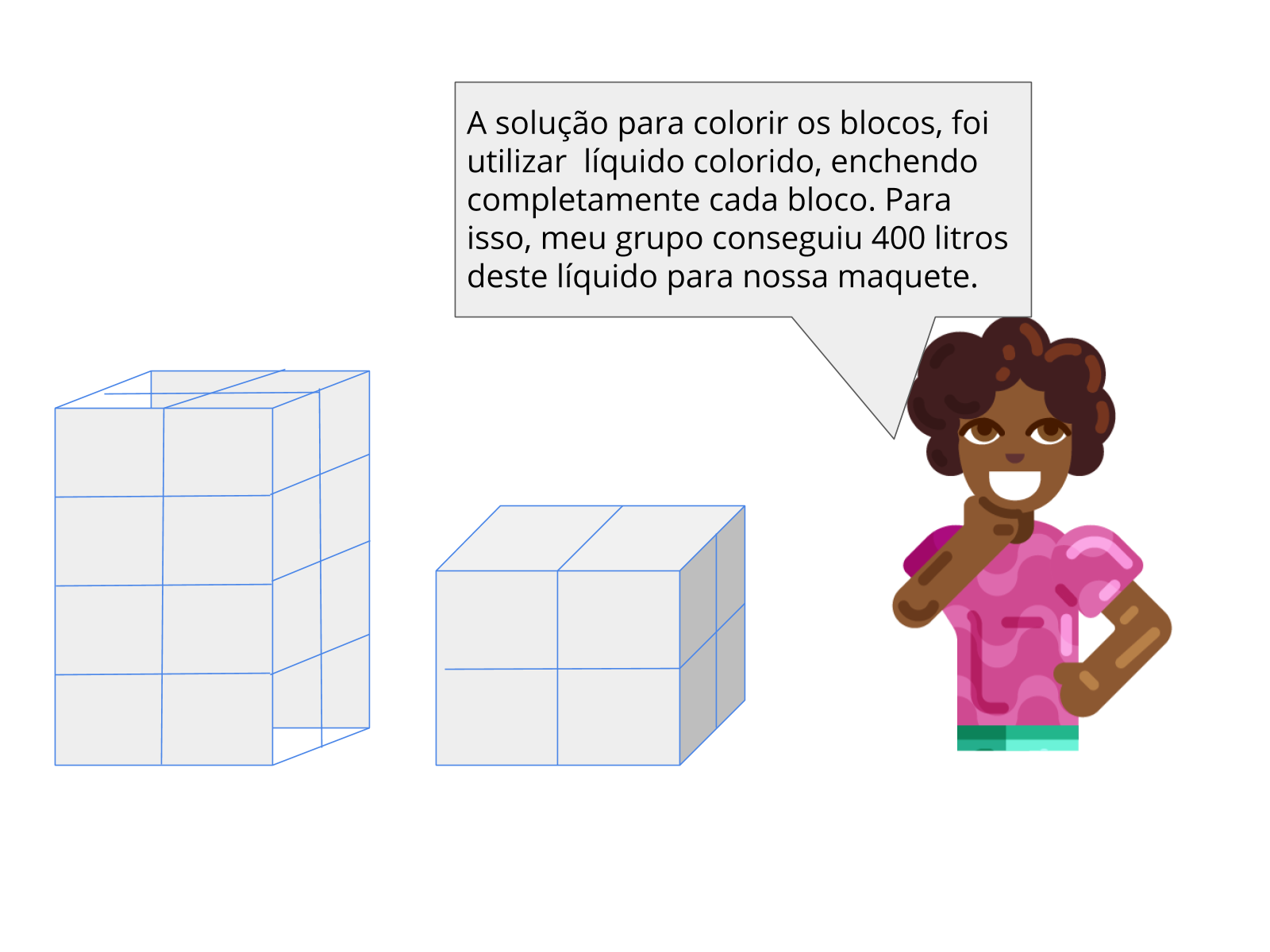
Outra consideração é que a soma dos volumes resulta em 400 dm³, volume que equivale a 400 litros. Sendo assim os valores deverão ser combinados para que as regras sejam respeitadas.
Discuta com a Turma:
- Quais as possíveis medidas dos prédios que solucionam a atividade?
- A unidade dm, que é pouco conhecida, equivalente a 10cm, ou 1 dm³ que equivale a 10cm x 10cm x 10cm, ou 1000cm³, portanto 1dm³ equivale a 1000cm³ que equivale a 1 litro.
Propósito:
- Reconhecer a relação 1dm³ equivale a 1 litro.
- Planejar possíveis medidas de paralelepípedos a partir de regras pré estabelecidas.
Atividade Principal
Tempo sugerido: 25 minutos.
Orientação:
Para resolver a situação, os alunos devem planejar a quantidade de prédios que serão utilizados, com suas respectivas dimensões, observando as regras do professor:
- 6 prédios;
- 2 deles cúbicos;
- 2 com no mínimo 4 blocos de altura.
Outra consideração é que a soma dos volumes resulta em 400 dm³, volume que equivale a 400 litros. Sendo assim os valores deverão ser combinados para que as regras sejam respeitadas.
Discuta com a Turma:
- Quais as possíveis medidas dos prédios que solucionam a atividade?
- A unidade dm, que é pouco conhecida, equivalente a 10cm, ou 1 dm³ que equivale a 10cm x 10cm x 10cm, ou 1000cm³, portanto 1dm³ equivale a 1000cm³ que equivale a 1 litro.
Propósito:
- Reconhecer a relação 1dm³ equivale a 1 litro.
- Planejar possíveis medidas de paralelepípedos a partir de regras pré estabelecidas.
Atividade Principal
Tempo sugerido: 25 minutos.
Orientação:
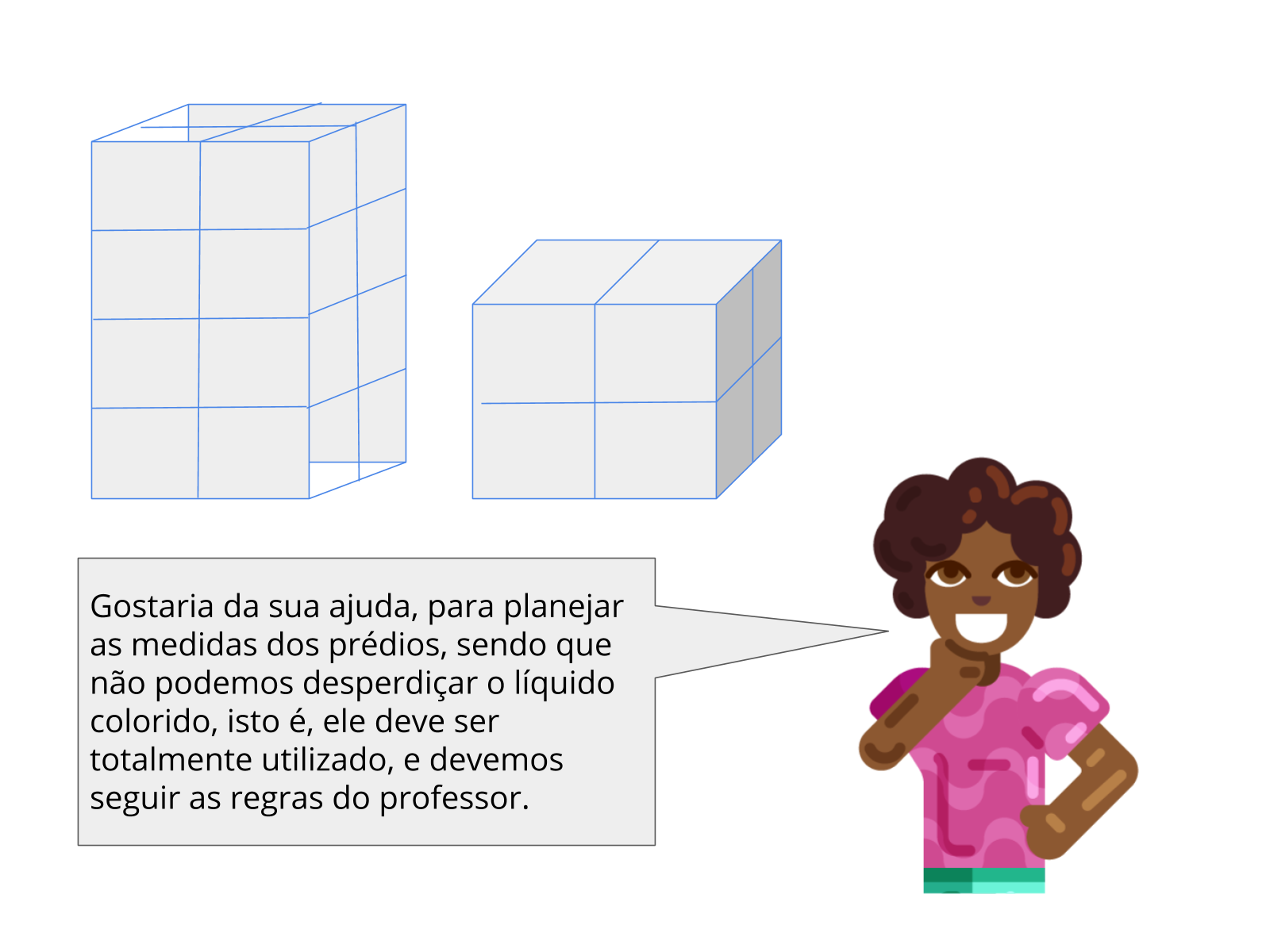
Para resolver a situação, os alunos devem planejar a quantidade de prédios que serão utilizados, com suas respectivas dimensões, observando as regras do professor:
- 6 prédios;
- 2 deles cúbicos;
- 2 com no mínimo 4 blocos de altura.
Outra consideração é que a soma dos volumes resulta em 400 dm³, volume que equivale a 400 litros. Sendo assim os valores deverão ser combinados para que as regras sejam respeitadas.
Discuta com a Turma:
- Quais as possíveis medidas dos prédios que solucionam a atividade?
- A unidade dm, que é pouco conhecida, equivalente a 10cm, ou 1 dm³ que equivale a 10cm x 10cm x 10cm, ou 1000cm³, portanto 1dm³ equivale a 1000cm³ que equivale a 1 litro.
Propósito:
- Reconhecer a relação 1dm³ equivale a 1 litro.
- Planejar possíveis medidas de paralelepípedos a partir de regras pré estabelecidas.
Painel de soluções

Tempo sugerido: 7 minutos.
Orientação: Proponha aos alunos a apresentar suas tabelas e os resultados encontrados.
Discuta com a turma:
Sabemos que cm³ se relaciona diretamente com ml, e as outras grandezas? Qual é a relação de dm³ e litro e m³ e litros?
Propósito: Reconhecer as relações entre capacidade e volume, com destaque, 1 m³ representam 1000 litros.
Painel de soluções
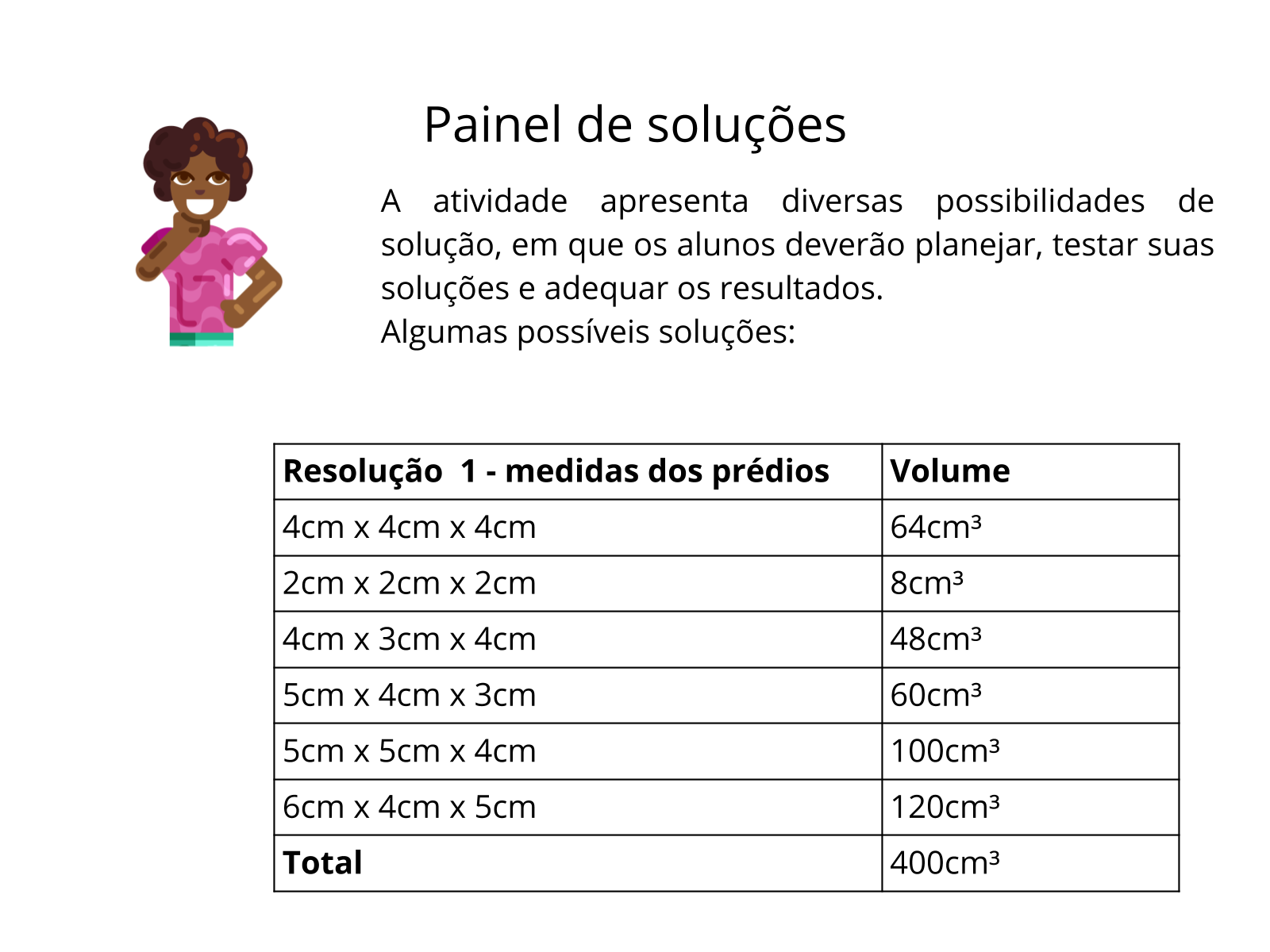
Tempo sugerido: 7 minutos.
Orientação: Proponha aos alunos a apresentar suas tabelas e os resultados encontrados.
Discuta com a turma:
Sabemos que cm³ se relaciona diretamente com ml, e as outras grandezas? Qual é a relação de dm³ e litro e m³ e litros?
Propósito: Reconhecer as relações entre capacidade e volume, com destaque, 1 m³ representam 1000 litros.
Painel de soluções

Tempo sugerido: 7 minutos.
Orientação: Proponha aos alunos a apresentar suas tabelas e os resultados encontrados.
Discuta com a turma:
Sabemos que cm³ se relaciona diretamente com ml, e as outras grandezas? Qual é a relação de dm³ e litro e m³ e litros?
Propósito: Reconhecer as relações entre capacidade e volume, com destaque, 1 m³ representam 1000 litros.
Encerramento
Tempo sugerido: 2 minutos.
Orientação: Com os resultados obtidos na atividade principal, os alunos devem relacionar as unidades de volume e capacidade.
Propósito: Reconhecer as relações entre capacidade e volume, com destaque, 1 m³ representam 1000 litros.
Raio x

Tempo sugerido: 10 minutos
Orientação:
- Os alunos devem realizar o cálculo do volume através do produtos entre as dimensões; comprimento, largura e profundidade.
- O aluno poderá ainda converter 1 m em 10 dm, considerando relação 1 dm³ = 1 litro.
- Para o cálculo do valor a ser pago pelo banco, devemos efetuar o produto da quantidade de água pelo valor por litro.
A atividade está disponível para impressão AQUI.
Resolução da atividade AQUI..
Propósito:
Resolver situação que envolve cálculo de volume e conversão de unidade de volume.
Discuta com a turma:
- Interessante questionar com os alunos, que na verdade o que se considera como comprimento, largura e profundidade, é uma questão de perspectiva, sendo que o resultado não se modificará se as dimensões forem trocadas.
- Algumas unidades de medida são pouco utilizadas nos dia-a-dia, porém elas existem, neste caso, temos o dm³ que corresponde a capacidade de 1litro.
Raio x

Tempo sugerido: 10 minutos
Orientação:
- Os alunos devem realizar o cálculo do volume através do produto entre as dimensões; comprimento, largura e profundidade.
- O aluno poderá ainda converter 1 m em 10 dm, considerando relação 1 dm³ = 1 litro.
- Para o cálculo do valor a ser pago pelo banco, devemos efetuar o produto da quantidade de água pelo valor por litro.
Propósito:
Resolver situação que envolve cálculo de volume e conversão de unidade de volume.
Discuta com a turma:
- Interessante questionar com os alunos, que na verdade o que se considera como comprimento, largura e profundidade, é uma questão de perspectiva, sendo que o resultado não se modificará se as dimensões forem trocadas.
- Algumas unidades de medida são pouco utilizadas nos dia-a-dia, porém elas existem, neste caso, temos o dm³ que corresponde a capacidade de 1litro.
Materiais complementares para impressão
Sugestão de adaptaçãoSugestão de adaptaçãopara ensino remoto
Código do plano
MAT6_19GRMO04
Recursos
- Necessários: Folha sulfite, lápis, caderno
- Opcionais: Meet, Zoom, WhatsApp, Google sala de Aula
Introdução ao volume: https://pt.khanacademy.org/math/basic-geo/basic-geo-volume-sa/volume-rect-prism/v/how-we-measure-volume
Como calcular o volume em cubos unitários decompondo uma forma: https://pt.khanacademy.org/math/pt-7-ano/grandezas-e-medidas-7ano/como-calcular-o-volume/v/volume-in-unit-cubes-by-decomposing-shape
Para este plano, foque na etapa: Atividade Principal
Atividade Principal
Você pode fazer uma sala de aula invertida. Sugira que eles assistam ao vídeo “Como calcular o volume em cubos unitários decompondo uma forma” disponível no Khan Academy. Professor, para a realização da atividade principal os alunos precisam ter acesso ao problema proposto. Para isso, tire uma foto e disponibilize a imagem no grupo de WhatsApp ou no Google Sala de Aula para que os alunos possam pensar sobre ele. Peça que tentem resolver a atividade em dois momentos. No primeiro momento eles deverão pensar sozinhos sobre a situação proposta e anotar todas as suas estratégias de cálculo no caderno. Você pode enviar a planificação do cubo para que, que quiser possam monta a torre de cubos em casa. No segundo momento, você pode sugerir que o aluno compartilhe a resposta com um familiar e juntos discutam as estratégias de resolução. Oriente-os a fotografar as suas estratégias e respostas para compartilhar com o professor e a turma no momento da discussão das soluções. Mantenha um canal de comunicação para dúvidas e esclarecimentos antes do encontro combinado.Se sua aula fora assíncrona, deixe a tarefa na escola ou envie pelo WhatsApp. Grave um áudio explicando e peçam que enviem para você combinando um retorno de devolutiva. Nesse retorno, você pode enviar o print com registros dos outros alunos para que eles comparem com suas estratégias e colem no seu caderno como repertório de soluções.
Discussão das soluções
Avalie as respostas e dúvidas apresentadas pelos alunos para dar um feedback à turma. Use informações da Sistematização do conceito para compor seu feedback. Grave um áudio ou vídeo curto (WhatsApp) para dar um ‘fechamento’ à aula. Você pode fazer um registro escrito com as principais informações e conceitos da aula para os alunos copiarem ou imprimirem. Provavelmente você terá que retomar essa aula com as atividades do Raio x e também das atividades complementares. Se sua turma dispuser de ferramentas e internet, dê preferência por realizar as discussões em tempo real, por meio de uma das plataformas sugeridas abaixo. Mas, não esqueça de manter um canal de comunicação para discussão também dessas novas atividades.
Raio X
Use o Raio X e as atividades complementares como forma de revisão para consolidação das aprendizagens. Não esqueça de retomar discussões também dessas atividades e focar nos pontos de aprendizagem mais críticos.
Convite às famílias
A participação das famílias no processo de aprendizagem é de grande importância para o aluno. Porém, ressaltamos que os pais não são professores de matemática e muitos estão ocupados com outras funções em casa. Portanto, indicamos a participação das famílias no compartilhamento e discussão de possíveis soluções para os problemas propostos.
Habilidade da BNCC
(EF06MA22) Reconhecer que o resultado de uma medida depende da unidade de medida utilizada.
Objetivos específicos
- Relacionar as medidas de capacidade (litro) e volume (dm³)
- Traçar estratégias para construção de paralelepípedos.
Conceito-chave
Medidas de volume e capacidade.
Recursos necessários
- Calculadora (caso o professor julgue necessário)
- Atividades impressas em folhas, para colar no caderno.