Resumo da aula
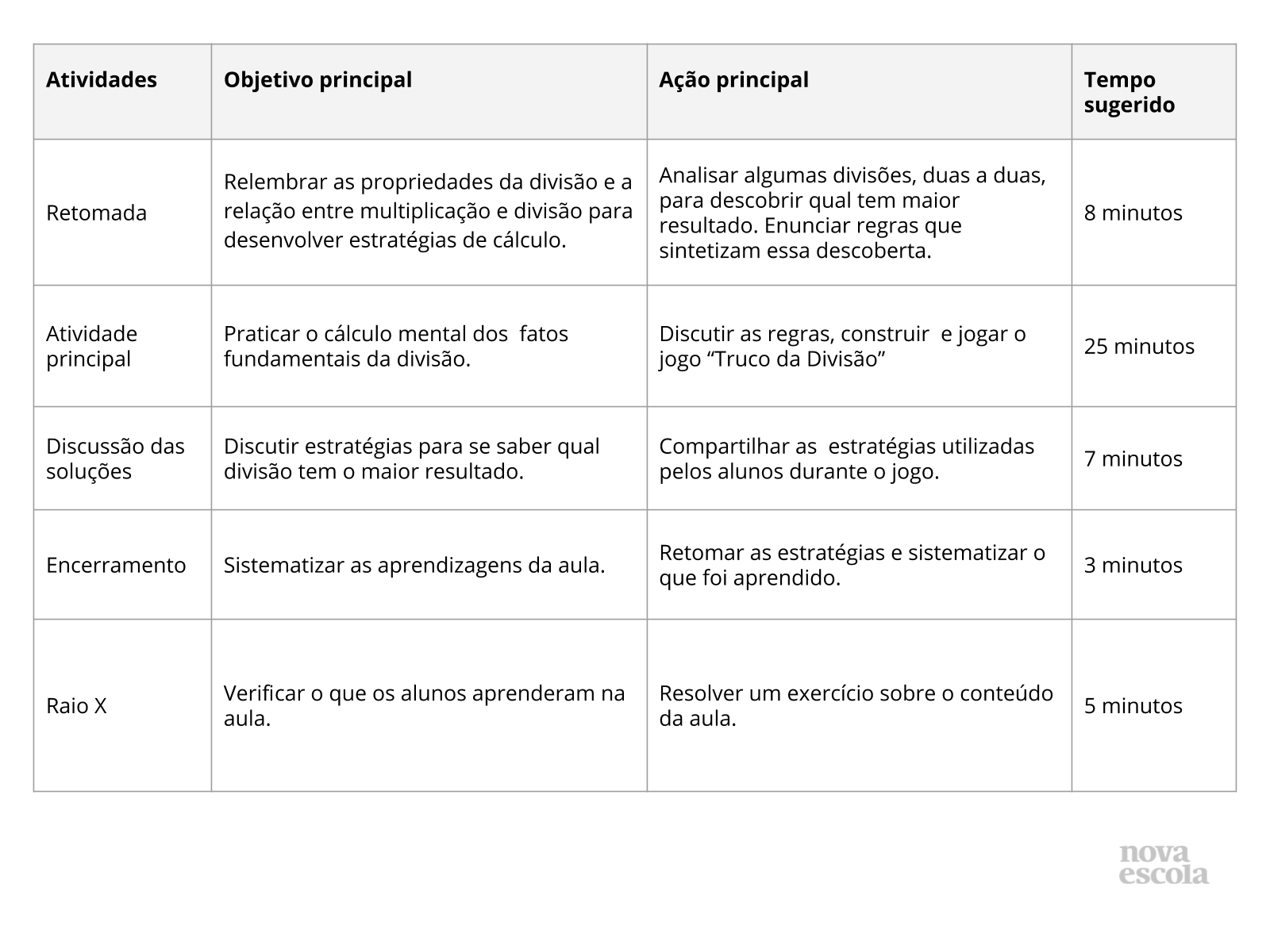
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada

Tempo sugerido: 8 minutos
Propósito: Desenvolver e justificar estratégias para encontrar qual divisão tem o maior resultado sem efetuar o cálculo.
Orientação: Projete ou escreva na lousa as duplas de divisões apresentadas nesse slide. Leia a pergunta: “Como saber qual dessas divisões tem o maior resultado?” Peça para que os alunos, individualmente, pensem sobre a pergunta por um minuto e depois, em duplas ou grupos de três, discutam suas ideias por três minutos. Abra a discussão para toda a turma e, à medida em que os alunos compartilham seu pensamento, sistematize as contribuições no quadro.
Espera-se que os alunos identifiquem qual a divisão, em cada dupla, tem o maior resultado. O foco da discussão deve ser, entretanto, estratégias para saber qual é o maior resultado sem que seja necessário fazer o cálculo, e explicações que justifiquem o uso de tais estratégias, voltando à definição da divisão e à relação da divisão e multiplicação (veja as perguntas sugeridas a seguir). Após a discussão, sistematize com os alunos uma “regra” para se identificar qual será o maior resultado no caso de os dividendos ou os divisores serem iguais. As regras serão parecidas com: “Quando os dividendos são iguais, o maior resultado será o da divisão na qual o divisor for menor” e “Quando os divisores são iguais, o maior resultado será o da divisão na qual o dividendo for maior”.
Discuta com a turma:
- Como saber qual divisão tem o maior resultado sem fazer o cálculo?
- O que significa dividir?
- Quando dividimos uma mesma quantidade por números diferentes, qual o resultado maior? (Ou transforme em um problema para melhor compreensão: Tenho 24 maçãs. Posso dividi-las entre 3 ou entre 6 pessoas. Em qual caso as pessoas receberão mais maçãs?)
- Quando dividimos diferentes quantidades por um mesmo número, qual o resultado maior? (Ou transforme em um problema para melhor compreensão: Na minha família há 4 pessoas. Quero dividir 32 balas e 20 chocolates entre todos da minha família. Cada pessoa receberá um maior número de balas ou de chocolates?)
- Sabemos que a divisão é a operação inversa da multiplicação. O número que devo multiplicar por 6 para dar 24 é maior ou menor que o número que devo multiplicar por 3 para dar 24 também?
- Sabemos que a divisão é a operação inversa da multiplicação. Nesse caso, um dos fatores é 4. O outro fator será maior na multiplicação onde o resultado é maior ou menor?
Resolução:
24 : 6 = 4 e 24 : 3 = 8 ? 24 : 3 tem o maior resultado. (Dividendos iguais, então o maior resultado será a divisão com menor divisor. Nesse caso, 24:3)
32 : 4 = 8 e 20: 4 = 5 ? 32 : 4 tem o maior resultado. (Divisores iguais, então o maior resultado será a divisão com maior dividendo. Nesse caso 32:4)
Material complementar para o professor
- Leia o capítulo 11 (Ajudando as Crianças a Dominar os Fatos Fundamentais) de VAN DE WALLE, John A. Matemática no Ensino fundamental: formação de professores e aplicação em sala de aula. Porto Alegre: Artmed, 2009.
Atividade principal
Tempo sugerido: 25 minutos
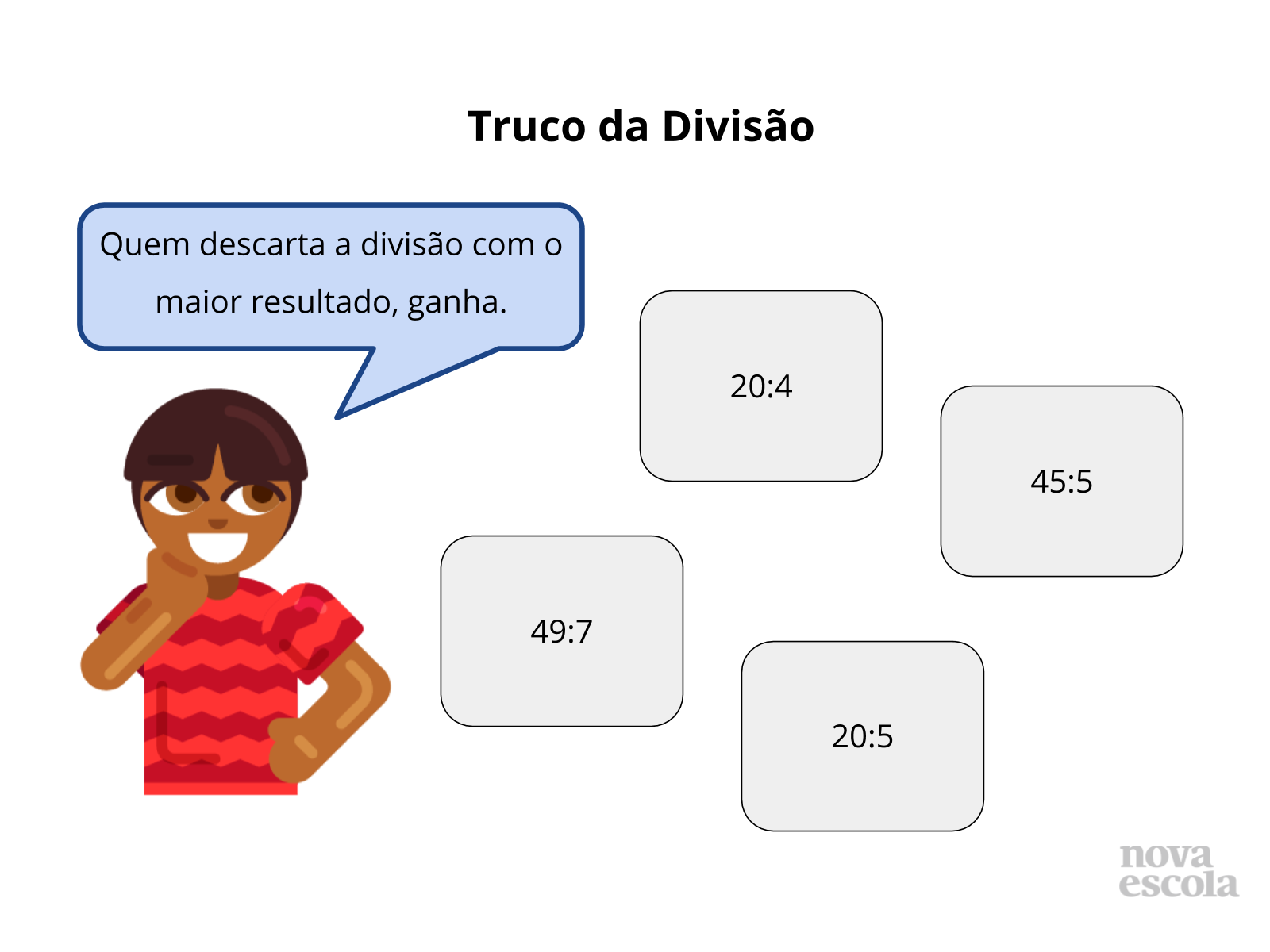
Orientação: Proponha aos alunos o jogo “Truco da Divisão”, para a prática dos fatos fundamentais da divisão, com a identificação da divisão que apresenta maior resultado. Se possível, imprima as regras e entregue para os estudantes. Leia as regras com os alunos. Caso não consiga imprimir uma cópia para cada aluno ou uma por dupla, projete, registre no quadro ou em um cartaz onde todos consigam ler. Embora o jogo de baralho “Truco” seja bastante popular, não é usualmente conhecido por essa faixa etária. É possível que alguns alunos conheçam de nome e pouco provável, mas possível que algum saiba jogar. Se esse for o caso, explique que essa será uma adaptação simplificada do jogo de baralho. As regras foram simplificadas. Após a leitura, faça uma jogada demonstrativa na lousa com 4 alunos voluntários e aproveite esse momento para esclarecer eventuais dúvidas sobre as regras e dinâmica do jogo. Os estudantes podem colar a folha com as regras, ou anotá-las, no caderno para poder jogar em outras ocasiões com amigos ou mesmo com a família.
Propósito: Compreender as regras de um jogo e discuti-las.
Discuta com a turma:
- O que vocês entenderam das regras apresentadas?
- Alguém já conhecia ou ouviu falar desse jogo?
- Alguém gostaria de propor alguma outra regra ou modificar alguma das listadas?
- Qual seria o propósito da mudança ou inclusão dessa regra?
Materiais complementares
Atividade Principal - Cartas
Atividade Principal - Regras
Resolução da Atividade Principal
Guia de intervenção
Atividade principal

Tempo sugerido: 25 minutos
Orientação: Organize duplas de jogadores e grupos de 4 alunos (duas duplas) para jogar. Se sobrar alguma dupla ou algum aluno, estes podem ficar assistindo uma partida e entrar como “próximos” na partida seguinte. Pense previamente nos grupos de forma a criar agrupamentos produtivos (leia as matérias indicadas no material complementar para o professor).
Imprima as cartas com as divisões e recorte cada carta. Use um papel mais grosso ou cole o papel da impressão em um papel mais grosso, para que as divisões não fiquem visíveis no verso das cartas. Você também pode plastificar as cartas, se esse recurso estiver disponível, para uma maior durabilidade. Essa preparação das cartas pode ser feita pelos próprios alunos em um momento anterior à aula, ou até mesmo em casa. Escolha, para o jogo, as cartas que apresentem divisões que você julgar necessárias de prática. Pode-se jogar com todas as divisões, mas isso não é imprescindível, cabendo ao professor e aos alunos decidirem quantas e quais cartas utilizar.
Proponha aos grupos que joguem o jogo independentemente. Embora a intenção seja que o cálculo seja mental, deixe disponível nas mesas papel e lápis caso algum aluno necessite escrever e, se necessário, deixe disponível a tabela de multiplicação para consulta em um primeiro momento. Enquanto os alunos jogam, circule entre eles, observando como eles jogam e calculam. Preste atenção especial a como os alunos, quando discordam em relação a um resultado, explicam suas estratégias uns aos outros. Se não explicarem, intervenha, pedindo que expliquem até que todos do grupo compreendam qual a resposta correta e como chegar nela. Em caso de dúvidas nos cálculos, peça para que conversem com os colegas para tentar resolver. Entre rodadas, converse com os alunos sobre as perguntas sugeridas abaixo. Faça anotações sobre o que observar e sobre o que os alunos falarem nesse momento.
Utilize o guia de intervenção para analisar dificuldades e realizar intervenções.
Propósito: Praticar os fatos fundamentais da divisão.
Discuta com a turma:
- Como vocês pensaram para saber qual resultado é maior?
- Essa estratégia funciona para todos os conjuntos de divisões?
- Vocês já discordaram sobre qual era o maior resultado em alguma rodada?
- Se sim, como resolveram essa discordância?
- Vocês estão compartilhando estratégias?
- Quem aprendeu alguma estratégia nova com um colega?
- Quais as dificuldades que apareceram?
- Como as dificuldades foram resolvidas?
- Você já está mais seguro com os resultados de alguma divisão que julgava mais difícil?
Materiais complementares
Atividade Principal - Cartas
Atividade Principal - Regras
Resolução da Atividade Principal
Guia de intervenção
Material complementar para o professor:
Discussão da solução

Tempo sugerido: 7 minutos
Orientação: Converse com os alunos sobre quais estratégias eles utilizaram para saber qual resultado era maior.Peça que compartilhem estratégias usadas durante o jogo para a identificação da divisão com maior resultado. Peça que 3 ou 4 alunos compartilhem como resolveram as dificuldades ou como um colega lhe explicou os possíveis equívocos. Pergunte se alguém usou diferentes estratégias dependendo dos números envolvidos. Peça que compartilhem. Nesse momento, retome as anotações que você fez durante a observação do jogo e convide alunos específicos a compartilharem suas estratégias e dificuldades, de acordo com o que foi observado. Dessa forma, haverá uma variedade a ser discutida. Anote os nomes dos alunos que compartilharam suas resoluções próximo ao registro da estratégia. Se possível, deixe esse registro exposto na sala.
Propósito: Discutir estratégias para se saber qual divisão tem o maior resultado.
Discuta com a turma:
- Quais estratégias você utilizou durante o jogo?
- A estratégia que você encontrou foi bem sucedida?
- O que você aprendeu com a sua estratégia?
- Em que situação cada estratégia foi mais utilizada?
- Quais as dificuldades que apareceram?
- Como as dificuldades foram resolvidas?
- Quais os fatos fundamentais que vocês já dominam?
- Quais ainda necessitam mais tempo para saber o resultado?
Encerramento
Tempo sugerido: 3 minutos
Orientações: Encerre a atividade retomando com os estudantes as atividades feitas nesta aula e o que foi aprendido. Retome com os alunos as estratégias elencadas por eles e converse sobre quando é possível utilizá-las e quando é necessário realizar os cálculos para poder comparar os resultados. Anote as contribuições na lousa, de forma que fiquem visíveis para todos.
Propósito: Sistematizar a aprendizagem, revisando o que foi estudado.
Discuta com a turma:
- O que fizemos nessa aula?
- O que aprendemos ou praticamos nessa aula?
- Quais estratégias conhecemos para comparar resultados de divisões?
- Quando essas estratégias podem ou não ser utilizadas?
- Como sabemos qual o maior resultado quando não podemos utilizar essas estratégias?
Raio X

Tempo sugerido: 5 minutos.
Orientações: Para finalizar a aula, apresente o exercício para os alunos. Você poderá projetá-lo ou imprimi-lo. Peça aos alunos que leiam e resolvam individualmente. Circule para verificar como os alunos estão realizando a atividade. O Raio X é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. No final, reserve um tempo para um debate coletivo registrando as soluções no quadro.
Propósito: Verificar o que os alunos aprenderam na aula.
Discuta com a turma:
- Sobre o que foi a nossa aula hoje?
- O que você aprendeu com ela?
- Em que parte você sentiu mais dificuldade? Como conseguiu superá-la?
- Quais estratégias vocês usaram para descobrir qual era o maior resultado?
- Qual estratégia podemos utilizar para descobrir qual resultado de divisão é maior sem calcular todas as divisões?
Materiais complementares:
Raio X
Resolução do raio x
Atividade complementar
Resolução da atividade complementar
Material de Apoio
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. 
















