Atividade Principal 1
Plano de Aula
Plano de aula: Estimar a ordem de grandeza do quociente.
Plano 4 de uma sequência de 5 planos. Veja todos os planos sobre Estimativa de quocientes
Por: Isabel Cossalter
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Isabel Cossalter
Mentor: Elisa Greenhalgh Vilalta
Especialista de área: Luciana Tenuta
Habilidade da BNCC
EF04MA04 - Utilizar as relações entre adição e subtração, bem como entre multiplicação e divisão, para ampliar as estratégias de cálculo.
Objetivos específicos
Explorar estratégias de cálculo para estimar a ordem de grandeza de um quociente.
Conceito-chave
Estimativa da ordem de grandeza de um quociente.
Recursos necessários
- Folha de papel A4 branca.
- Fichas com as cartelas do jogo.
- Lápis e borracha.
- Lousa e giz.
Habilidades BNCC:
Objetivos de aprendizagem
Explorar estratégias de cálculo para estimar a ordem de grandeza de um quociente.
Resumo da aula
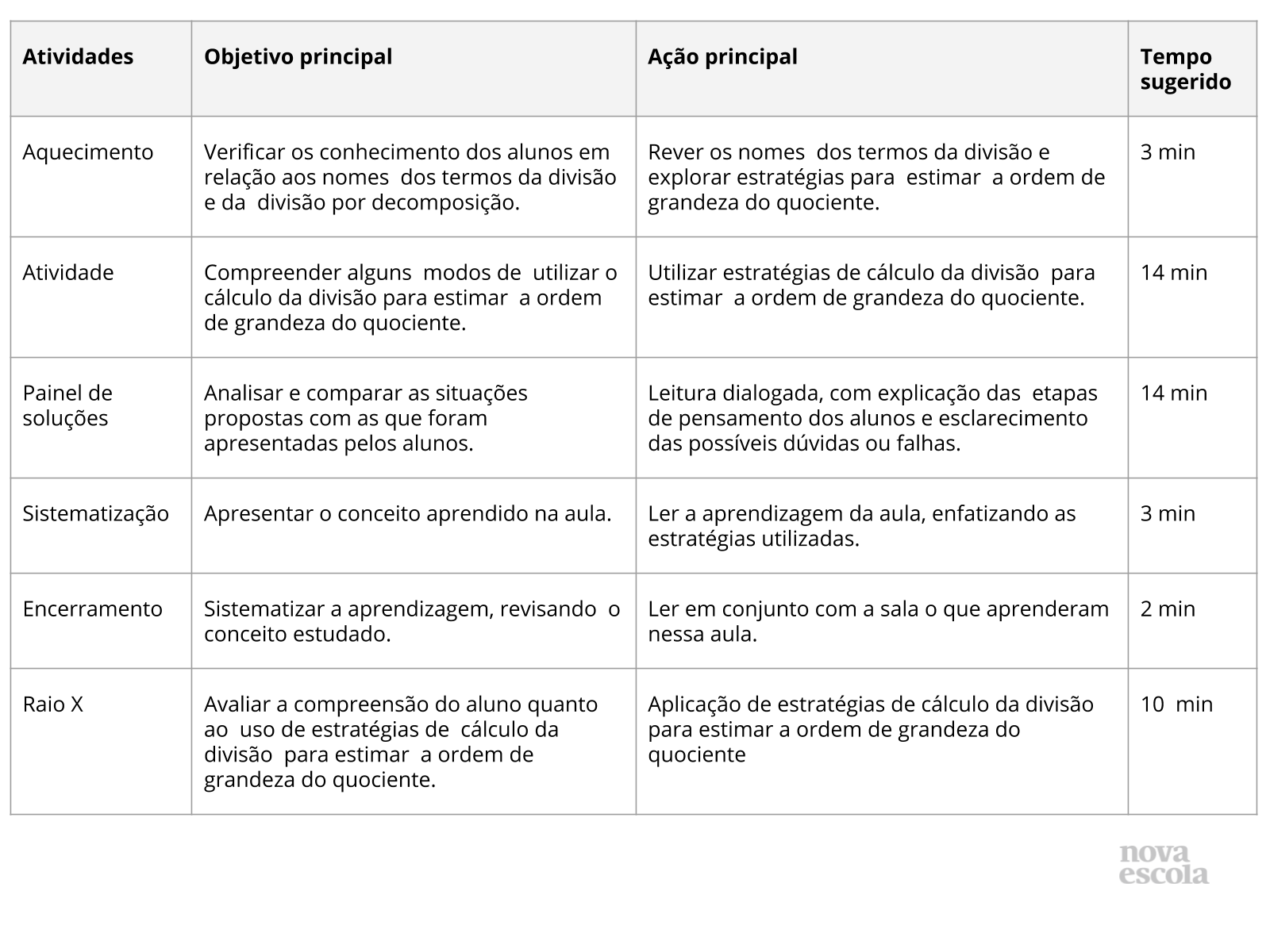 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos
Propósito: Utilizar estratégias de cálculo da divisão para estimar a ordem de grandeza do quociente.
Orientação: Leia para a classe ou peça a um aluno que leia o slide em voz alta.
Discuta com a turma:
- Como podemos calcular por decomposição?
- Como podemos fazer uma operação de divisão por decomposição?
- Ordem de grandeza do quociente. Quem sabe o que é isso?
Respostas possíveis:
- Sei que 7 x 8 = 56, isso quer dizer que 7 x 80 = 560. Cada prestação será de R$80,00 ,portanto, não chegará a 1 centena.
- 560 tem apenas 5 centenas, não há centenas suficientes para dividir por 7.
Aquecimento

Tempo sugerido: 3 minutos
Propósito: Rever os nomes dos termos da divisão e explorar estratégias para estimar a ordem de grandeza do quociente.
Orientação: Leia para a classe ou peça a alguns alunos que leiam as falas do garoto em voz alta. Faça pequenas paradas durante a leitura para se certificar de que as crianças estão compreendendo adequadamente a situação proposta. Chame a atenção de todos para os dados do cartaz da loja de bicicleta e para a condição colocada pelo pai do garoto para realizar a compra. Solicite que expliquem o que o pai respondeu a Daniel quando ele achou que ele não poderia comprar a bicicleta.
Discuta com a turma:
- No cartaz da loja há uma operação matemática. Qual? Como podemos representá-la?
- Quem se lembra dos nomes dos termos da divisão?
- O pai do Daniel disse “o quociente dessa divisão não terá centenas”. O que é quociente? De qual divisão ele estava falando?
- Quem consegue responder a pergunta feita por Daniel? Como o pai percebeu que o quociente não teria centenas?
Respostas possíveis:
- Sei que 7 x 8 = 56, isso quer dizer que 7 x 80 = 560. Cada prestação será de R$80,00 ,portanto, não chegará a 1 centena.
- 560 tem apenas 5 centenas, não há centenas suficientes para dividir por 7.
Aquecimento

Tempo sugerido: 3 minutos
Propósito: Rever os nomes dos termos da divisão e explorar estratégias para estimar a ordem de grandeza do quociente.
Orientação: Leia para a classe ou peça a alguns alunos que leiam as falas do garoto em voz alta. Faça pequenas paradas durante a leitura para se certificar de que as crianças estão compreendendo adequadamente a situação proposta. Chame a atenção de todos para os dados do cartaz da loja de bicicleta e para a condição colocada pelo pai do garoto para que pudesse realizar a compra. Solicite que expliquem o que o pai respondeu a Daniel quando ele achou que o pai não poderia comprar a bicicleta.
Discuta com a turma:
- No cartaz da loja há uma operação matemática. Qual? Como podemos representá-la?
- Quem se lembra dos nomes dos termos da divisão?
- O pai do Daniel disse “o quociente dessa divisão não terá centenas”. O que é quociente? De qual divisão ele estava falando?
- Quem consegue responder a pergunta feita por Daniel? Como o pai percebeu que o quociente não teria centenas?
Respostas possíveis:
- Sei que 7 x 8 = 56, isso quer dizer que 7 x 80 = 560. Cada prestação será de R$ 80,00, portanto, não chegará a 1 centena.
- 560 tem apenas 5 centenas e a divisão é por 7, seriam necessárias 7 centenas para dividir por 7 para que quociente tivesse 1 centena.
Atividade principal

Tempo sugerido: 14 minutos
Propósito: Estimar a ordem de grandeza de um quociente.
Orientação: Monte grupos de três ou quatro alunos, que possam cooperar entre si durante a atividade. Faça uma leitura compartilhada das regras do jogo. Esclareça que o objetivo do trabalho é treinar maneiras de estimar o quociente e não apenas responder V ou F. Por isso, peça que caprichem nas estratégias e nas justificativas. Dê aproximadamente 7 minutos para a realização da tarefa. Encerrado o tempo de trabalho, vá fazendo a correção coletiva e atribuindo pontos aos grupos. Estimule as crianças a elaborarem junto com os colegas na última questão do jogo. Após socializar as questões, se possível, envie-as para serem realizadas como lição de casa.
Discuta com a turma:
- O que acharam de estimar o quociente pensando nas ordens dos algarismos?
- Ao estimar um quociente, considerar a quantidade de algarismos que ele terá, ajuda a evitar erros? Por quê?
- Há mais de uma forma de fazer isso, certo? Quais vocês podem citar?
- Alguém tem alguma dica para dar aos colegas, que possa ajudar na hora de estimar a ordem de grandeza do quociente?
- Foi fácil ou difícil elaborar a última questão do jogo? Por quê?
Material de apoio para o professor
- Leia a matéria “ Aprender divisão é mais que dividir”, sobre o ensino do conceito de divisão, de 2016, aqui:
https://novaescola.org.br/conteudo/71/como-ensinar-operacoes-de-multiplicacao-e-divisao
Materiais complementares para impressão:
Atividade principal

Tempo sugerido: 14 minutos
Propósito: Estimar a ordem de grandeza de um quociente.
Orientação: Faça uma leitura compartilhada das regras do jogo. Esclareça que o objetivo do trabalho é treinar maneiras de estimar o quociente e não apenas responder V ou F. Por isso, peça que caprichem nas estratégias e nas justificativas. Organize grupos de alunos que possam cooperar entre si durante a atividade. Dê aproximadamente 7 minutos para a realização da tarefa. Encerrado o tempo de trabalho, vá fazendo a correção coletiva e atribuindo pontos aos grupos. Estimule as crianças a elaborarem junto com os colegas na última questão do jogo. Após socializar as questões elaboradas, se possível, envie-as para serem realizadas como lição de casa.
Discuta com a turma:
- O que acharam de estimar o quociente pensando nas ordens dos algarismos?
- Ao estimar um quociente, considerar a quantidade de algarismos que ele terá, ajuda a evitar erros? Por quê?
- Há mais de uma forma de fazer isso, certo? Quais vocês podem citar?
- Alguém tem alguma dica para dar aos colegas, que possa ajudar na hora de estimar a ordem de grandeza do quociente?
- Foi fácil ou difícil elaborar a última questão do jogo? Por quê?
Discussão da solução
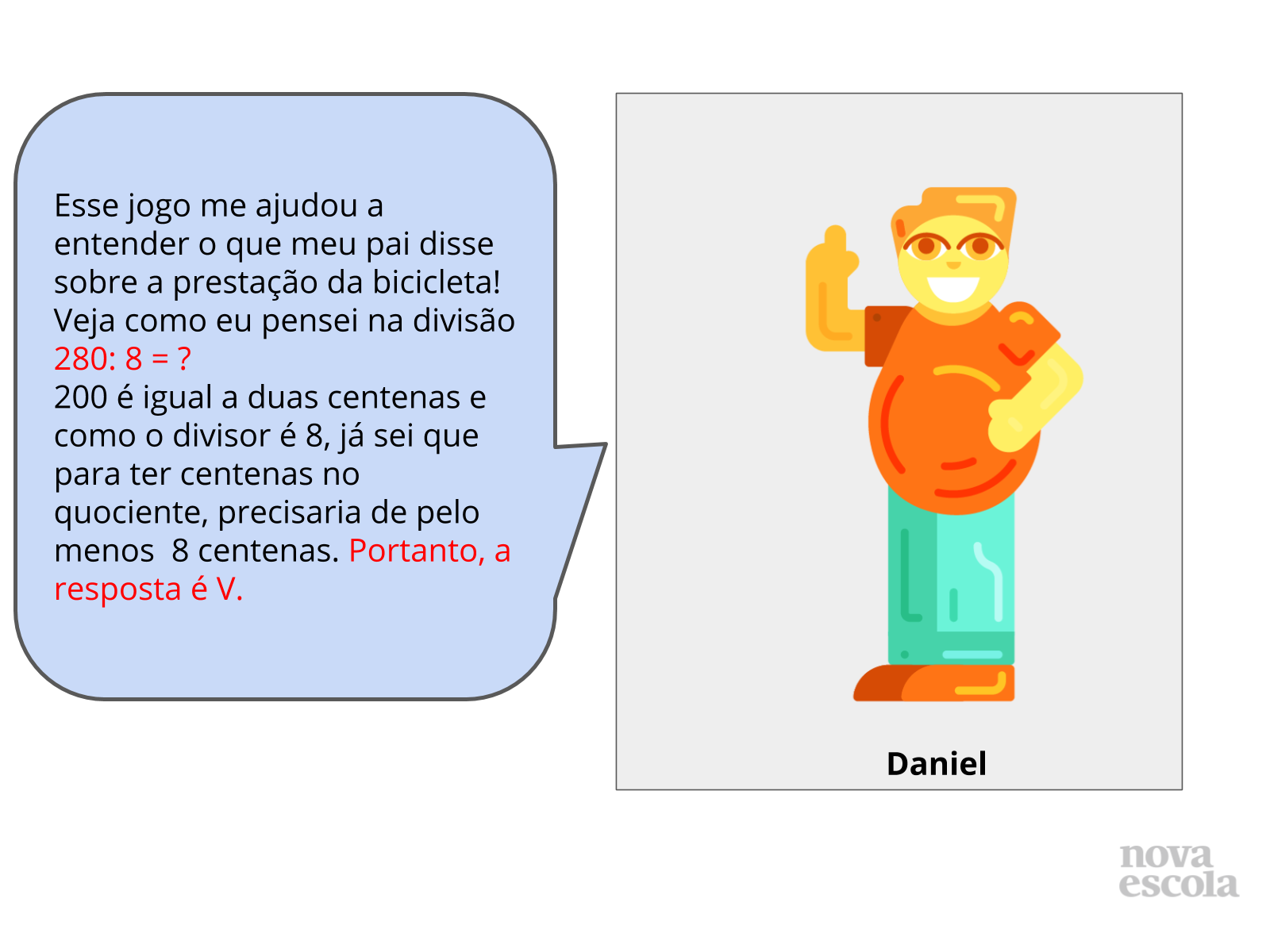
Tempo sugerido: 14 minutos
Propósito: Discutir formas de estimar a ordem de grandeza de um quociente.
Orientação: Leia as falas de Daniel e Roberta para a turma ou peça a dois alunos que o façam em voz alta. A partir das estratégias apresentadas nos slides, amplie a discussão com a classe procurando enfatizar os raciocínios matemáticos utilizados pelos grupos ao estimar os quocientes. Deixe que expliquem aos colegas como pensaram de compare os procedimentos apresentados. Se considerar adequado, faça um registro da discussão e monte um cartaz que possa ficar no painel da sala e servir como fonte de consulta para os alunos.
Discuta com a turma:
- Levar em conta as ordens dos algarismos é uma maneira eficiente de estimar o quociente? Por quê?
- Considerar a quantidade de algarismos do quociente ao fazer uma estimativa ajuda a evitar erros? Por quê?
- Dos procedimentos apresentados hoje, qual vocês usaram mais? Qual acharam mais prático? Qual é mais fácil de compreender?
- Agora que já fizemos vários exercícios, quem poderia explicar o que significa “estimar a ordem de grandeza do quociente”? O que é “ordem de grandeza”?
- Em quais situações do dia a dia pode ser interessante saber estimar a ordem de grandeza de um quociente? Dê exemplos.
Discussão da solução

Tempo sugerido: 14 minutos
Propósito: Discutir formas de estimar a ordem de grandeza de um quociente.
Orientação: Leia as falas de Daniel e Roberta para a turma ou peça a dois alunos que o façam em voz alta. A partir das estratégias apresentadas nos slides, amplie a discussão com a classe procurando enfatizar os raciocínios matemáticos utilizados pelos grupos ao estimar os quocientes. Deixe que expliquem aos colegas como pensaram de compare os procedimentos apresentados. Se considerar adequado, faça um registro da discussão e monte um cartaz que possa ficar no painel da sala e servir como fonte de consulta para os alunos.
Discuta com a turma:
- Levar em conta as ordens dos algarismos é uma maneira eficiente de estimar o quociente? Por quê?
- Considerar a quantidade de algarismos do quociente ao fazer uma estimativa ajuda a evitar erros? Por quê?
- Dos procedimentos apresentados hoje, qual vocês usaram mais? Qual acharam mais prático? Qual é mais fácil de compreender?
- Agora que já fizemos vários exercícios, quem poderia explicar o que significa “estimar a ordem de grandeza do quociente”? O que é “ ordem de grandeza”?
- Em quais situações do dia a dia pode ser interessante saber estimar a ordem de grandeza de um quociente? Dê exemplos.
Sistematização

Tempo sugerido: 3 minutos
Propósito: Sistematizar o conceito de ordem de grandeza de um quociente.
Orientação: Faça uma leitura compartilhada do slide com os alunos. Relembre com eles o início da aula (a dúvida apresentada por Daniel na loja de bicicletas e a resposta do seu pai) e esclareça dúvidas.
Discuta com a turma:
- Todos se lembram da dúvida apresentada por Daniel no início da nossa aula?
- Como a dúvida dele a resposta dada pelo seu pai se relacionam ao tema da aula de hoje?
- Quem poderia explicar para a classe, com palavras diferentes das usadas no slide, o que significa “estimar a ordem de grandeza de um quociente”?
Encerramento

Tempo sugerido: 2 minutos
Propósito: Resumir os conteúdos abordados na aula para organizar o pensamento das crianças.
Orientação: Faça uma leitura compartilhada do slide com os alunos.
Discuta com a turma:
- Ainda há dúvidas sobre a aula de hoje?
- Quem poderia fazer um breve resumo do que aprendemos?
- Alguém poderia dar um exemplo da utilidade do cálculo por estimativa da ordem de grandeza do quociente?
Raio X
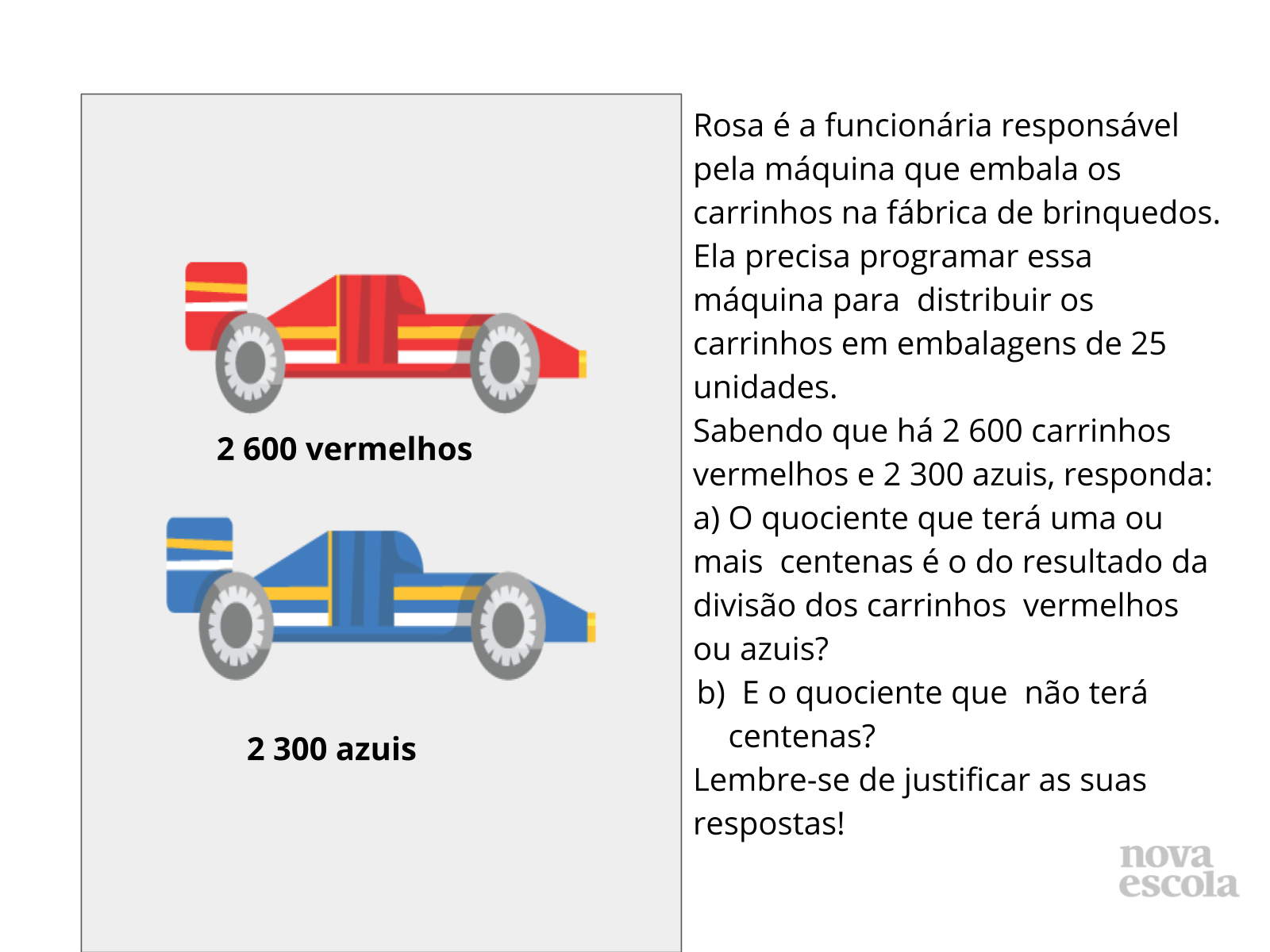
Tempo sugerido: 10 minutos
Propósito: Estimar a ordem de grandeza do quociente.
Orientação: Faça uma leitura compartilhada do enunciado do problema para garantir que todos compreenderam a atividade a ser feita. Peça aos alunos que verbalizem as orientações dadas e as expliquem com as próprias palavras. Se necessário, relembre as estratégias usadas na atividade principal. Solicite às crianças que realizem a tarefa individualmente. Circule pela sala, observe as estratégias utilizadas pelas crianças e verifique se estão conseguindo resolver o problema proposto. Se surgirem dúvidas, procure esclarecê-las sem interferir no trabalho do aluno, pois esse é um momento de avaliação e é importante que possamos perceber possíveis erros e acertos, tanto do aluno quanto no encaminhamento das discussões.Reserve pelo menos 5 minutos para conversar sobre a estratégias e raciocínios usados pelas crianças para resolver a atividade.
Discuta com a turma:
- Vocês conseguiram estimar a ordem de grandeza dos quocientes? Quem não conseguiu? Vamos verificar o que aconteceu?
- Como se sentiram ao realizar a atividade individualmente?
- Quais foram as dificuldades? Foi possível resolvê-las? Como fizeram?
- Tivemos resultados diferentes? Por que isso aconteceu?
- Houve alguma estratégia de cálculo que foi mais eficiente para a resolução desse problema?
Materiais complementares para impressão:
Sugestão de adaptação para ensino remoto
Código do plano
MAT4_07NUM_04
Recursos
USAR APENAS FERRAMENTAS EM PORTUGUÊS E GRATUITAS
- Necessários: -
- Opcionais: FlipGrid, Google Meet, Google Formulários, WhatsApp, Google Apresentações.
Para este plano, foque na etapa Atividade Principal.
Aquecimento
Propor para a turma a pergunta do Daniel e pedir que indiquem suas respostas, o que pode ser feito por Google Meet (síncrono) ou FlipGrid (assíncrono), sendo que nesse último eles gravariam um vídeo curto explicando o que pensaram para a solução antes de partir para as atividades do plano. Sem os recursos digitais, o professor pode pedir o registro escrito dessas questões, lembrando de incluir as questões presentes nas orientações ao professor aqui.
Atividade principal
Transpor as questões de “verdadeiro ou falso” do jogo presente nesta etapa para o Google Formulários ampliando o número de questões (sugerimos dobrar esse número) e solicitar que resolvam o mais rápido possível. Após a resolução o professor consegue comparar o tempo de resolução dos alunos e o número de acertos. Sem o recurso digital, o professor pode propor que os alunos resolvam as questões apresentadas e, após uma devolutiva, criem outras possíveis para o professor enviar aos demais colegas.
Discussão das soluções
Propor que os alunos identifiquem as vantagens e desvantagens de cada uma das formas de calcular aqui apresentadas. Isso pode ser feito por escrito ou via Google Formulários.
Sistematização
O professor pode sistematizar o que foi estudado aqui a partir de uma sequência de slides que contemplem a ideia e mais um exemplo relacionado ao conceito, usando o Google Apresentações ou enviando um registro escrito disso. Unir essa etapa à próxima (Encerramento).
Encerramento
Ver orientação da etapa anterior.
Raio X
Além de resolver, pedir que os alunos façam um registro explicando como pensaram ou como explicariam o que pensaram para um colega.
É possível solicitar registro escrito ou a gravação de um vídeo para envio via WhatsApp.
Convite às famílias
Convidar a família a jogar o jogo da atividade principal no formato original com os alunos.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Isabel Cossalter
Mentor: Elisa Greenhalgh Vilalta
Especialista de área: Luciana Tenuta
Habilidade da BNCC
EF04MA04 - Utilizar as relações entre adição e subtração, bem como entre multiplicação e divisão, para ampliar as estratégias de cálculo.
Objetivos específicos
Explorar estratégias de cálculo para estimar a ordem de grandeza de um quociente.
Conceito-chave
Estimativa da ordem de grandeza de um quociente.
Recursos necessários
- Folha de papel A4 branca.
- Fichas com as cartelas do jogo.
- Lápis e borracha.
- Lousa e giz.










