Resumo da Aula
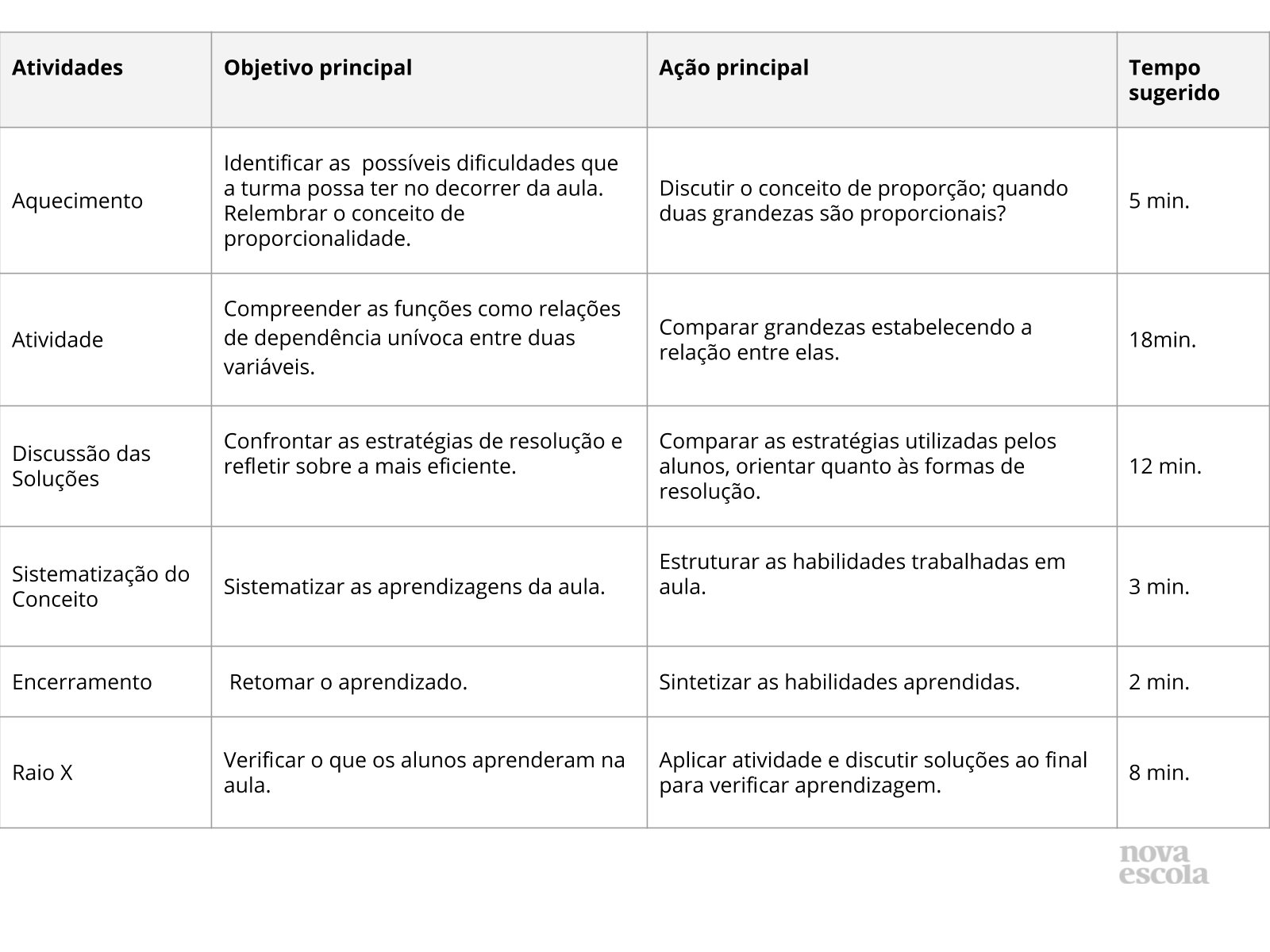
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Leia ou projete o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Aquecimento

Tempo sugerido: 5 minutos.
Orientação: Proponha à turma um rápido debate para relembrar os conceitos.
Discuta com a turma:
- O que são grandezas?
- Como definir se existe relação entre duas grandezas?
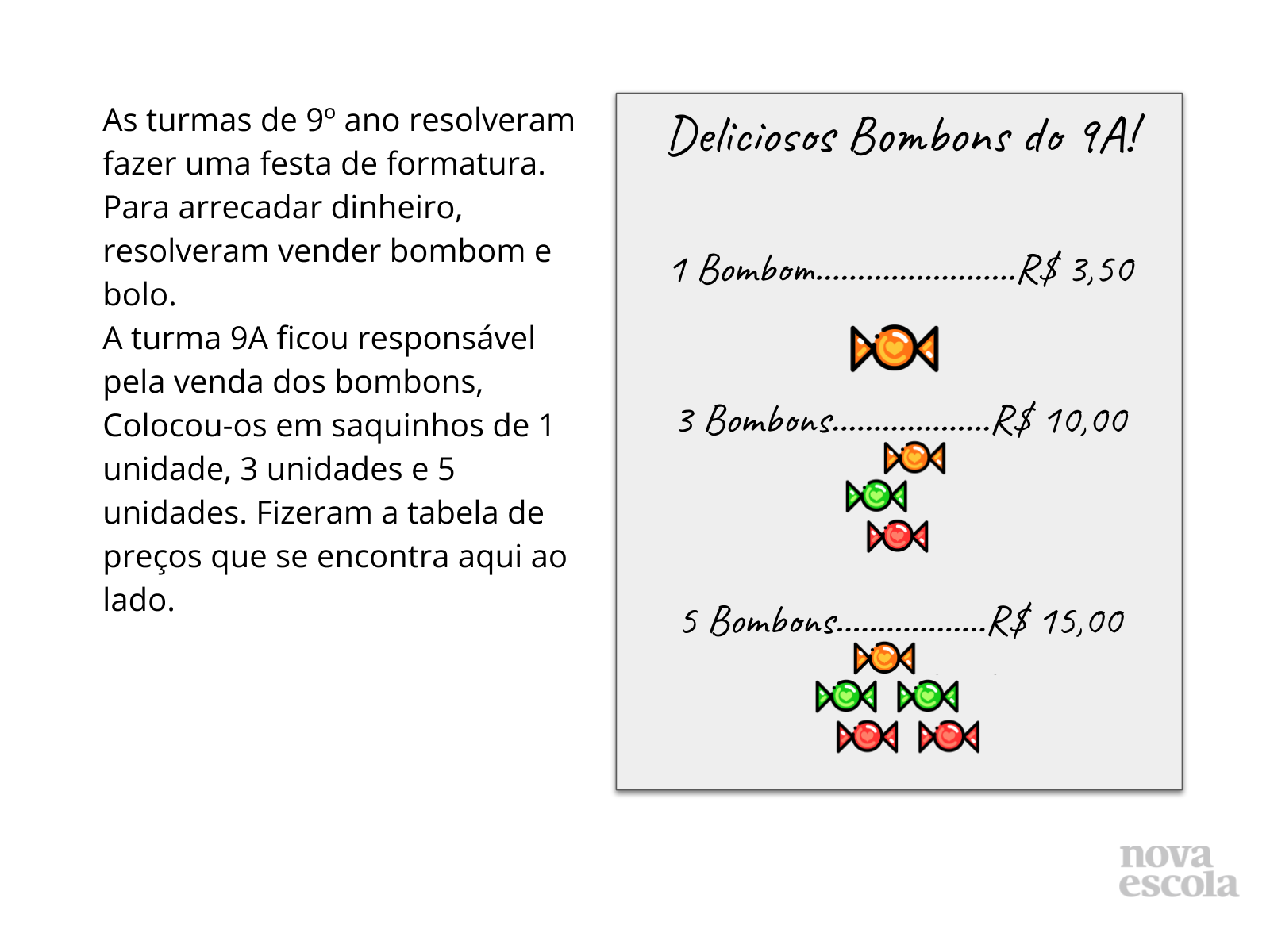
Atividade Principal
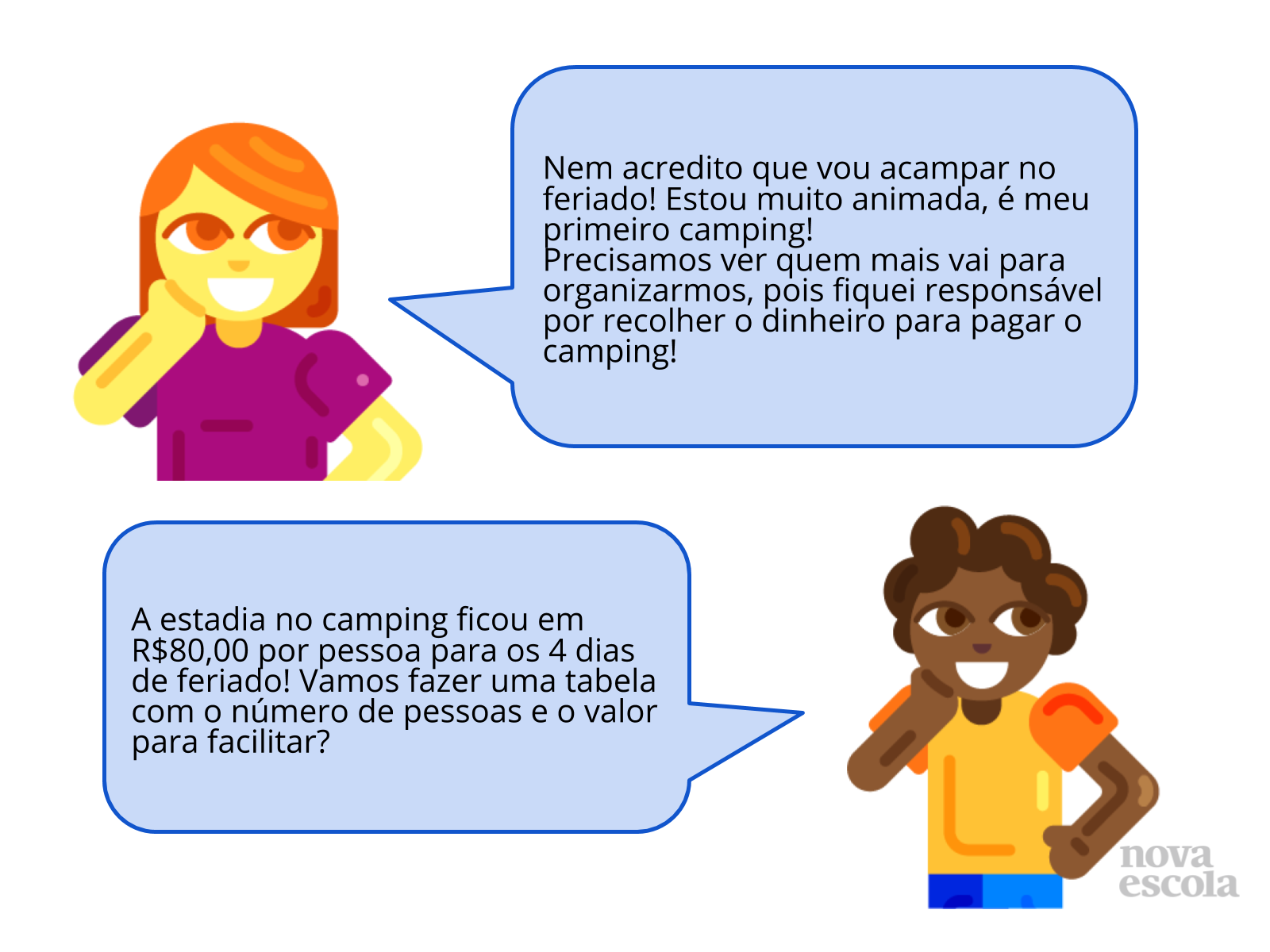
Tempo sugerido: 18 minutos. (Slides 4 a 6).
Orientação: No primeiro momento, peça para os alunos pensarem nas soluções individualmente. Depois, em duplas, peça para que comparem as respectivas soluções.
Propósito: Compreender as funções como relações de dependência unívoca entre duas variáveis.
Discuta com a turma:
- Existe relação entre o valor e número de pessoas?
- É possível que, com uma quantidade diferente de pessoas, o valor final seja o mesmo?
- Por que é importante generalizar, escrevendo a fórmula?
- A matemática pode ser uma ferramenta para resolver problemas do cotidiano?
Material complementar:
Atividade principal
Resolução da atividade
Guia de intervenção
Acessando este link você encontra mais sobre o assunto.
Atividade Principal

Tempo sugerido: 18 minutos. (Slides 4 a 6).
Orientação: No primeiro momento, peça para os alunos pensarem nas soluções individualmente. Depois, em duplas, peça para que comparem as respectivas soluções.
Propósito: Compreender as funções como relações de dependência unívoca entre duas variáveis.
Discuta com a turma:
- Existe relação entre o valor e número de pessoas?
- É possível que, com uma quantidade diferente de pessoas, o valor final seja o mesmo?
- Por que é importante generalizar, escrevendo a fórmula?
- A matemática pode ser uma ferramenta para resolver problemas do cotidiano?
Atividade Principal
Tempo sugerido: 18 minutos. (Slides 4 a 6).
Orientação: No primeiro momento, peça para os alunos pensarem nas soluções individualmente. Depois, em duplas, peça para que comparem as respectivas soluções.
Propósito: Compreender as funções como relações de dependência unívoca entre duas variáveis.
Discuta com a turma:
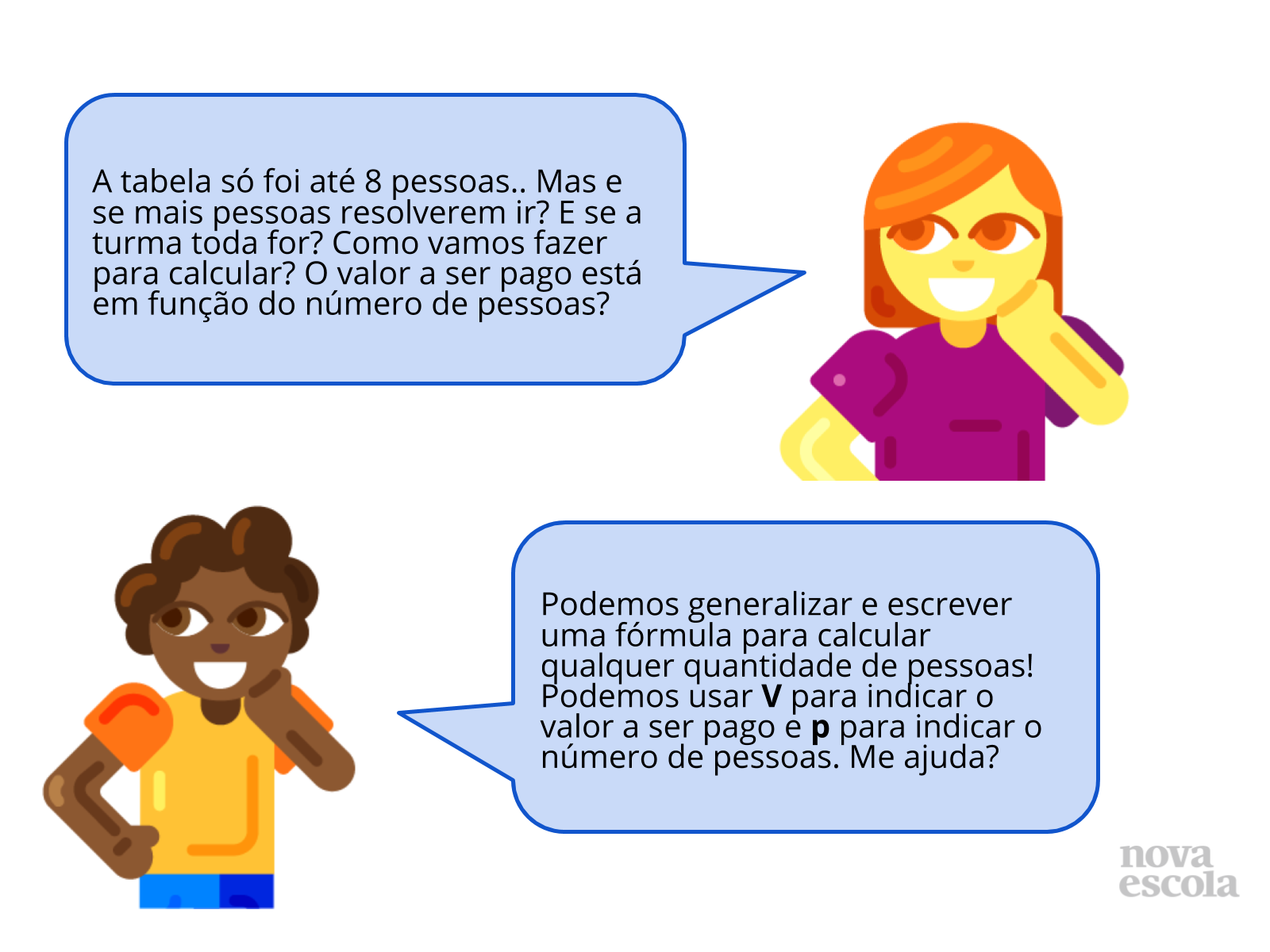
- Existe relação entre o valor e número de pessoas?
- É possível que, com uma quantidade diferente de pessoas, o valor final seja o mesmo?
- Por que é importante generalizar, escrevendo a fórmula?
Discussão das Soluções

Orientações: Peça a turma que compartilhe as soluções alcançadas. Lembre-se sempre de incentivar a criatividade e autonomia de pensamento do seu aluno. Caso seja necessário, utilize a sequência de slides a seguir.
Propósito: Explorar as diversas formas de solução pensadas pelos alunos.
Discuta com a turma:
- Qual a relação existente entre o número de pessoas e o valor total a ser pago?
Discussão das Soluções

Orientações: Peça a turma que compartilhe as soluções alcançadas. Lembre-se sempre de incentivar a criatividade e autonomia de pensamento do seu aluno. Caso seja necessário, utilize a sequência de slides a seguir.
Propósito: Explorar as diversas formas de solução pensadas pelos alunos.
Discuta com a turma:
- Qual a relação existente entre o número de pessoas e o valor total a ser pago?
Discussão das Soluções

Orientações: Peça a turma que compartilhe as soluções alcançadas. Lembre-se sempre de incentivar a criatividade e autonomia de pensamento do seu aluno. Caso seja necessário, utilize a sequência de slides a seguir.
Propósito: Explorar as diversas formas de solução pensadas pelos alunos.
Discuta com a turma:
- Qual a relação existente entre o número de pessoas e o valor total a ser pago?
Discussão das Soluções

Orientações: Peça a turma que compartilhe as soluções alcançadas. Lembre-se sempre de incentivar a criatividade e autonomia de pensamento do seu aluno. Caso seja necessário, utilize a sequência de slides a seguir.
Propósito: Explorar as diversas formas de solução pensadas pelos alunos.
Discuta com a turma:
- Qual a relação existente entre o número de pessoas e o valor total a ser pago?
Sistematização dos Conceitos

Orientação: Para encerrar a aula, retome o que foi discutido. Sintetize cada um dos ítens acima.
Propósito: Sistematizar as aprendizagens da aula
Discuta com a turma
- Na generalização y=a.x, o que significam as letras x, y e a ?
Encerramento

Tempo sugerido: 2 minutos.
Orientações: Para encerrar a aula, retome o que foi discutido.
Propósito: Retomar o aprendizado.
RAIO X

Tempo sugerido: 8 minutos. (Slides de 13 a 17).
Orientação: Peça que os alunos realizem a atividade individualmente.
Propósito: Verificar aprendizagem.
Discuta com a turma:
- Qual a variável dependente na função? E a independente?
RAIO X

Tempo sugerido: 8 minutos. (Slides de 13 a 17).
Orientação: Peça que os alunos realizem a atividade individualmente.
Propósito: Verificar aprendizagem.
Discuta com a turma:
- Qual a variável dependente na função? E a independente?
RAIO X

Tempo sugerido: 8 minutos. (Slides de 13 a 17).
Orientação: Peça que os alunos realizem a atividade individualmente.
Propósito: Verificar aprendizagem.
Discuta com a turma:
- Qual a variável dependente na função? E a independente?
RAIO X

Tempo sugerido: 8 minutos. (Slides de 13 a 17).
Orientação: Peça que os alunos realizem a atividade individualmente.
Propósito: Verificar aprendizagem.
Discuta com a turma:
- Qual a variável dependente na função? E a independente?
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.