Resumo da aula
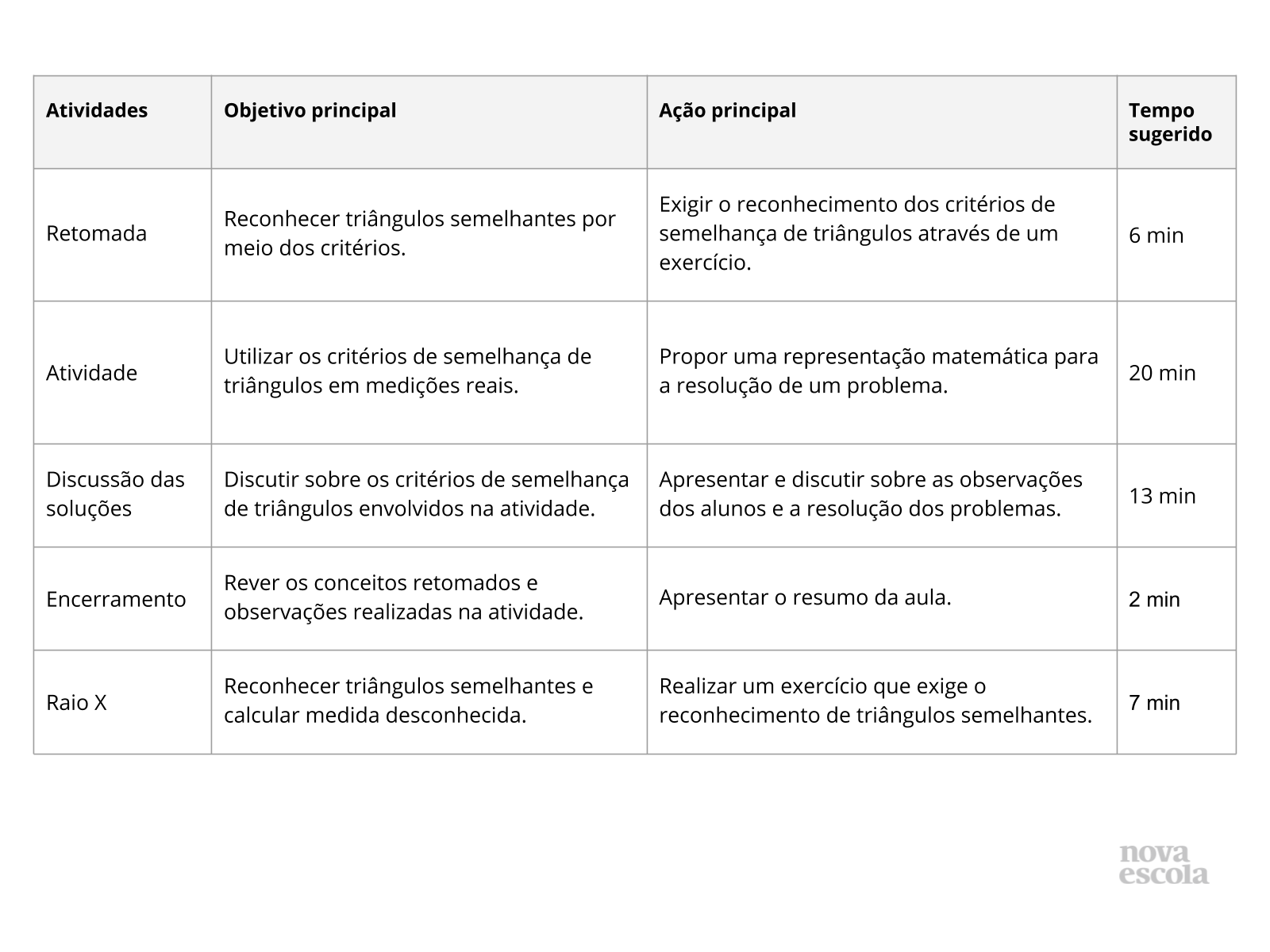
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientações: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada
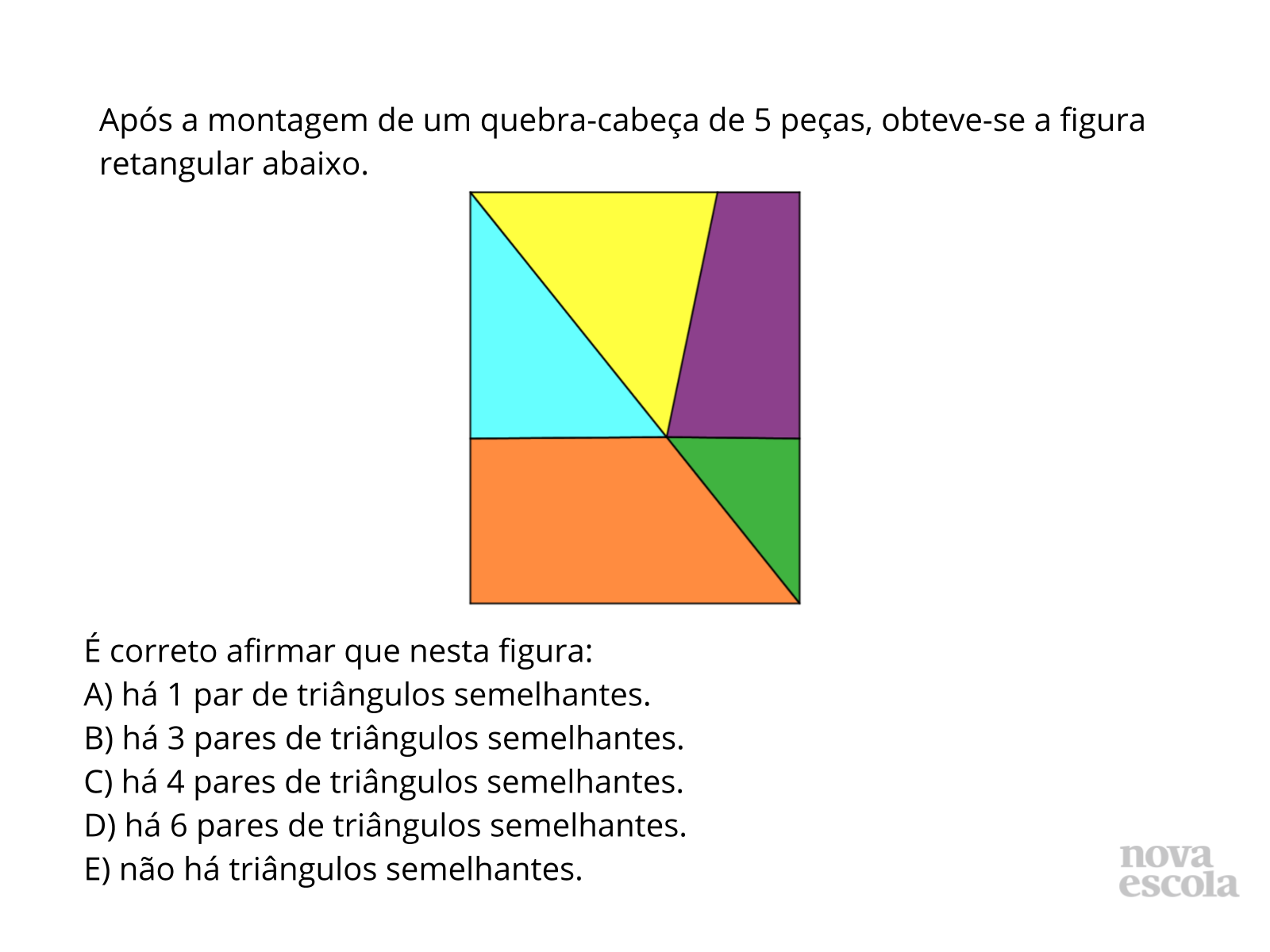
Tempo sugerido: 6 minutos.
Orientações: Deixe que os alunos leiam a atividade e resolvam no caderno.
Propósito: Reconhecer triângulos semelhantes por meio dos critérios.
Discuta com a turma:
- Qual é o único critério de semelhança de triângulos que pode ser utilizado na atividade? Por quê?
- Por que não há triângulo semelhante ao triângulo amarelo?
- Qual é a particularidade dos outros três triângulos que facilitam o reconhecimento da semelhança através do critério AA?
Materiais complementares para impressão:
Aquecimento
Resolução do Aquecimento
Atividade principal

Tempo sugerido: 20 minutos (slides 4 a 8).
Orientações: Peça que, individualmente, os alunos leiam a atividade.
Propósito: Apresentar uma aplicação da semelhança de triângulos e reconhecer a semelhança através dos critérios.
Materiais complementares para impressão:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Atividade principal
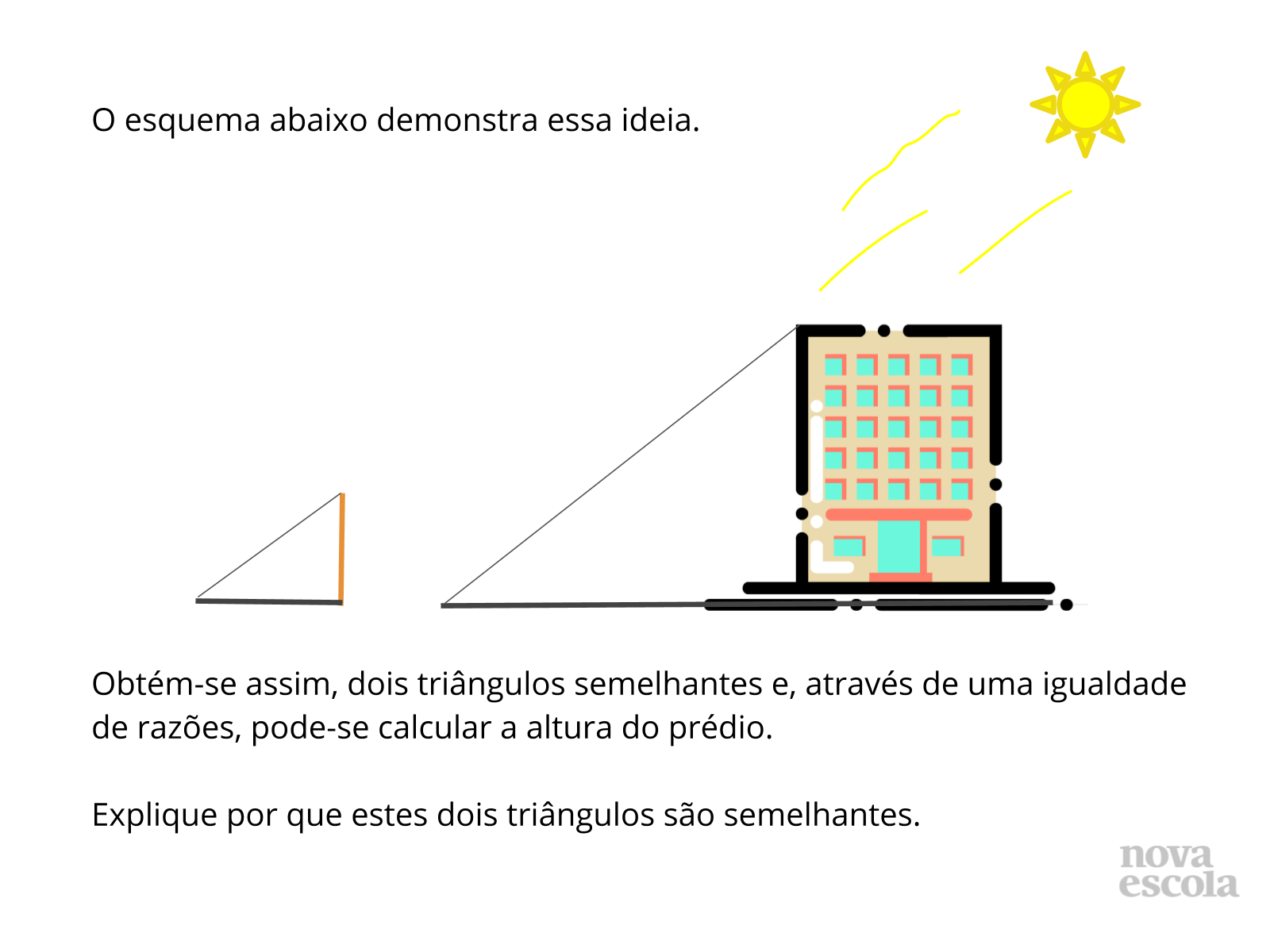
Tempo sugerido: 20 minutos (slides 4 a 8).
Orientações: Peça que, individualmente, os alunos leiam a atividade e façam o que é solicitado.
Propósito: Apresentar uma aplicação da semelhança de triângulos e reconhecer a semelhança através dos critérios.
Discuta com a turma:
- Que informações a situação disponibiliza?
- De que maneira pode-se justificar a semelhança destes triângulos?
Atividade principal
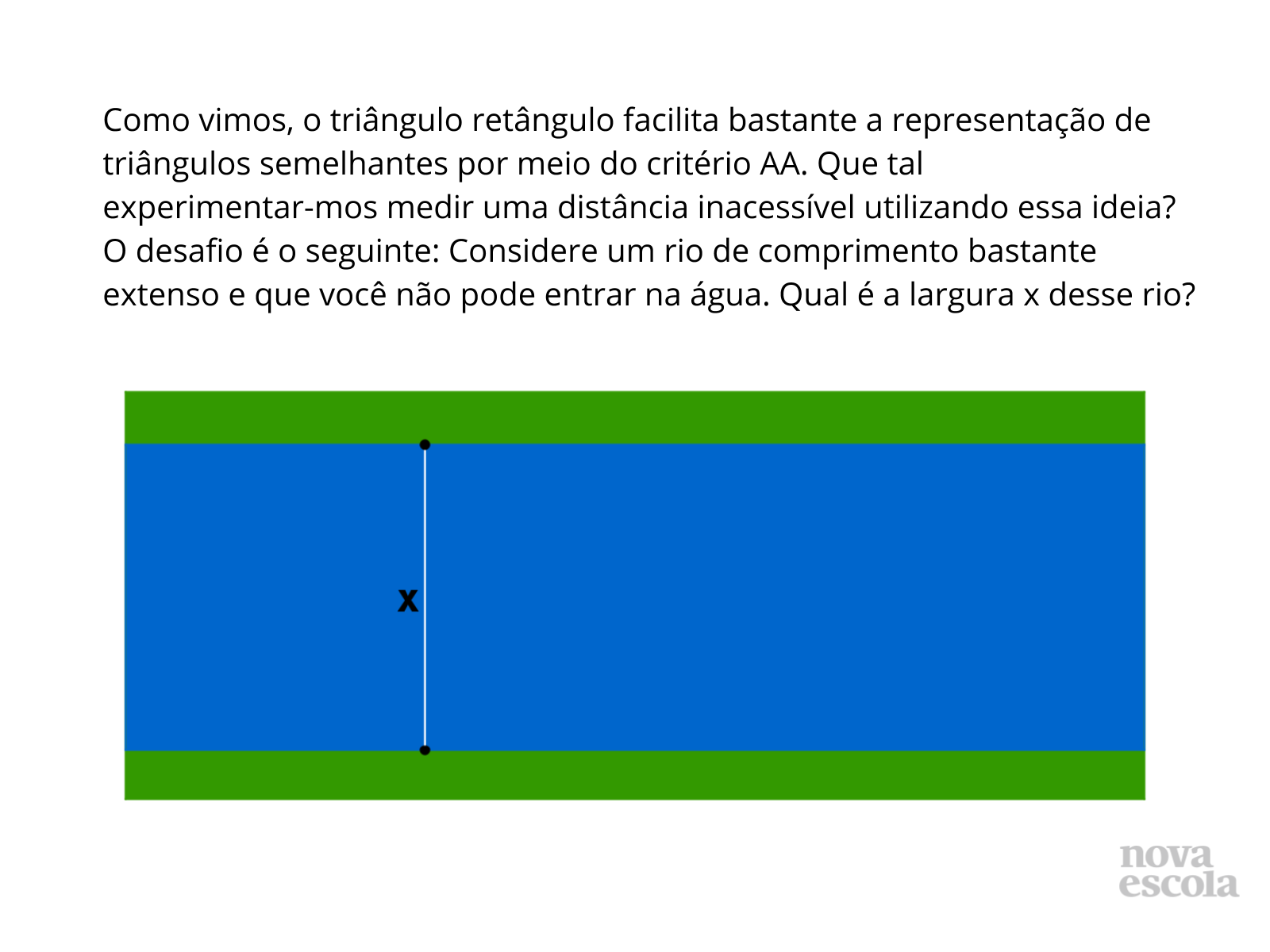
Tempo sugerido: 20 minutos (slides 4 a 8).
Orientações: Peça que, individualmente, os alunos leiam a atividade.
Propósito: Apresentar uma aplicação da semelhança de triângulos e reconhecer a semelhança através dos critérios.
Atividade principal
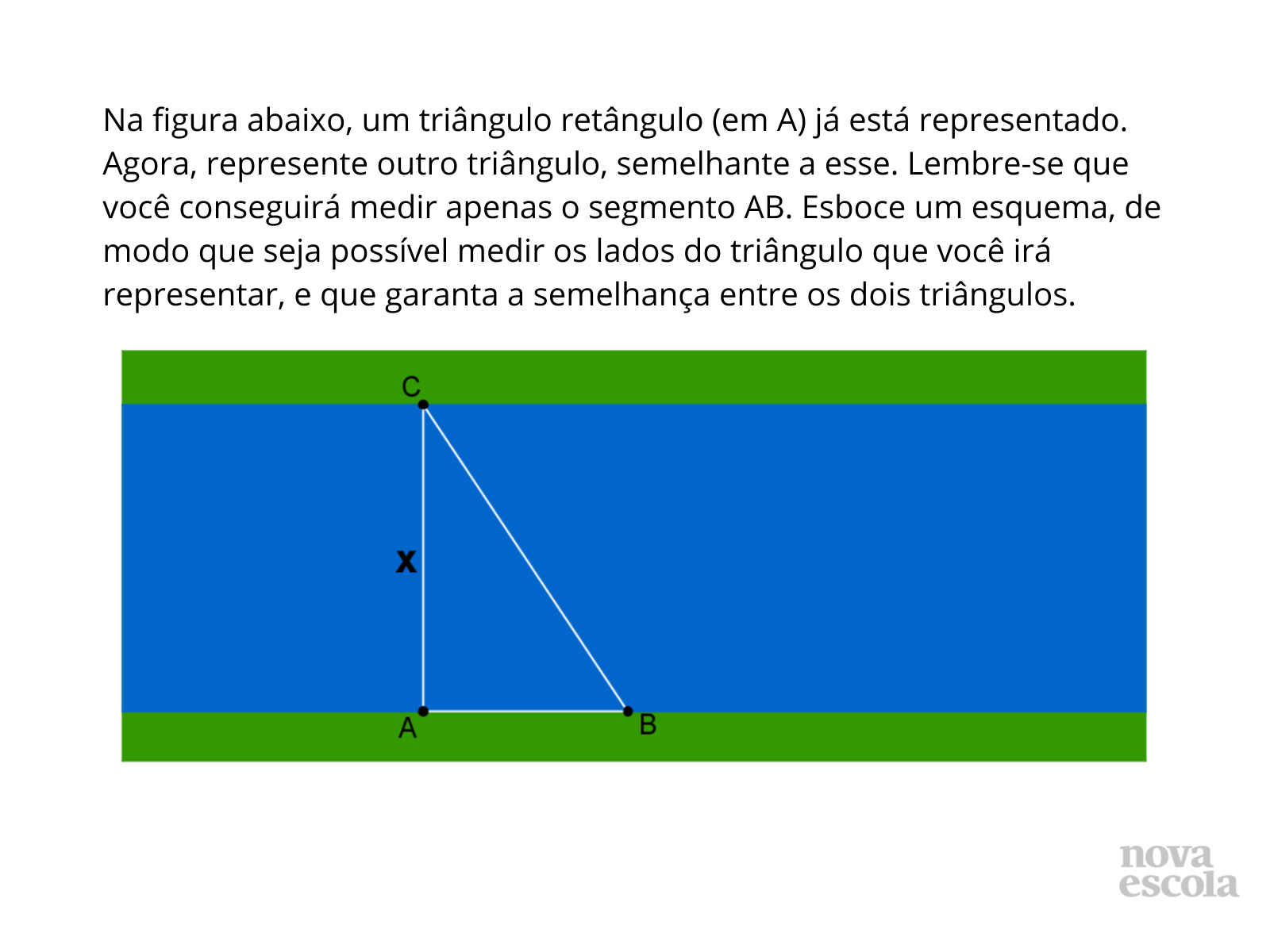
Tempo sugerido: 20 minutos (slides 4 a 8).
Orientações: Organize os alunos em pequenos grupos, de no máximo 5 integrantes. Comente que eles podem imaginar-se na situação para facilitar a proposição de outro triângulo semelhante ao dado.
Propósito: Apresentar uma aplicação da semelhança de triângulos e reconhecer a semelhança através dos critérios.
Discuta com a turma:
- Quando possuímos um par de triângulos semelhantes e se quer obter a medida de um segmento, quantas informações numéricas são necessárias ter?
- De que maneira pode-se representar um triângulo semelhante ao dado na atividade sem saber a medida de seus lados?
Atividade principal

Tempo sugerido: 20 minutos (slides 4 a 8).
Orientações: Encaminhe os alunos até a quadra de esportes. Solicite que levem seus esquemas e lápis para anotar as medidas e leve também uma ou mais fitas métricas por grupo. Cada grupo deverá obter suas medidas, mesmo que o esquema por eles montado seja igual ao de outro grupo. Oriente os alunos que eles próprios podem ser os pontos de referência, para facilitar a visualização de quais distâncias precisarão ser medidas.
Propósito: Apresentar uma aplicação da semelhança de triângulos e reconhecer a semelhança através dos critérios.
Discuta com a turma:
- Em seu esquema, há o prolongamento de algum lado do triângulo retângulo dado? Como podemos garantir que na medição obtenhamos uma linha reta sem “pisar na água”?
- Considerando seu esquema, quantos e quais são os segmentos que precisam ter medida conhecida para obter a largura x do rio?
Discussão de soluções
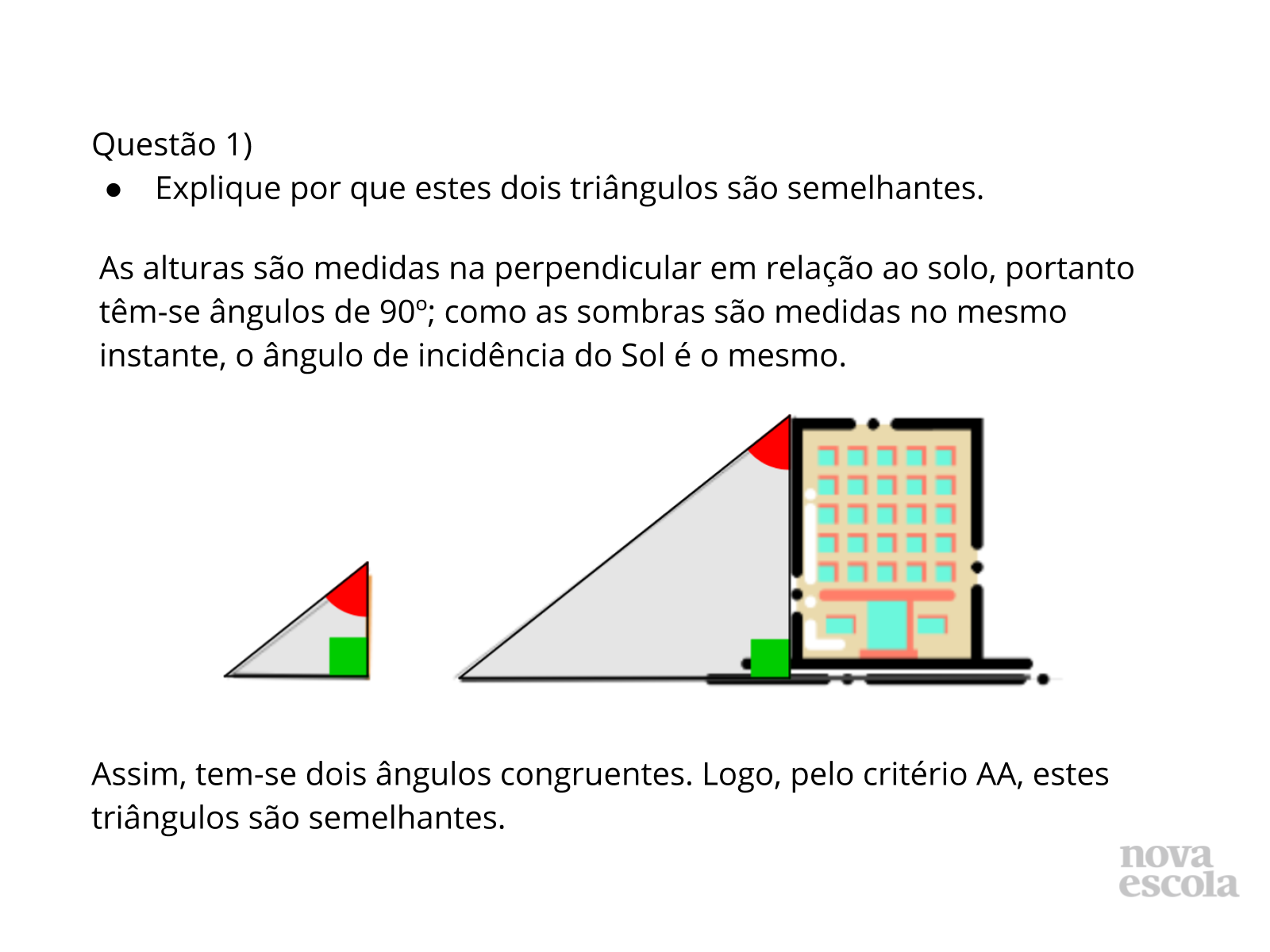
Tempo sugerido: 13 minutos (slides 9, 10 e 11).
Orientações: Convide alguns alunos a expor o que observaram. Neste momento, os alunos deverão refletir sobre suas respostas através de seus questionamentos.
Propósito: Discutir a justificativa dada pelos alunos em relação à semelhança dos triângulos.
Discuta com a turma:
- Através de qual critério podemos afirmar que os triângulos são semelhantes?
- O que garante que há outro par de ângulos congruentes, além do par de ângulos retos?
Discussão de soluções
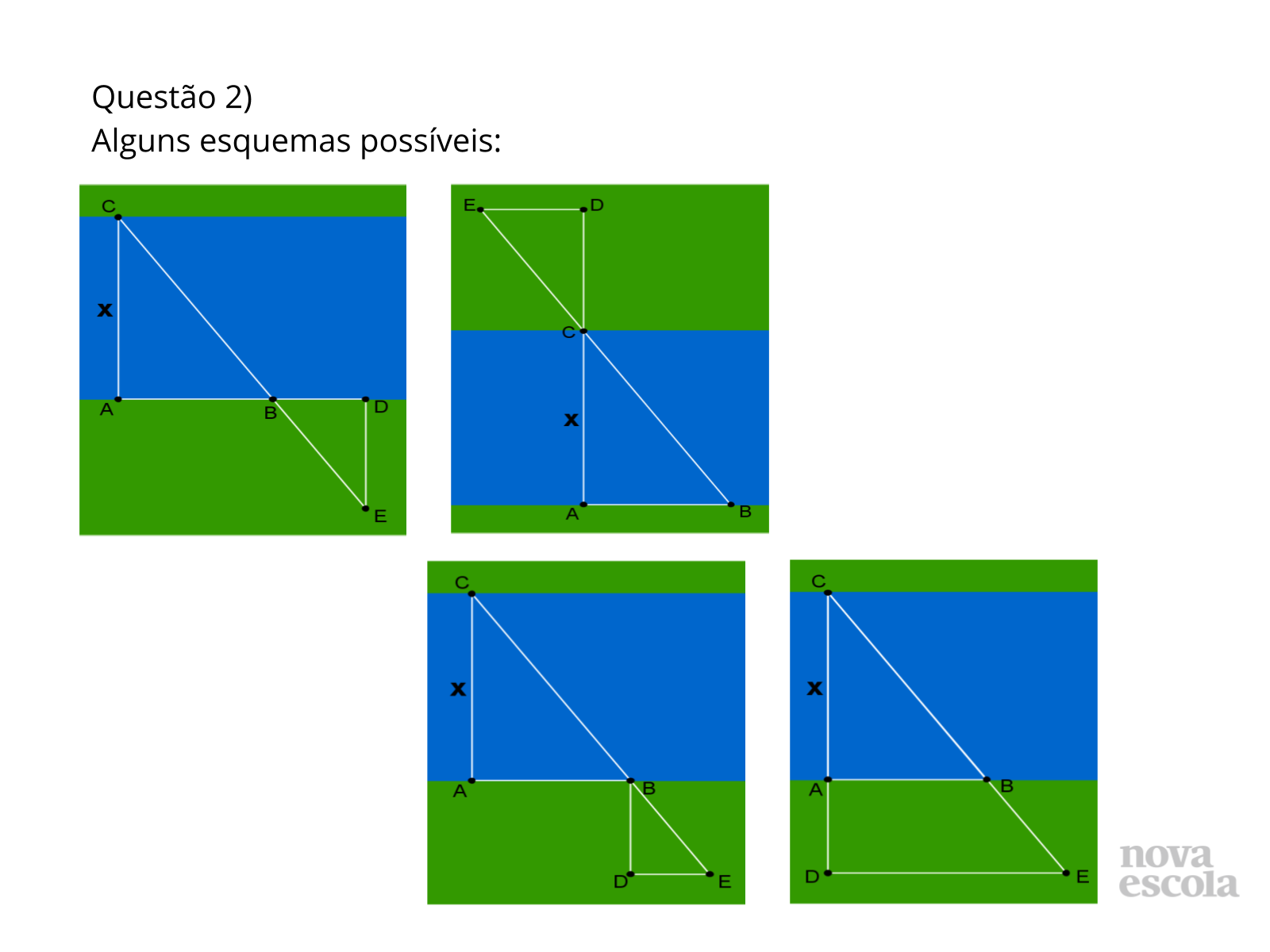
Tempo sugerido: 13 minutos (slides 9, 10 e 11).
Orientações: Convide alguns alunos a expor o esquema que montaram. Você pode também apresentar os esquemas deste slide, se algum não foi apresentado pelos alunos. Solicite que os alunos copiem pelo menos um esquema diferente do seu.
Propósito: Analisar diversos esquemas possíveis para resolver a atividade.
Discuta com a turma:
- Através de qual critério os esquemas foram construídos?
Discussão de soluções
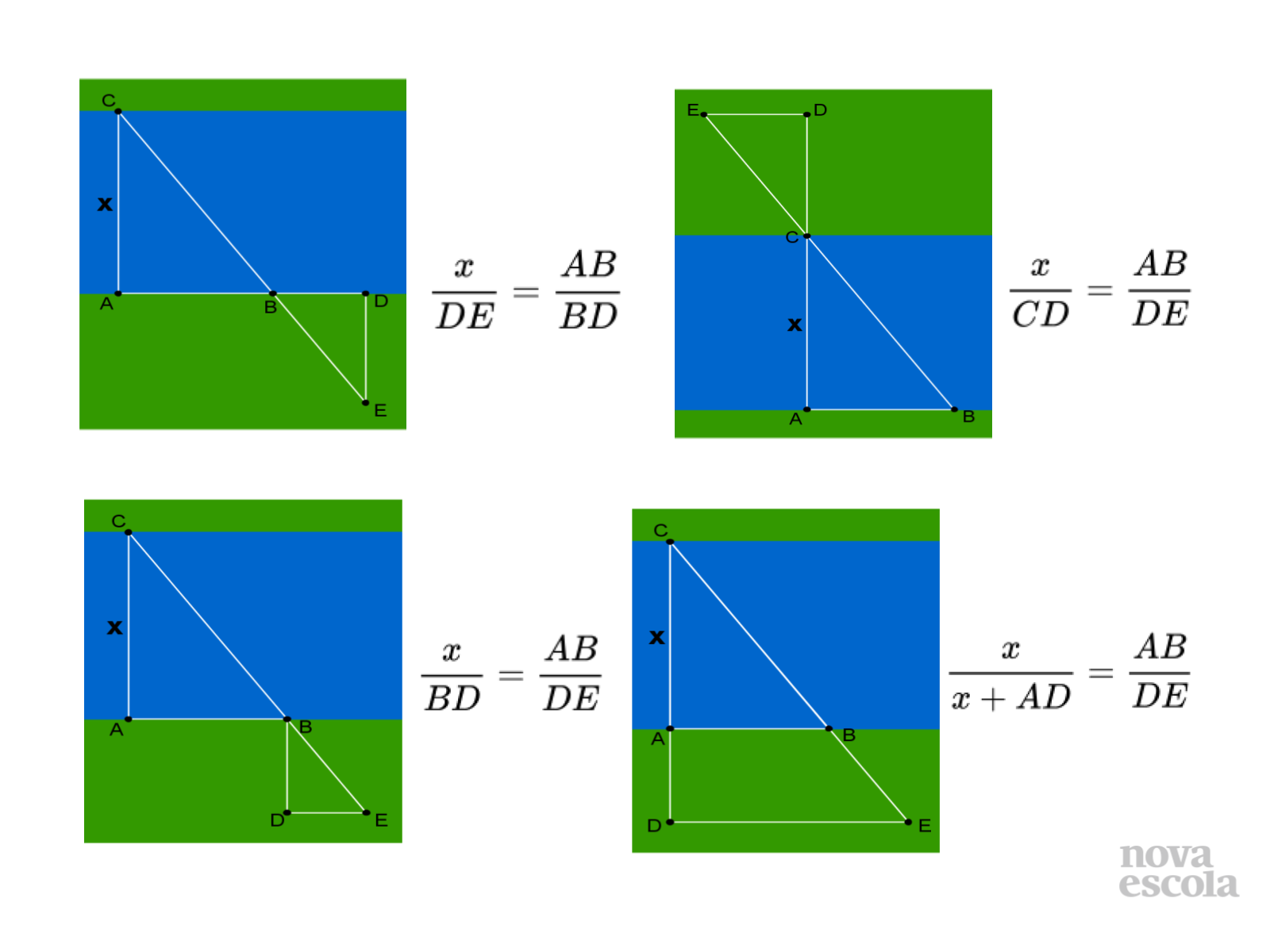
Tempo sugerido: 13 minutos (slides 9, 10 e 11).
Orientações: Convide alguns alunos a expor a proporção montada e a resposta obtida. Você pode também apresentar as proporções deste slide.
Propósito: Analisar as respostas obtidas por meio de cada esquema utilizado.
Discuta com a turma:
- É possível obter uma resposta parecida, através de um mesmo esquema, mas com medidas diferentes? Por que?
Encerramento
Tempo sugerido: 2 minutos.
Orientações: Encerre a atividade retomando com os estudantes as aplicações da semelhança de triângulos vistas na aula. Peça que leiam a conclusão e registrem no caderno a respeito do conceito de semelhança de triângulos e da importância dos critérios de semelhança.
Propósito: Retomar os conceitos envolvidos na atividade principal.
Raio X
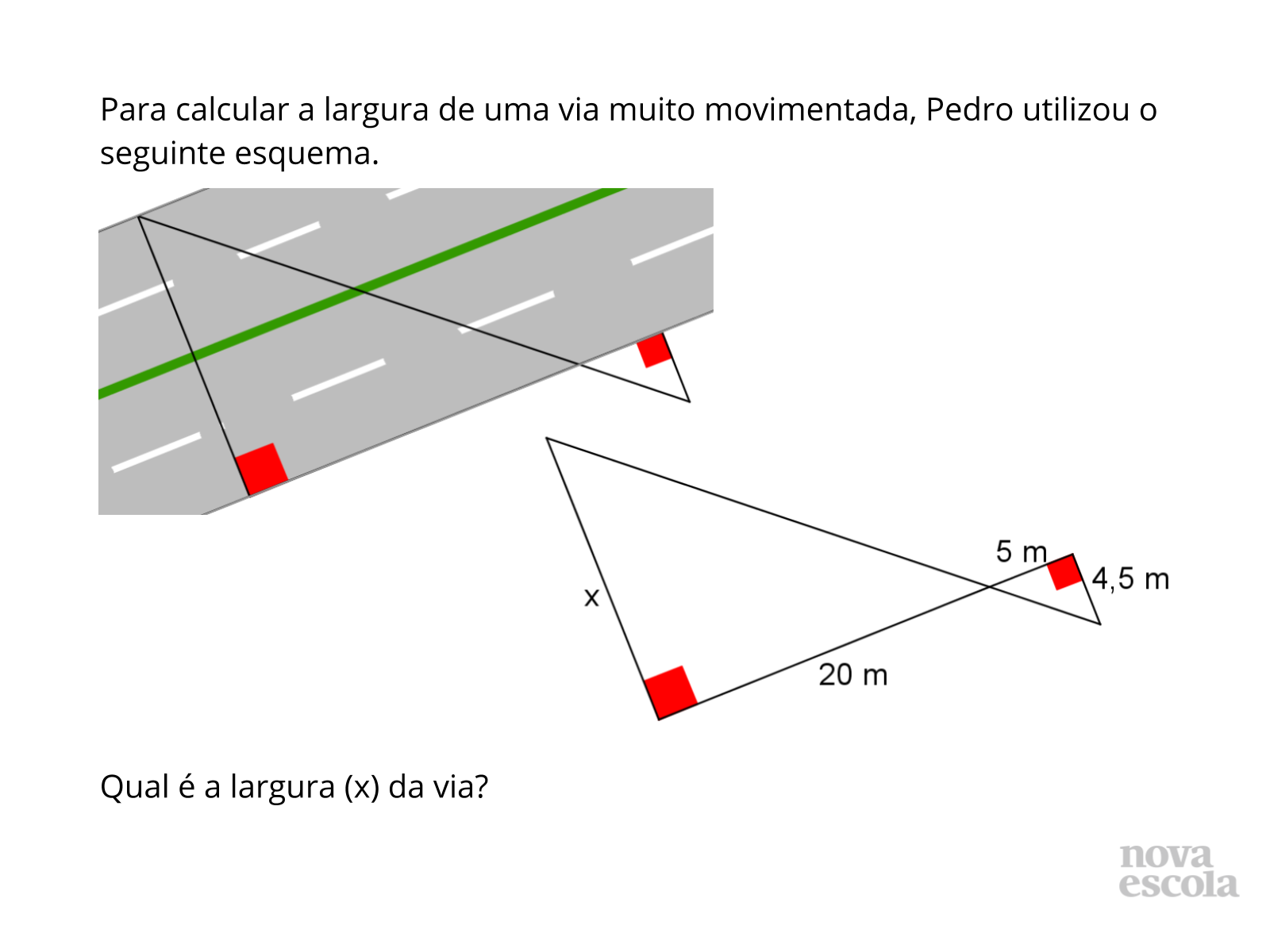
Tempo sugerido: 7 minutos.
Orientações: Peça que, individualmente, os alunos leiam a atividade e a realizem. O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. No final, reserve um tempo para um debate coletivo registrando as soluções na lousa.
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos e montam a proporção corretamente para obter a medida desconhecida.
Discuta com a turma:
- Por que neste tipo de problema podemos afirmar que os dois triângulos obtidos são semelhantes?
- Qual o critério de semelhança de triângulos que sustenta a veracidade desta afirmação?
Materiais complementares para impressão:
Raio X
Resolução do raio x
Atividade complementar
Resolução da atividade complementar