Atividade Principal
Plano de Aula
Plano de aula: Fração como razão entre duas grandezas
Plano 5 de uma sequência de 5 planos. Veja todos os planos sobre As frações em nosso dia a dia
Por: Luiz Filipe Trovão
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Luiz Filipe Trovão
Mentor: Ferdinando Caíque Genghini Dantas Lobo
Especialista: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF07MA06 - Reconhecer que as resoluções de um grupo de problemas que têm a mesma estrutura podem ser obtidas utilizando os mesmo procedimentos.
EF07MA08 - Comparar e ordenar frações associadas às ideias de partes de inteiros, resultado da divisão, razão e operador.
EF07MA09 - Utilizar, na resolução de problemas, a associação entre razão e fração, como a fração 2/3 para expressar a razão de duas partes de uma grandeza para três partes da mesma ou três partes de outra grandeza.
Objetivos específicos
- Realizar uma análise de várias situações problema envolvendo o uso de frações como razão entre duas grandezas.
Conceito-chave
Fração como razão entre duas grandezas, aumentos proporcionais.
Recursos necessários
Lápis, borracha e caderno.
Habilidades BNCC:
Objetivos de aprendizagem
- Realizar uma análise de várias situações problema envolvendo o uso de frações como razão entre duas grandezas.
Resumo da aula
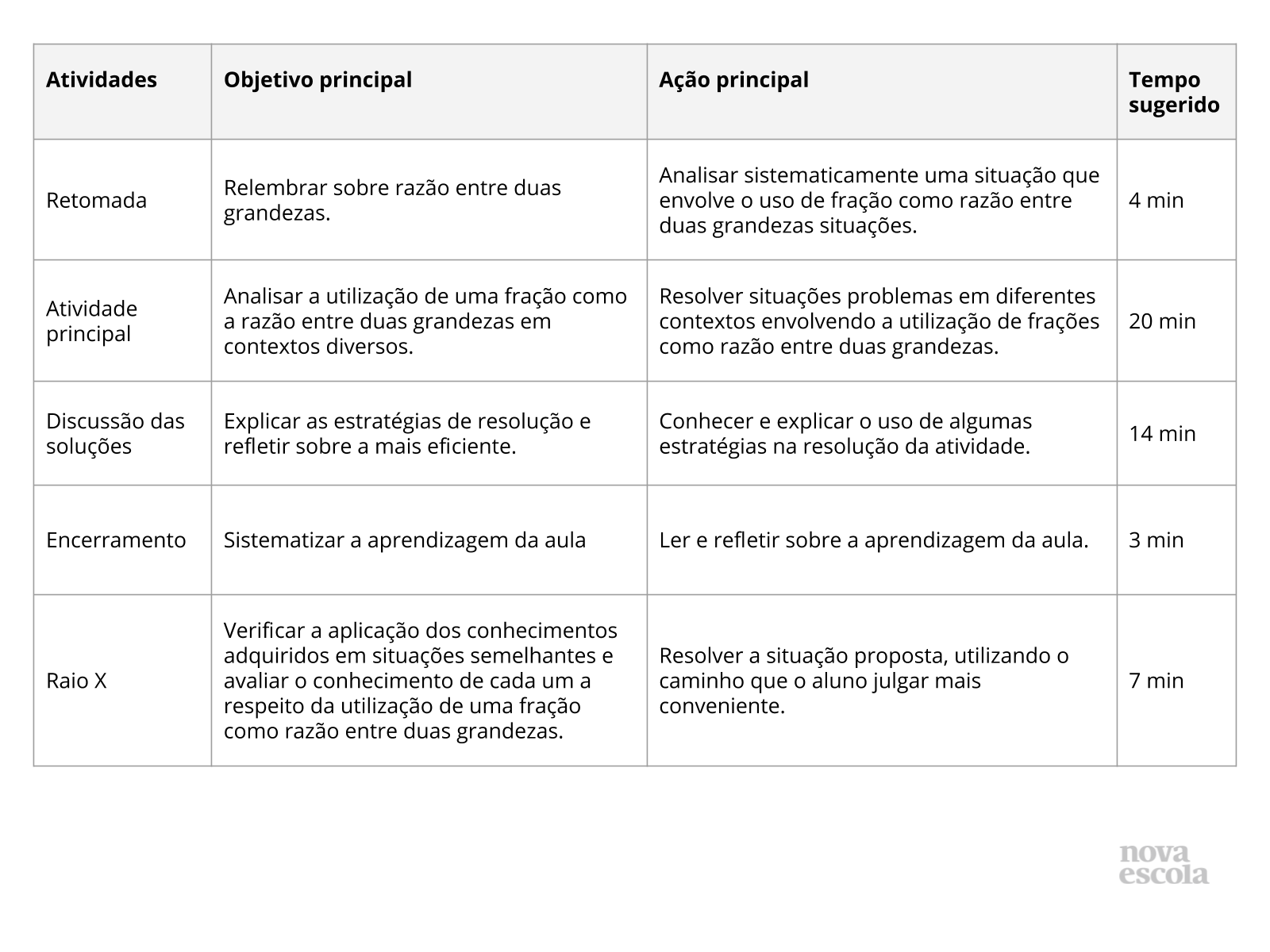
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma. Caso não seja possível a projeção, escreva o objetivo no quadro.
Propósito: Compartilhar o objetivo da aula.
Retomada
Tempo sugerido: 4 minutos
Orientação: Professor, projete o slide para a sala. Caso não seja possível a projeção, leia o texto presente no balão e escreva no quadro ou em um cartaz, a situação presente no restante do slide.
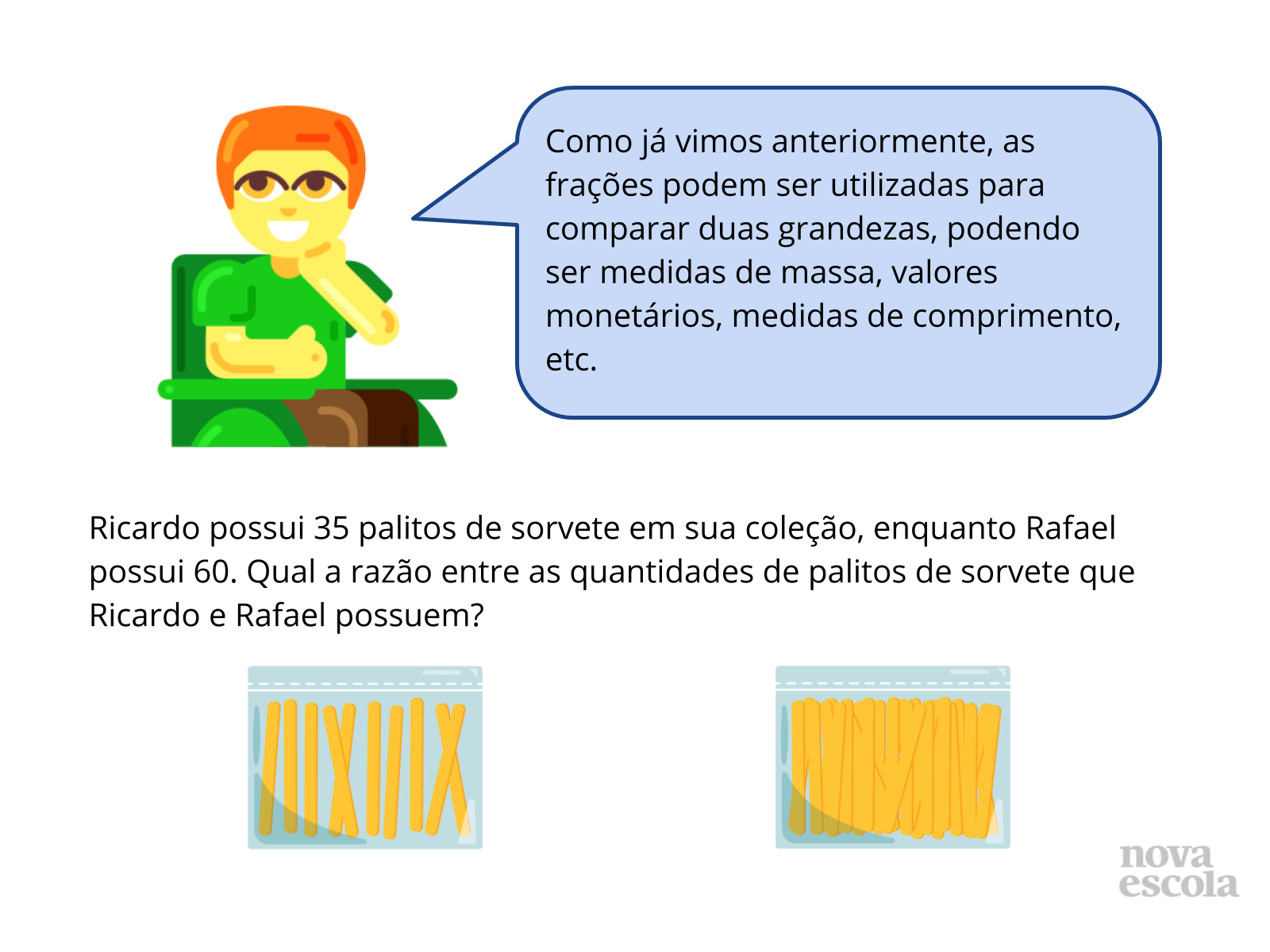
Realize uma reflexão sobre o texto presente no balão de fala, apontando que, como eles já viram anteriormente, as frações também são utilizadas como forma de comparar duas grandezas (ou quaisquer outros tipos de valores). Se necessário, explique para os aluno que grandeza é tudo o que se pode mensurar (medir): distância, massa, altura, valor monetário, entre outros e conclua o balão relembrando aos alunos que essa comparação entre dois valores por meio de uma fração é chamada de razão.
Logo em seguida apresente a situação para os alunos disponibilizando um tempo para que eles resolvam:
“Ricardo possui 35 palitos de sorvete em sua coleção, enquanto Rafael possui 60. Qual a razão entre as quantidades de palitos de sorvete que Ricardo e Rafael possuem?”
Resposta: 35/60 = 7/12? Isso significa que a cada 7 palitos de sorvete que Ricardo possui, Rafael possui 12.
Finalize a retomada apontando que os alunos irão analisar mais algumas situações envolvendo razão.
Propósito: Relembrar o conceito de razão por meio de uma situação cotidiana envolvendo comparação entre grandezas.
Discuta com a turma:
- Qual a diferença em comparar a quantidade de lápis entre Rafael/Ricardo e Ricardo/Rafael?
Atividade Principal

Tempo sugerido: 20 minutos (slides 4 a 6)
Orientação: Imprima ou projete a atividade principal, entregue para os alunos e peça para que eles realizem a leitura das três situações que compõem a atividade. Caso não seja possível a impressão ou projeção, o professor deverá escrever as situações no quadro ou confeccionar um cartaz.
Explique para os alunos que essa atividade será composta inicialmente por três situações, que serão resolvidas e discutidas em trios (para mais informações e possibilidades sobre formações de grupos, consulte as sugestões de leituras e vídeos presentes em Materiais Complementares, ao final dessas anotações).
Professor, discuta com os alunos sobre as possibilidades existentes nas situações, atentando-se as possíveis dúvidas que possam surgir.
Todas as situações têm como intenção, analisar a utilização de frações como razão entre duas grandezas, em diferentes contextos. Por isso, é muito importante que os alunos se atentem à representação de uma razão por meio de uma fração, conforme foi retomado previamente no início da aula.
As três situações apresentam de maneira clara as grandezas que serão comparadas:
Situação 1: nº de caixas de pisos / área de cobertura;
Situação 2: quantidade de abacaxis / valor a pagar;
Situação 3: consumo de litros de combustível / distância percorrida.
O aluno poderá perceber que essa razão entre todos os pares de valores nas situações é o ponto inicial nas suas resoluções, pois é a partir de algumas variações nos valores dessas razões que eles conseguirão encontrar o que se pede nos itens “a” e “b”.
Utilize o guia de intervenções para discutir com os alunos as possibilidades existentes na organização desse problema.
Propósito: Resolver de forma analítica, situações problema variadas, envolvendo o uso de fração como razão entre duas grandezas.
Discuta com a turma:
- Se dobrarmos o número de caixas, o que acontece com a área de cobertura?
- Se triplicarmos o número de abacaxis, o que acontecerá com o valor a ser pago?
- Como comparar dois valores por meio de uma razão? O que a fração 2/3 representa ao ser analisada como uma razão?
Materiais complementares:
Resolução da Atividade Principal
Leituras:
Como agrupo meus alunos: https://novaescola.org.br/conteudo/1475/como-agrupo-meus-alunos
O aprendizado do trabalho em grupo: https://novaescola.org.br/conteudo/605/o-aprendizado-do-trabalho-em-grupo
Vídeo:
Estratégias para formação de grupos: https://novaescola.org.br/conteudo/4063/estrategias-para-formacao-de-grupos
Atividade Principal

Tempo sugerido: 20 minutos (slides 4 a 6)
Orientação: Imprima ou projete a atividade principal, entregue para os alunos e peça para que eles realizem a leitura das três situações que compõem a atividade. Caso não seja possível a impressão ou projeção, o professor deverá escrever as situações no quadro ou confeccionar um cartaz.
Explique para os alunos que essa atividade será composta inicialmente por três situações, que serão resolvidas e discutidas em trios (para mais informações e possibilidades sobre formações de grupos, consulte as sugestões de leituras e vídeos presentes em Materiais Complementares, ao final dessas anotações).
Professor, discuta com os alunos sobre as possibilidades existentes nas situações, atentando-se as possíveis dúvidas que possam surgir.
Todas as situações têm como intenção, analisar a utilização de frações como razão entre duas grandezas, em diferentes contextos. Por isso, é muito importante que os alunos se atentem à representação de uma razão por meio de uma fração, conforme foi retomado previamente no início da aula.
As três situações apresentam de maneira clara as grandezas que serão comparadas:
Situação 1: nº de caixas de pisos / área de cobertura;
Situação 2: quantidade de abacaxis / valor a pagar;
Situação 3: consumo de litros de combustível / distância percorrida.
O aluno poderá perceber que essa razão entre todos os pares de valores nas situações é o ponto inicial nas suas resoluções, pois é a partir de algumas variações nos valores dessas razões que eles conseguirão encontrar o que se pede nos itens “a” e “b”.
Utilize o guia de intervenções para discutir com os alunos as possibilidades existentes na organização desse problema.
Propósito: Resolver de forma analítica, situações problema variadas, envolvendo o uso de fração como razão entre duas grandezas.
Discuta com a turma:
- Se dobrarmos o número de caixas, o que acontece com a área de cobertura?
- Se triplicarmos o número de abacaxis, o que acontecerá com o valor a ser pago?
- Como comparar dois valores por meio de uma razão? O que a fração 2/3 representa ao ser analisada como uma razão?
Materiais complementares:
Resolução da Atividade Principal
Leituras:
Como agrupo meus alunos: https://novaescola.org.br/conteudo/1475/como-agrupo-meus-alunos
O aprendizado do trabalho em grupo: https://novaescola.org.br/conteudo/605/o-aprendizado-do-trabalho-em-grupo
Vídeo:
Estratégias para formação de grupos: https://novaescola.org.br/conteudo/4063/estrategias-para-formacao-de-grupos
Atividade Principal

Tempo sugerido: 20 minutos (slides 4 a 6)
Orientação: Imprima ou projete a atividade principal, entregue para os alunos e peça para que eles realizem a leitura das três situações que compõem a atividade. Caso não seja possível a impressão ou projeção, o professor deverá escrever as situações no quadro ou confeccionar um cartaz.
Explique para os alunos que essa atividade será composta inicialmente por três situações, que serão resolvidas e discutidas em trios (para mais informações e possibilidades sobre formações de grupos, consulte as sugestões de leituras e vídeos presentes em Materiais Complementares, ao final dessas anotações).
Professor, discuta com os alunos sobre as possibilidades existentes nas situações, atentando-se as possíveis dúvidas que possam surgir.
Todas as situações têm como intenção, analisar a utilização de frações como razão entre duas grandezas, em diferentes contextos. Por isso, é muito importante que os alunos se atentem à representação de uma razão por meio de uma fração, conforme foi retomado previamente no início da aula.
As três situações apresentam de maneira clara as grandezas que serão comparadas:
Situação 1: nº de caixas de pisos / área de cobertura;
Situação 2: quantidade de abacaxis / valor a pagar;
Situação 3: consumo de litros de combustível / distância percorrida.
O aluno poderá perceber que essa razão entre todos os pares de valores nas situações é o ponto inicial nas suas resoluções, pois é a partir de algumas variações nos valores dessas razões que eles conseguirão encontrar o que se pede nos itens “a” e “b”.
Utilize o guia de intervenções para discutir com os alunos as possibilidades existentes na organização desse problema.
Propósito: Resolver de forma analítica, situações problema variadas, envolvendo o uso de fração como razão entre duas grandezas.
Discuta com a turma:
- Se dobrarmos o número de caixas, o que acontece com a área de cobertura?
- Se triplicarmos o número de abacaxis, o que acontecerá com o valor a ser pago?
- Como comparar dois valores por meio de uma razão? O que a fração 2/3 representa ao ser analisada como uma razão?
Materiais complementares:
Resolução da Atividade Principal
Leituras:
Como agrupo meus alunos: https://novaescola.org.br/conteudo/1475/como-agrupo-meus-alunos
O aprendizado do trabalho em grupo: https://novaescola.org.br/conteudo/605/o-aprendizado-do-trabalho-em-grupo
Vídeo:
Estratégias para formação de grupos: https://novaescola.org.br/conteudo/4063/estrategias-para-formacao-de-grupos
Discussão da solução

Tempo sugerido: 14 minutos (slides 7 a 13).
Orientação: Inicialmente, peça para que os alunos, ainda em trios, discutam as soluções que obtiveram nas resolução das três situações, sempre acompanhando os grupos em seus raciocínios, pedindo em seguida para que os grupos as exponham para a sala.
Para otimizar esse processo, sugira que cada grupo apresente a solução de um item de cada situação, o 1º grupo apresenta a solução do item “a” da situação 1, o 2º grupo, do item “b” e assim por diante. Quanto mais grupos apresentarem os seus raciocínios mais rica será a discussão.
Após os grupos compartilharem as estratégias utilizadas na resolução das situações, passe para essa série de slides. Caso não seja possível a projeção, o professor deverá reproduzir, pelo menos, os cálculos realizados no quadro ou em um cartaz, o restante da solução pode ser compartilhada de maneira oral para a sala.
As resoluções das três situações, trazem de maneira clara as razões obtidas por meio da comparação entre as grandezas, a serem comparadas inicialmente.
Situação 1: 5/23
Situação 2: 3/13
Situação 3: 2/27
É importante que os alunos percebam que nas três situações as razões entre as grandezas, são a base para o cálculo do valor que está sendo solicitado, pois, é a partir da análise da variação uma grandeza que é possível determinar o comportamento proporcional da outra, como por exemplo na situação “3.a)” sabendo que as grandezas estão na razão 5/23, triplicar um dos valores, implica em triplicar o outro.
Professor, deixe claro para os alunos que a ideia de comparar duas grandezas não implica necessariamente em seu quociente, ou seja, dividir um valor por outro não será útil nesse momento da resolução.
Aponte para eles que as frações foram organizadas de forma que o numerador é o maior valor e o denominador o menor, porém, inverter essa ordem não irá alterar o resultado final.
Professor, a atividade tem como intuito mostrar que a fração como razão entre duas grandezas está presente em diversos contextos e a dinâmica na sua utilização é a mesma independente da situação.
Por isso, após passar por todas as resoluções da atividade, realize a pergunta presente no slide 13: “O que essas situações têm em comum?”. Dê um tempo para os alunos pensarem sobre o questionamento e observe as respostas que eles fornecerem.
Espere como resposta dos alunos: em todas as situações, apontar a razão entre duas grandezas, implica que ao aumentarmos (ou diminuirmos) o valor de uma, estaremos fazendo o mesmo com a outra, na mesma proporção.
Propósito: Apresentar e compartilhar os meios utilizados na obtenção da solução, a fim de expor diferentes caminhos para se obter o mesmo resultado.
Discuta com a turma:
- Nesses contextos, em algum momento, ao aumentarmos um valor estaremos diminuindo o outro? Por quê?
- Ao dobrarmos uma das grandezas, é possível que a outra triplique? Por quê?
Materiais complementares:
Discussão da solução

Tempo sugerido: 14 minutos (slides 7 a 13).
Orientação: Inicialmente, peça para que os alunos, ainda em trios, discutam as soluções que obtiveram nas resolução das três situações, sempre acompanhando os grupos em seus raciocínios, pedindo em seguida para que os grupos as exponham para a sala.
Para otimizar esse processo, sugira que cada grupo apresente a solução de um item de cada situação, o 1º grupo apresenta a solução do item “a” da situação 1, o 2º grupo, do item “b” e assim por diante. Quanto mais grupos apresentarem os seus raciocínios mais rica será a discussão.
Após os grupos compartilharem as estratégias utilizadas na resolução das situações, passe para essa série de slides. Caso não seja possível a projeção, o professor deverá reproduzir, pelo menos, os cálculos realizados no quadro ou em um cartaz, o restante da solução pode ser compartilhada de maneira oral para a sala.
As resoluções das três situações, trazem de maneira clara as razões obtidas por meio da comparação entre as grandezas, a serem comparadas inicialmente.
Situação 1: 5/23
Situação 2: 3/13
Situação 3: 2/27
É importante que os alunos percebam que nas três situações as razões entre as grandezas, são a base para o cálculo do valor que está sendo solicitado, pois, é a partir da análise da variação uma grandeza que é possível determinar o comportamento proporcional da outra, como por exemplo na situação “3.a)” sabendo que as grandezas estão na razão 5/23, triplicar um dos valores, implica em triplicar o outro.
Professor, deixe claro para os alunos que a ideia de comparar duas grandezas não implica necessariamente em seu quociente, ou seja, dividir um valor por outro não será útil nesse momento da resolução.
Aponte para eles que as frações foram organizadas de forma que o numerador é o maior valor e o denominador o menor, porém, inverter essa ordem não irá alterar o resultado final.
Professor, a atividade tem como intuito mostrar que a fração como razão entre duas grandezas está presente em diversos contextos e a dinâmica na sua utilização é a mesma independente da situação.
Por isso, após passar por todas as resoluções da atividade, realize a pergunta presente no slide 13: “O que essas situações têm em comum?”. Dê um tempo para os alunos pensarem sobre o questionamento e observe as respostas que eles fornecerem.
Espere como resposta dos alunos: em todas as situações, apontar a razão entre duas grandezas, implica que ao aumentarmos (ou diminuirmos) o valor de uma, estaremos fazendo o mesmo com a outra, na mesma proporção.
Propósito: Apresentar e compartilhar os meios utilizados na obtenção da solução, a fim de expor diferentes caminhos para se obter o mesmo resultado.
Discuta com a turma:
- Nesses contextos, em algum momento, ao aumentarmos um valor estaremos diminuindo o outro? Por quê?
- Ao dobrarmos uma das grandezas, é possível que a outra triplique? Por quê?
Materiais complementares:
Discussão da solução

Tempo sugerido: 14 minutos (slides 7 a 13).
Orientação: Inicialmente, peça para que os alunos, ainda em trios, discutam as soluções que obtiveram nas resolução das três situações, sempre acompanhando os grupos em seus raciocínios, pedindo em seguida para que os grupos as exponham para a sala.
Para otimizar esse processo, sugira que cada grupo apresente a solução de um item de cada situação, o 1º grupo apresenta a solução do item “a” da situação 1, o 2º grupo, do item “b” e assim por diante. Quanto mais grupos apresentarem os seus raciocínios mais rica será a discussão.
Após os grupos compartilharem as estratégias utilizadas na resolução das situações, passe para essa série de slides. Caso não seja possível a projeção, o professor deverá reproduzir, pelo menos, os cálculos realizados no quadro ou em um cartaz, o restante da solução pode ser compartilhada de maneira oral para a sala.
As resoluções das três situações, trazem de maneira clara as razões obtidas por meio da comparação entre as grandezas, a serem comparadas inicialmente.
Situação 1: 5/23
Situação 2: 3/13
Situação 3: 2/27
É importante que os alunos percebam que nas três situações as razões entre as grandezas, são a base para o cálculo do valor que está sendo solicitado, pois, é a partir da análise da variação uma grandeza que é possível determinar o comportamento proporcional da outra, como por exemplo na situação “3.a)” sabendo que as grandezas estão na razão 5/23, triplicar um dos valores, implica em triplicar o outro.
Professor, deixe claro para os alunos que a ideia de comparar duas grandezas não implica necessariamente em seu quociente, ou seja, dividir um valor por outro não será útil nesse momento da resolução.
Aponte para eles que as frações foram organizadas de forma que o numerador é o maior valor e o denominador o menor, porém, inverter essa ordem não irá alterar o resultado final.
Professor, a atividade tem como intuito mostrar que a fração como razão entre duas grandezas está presente em diversos contextos e a dinâmica na sua utilização é a mesma independente da situação.
Por isso, após passar por todas as resoluções da atividade, realize a pergunta presente no slide 13: “O que essas situações têm em comum?”. Dê um tempo para os alunos pensarem sobre o questionamento e observe as respostas que eles fornecerem.
Espere como resposta dos alunos: em todas as situações, apontar a razão entre duas grandezas, implica que ao aumentarmos (ou diminuirmos) o valor de uma, estaremos fazendo o mesmo com a outra, na mesma proporção.
Propósito: Apresentar e compartilhar os meios utilizados na obtenção da solução, a fim de expor diferentes caminhos para se obter o mesmo resultado.
Discuta com a turma:
- Nesses contextos, em algum momento, ao aumentarmos um valor estaremos diminuindo o outro? Por quê?
- Ao dobrarmos uma das grandezas, é possível que a outra triplique? Por quê?
Materiais complementares:
Discussão da solução

Tempo sugerido: 14 minutos (slides 7 a 13).
Orientação: Inicialmente, peça para que os alunos, ainda em trios, discutam as soluções que obtiveram nas resolução das três situações, sempre acompanhando os grupos em seus raciocínios, pedindo em seguida para que os grupos as exponham para a sala.
Para otimizar esse processo, sugira que cada grupo apresente a solução de um item de cada situação, o 1º grupo apresenta a solução do item “a” da situação 1, o 2º grupo, do item “b” e assim por diante. Quanto mais grupos apresentarem os seus raciocínios mais rica será a discussão.
Após os grupos compartilharem as estratégias utilizadas na resolução das situações, passe para essa série de slides. Caso não seja possível a projeção, o professor deverá reproduzir, pelo menos, os cálculos realizados no quadro ou em um cartaz, o restante da solução pode ser compartilhada de maneira oral para a sala.
As resoluções das três situações, trazem de maneira clara as razões obtidas por meio da comparação entre as grandezas, a serem comparadas inicialmente.
Situação 1: 5/23
Situação 2: 3/13
Situação 3: 2/27
É importante que os alunos percebam que nas três situações as razões entre as grandezas, são a base para o cálculo do valor que está sendo solicitado, pois, é a partir da análise da variação uma grandeza que é possível determinar o comportamento proporcional da outra, como por exemplo na situação “3.a)” sabendo que as grandezas estão na razão 5/23, triplicar um dos valores, implica em triplicar o outro.
Professor, deixe claro para os alunos que a ideia de comparar duas grandezas não implica necessariamente em seu quociente, ou seja, dividir um valor por outro não será útil nesse momento da resolução.
Aponte para eles que as frações foram organizadas de forma que o numerador é o maior valor e o denominador o menor, porém, inverter essa ordem não irá alterar o resultado final.
Professor, a atividade tem como intuito mostrar que a fração como razão entre duas grandezas está presente em diversos contextos e a dinâmica na sua utilização é a mesma independente da situação.
Por isso, após passar por todas as resoluções da atividade, realize a pergunta presente no slide 13: “O que essas situações têm em comum?”. Dê um tempo para os alunos pensarem sobre o questionamento e observe as respostas que eles fornecerem.
Espere como resposta dos alunos: em todas as situações, apontar a razão entre duas grandezas, implica que ao aumentarmos (ou diminuirmos) o valor de uma, estaremos fazendo o mesmo com a outra, na mesma proporção.
Propósito: Apresentar e compartilhar os meios utilizados na obtenção da solução, a fim de expor diferentes caminhos para se obter o mesmo resultado.
Discuta com a turma:
- Nesses contextos, em algum momento, ao aumentarmos um valor estaremos diminuindo o outro? Por quê?
- Ao dobrarmos uma das grandezas, é possível que a outra triplique? Por quê?
Materiais complementares:
Discussão da solução

Tempo sugerido: 14 minutos (slides 7 a 13).
Orientação: Inicialmente, peça para que os alunos, ainda em trios, discutam as soluções que obtiveram nas resolução das três situações, sempre acompanhando os grupos em seus raciocínios, pedindo em seguida para que os grupos as exponham para a sala.
Para otimizar esse processo, sugira que cada grupo apresente a solução de um item de cada situação, o 1º grupo apresenta a solução do item “a” da situação 1, o 2º grupo, do item “b” e assim por diante. Quanto mais grupos apresentarem os seus raciocínios mais rica será a discussão.
Após os grupos compartilharem as estratégias utilizadas na resolução das situações, passe para essa série de slides. Caso não seja possível a projeção, o professor deverá reproduzir, pelo menos, os cálculos realizados no quadro ou em um cartaz, o restante da solução pode ser compartilhada de maneira oral para a sala.
As resoluções das três situações, trazem de maneira clara as razões obtidas por meio da comparação entre as grandezas, a serem comparadas inicialmente.
Situação 1: 5/23
Situação 2: 3/13
Situação 3: 2/27
É importante que os alunos percebam que nas três situações as razões entre as grandezas, são a base para o cálculo do valor que está sendo solicitado, pois, é a partir da análise da variação uma grandeza que é possível determinar o comportamento proporcional da outra, como por exemplo na situação “3.a)” sabendo que as grandezas estão na razão 5/23, triplicar um dos valores, implica em triplicar o outro.
Professor, deixe claro para os alunos que a ideia de comparar duas grandezas não implica necessariamente em seu quociente, ou seja, dividir um valor por outro não será útil nesse momento da resolução.
Aponte para eles que as frações foram organizadas de forma que o numerador é o maior valor e o denominador o menor, porém, inverter essa ordem não irá alterar o resultado final.
Professor, a atividade tem como intuito mostrar que a fração como razão entre duas grandezas está presente em diversos contextos e a dinâmica na sua utilização é a mesma independente da situação.
Por isso, após passar por todas as resoluções da atividade, realize a pergunta presente no slide 13: “O que essas situações têm em comum?”. Dê um tempo para os alunos pensarem sobre o questionamento e observe as respostas que eles fornecerem.
Espere como resposta dos alunos: em todas as situações, apontar a razão entre duas grandezas, implica que ao aumentarmos (ou diminuirmos) o valor de uma, estaremos fazendo o mesmo com a outra, na mesma proporção.
Propósito: Apresentar e compartilhar os meios utilizados na obtenção da solução, a fim de expor diferentes caminhos para se obter o mesmo resultado.
Discuta com a turma:
- Nesses contextos, em algum momento, ao aumentarmos um valor estaremos diminuindo o outro? Por quê?
- Ao dobrarmos uma das grandezas, é possível que a outra triplique? Por quê?
Materiais complementares:
Discussão da solução

Tempo sugerido: 14 minutos (slides 7 a 13).
Orientação: Inicialmente, peça para que os alunos, ainda em trios, discutam as soluções que obtiveram nas resolução das três situações, sempre acompanhando os grupos em seus raciocínios, pedindo em seguida para que os grupos as exponham para a sala.
Para otimizar esse processo, sugira que cada grupo apresente a solução de um item de cada situação, o 1º grupo apresenta a solução do item “a” da situação 1, o 2º grupo, do item “b” e assim por diante. Quanto mais grupos apresentarem os seus raciocínios mais rica será a discussão.
Após os grupos compartilharem as estratégias utilizadas na resolução das situações, passe para essa série de slides. Caso não seja possível a projeção, o professor deverá reproduzir, pelo menos, os cálculos realizados no quadro ou em um cartaz, o restante da solução pode ser compartilhada de maneira oral para a sala.
As resoluções das três situações, trazem de maneira clara as razões obtidas por meio da comparação entre as grandezas, a serem comparadas inicialmente.
Situação 1: 5/23
Situação 2: 3/13
Situação 3: 2/27
É importante que os alunos percebam que nas três situações as razões entre as grandezas, são a base para o cálculo do valor que está sendo solicitado, pois, é a partir da análise da variação uma grandeza que é possível determinar o comportamento proporcional da outra, como por exemplo na situação “3.a)” sabendo que as grandezas estão na razão 5/23, triplicar um dos valores, implica em triplicar o outro.
Professor, deixe claro para os alunos que a ideia de comparar duas grandezas não implica necessariamente em seu quociente, ou seja, dividir um valor por outro não será útil nesse momento da resolução.
Aponte para eles que as frações foram organizadas de forma que o numerador é o maior valor e o denominador o menor, porém, inverter essa ordem não irá alterar o resultado final.
Professor, a atividade tem como intuito mostrar que a fração como razão entre duas grandezas está presente em diversos contextos e a dinâmica na sua utilização é a mesma independente da situação.
Por isso, após passar por todas as resoluções da atividade, realize a pergunta presente no slide 13: “O que essas situações têm em comum?”. Dê um tempo para os alunos pensarem sobre o questionamento e observe as respostas que eles fornecerem.
Espere como resposta dos alunos: em todas as situações, apontar a razão entre duas grandezas, implica que ao aumentarmos (ou diminuirmos) o valor de uma, estaremos fazendo o mesmo com a outra, na mesma proporção.
Propósito: Apresentar e compartilhar os meios utilizados na obtenção da solução, a fim de expor diferentes caminhos para se obter o mesmo resultado.
Discuta com a turma:
- Nesses contextos, em algum momento, ao aumentarmos um valor estaremos diminuindo o outro? Por quê?
- Ao dobrarmos uma das grandezas, é possível que a outra triplique? Por quê?
Materiais complementares:
Discussão da solução

Tempo sugerido: 14 minutos (slides 7 a 13).
Orientação: Inicialmente, peça para que os alunos, ainda em trios, discutam as soluções que obtiveram nas resolução das três situações, sempre acompanhando os grupos em seus raciocínios, pedindo em seguida para que os grupos as exponham para a sala.
Para otimizar esse processo, sugira que cada grupo apresente a solução de um item de cada situação, o 1º grupo apresenta a solução do item “a” da situação 1, o 2º grupo, do item “b” e assim por diante. Quanto mais grupos apresentarem os seus raciocínios mais rica será a discussão.
Após os grupos compartilharem as estratégias utilizadas na resolução das situações, passe para essa série de slides. Caso não seja possível a projeção, o professor deverá reproduzir, pelo menos, os cálculos realizados no quadro ou em um cartaz, o restante da solução pode ser compartilhada de maneira oral para a sala.
As resoluções das três situações, trazem de maneira clara as razões obtidas por meio da comparação entre as grandezas, a serem comparadas inicialmente.
Situação 1: 5/23
Situação 2: 3/13
Situação 3: 2/27
É importante que os alunos percebam que nas três situações as razões entre as grandezas, são a base para o cálculo do valor que está sendo solicitado, pois, é a partir da análise da variação uma grandeza que é possível determinar o comportamento proporcional da outra, como por exemplo na situação “3.a)” sabendo que as grandezas estão na razão 5/23, triplicar um dos valores, implica em triplicar o outro.
Professor, deixe claro para os alunos que a ideia de comparar duas grandezas não implica necessariamente em seu quociente, ou seja, dividir um valor por outro não será útil nesse momento da resolução.
Aponte para eles que as frações foram organizadas de forma que o numerador é o maior valor e o denominador o menor, porém, inverter essa ordem não irá alterar o resultado final.
Professor, a atividade tem como intuito mostrar que a fração como razão entre duas grandezas está presente em diversos contextos e a dinâmica na sua utilização é a mesma independente da situação.
Por isso, após passar por todas as resoluções da atividade, realize a pergunta presente no slide 13: “O que essas situações têm em comum?”. Dê um tempo para os alunos pensarem sobre o questionamento e observe as respostas que eles fornecerem.
Espere como resposta dos alunos: em todas as situações, apontar a razão entre duas grandezas, implica que ao aumentarmos (ou diminuirmos) o valor de uma, estaremos fazendo o mesmo com a outra, na mesma proporção.
Propósito: Apresentar e compartilhar os meios utilizados na obtenção da solução, a fim de expor diferentes caminhos para se obter o mesmo resultado.
Discuta com a turma:
- Nesses contextos, em algum momento, ao aumentarmos um valor estaremos diminuindo o outro? Por quê?
- Ao dobrarmos uma das grandezas, é possível que a outra triplique? Por quê?
Materiais complementares:
Encerramento
Tempo sugerido: 3 minutos
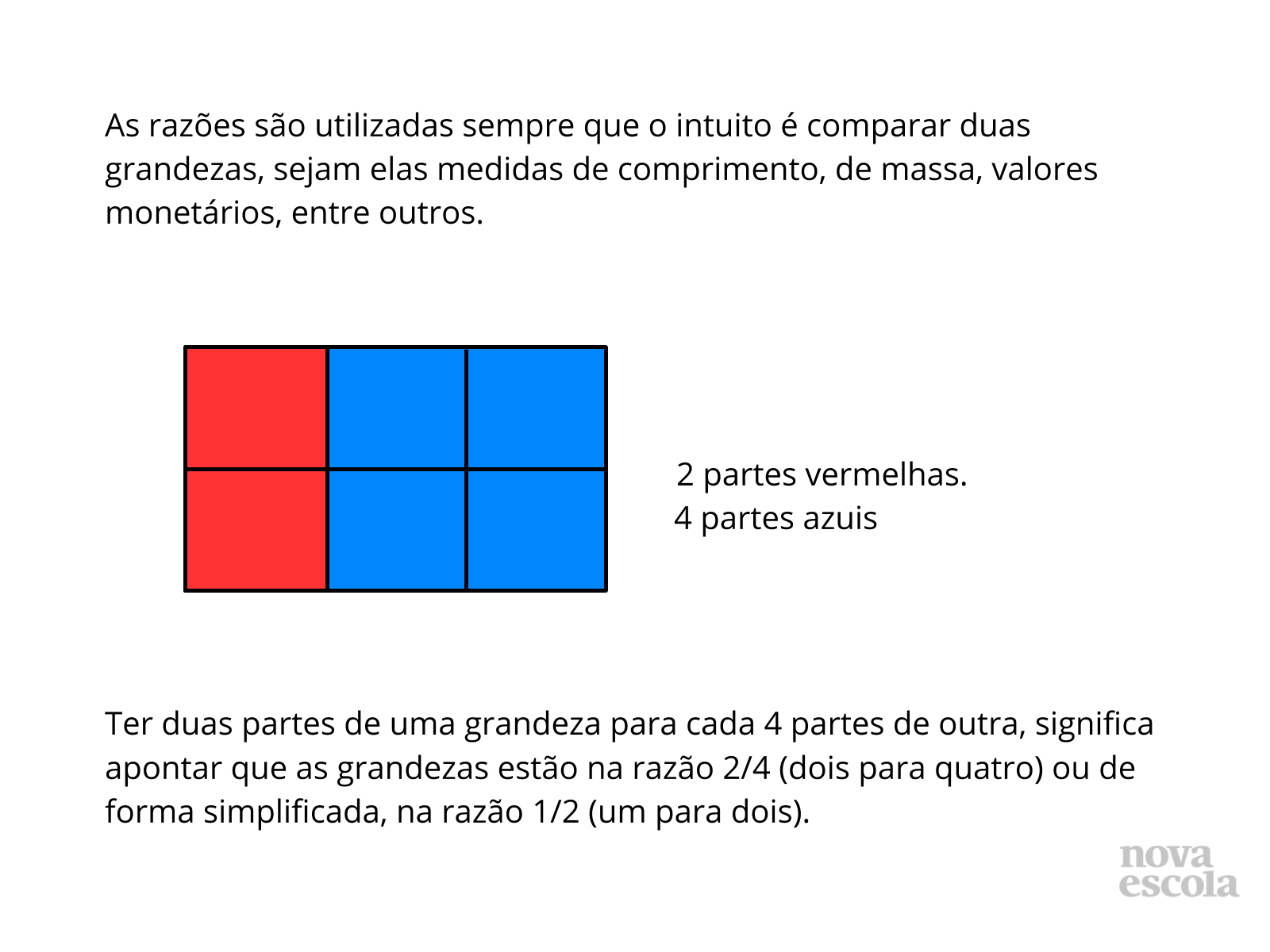
Orientação: Encerre a aula retomando a ideia de razão, apontando alguns exemplos de utilização, reafirmando a todo o momento que a razão é utilizada para comparar grandezas. Finalize apontando a comparação entre os dois valores presentes no slide: quantidade de quadrados vermelhos e quantidade de quadrados azuis, concluindo que as frações são a forma de representar essa comparação.
Propósito: Realizar uma reflexão sobre os conteúdos aprendidos na aula.
Raio X

Tempo sugerido: 7 minutos.
Orientação: Apresente a nova situação e peça para que os alunos analisem e resolvam, em um primeiro momento individualmente e em seguida compartilhando a forma de pensar com o colega ao lado. Você pode projetar, passar no quadro ou fazer o download desta atividade e entregar para os seus alunos. O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure anotar e identificar todos os comentários que surgirem.
Propósito: Realizar uma atividade teórica relativa aos conteúdos ensinados na aula.
Discuta com a turma:
- O que significa dizer que a bebida possui 2 partes de sorvete para 5 partes de chocolate?
- O que significa dizer que a bebida possui 3 partes de sorvete para 4 partes de chocolate?
- É possível afirmar qual lanchonete possui a maior bebida olhando apenas para as partes de sorvete?
- É possível afirmar qual lanchonete possui a maior bebida olhando apenas para as partes de chocolate?
Materiais complementares:
Para os Alunos
Para o Professor
Sugestão de adaptação para ensino remoto
Código do plano
MAT7_06NUM05
Recursos
- Necessários:
- caderno
- lápis
- régua
- grupo de alunos no WhatsApp
- Opcionais:
- Google Sala de Aula
- Meet
- Formulário do Google
Para este plano, foque na etapa: Atividade Principal
Aquecimento
A atividade é uma retomada de conceitos que são fundamentais para a aula. Você pode propor a atividade do slide usando um editor de texto (Google Docs, por exemplo) ou formulário, para que os alunos possam responder à atividade ou, ainda, usar a função de áudio/foto do WhatsApp para que, um a um, postem suas respostas ou hipóteses sobre o assunto disparador. Oriente-os que é um momento de retomada de conteúdos e que caso tenham dúvidas, estas serão trabalhadas no decorrer da aula.
Atividade principal
Para a realização das atividades principais os alunos precisam ter acesso ao problema proposto. Para isso, fotografe a atividade principal e disponibilize a imagem no grupo de WhatsApp para que os alunos possam pensar sobre ele. Oriente-os a filmar ou fotografar as suas estratégias e respostas para compartilhar com o professor e a turma no momento da discussão das soluções.
Discussão das soluções
O intuito desta etapa é deixar claro para os alunos que a ideia de comparar duas grandezas não implica necessariamente em seu quociente, ou seja, dividir um valor por outro. Espere como resposta dos alunos que em todas as situações, apontar a razão entre duas grandezas implica que, ao aumentarmos (ou diminuirmos) o valor de uma, estaremos fazendo proporcionalmente com a outra. Para essas discussões, utilize o meio de comunicação que escolheu na etapa de aquecimento da aula.
Raio X
Proponha a resolução da atividade, enviando-a via WhatsApp, Google Sala de aula ou por meio de um formulário. Peça que compartilhe com o professor a resolução. Analise as resoluções e elabore devolutivas individuais para os alunos.
Convite às famílias
A participação das famílias no processo de aprendizagem é de grande importância para o aluno. Porém, ressaltamos que os pais não são professores de matemática e muitos estão ocupados com outras funções em casa. Portanto, indicamos a participação das famílias no compartilhamento e discussão de possíveis soluções para os problemas propostos.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Luiz Filipe Trovão
Mentor: Ferdinando Caíque Genghini Dantas Lobo
Especialista: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF07MA06 - Reconhecer que as resoluções de um grupo de problemas que têm a mesma estrutura podem ser obtidas utilizando os mesmo procedimentos.
EF07MA08 - Comparar e ordenar frações associadas às ideias de partes de inteiros, resultado da divisão, razão e operador.
EF07MA09 - Utilizar, na resolução de problemas, a associação entre razão e fração, como a fração 2/3 para expressar a razão de duas partes de uma grandeza para três partes da mesma ou três partes de outra grandeza.
Objetivos específicos
- Realizar uma análise de várias situações problema envolvendo o uso de frações como razão entre duas grandezas.
Conceito-chave
Fração como razão entre duas grandezas, aumentos proporcionais.
Recursos necessários
Lápis, borracha e caderno.











