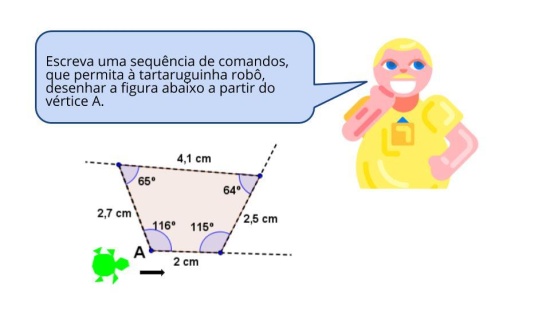
Aquecimento
Plano de Aula
Plano de aula: ngulos em polígonos e a confecção de ferramentas e peças mecânicas
Plano 5 de uma sequência de 5 planos. Veja todos os planos sobre Ângulos em polígonos
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Rosilaine Sanches Martins
Mentor: Fabrício Eduardo Ferreira
Especialista de área: Pricilla Cerqueira
Habilidade da BNCC
(EF07MA22) Calcular medidas de ângulos internos de polígonos regulares, sem o uso de fórmulas, e estabelecer relações entre ângulos internos e externos de polígonos, preferencialmente vinculadas à construção de mosaicos e de ladrilhamentos, à confecção de ferramentas e peças mecânicas, entre outras.
Objetivos específicos
Estabelecer relações entre ângulos internos e externos de polígonos, vinculadas à confecção de ferramentas e peças mecânicas.
Conceito-chave
Ângulos internos de polígonos regulares.
Recursos necessários
- Parafusos e chaves de parafusos de vários tipos;
- Atividades impressas em folhas, coladas no caderno ou não.
Habilidades BNCC:
Objetivos de aprendizagem
Estabelecer relações entre ângulos internos e externos de polígonos, vinculadas à confecção de ferramentas e peças mecânicas.
Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Leia o objetivo da aula para a turma.
Propósito: Apresentar o objetivo da aula para os alunos.
Retomada
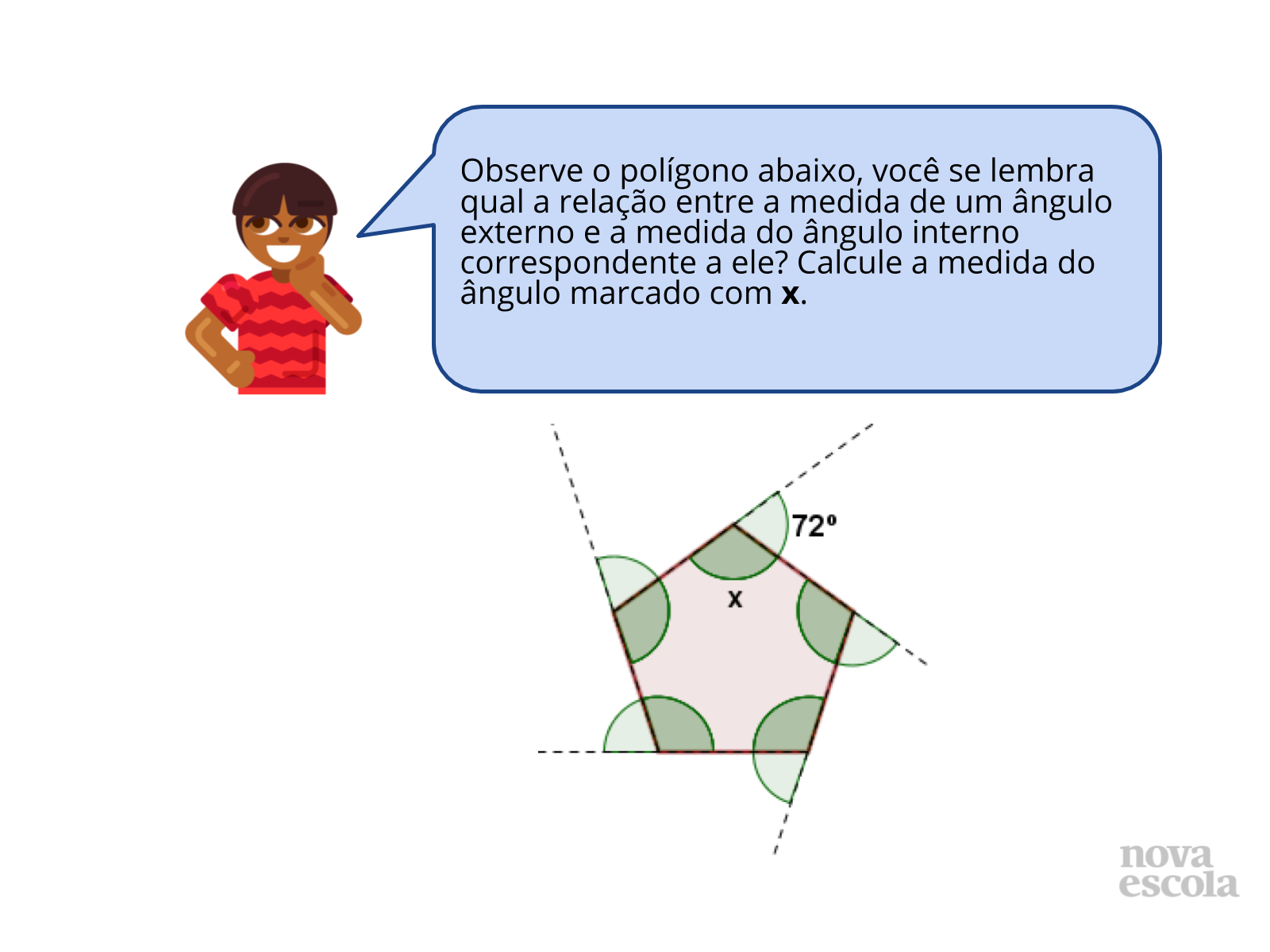
Tempo sugerido: 3 minutos.
Orientação: Apresente o slide para a turma, passe a questão na lousa ou entregue a atividade impressa para cada aluno. Espere que eles a resolvam. Discuta com os alunos as conclusões a que chegaram.
Propósito: Retomar a relação existente entre ângulos externos e internos de polígonos.
Discuta com a turma:
- Conhecendo a medida de um ângulo externo, como poderíamos proceder para descobrir a medida do ângulo interno correspondente a ele?
Materiais complementares para impressão:
Atividade principal
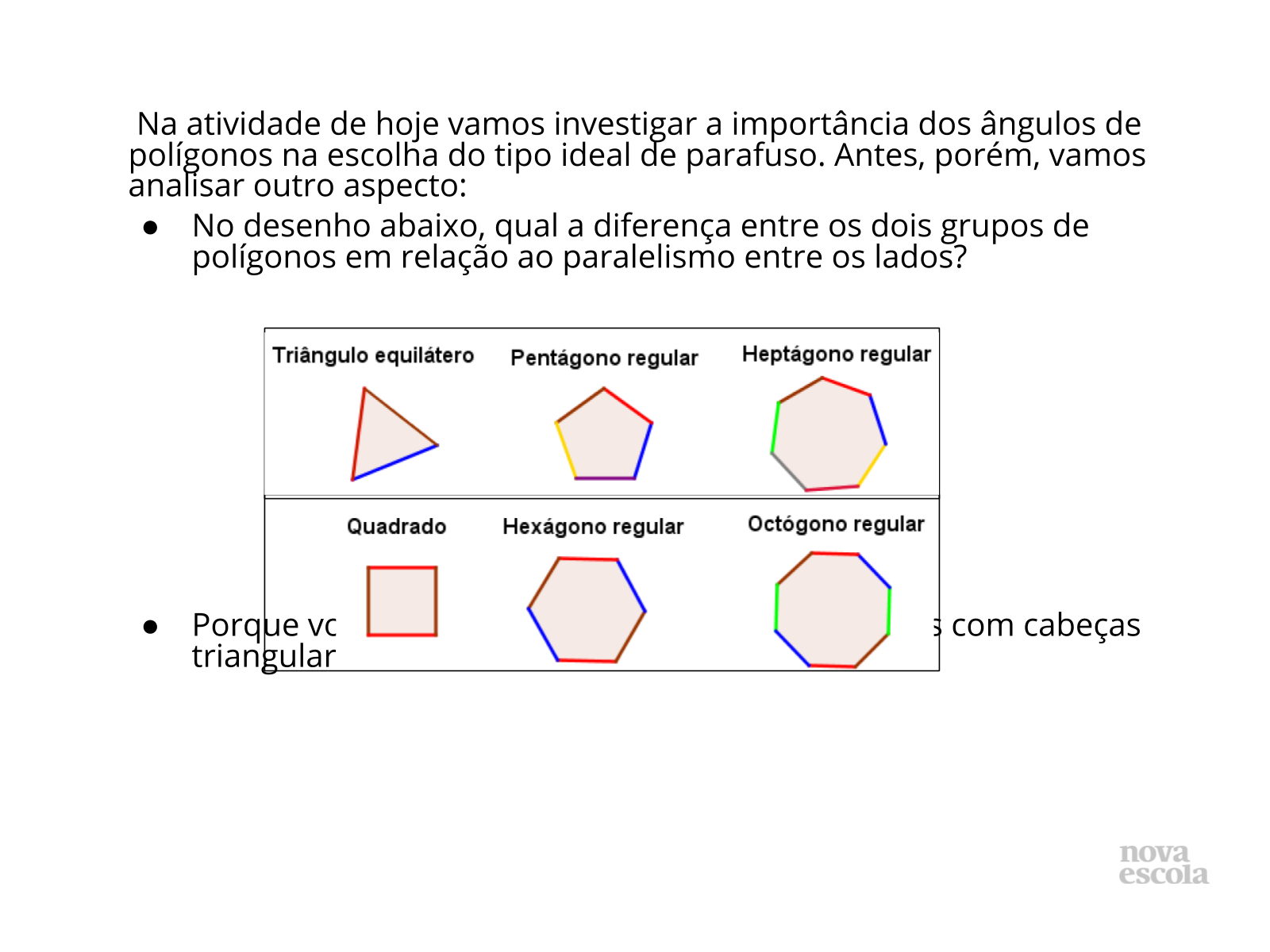
Tempo sugerido: 25 minutos (slides 4, 5, 6 e 7).
Orientação: Leia e discuta o texto do slide 4 com os alunos. Se possível, leve parafusos e chaves para a classe e peça também, em uma aula anterior que os alunos tragam o que encontrarem desse material para a classe. Mostre para os alunos como se encaixa uma chave no parafuso de forma que entendam que o formato da chave é o mesmo da cabeça do parafuso. Em seguida entregue uma folha de atividades para cada aluno, e espere que eles as resolvam. No final de cada atividade, peça aos alunos que compartilhem suas resoluções com a classe.
Propósito: Estudar a medida do ângulo externo e interno de um polígono regular, aplicando estes conceitos no estudo dos diferentes tipos de parafusos e dos aspectos que contribuem para a sua melhor funcionalidade.
Discuta com a turma:
- De que tipo eram os parafusos que já viram?
- Qual o tipo mais comum? Será que existem argumentos matemáticos que justifiquem a utilização deste tipo de parafuso?
- Observando as medidas dos ângulos externos de cada polígono, qual modelo vocês acham que torna o trabalho mais fácil?
- Vocês já ouviram falar em parafuso “espanado”? Vocês sabem porque um parafuso “espana”?
- Qual dos modelos de parafusos apresentados seria melhor para evitar que ele “espane”? Qual seria o pior? Porquê? Como a medida do ângulo do polígono pode interferir nisto?
Materiais complementares para impressão:
Atividade principal
Tempo sugerido: 25 minutos (slides 4, 5, 6 e 7).
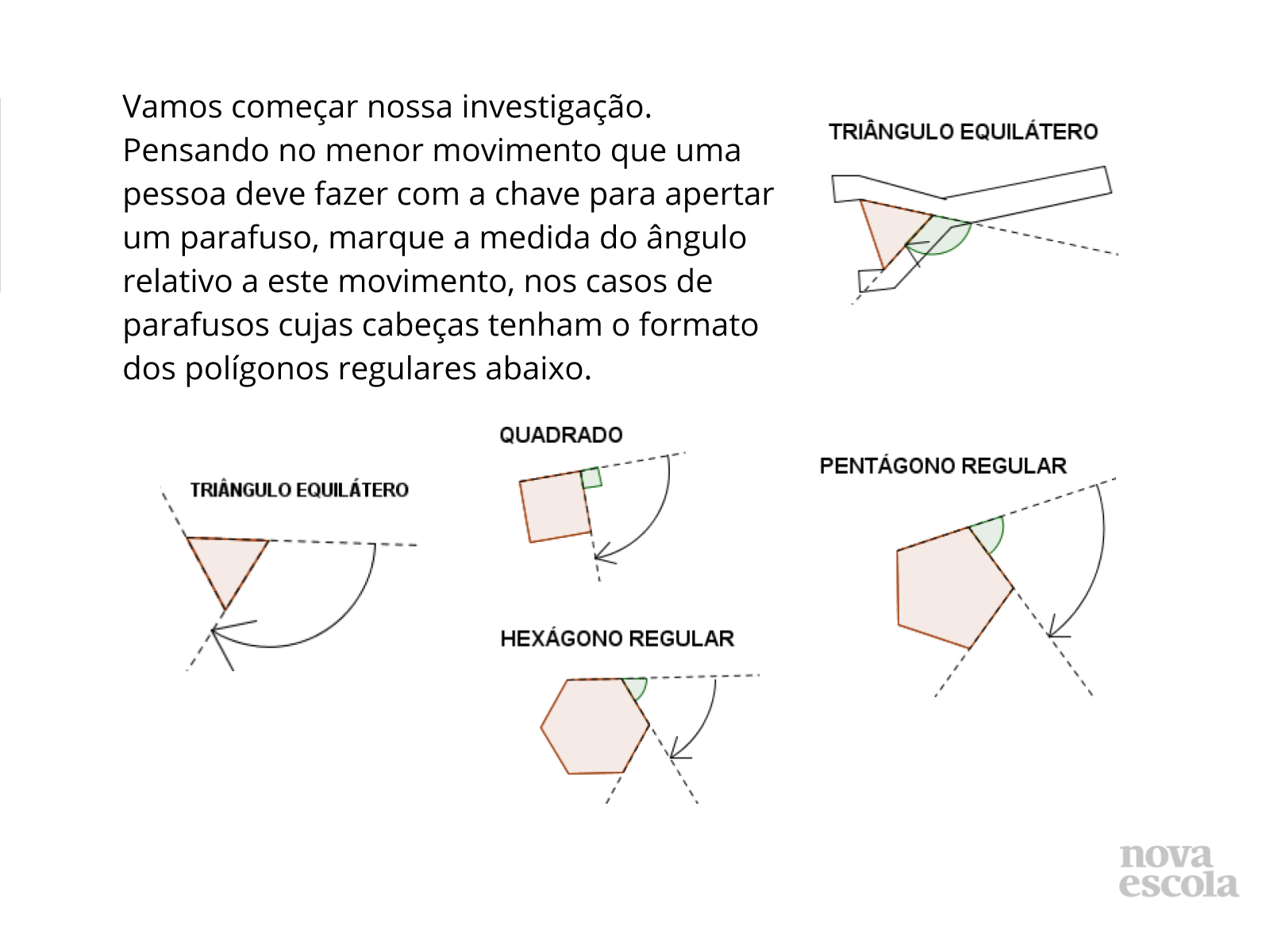
Orientação: Leia e discuta o texto do slide 5 com os alunos. Se possível, leve parafusos e chaves para a classe e peça também, em uma aula anterior que os alunos tragam o que encontrarem desse material para a classe. Mostre para os alunos como se encaixa uma chave no parafuso de forma que entendam que o formato da chave é o mesmo da cabeça do parafuso. Em seguida entregue uma folha de atividades para cada aluno, e espere que eles as resolvam. No final de cada atividade, peça aos alunos que compartilhem suas resoluções com a classe.
Propósito: Estudar a medida do ângulo externo e interno de um polígono regular, aplicando estes conceitos no estudo dos diferentes tipos de parafusos e dos aspectos que contribuem para a sua melhor funcionalidade.
Discuta com a turma:
- De que tipo eram os parafusos que já viram?
- Qual o tipo mais comum? Será que existem argumentos matemáticos que justifiquem a utilização deste tipo de parafuso?
- Observando as medidas dos ângulos externos de cada polígono, qual modelo vocês acham que torna o trabalho mais fácil?
- Vocês já ouviram falar em parafuso “espanado”? Vocês sabem porque um parafuso “espana”?
- Qual dos modelos de parafusos apresentados seria melhor para evitar que ele “espane”? Qual seria o pior? Porquê? Como a medida do ângulo do polígono pode interferir nisto?
Atividade principal
Tempo sugerido: 25 minutos (slides 4, 5, 6 e 7).
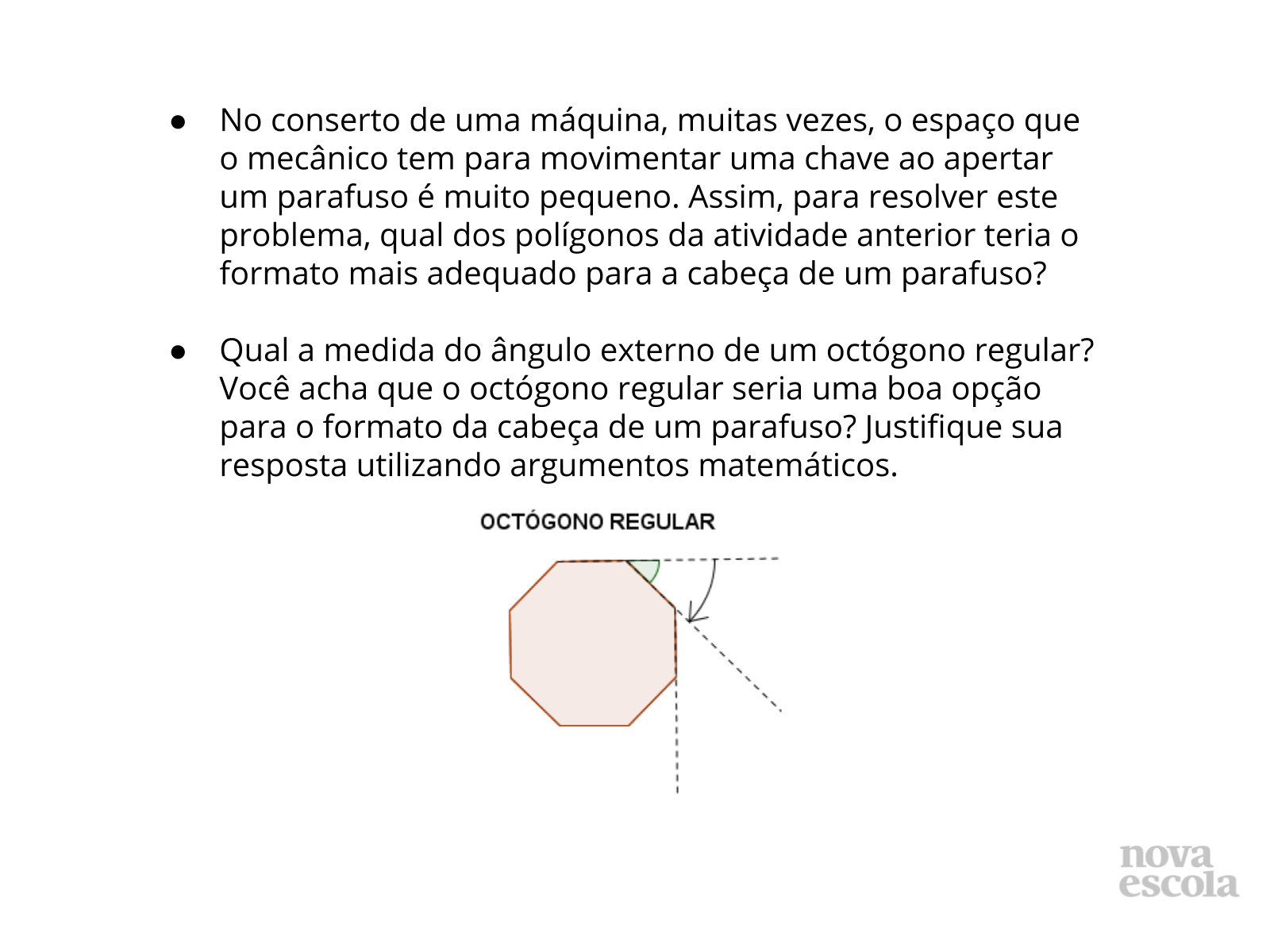
Orientação: Leia e discuta o texto do slide 6 com os alunos. Se possível, leve parafusos e chaves para a classe e peça também, em uma aula anterior que os alunos tragam o que encontrarem desse material para a classe. Mostre para os alunos como se encaixa uma chave no parafuso de forma que entendam que o formato da chave é o mesmo da cabeça do parafuso. Em seguida entregue uma folha de atividades para cada aluno, e espere que eles as resolvam. No final de cada atividade, peça aos alunos que compartilhem suas resoluções com a classe.
Propósito: Estudar a medida do ângulo externo e interno de um polígono regular, aplicando estes conceitos no estudo dos diferentes tipos de parafusos e dos aspectos que contribuem para a sua melhor funcionalidade.
Discuta com a turma:
- De que tipo eram os parafusos que já viram?
- Qual o tipo mais comum? Será que existem argumentos matemáticos que justifiquem a utilização deste tipo de parafuso?
- Observando as medidas dos ângulos externos de cada polígono, qual modelo vocês acham que torna o trabalho mais fácil?
- Vocês já ouviram falar em parafuso “espanado”? Vocês sabem porque um parafuso “espana”?
- Qual dos modelos de parafusos apresentados seria melhor para evitar que ele “espane”? Qual seria o pior? Porquê? Como a medida do ângulo do polígono pode interferir nisto?
Atividade principal
Tempo sugerido: 25 minutos (slides 4, 5, 6 e 7).
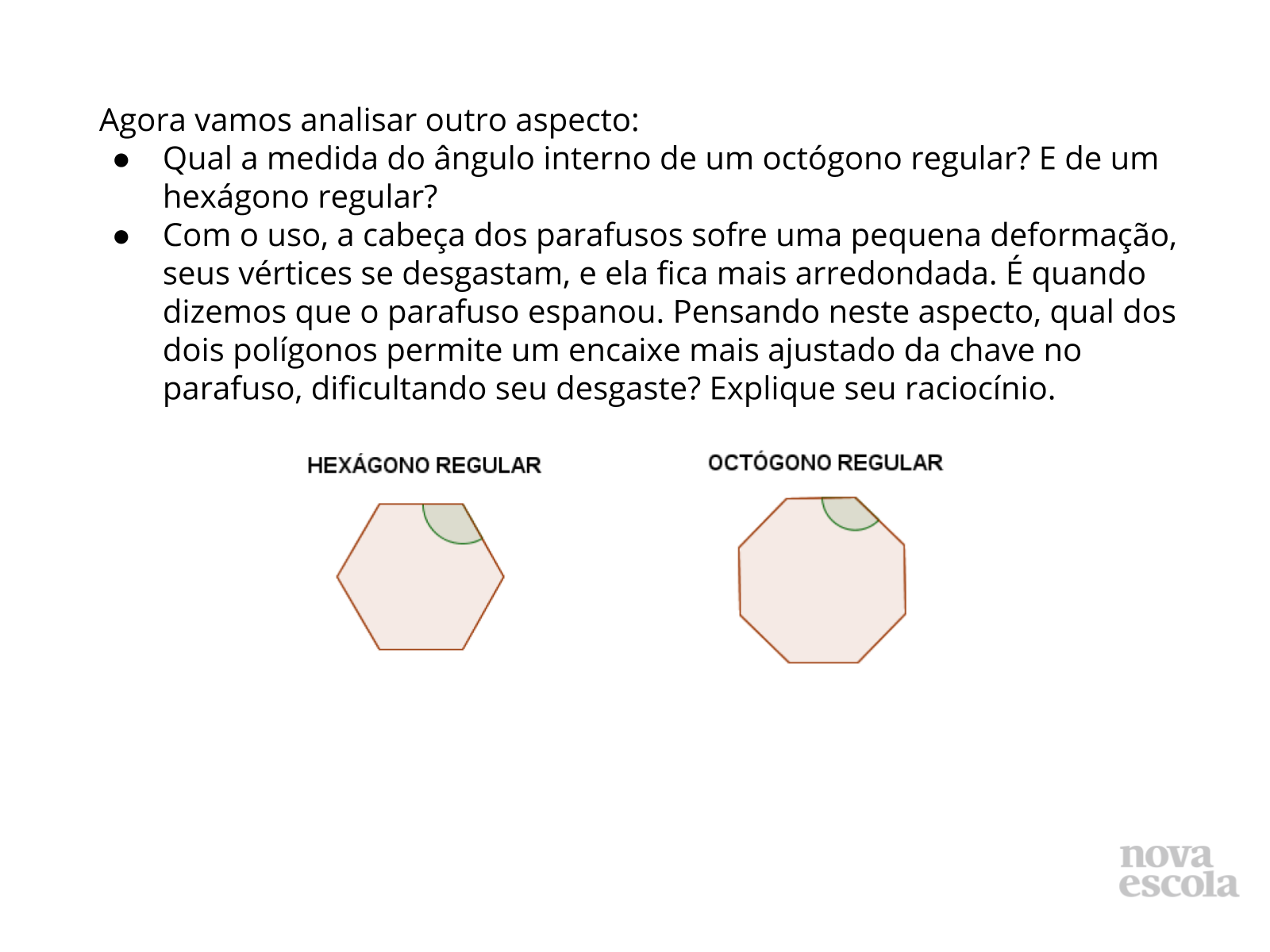
Orientação: Leia e discuta o texto do slide 7 com os alunos. Se possível, leve parafusos e chaves para a classe e peça também, em uma aula anterior que os alunos tragam o que encontrarem desse material para a classe. Mostre para os alunos como se encaixa uma chave no parafuso de forma que entendam que o formato da chave é o mesmo da cabeça do parafuso. Em seguida entregue uma folha de atividades para cada aluno, e espere que eles as resolvam. No final de cada atividade, peça aos alunos que compartilhem suas resoluções com a classe.
Propósito: Estudar a medida do ângulo externo e interno de um polígono regular, aplicando estes conceitos no estudo dos diferentes tipos de parafusos e dos aspectos que contribuem para a sua melhor funcionalidade.
Discuta com a turma:
- De que tipo eram os parafusos que já viram?
- Qual o tipo mais comum? Será que existem argumentos matemáticos que justifiquem a utilização deste tipo de parafuso?
- Observando as medidas dos ângulos externos de cada polígono, qual modelo vocês acham que torna o trabalho mais fácil?
- Vocês já ouviram falar em parafuso “espanado”? Vocês sabem porque um parafuso “espana”?
- Qual dos modelos de parafusos apresentados seria melhor para evitar que ele “espane”? Qual seria o pior? Porquê? Como a medida do ângulo do polígono pode interferir nisto?
Discussão de soluções
Tempo sugerido: 8 minutos (slides 8, 9, 10 e 11).
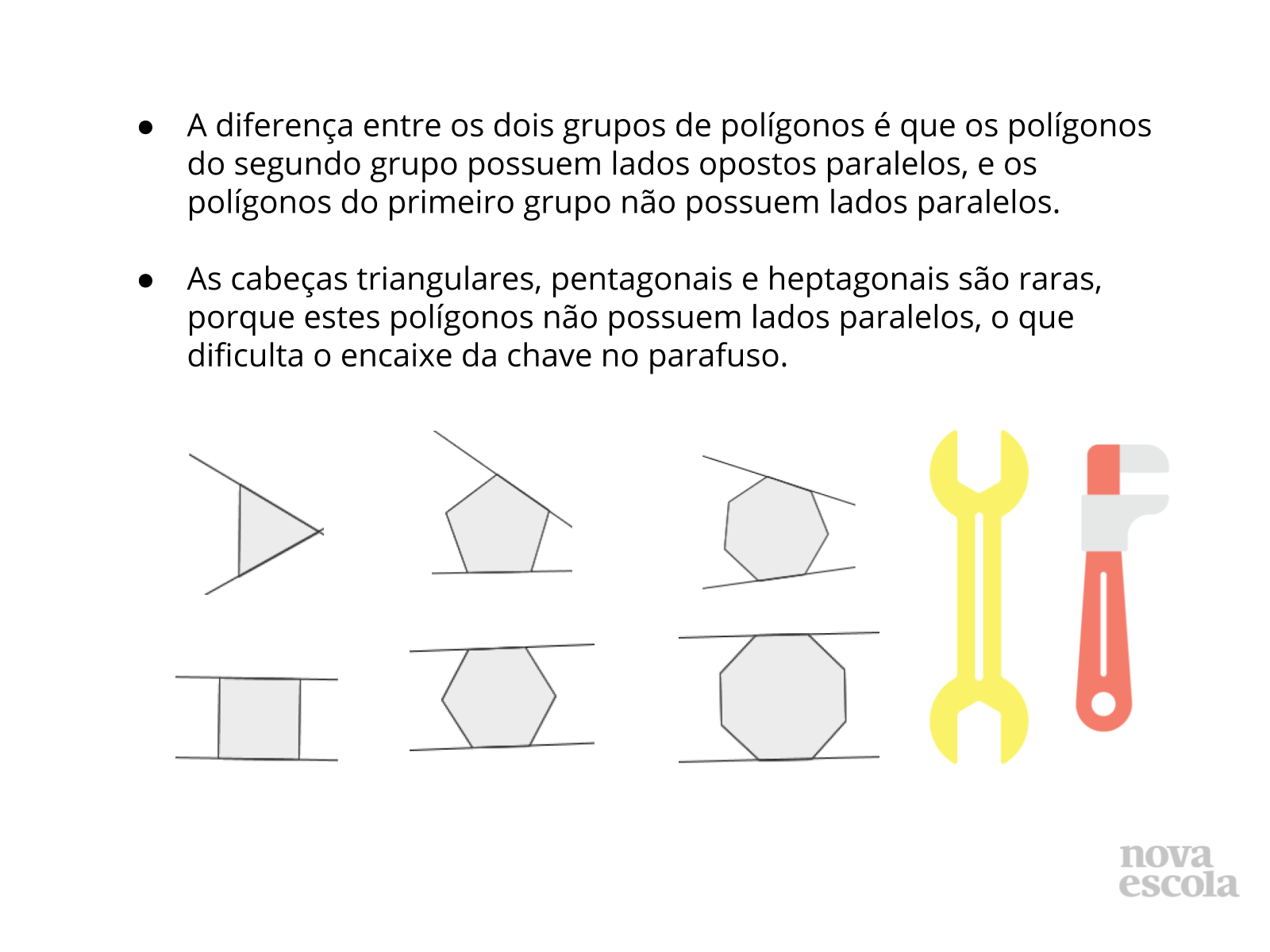
Orientação: Apresente o slide para os alunos ou passe o texto na lousa. Leia e discuta com a turma um ítem de cada vez. Pergunte se algum aluno resolveu de maneira diferente, e peça que exponha seu raciocínio para a classe.
Propósito: Socializar as idéias da turma sobre a relação entre os ângulos externos e internos de polígonos regulares na escolha do tipo ideal de parafusos.
Discuta com a turma:
- Como podemos proceder para calcular a medida do ângulo externo de um polígono regular?
- Vocês já viram um mecânico trabalhar?
- Vocês acham que a medida do ângulo externo interfere na escolha do tipo de parafuso mais adequado para um mecânico, que faz uso dos mesmos em lugares de pouco espaço para movimentos?
- Porque vocês acham que as cabeças dos parafusos espanam? Vocês acham que a medida do ângulo interno interfere neste processo? Como?
Discussão de soluções
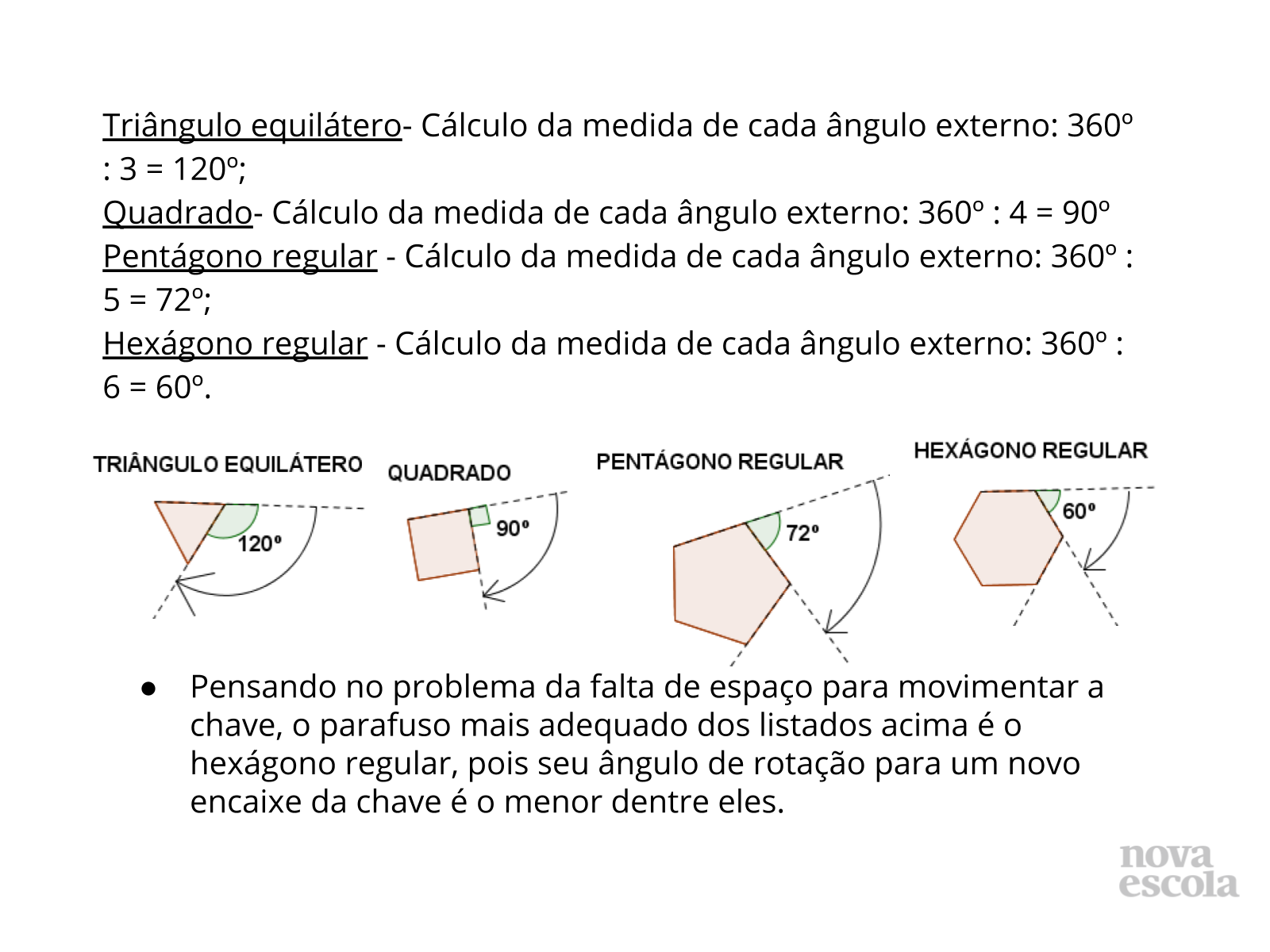
Tempo sugerido: 8 minutos (slides 8, 9, 10 e 11).
Orientação: Apresente o slide para os alunos ou passe o texto na lousa. Leia e discuta com a turma um ítem de cada vez. Pergunte se algum aluno resolveu de maneira diferente, e peça que exponha seu raciocínio para a classe.
Propósito: Socializar as idéias da turma sobre a relação entre os ângulos externos e internos de polígonos regulares na escolha do tipo ideal de parafusos.
Discuta com a turma:
- Como podemos proceder para calcular a medida do ângulo externo de um polígono regular?
- Vocês já viram um mecânico trabalhar?
- Vocês acham que a medida do ângulo externo interfere na escolha do tipo de parafuso mais adequado para um mecânico, que faz uso dos mesmos em lugares de pouco espaço para movimentos?
- Porque vocês acham que as cabeças dos parafusos espanam? Vocês acham que a medida do ângulo interno interfere neste processo? Como?
Discussão de soluções
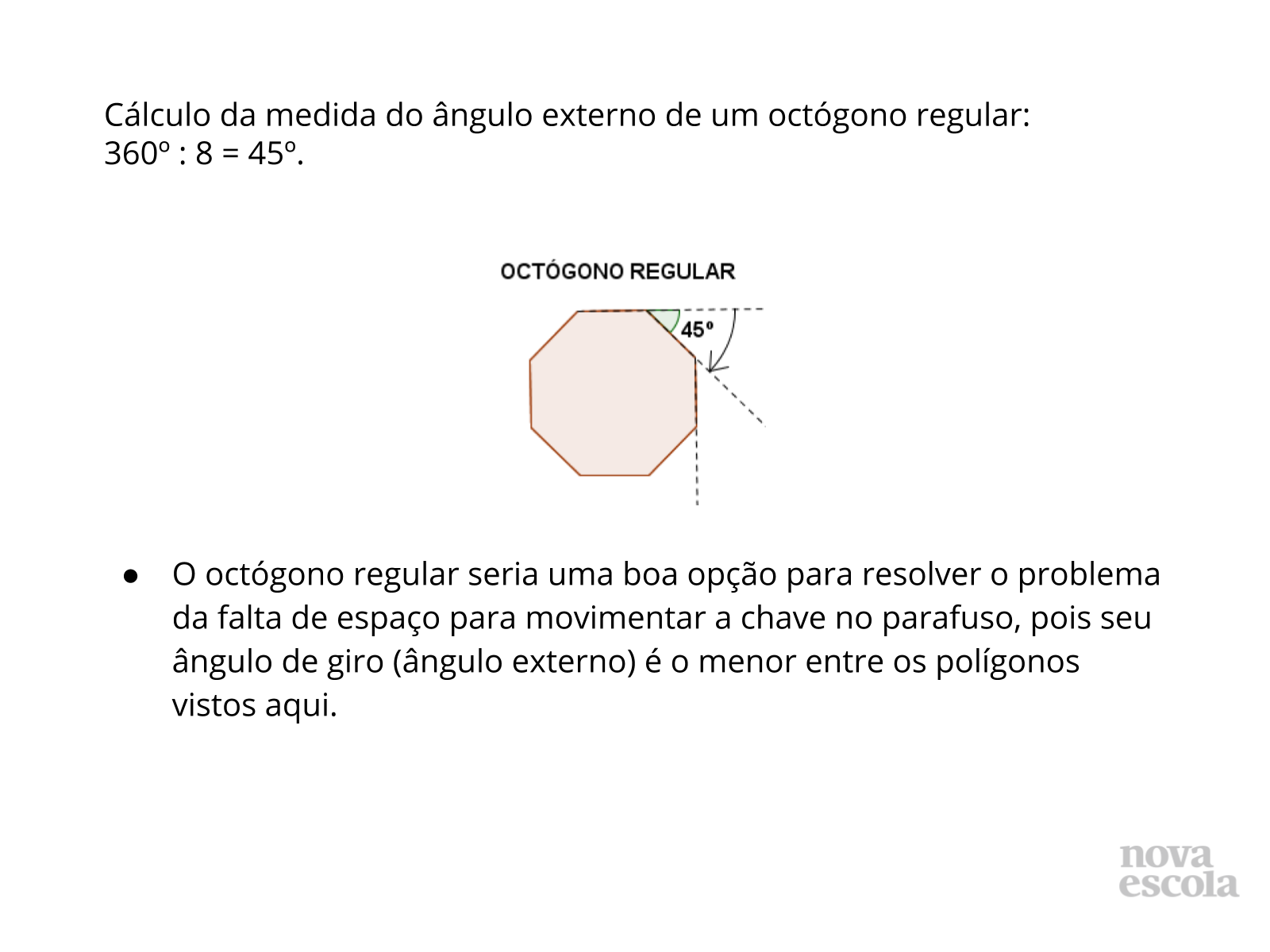
Tempo sugerido: 8 minutos (slides 8, 9, 10 e 11).
Orientação: Apresente o slide para os alunos ou passe o texto na lousa. Leia e discuta com a turma um ítem de cada vez. Pergunte se algum aluno resolveu de maneira diferente, e peça que exponha seu raciocínio para a classe.
Propósito: Socializar as idéias da turma sobre a relação entre os ângulos externos e internos de polígonos regulares na escolha do tipo ideal de parafusos.
Discuta com a turma:
- Como podemos proceder para calcular a medida do ângulo externo de um polígono regular?
- Vocês já viram um mecânico trabalhar?
- Vocês acham que a medida do ângulo externo interfere na escolha do tipo de parafuso mais adequado para um mecânico, que faz uso dos mesmos em lugares de pouco espaço para movimentos?
- Porque vocês acham que as cabeças dos parafusos espanam? Vocês acham que a medida do ângulo interno interfere neste processo? Como?
Discussão de soluções
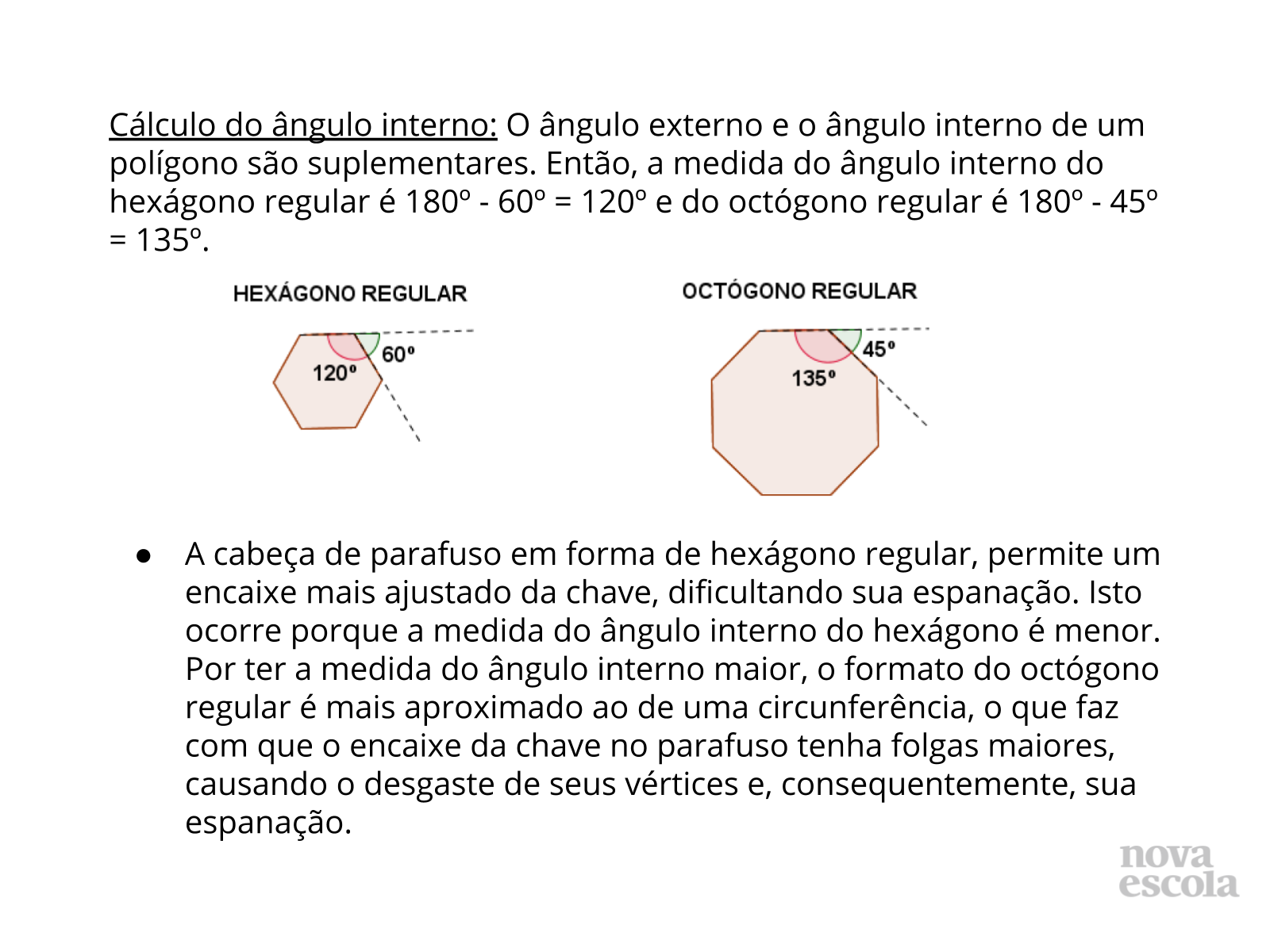
Tempo sugerido: 8 minutos (slides 8, 9, 10 e 11).
Orientação: Apresente o slide para os alunos ou passe o texto na lousa. Leia e discuta com a turma um ítem de cada vez. Pergunte se algum aluno resolveu de maneira diferente, e peça que exponha seu raciocínio para a classe.
Propósito: Socializar as idéias da turma sobre a relação entre os ângulos externos e internos de polígonos regulares na escolha do tipo ideal de parafusos.
Discuta com a turma:
- Como podemos proceder para calcular a medida do ângulo externo de um polígono regular?
- Vocês já viram um mecânico trabalhar?
- Vocês acham que a medida do ângulo externo interfere na escolha do tipo de parafuso mais adequado para um mecânico, que faz uso dos mesmos em lugares de pouco espaço para movimentos?
- Porque vocês acham que as cabeças dos parafusos espanam? Vocês acham que a medida do ângulo interno interfere neste processo? Como?
Encerramento

Tempo sugerido: 5 minutos.
Orientação: Leia e discuta com a turma o texto do slide.
Propósito: Generalizar os aspectos estudados na aula sobre a confecção de parafusos com cabeças poligonais e sua relação com os ângulos dos polígonos.
Discuta com a turma:
- Você concorda que o parafuso com cabeça em forma de hexágono regular é o que mais atende aos quesitos estudados? Justifique sua resposta.
Raio X
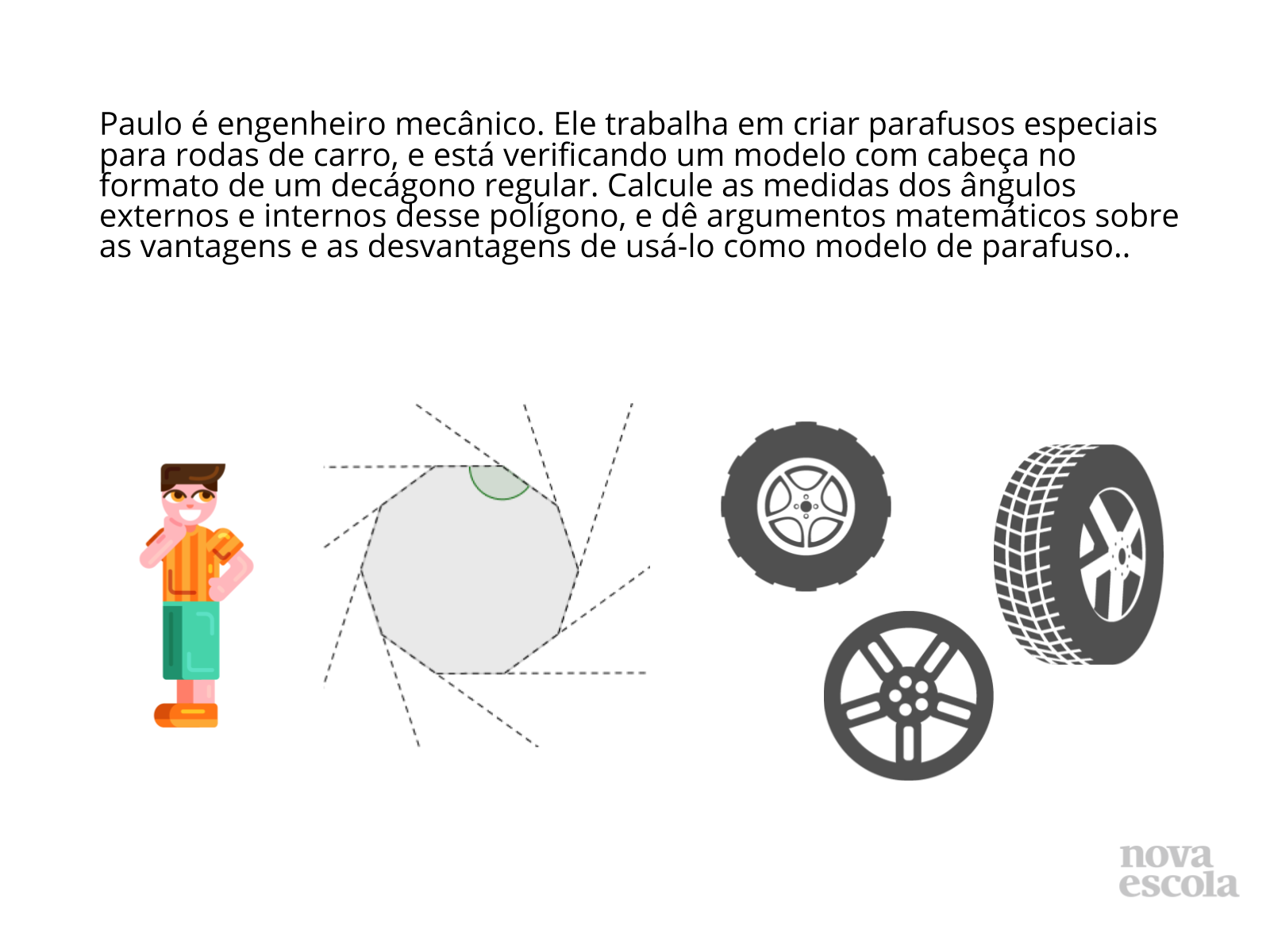
Tempo sugerido: 7 minutos
Orientação: Entregue uma folha de atividade para cada aluno e peça que leiam e a realizem individualmente. Circule para verificar como os alunos estão desenvolvendo o que foi proposto. O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto. No final, reserve um tempo para o registro das soluções na lousa. Propósito: Verificar se os alunos aplicam corretamente os conhecimentos adquiridos sobre o cálculo da medida dos ângulos internos e externos de polígonos regulares numa situação problema envolvendo peças mecânicas, semelhante à estudada na aula.
Materiais complementares para impressão:
Raio X
Sugestão de adaptação para ensino remoto
Código do plano
MAT7_20GEO05
Recursos
- Necessários:
- caderno
- lápis
- lápis de cor
- régua
- grupo de alunos no Whatsapp
- Opcionais:
- Google Sala de Aula
Para este plano, foque na etapa: Atividade Principal
Aquecimento
Compartilhe o questionamento inicial via WhatsApp e peça aos alunos que gravem as suas respostas e compartilhe com o professor.
Atividade principal
Para a realização da atividade principal os alunos precisam ter acesso ao problema proposto. Para isso, fotografe a atividade principal e disponibilize a imagem no grupo de whatsapp para que os alunos possam pensar sobre ele. Oriente-os a filmar ou fotografar as suas estratégias e respostas para compartilhar com o professor e a turma no momento da discussão das soluções.
Discussão das soluções
Professor, caso esteja em uma aula síncrona, realize a discussão das soluções por meio de um debate de ideias, procurando apresentar mais de uma possibilidade de soluções. Nesse momento questione aos alunos. Após fazer essas intervenções e ouvir dos alunos, seja por WhatsApp, Google Sala de Aula ou pelo Meet, por exemplo, sistematize a aula junto aos alunos.
Raio X
A atividade do Raio X pode ser usada como tarefa de casa ou como avaliação da aula. Envie e faça a discussão da mesma forma que fez com a atividade principal. Lembre-se também que há atividades complementares que podem ser enviadas aos alunos como atividades de fixação ou sistematização.
Convite às famílias
A participação das famílias no processo de aprendizagem é de grande importância para o aluno. Porém, ressaltamos que os pais não são professores de matemática e muitos estão ocupados com outras funções em casa. Portanto, indicamos a participação das famílias no compartilhamento e discussão de possíveis soluções para os problemas propostos.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Rosilaine Sanches Martins
Mentor: Fabrício Eduardo Ferreira
Especialista de área: Pricilla Cerqueira
Habilidade da BNCC
(EF07MA22) Calcular medidas de ângulos internos de polígonos regulares, sem o uso de fórmulas, e estabelecer relações entre ângulos internos e externos de polígonos, preferencialmente vinculadas à construção de mosaicos e de ladrilhamentos, à confecção de ferramentas e peças mecânicas, entre outras.
Objetivos específicos
Estabelecer relações entre ângulos internos e externos de polígonos, vinculadas à confecção de ferramentas e peças mecânicas.
Conceito-chave
Ângulos internos de polígonos regulares.
Recursos necessários
- Parafusos e chaves de parafusos de vários tipos;
- Atividades impressas em folhas, coladas no caderno ou não.