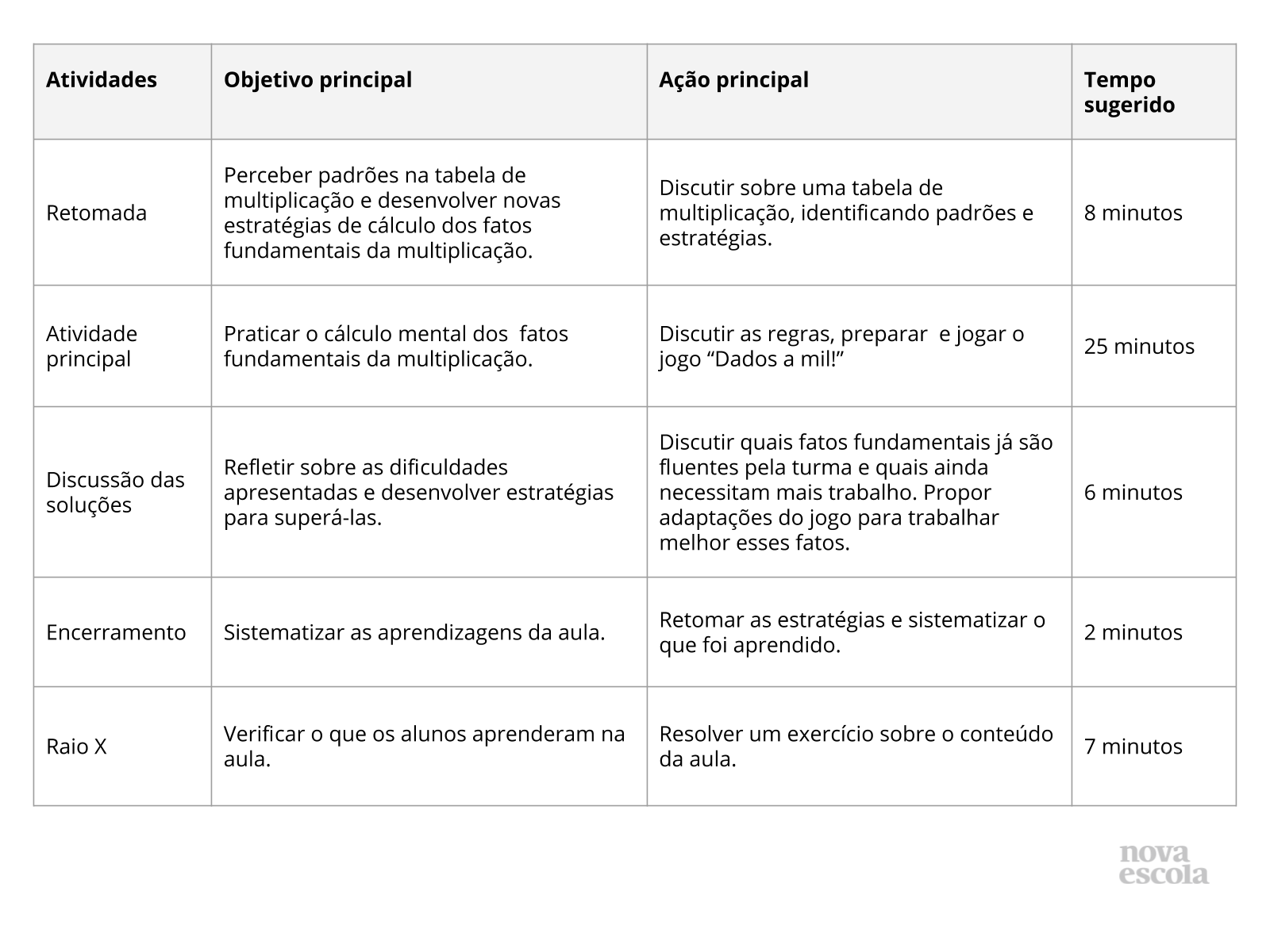
Atividade Principal - Exemplo de Jogo
Plano de Aula
Plano de aula: Fatos fundamentais da multiplicação com o jogo “Dados a Mil!”
Plano 5 de uma sequência de 5 planos. Veja todos os planos sobre Jogos para fluência de fatos fundamentais da multiplicação e divisão
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Andresa Prata Cirino Cuginotti
Mentor: Elisa Greenhalgh Vilalta
Especialista de área: Luciana Tenuta
Habilidades da BNCC
(EF04MA03) Resolver e elaborar problemas com números naturais envolvendo adição e subtração, utilizando estratégias diversas, como cálculo por estimativa, cálculo mental e algoritmos.
(EF04MA04) Utilizar as relações entre adição e subtração, bem como entre multiplicação e divisão, para ampliar as estratégias de cálculo.
(EF04MA05) Utilizar as propriedades das operações para desenvolver estratégias de cálculo.
Objetivo específico
Adquirir fluência com os fatos fundamentais da multiplicação.
Conceito-chave
Fatos fundamentais da multiplicação, cálculo mental, propriedades da multiplicação.
Recursos necessários
Lápis, papel, cartolina.
Vocabulário que será adquirido nesta aula
Multiplicação, tabuada, padrão, cálculo.
Habilidades BNCC:
Objetivos de aprendizagem
Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
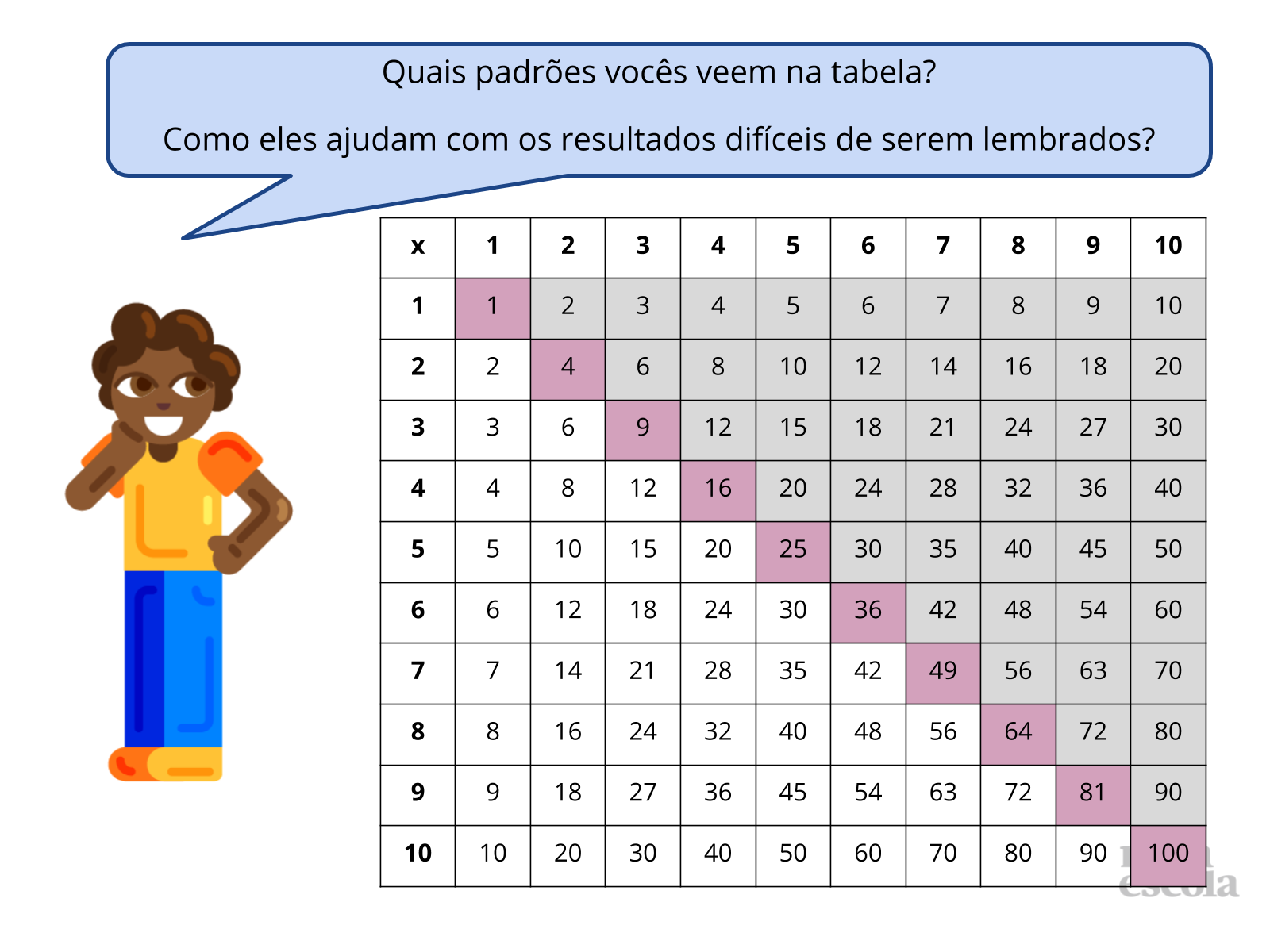
Retomada
Tempo sugerido: 8 minutos
Orientação: Projete ou apresente a tabela em um mural, quadro ou cartolina grande. Leia as perguntas. Explique aos alunos como funciona a tabela, caso eles não a conheçam: Cada quadradinho apresenta o produto dos números que aparecem na linha e na coluna correspondente do quadradinho. Dê um ou dois exemplos: Aponte um quadradinho e diga que ali aquele número é o produto entre tal e tal números, mostrando a linha e a coluna. Peça aos alunos que identifiquem padrões e pergunte como esses padrões nos trazem estratégias para descobrir resultados com os quais ainda temos dificuldades.
Possíveis padrões que serão identificados pelos alunos, entre outros: na tabuada do 5 todos os resultados terminam em 0 ou em 5; multiplicar por 5 é a metade de multiplicar por 10 (propriedade associativa); a tabuada do 4 é o dobro da tabuada do 2 (propriedade associativa); a tabuada do 6 é o dobro da tabuada do 3 (propriedade associativa); a tabuada do 8 é o dobro da tabuada do 4 (propriedade associativa); a tabuada do 7 é a soma das tabuadas do 3 e do 4 (propriedade distributiva); a tabuada do 9 é o triplo da do 3 (propriedade associativa); a tabela é simétrica porque 4 x 5 = 5 x 4 (propriedade comutativa).
Propósito: Perceber padrões na tabela de multiplicação e desenvolver novas estratégias de cálculo dos fatos fundamentais da multiplicação.
Discuta com a turma:
- Quais os produtos mais difíceis de serem lembrados?
- Quais padrões podem ser identificados na tabela?
- Como é possível descobrir um produto que não sabemos a partir de outros que dominamos?
- Quais estratégias podem ser utilizadas quando não sabemos um resultado?
- Alguém gostaria de explicar sua estratégia para os colegas?
Material complementar para o professor
- Leia o capítulo 11 (Ajudando as Crianças a Dominar os Fatos Fundamentais) de VAN DE WALLE, John A. Matemática no Ensino fundamental: formação de professores e aplicação em sala de aula. Porto Alegre: Artmed, 2009.
- Leia a matéria Um novo jeito de ensinar a tabuada. Disponível em https://novaescola.org.br/conteudo/162/novo-jeito-ensinar-tabuada. Acesso em 15/01/2018.
- Plano de aula sobre a tabela pitagórica (caso queira trabalhar a tabela por mais tempo): http://rede.novaescolaclube.org.br/planos-de-aula/tabela-pitagorica-para-aprender-multiplicacao. Acesso em 16/01/2018.
Atividade principal
Tempo sugerido: 25 minutos
Orientação: Proponha aos alunos o jogo “Dados a mil!”, para a prática dos fatos fundamentais da multiplicação. Se possível, imprima as regras e entregue para os estudantes. Leia as regras com os alunos. Caso não consiga imprimir uma cópia para cada aluno ou uma por dupla, projete, registre no quadro ou em um cartaz onde todos consigam ler. Decida, juntamente com os alunos, quais números devem constar nos dados e quais os fatores pelos quais os resultados devem ser multiplicados. Veja um exemplo. Para essa decisão, reflita com a turma sobre quais os fatos que ainda são menos fluentes e inclua os mesmos no jogo. Não há necessidade de que a turma inteira jogue com os mesmos números. Você pode, e deve, adequar os números às dificuldades de cada um, agrupando os alunos de forma que todos os grupos se sintam desafiados e aprendam com o jogo. Se decidir por grupos diferentes jogarem com diferentes números, complete as regras como um exemplo e depois, com cada grupo, decida os números durante a construção dos dados.
O jogo é uma adaptação do jogo de dados 10.000, também chamado Farkle ou Zilch. É possível que alguns estudantes conheçam o jogo e façam uma relação com ele. Diga que o jogo é uma adaptação, mas que outras regras podem ser incorporadas caso o grupo assim decida. No caso de propostas de mudanças serem feitas, discuta rapidamente o motivo da modificação e consulte a turma antes de mudar. Os alunos devem anotar as modificações nas folhas impressas ou em suas anotações. Eles podem ainda anotar as regras no caderno para poder jogar em outras ocasiões com amigos ou mesmo com a família.
Após a leitura, faça uma jogada demonstrativa na lousa com alunos voluntários e aproveite esse momento para esclarecer eventuais dúvidas sobre as regras e dinâmica do jogo.
Propósito: Compreender as regras de um jogo e discuti-las.
Discuta com a turma:
- O que vocês entenderam das regras apresentadas?
- Alguém já conhecia ou ouviu falar de um jogo semelhante a esse?
- Alguém gostaria de propor alguma outra regra ou modificar alguma das listadas?
- Qual seria o propósito da mudança ou inclusão dessa regra?
- Quais as multiplicações que necessitamos treinar mais? Como incluí-las no jogo?
Materiais complementares
Atividade Principal - Exemplo de Jogo
Atividade Principal - Tabela de Pontuação
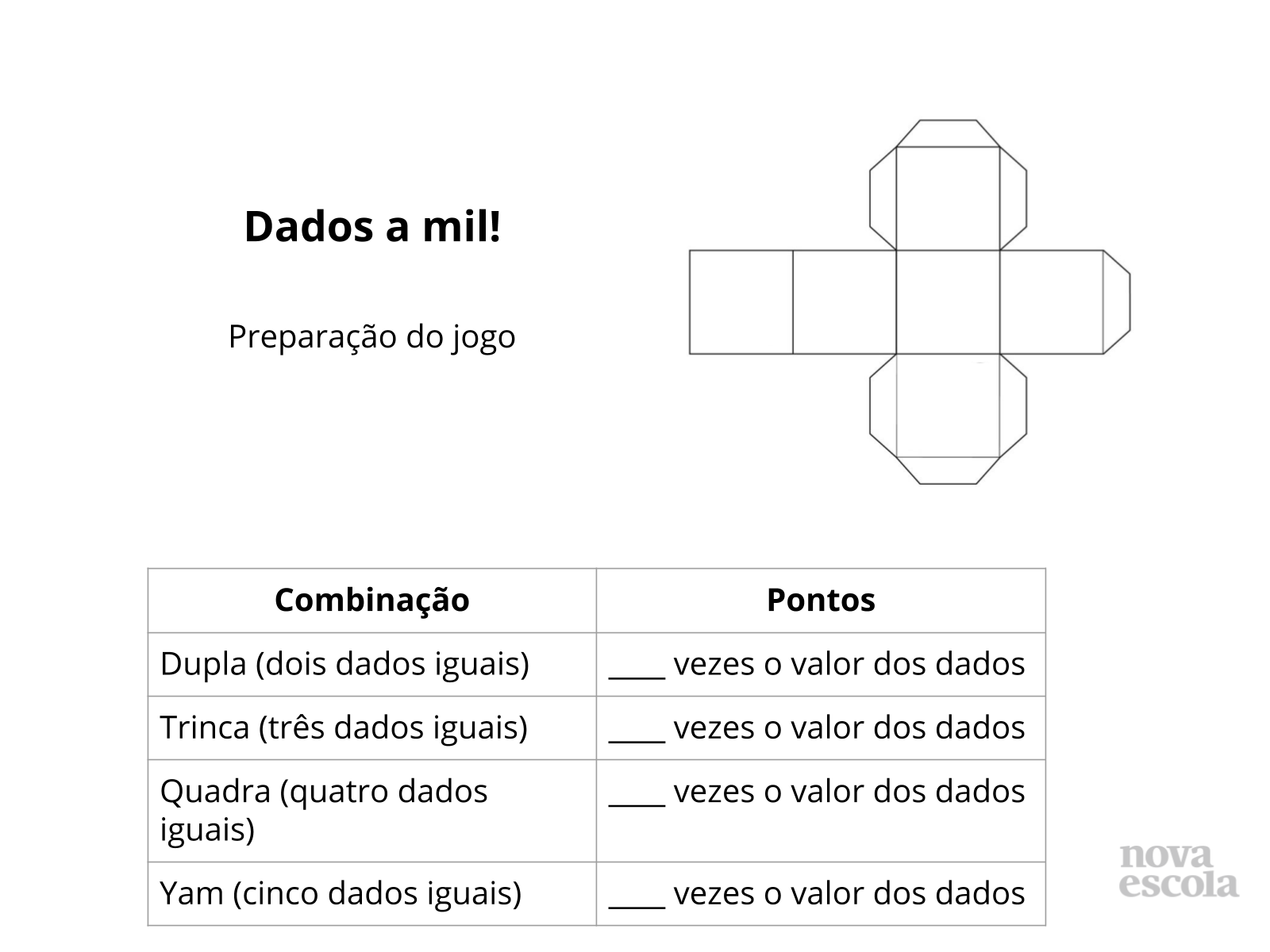
Atividade principal
Tempo sugerido: 25 minutos
Orientação: Organize grupos (2 a 4 alunos) para preparar o jogo e depois jogar. Imprima os dados em branco, se possível em um papel de maior gramatura. Cada grupo necessitará 5 dados. Os dados devem ser completados com os números (entre 1 e 9) decididos pela turma ou pelos grupos. Os 5 dados devem conter os mesmos números. Imprima a tabela com os fatores de multiplicação e peça para que os alunos preencham com os fatores decididos pela turma ou por cada grupo. Embora o jogo seja relativamente simples, pode ser que os alunos não se lembrem facilmente de qual o fator pelo qual devem multiplicar de acordo com os resultados dos dados (mesmo porque esses fatores podem variar de acordo com o grupo ou com o momento). A tabela com esses fatores deve estar acessível durante o jogo.
Propósito: Preparar o jogo.
Discuta com a turma:
- Quais as multiplicações que necessitamos treinar mais?
- Como incluir essas multiplicações no jogo?
Materiais complementares
Atividade Principal - Exemplo de Jogo
Atividade Principal - Tabela de Pontuação
Resolução da Atividade Principal
Material complementar para o professor:
- Leia a matéria As trocas que fazem a turma avançar. Disponível em https://novaescola.org.br/conteudo/366/as-trocas-que-fazem-a-turma-avancar. Acesso em 28/12/17.
- Leia a matéria Como agrupo meus alunos? Disponível em https://novaescola.org.br/conteudo/1475/como-agrupo-meus-alunos. Acesso em 28/12/17.
Atividade principal

Tempo sugerido: 25 minutos
Orientação: Proponha aos grupos que joguem o jogo independentemente. Deixe disponível nas mesas papel e lápis para a anotação dos pontos e para o caso de algum aluno necessitá-los para fazer os cálculos. Se necessário, deixe disponível também a tabela de multiplicação para consulta em um primeiro momento. Enquanto os alunos jogam, circule entre eles, observando como eles jogam e calculam. Preste atenção especial a como os alunos, quando discordam em relação a um resultado, explicam suas estratégias uns aos outros. Se não explicarem, intervenha, pedindo que expliquem até que todos do grupo compreendam qual a resposta correta e como chegar nela. Em caso de dúvidas nos cálculos, peça para que conversem com os colegas para tentar resolver. Entre rodadas, converse com os alunos sobre as perguntas sugeridas abaixo. Faça anotações sobre o que observar e sobre o que os alunos falarem nesse momento. Utilize o guia de intervenção para analisar dificuldades e realizar intervenções.
Propósito: Praticar os fatos fundamentais da multiplicação.
Discuta com a turma:
- Houve algum cálculo que vocês não sabiam?
- Quais estratégias usaram para resolvê-lo?
- Vocês já discordaram sobre algum resultado?
- Se sim, como resolveram essa discordância?
- Vocês estão compartilhando estratégias?
- Quem aprendeu alguma estratégia nova com um colega?
- Você já está mais seguro com os resultados de alguma multiplicação que julgava mais difícil?
Materiais complementares
Atividade Principal - Exemplo de Jogo
Atividade Principal - Tabela de Pontuação
Resolução da Atividade Principal
Material complementar para o professor:
- Leia a matéria Escrita profissional: a importância dos registros feitos pelos professores. Disponível em: https://novaescola.org.br/conteudo/441/escrita-profissional. Acesso em 17/01/18.
Discussão da solução

Tempo sugerido: 6 minutos
Orientação: Converse com os alunos sobre quais estratégias eles utilizaram quando se depararam com uma multiplicação que não sabiam automaticamente. Peça que compartilhem estratégias usadas durante o jogo. Peça que 3 ou 4 alunos compartilhem como resolveram as dificuldades ou como um colega lhe explicou os possíveis equívocos. Pergunte se alguém usou diferentes estratégias dependendo dos números envolvidos. Peça que compartilhem. Nesse momento, retome as anotações que você fez durante a observação do jogo e convide alunos específicos a compartilharem suas estratégias e dificuldades, de acordo com o que foi observado. Dessa forma, haverá uma variedade a ser discutida. Anote os nomes dos alunos que compartilharam suas resoluções próximo ao registro da estratégia. Se possível, deixe esse registro exposto na sala.
Propósito: Discutir estratégias para se saber resultados de multiplicações ainda não fluentes.
Discuta com a turma:
- Quais estratégias você utilizou durante o jogo?
- A estratégia que você encontrou foi bem sucedida?
- O que você aprendeu com a sua estratégia?
- Em que situação cada estratégia foi mais utilizada?
- Quais as dificuldades que apareceram?
- Como as dificuldades foram resolvidas?
- Quais os fatos fundamentais que vocês já dominam?
- Quais ainda necessitam mais tempo para saber o resultado?
- Algum fato fundamental não era fluente e agora já é?
Encerramento

Tempo sugerido: 2 minutos
Orientações: Encerre a atividade retomando com os estudantes as atividades feitas nesta aula e o que foi aprendido. Retome com os alunos as estratégias elencadas por eles e converse sobre quando é possível utilizá-las e quando é necessário realizar os cálculos para poder comparar os resultados. Anote as contribuições na lousa, de forma que fiquem visíveis para todos.
Propósito: Sistematizar a aprendizagem, revisando o que foi estudado.
Discuta com a turma:
- O que fizemos nessa aula?
- O que aprendemos ou praticamos nessa aula?
- Quais estratégias conhecemos para comparar resultados de divisões?
- Quando essas estratégias podem ou não ser utilizadas?
- Como sabemos qual o maior resultado quando não podemos utilizar essas estratégias?
Raio X

Tempo sugerido: 7 minutos.
Orientações: Para finalizar a aula, apresente o problema aos alunos. Você poderá projetá-lo, imprimi-lo ou escrevê-lo na lousa. Peça aos alunos que leiam e resolvam individualmente. Circule para verificar como os alunos estão realizando os cálculos. O Raio X é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. No final, reserve um tempo para um debate coletivo registrando as soluções no quadro.
Propósito: Verificar o que os alunos aprenderam na aula.
Discuta com a turma:
- Como vocês resolveram o problema?
- Existem diferentes formas de resolver esse problema?
- Qual a estratégia mais prática e rápida para resolver esse problema?
- Alguém pensou de uma outra forma?
Materiais complementares:
Sugestão de adaptação para ensino remoto
Código do plano
MAT4_06NUM_05
Recursos
USAR APENAS FERRAMENTAS EM PORTUGUÊS E GRATUITAS
- Necessários: (apenas se forem absolutamente indispensáveis; caso contrário, inserir todos como opcionais)
- Opcionais: Google Documentos, Google Meet, app de lançamento de dados (link disponível na adaptação), Google Formulários.
Para este plano, foque na etapa Atividade Principal.
Retomada
Proponha aos alunos que respondam às questões presentes nas orientações ao professor, no campo “Discuta com a turma”, para que a turma use o quadro pitagórico como base para as respostas. As respostas podem ser dadas usando o Google Documentos, em que os alunos criam uma cópia para eles do arquivo base fornecido pelo professor (que já contém o quadro pitagórico e as questões) ou por escrito em folha impressa (também contendo o quadro e as questões).
Atividade principal
Proponha aos alunos que joguem o jogo aqui proposto com um dos seus familiares ou com um colega via Google Meet. É possível jogar com dados físicos (sejam eles comprados ou montados pelo próprio aluno) ou com o auxílio de um aplicativo de lançamento de dados. Segue link para app de lançamento de dados: https://play.google.com/store/apps/details?id=com.martianlab.dice.lite&hl=pt_BR
Discussão das soluções
Pedir aos alunos que façam um registro das rodadas que foram jogadas para que possam analisá-las antes de jogar pela segunda, terceira ou quarta vez que o aluno jogar. Esse registro pode ser feito usando o Google Documentos ou o registro escrito.
Sistematização
Não há.
Encerramento
Propor aos alunos que façam um registro coletivo usando o Google Documentos para partilhar estratégias utilizadas nas jogadas.
Raio X
Sugira aos alunos que respondam à situação problema proposta no slide e aos problemas indicados no arquivo de atividade complementar disponível nas orientações ao professor. Você pode usar o próprio arquivo impresso ou transpor as perguntas para o Google Formulários.
Convite às famílias
Convide a família a jogar o jogo indicado na etapa de Atividade Principal para que haja interação entre a família e o aluno, seja usando o recurso digital ou os dados físicos.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Andresa Prata Cirino Cuginotti
Mentor: Elisa Greenhalgh Vilalta
Especialista de área: Luciana Tenuta
Habilidades da BNCC
(EF04MA03) Resolver e elaborar problemas com números naturais envolvendo adição e subtração, utilizando estratégias diversas, como cálculo por estimativa, cálculo mental e algoritmos.
(EF04MA04) Utilizar as relações entre adição e subtração, bem como entre multiplicação e divisão, para ampliar as estratégias de cálculo.
(EF04MA05) Utilizar as propriedades das operações para desenvolver estratégias de cálculo.
Objetivo específico
Adquirir fluência com os fatos fundamentais da multiplicação.
Conceito-chave
Fatos fundamentais da multiplicação, cálculo mental, propriedades da multiplicação.
Recursos necessários
Lápis, papel, cartolina.
Vocabulário que será adquirido nesta aula
Multiplicação, tabuada, padrão, cálculo.










