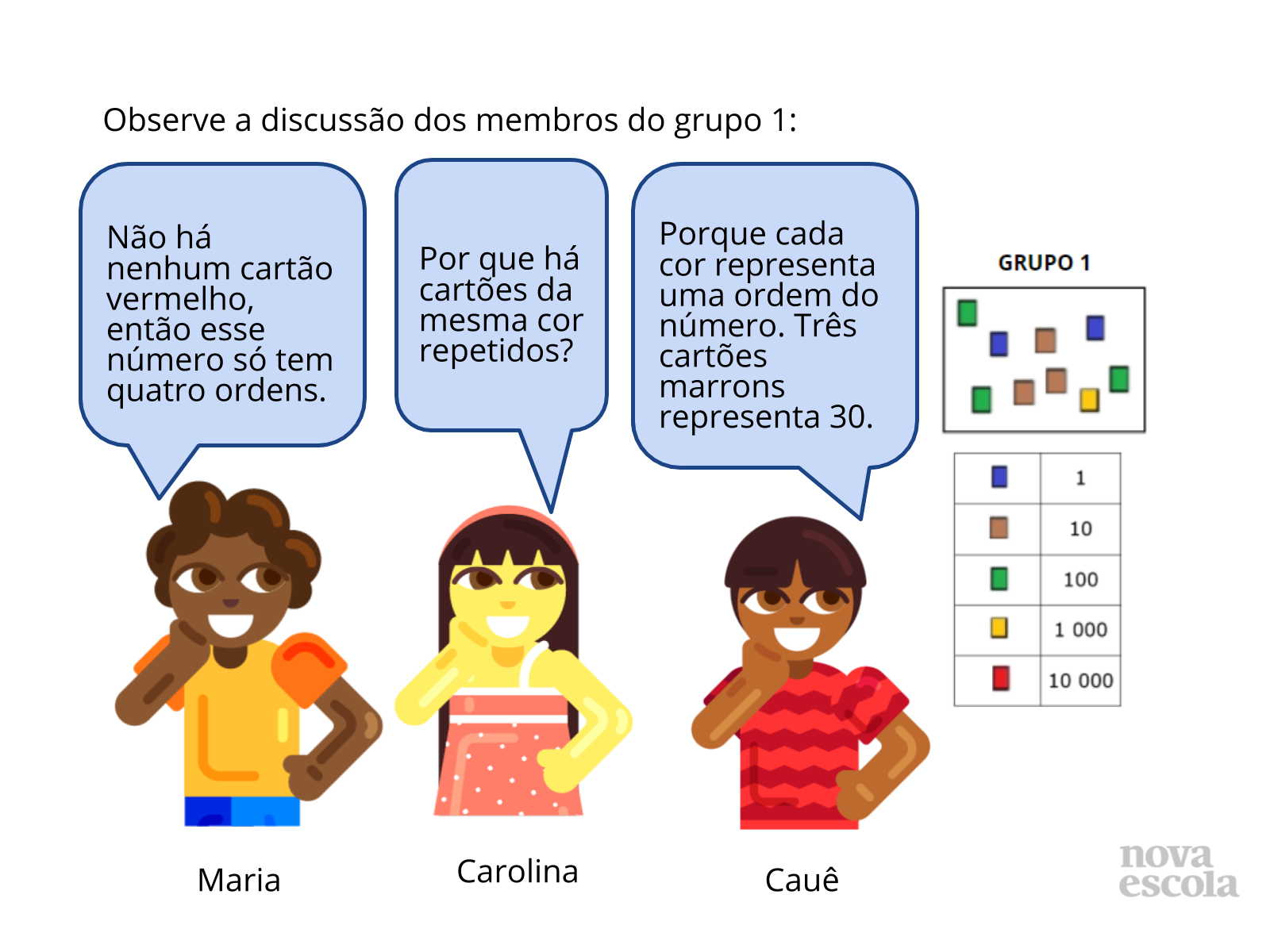
Atividade Principal
Plano de Aula
Plano de aula: Utilizando a calculadora para compreender o Sistema de Numeração Decimal
Plano 5 de uma sequência de 5 planos. Veja todos os planos sobre Composição e decomposição de números naturais
Por: Cíntia Diógenes
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Cíntia Diógenes
Mentora: Elisa Greenhalgh Vilalta
Revisora Pedagógica: Eliane Zanin
Especialista de área: Luciana Tenuta
Habilidade da BNCC
EF04MA02 - Mostrar, por decomposição e composição, que todo número natural pode ser escrito por meio de adições e multiplicações por potências de dez, para compreender o sistema de numeração decimal e desenvolver estratégias de cálculo.
Objetivos específicos
- Compor e decompor números naturais, baseado em seu valor posicional, que pode ser descrito por meio de adições e multiplicações por potências de dez.
- Compreender a função do zero no Sistema de Numeração Decimal e utilizá-lo adequadamente.
Conceito-chave
Propriedades do Sistema de Numeração Decimal.
Composição e decomposição de números naturais.
Uso e função do zero.
Recursos necessários
- Folha de papel A4 branca;
- Atividades impressas em folhas, coladas no caderno ou não;
- Folhas de papel (para registro das estratégias);
- Canetas ou lápis e borracha;
- Calculadoras.
Habilidades BNCC:
Objetivos de aprendizagem
- Compor e decompor números naturais, baseado em seu valor posicional, que pode ser descrito por meio de adições e multiplicações por potências de dez.
- Compreender a função do zero no Sistema de Numeração Decimal e utilizá-lo adequadamente.
Resumo da aula
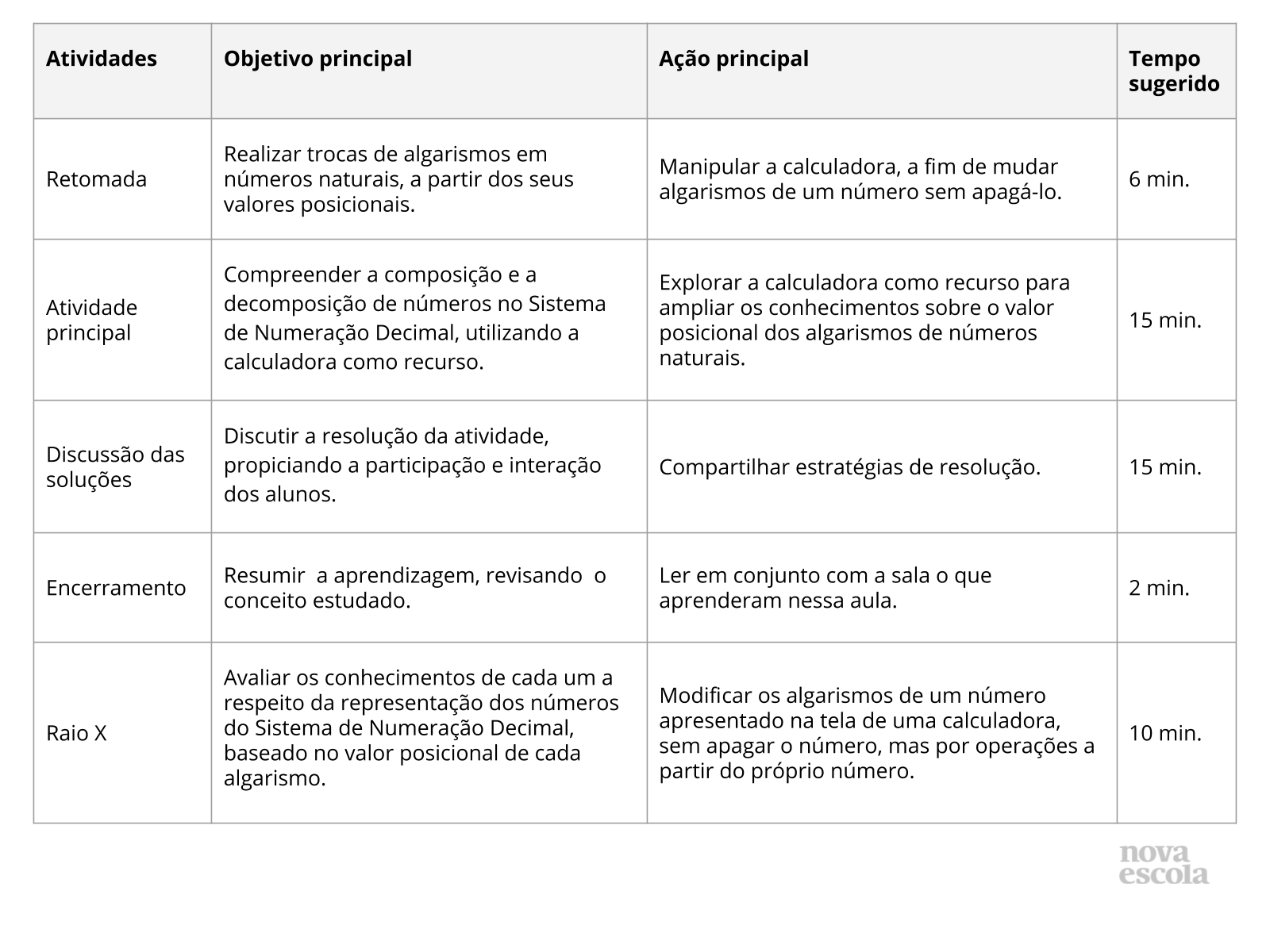 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada

Tempo previsto: 6 minutos.
Orientações: Distribua a turma em duplas e disponibilize uma calculadora por dupla. Prepare esse recurso com antecedência, seja solicitando-as à escola ou pedindo, em um dia anterior, que as próprias crianças tragam de casa, na data da aula. Para iniciar a atividade, pode ser dado um minuto para que as duplas se apropriem do recurso, manuseando a calculadora livremente, observando a disposição dos botões e levantando alguma dúvida para o professor. Após esse momento, apresente o problema do slide e solicite que as crianças digitem nas calculadora o número 20 000. Permita que as duplas discutam acerca de estratégias que levem ao resultado esperado e depois dialoguem e reflitam sobre essas estratégias e o porquê das duplas terem tido determinado raciocínio. Verifique as diferenças e semelhanças entre as estratégias e confirmar se elas, de fato, fazem aparecer na tela da calculadora o número solicitado. Permita que as crianças expressem suas observações sobre a relação dessa atividade com as propriedades do Sistema de Numeração Decimal, estudados em aulas anteriores.
Propósito: Realizar trocas de algarismos em números naturais, a partir dos seus valores posicionais.
Discuta com a turma:
- Você já utilizou uma calculadora? Com qual objetivo?
- Para que serve uma calculadora?
- Você conhece as teclas de uma calculadora comum? Quais você conhece? Quais você não conhece?
- Quais teclas da calculadora você digitou para que aparecesse na tela o número 20 000?
- Para que venha aparecer o número 50 000, qual algarismo será trocado? Esse algarismo está em que ordem?
- Qual o valor posicional do algarismo 2 no número 20 000?
- Qual o valor posicional do algarismo 5 no número 50 000?
- Que operação é necessária realizar na calculadora para que apareça o número 50 000 na tela da calculadora, a partir do número 20 000, sem apagar esse número?
- Explique a estratégia que você e sua dupla pensaram para alcançar esse resultado?
- Quais dificuldades vocês enfrentaram para concluir essa atividade e como vocês superaram essas dificuldades?
Resposta esperada:
Espera-se que as duplas percebam que para que fique registrado o número 50 000 na tela da calculadora, a partir do número 20 000, sem apagá-lo, é necessário que se acrescente 30 000 ao número original.
Atividade principal

Tempo sugerido: 15 minutos.
Orientações: Imprima a atividade e entregue -a para cada dupla. Proponha que as crianças, ainda em duplas, digitem o número apresentado no slide em suas calculadoras e leiam por extenso, identificando a ordem e o valor posicional de cada algarismo. Após esse momento, disponibilize de cinco a sete minutos para que as duplas tracem estratégias para responderem a cada item solicitado na atividade. Peça que após solucionarem cada item, a dupla registre em um papel o raciocínio desenvolvido para solucionarem o item, e a resposta encontrada. Caminhe por entre as duplas, verificando as principais dificuldades que estão enfrentando, e mediando, conforme a necessidade, a fim de levar as crianças a uma reflexão e, consequentemente, à compreensão da atividade. Explique que quando todas as duplas tiverem finalizado será aberta uma discussão com toda a turma envolvida, sob a mediação do professor.
Utilize o guia de intervenções para refletir sobre as possíveis dificuldades ou os possíveis erros que as crianças podem apresentar ao tentar resolver a situação -problema e quais intervenções serão necessárias para a promoção da aprendizagem da turma.
Propósito: Compreender a composição e a decomposição de números no Sistema de Numeração Decimal, utilizando a calculadora como recurso.
Discuta com a turma:
- Quais botões da calculadora você precisou digitar para aparecer o número apresentado na atividade em sua tela?
- Quais os algarismos que compõem esse número?
- Em que ordem esses algarismos estão posicionados?
- Como lemos esse número por extenso?
- Você poderia decompor esse número? Qual o valor posicional de cada algarismo?
- Quais estratégias você e sua dupla utilizaram para solucionarem os itens da atividade? Por que utilizaram essa estratégia?
- As estratégias de todas as duplas foram iguais ou algumas foram diferentes? Quais as diferenças e qual a consequência disso para o resultado da atividade?
- Qual o item mais simples de resolver? E qual o mais difícil? Por quê?
Material Complementar:
Material complementar para o professor:
Usar ou não a calculadora em sala de aula?
Fonte:
http://mathema.com.br/reflexoes/usar-ou-nao-a-calculadora-em-sala-de-aula/
A calculadora deve ser usada em sala de aula?
Fonte:
https://novaescola.org.br/conteudo/2682/a-calculadora-deve-ser-usada-em-sala-de-aula
Discussão de soluções
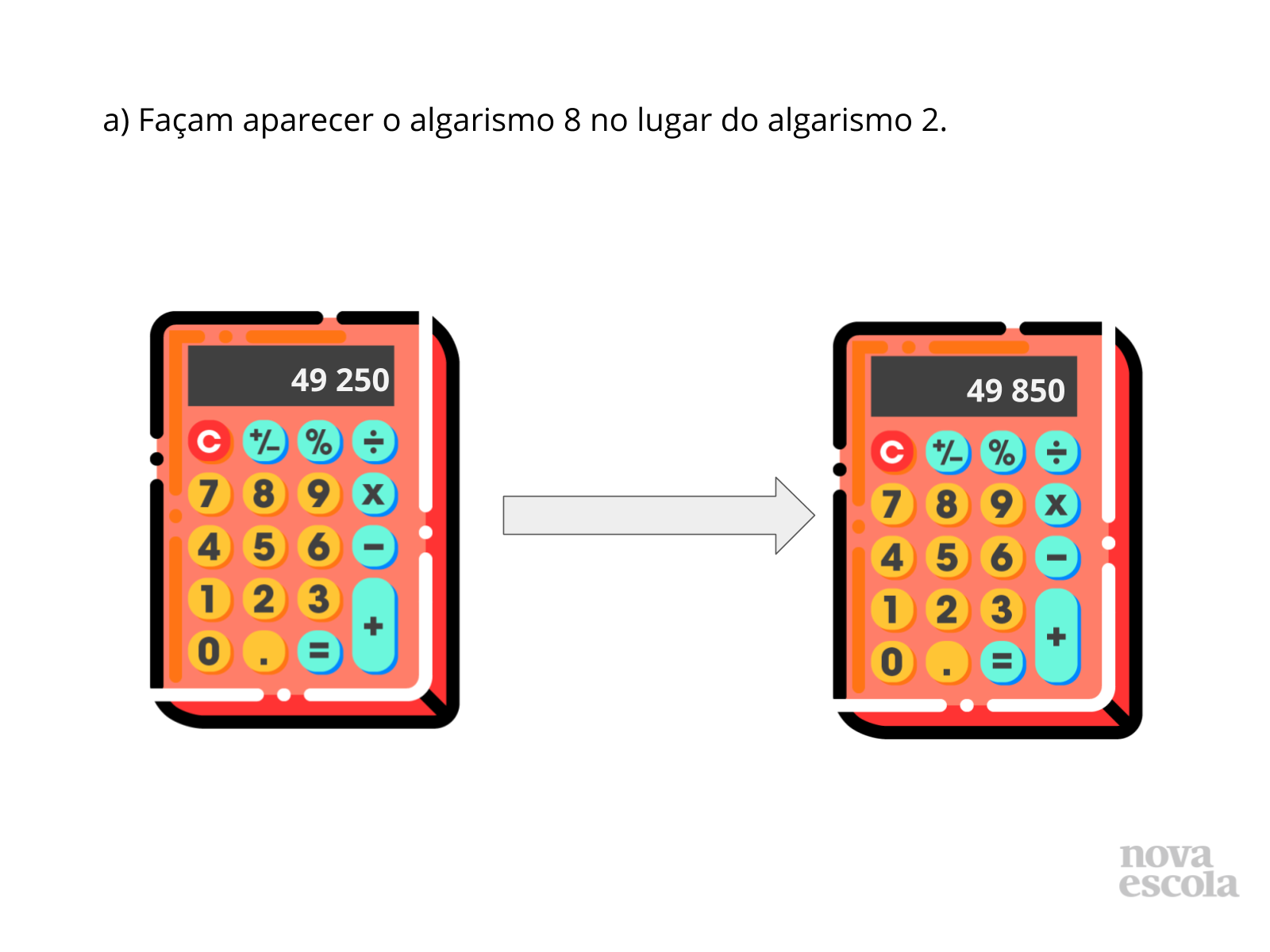
Propósito: Discutir a resolução da atividade, propiciando a participação e interação dos alunos.
Orientações: Peça que as duplas expliquem como resolveram cada situação. Permita que compartilhem as diferentes estratégias usadas. Esteja atento às estratégias que as duplas usaram o e faça as intervenções conforme veja necessidade ou forem surgindo dúvidas. É esperado que as crianças tenham localizado a ordem do algarismo 2 no número original e verificado o quanto deveria ser acrescentado a essa ordem para que o algarismo 2 passe a ser o algarismo 8. Esse item da atividade só pode ter sido feito corretamente se os alunos estiverem certos quanto ao valor posicional dos algarismos, caso contrário, pode ter acontecido de algumas duplas alegarem que para aparecer o algarismo 8 no lugar do algarismo 2, foi necessário acrescentar 6 unidades, o que é incorreto. Por isso, também é importante que as crianças verifiquem se suas estratégias foram corretas, realizando a operação em suas calculadoras.
Discuta com a turma:
- Qual algarismo será trocado nesse item? Em qual ordem ele se encontra?
- Qual o valor posicional do algarismo 2 no número original?
- O algarismo 2 deve ser trocado por qual algarismo?
- Em qual ordem o algarismo 8 aparecerá após a troca?
- Qual seria o valor posicional do algarismo 8 no número final?
- O que deve ser feito para realizar essa troca?
- Houve alguma dificuldade enfrentada por você e sua dupla para responder a esse item? Qual? Como vocês conseguiram identificar essa dificuldade e como a superaram?
Material Complementar:
Resolução da Atividade Principal
Discussão de soluções
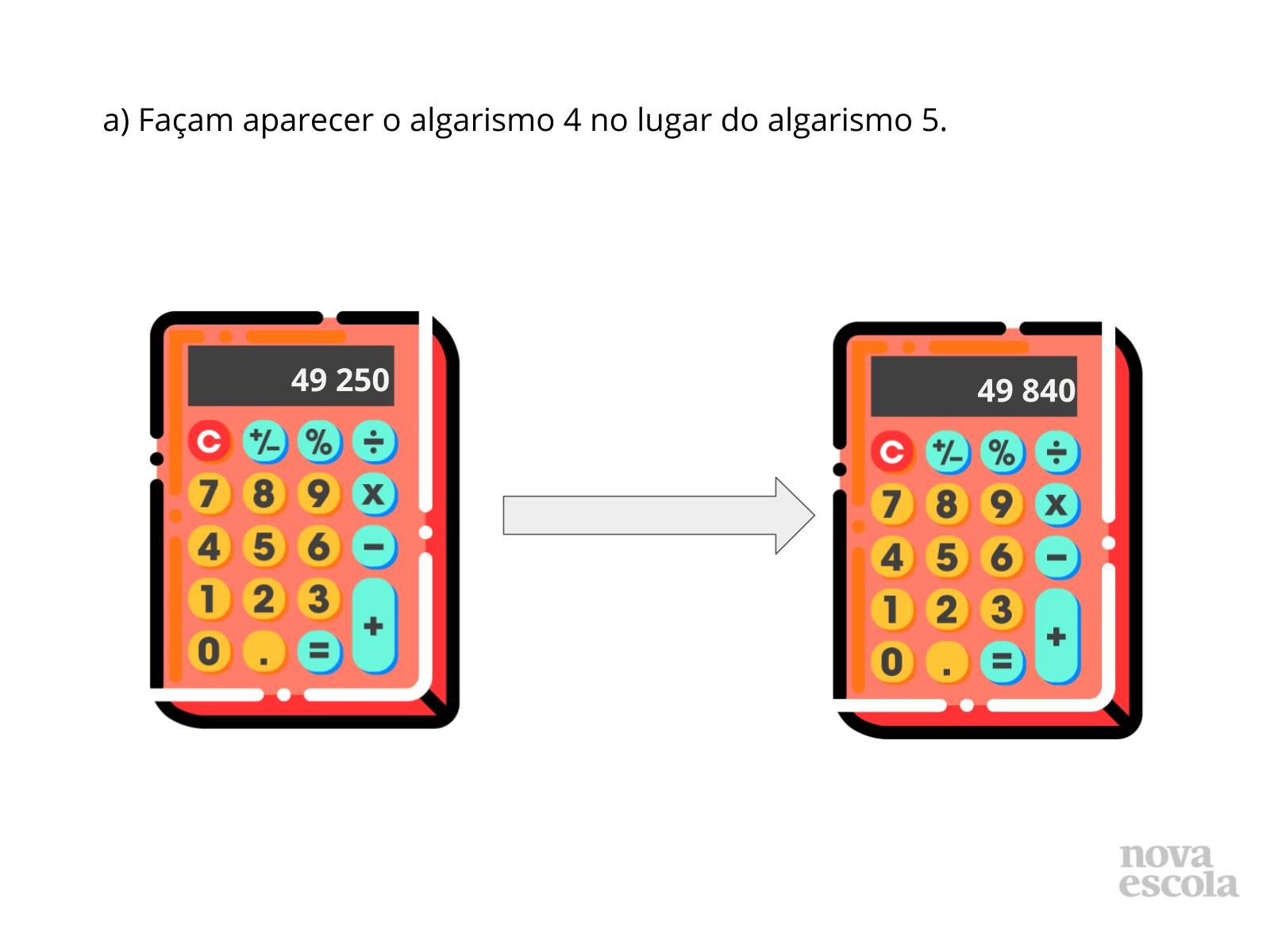
Propósito: Discutir a resolução da atividade, propiciando a participação e interação dos alunos.
Orientações: O percurso trilhado para o desenvolvimento deste item junto às crianças deve ter sido semelhante ao item anterior. Peça que as duplas leiam novamente a tela da calculadora e expliquem como fizeram para aparecer o algarismo 4 no lugar do algarismo 5. Mais uma vez as duplas discutem qual foi a melhor estratégia verificando similaridades e diferenças. Registre na lousa o que as crianças descobriram sobre como realizaram essas mudanças nos algarismos nos dois primeiros itens da atividade. É esperado que os alunos observem que, no primeiro item, foi necessário acrescentar 6 centenas ou 600 unidades ao número original e que, no segundo item, foi necessário retirar 1 dezena ou 10 unidades do número original para alcançar o resultado esperado.
Discuta com a turma:
- Qual algarismo será trocado nesse item? Em qual ordem ele se encontra?
- Qual o valor posicional do algarismo 5 no número original?
- O algarismo 5 deve ser trocado por qual algarismo?
- Em qual ordem o algarismo 4 aparecerá após a troca?
- Qual seria o valor posicional do algarismo 4 no número final?
- O que deve ser feito para realizar essa troca?
- Qual a diferença que as duplas puderam observar sobre a estratégia de resolução do primeiro item para a do segundo?
- Houve alguma dificuldade enfrentada por você e sua dupla para responder a esse item? Qual? Como vocês conseguiram identificar essa dificuldade e como a superaram?
Discussão de soluções

Propósito: Discutir a resolução da atividade, propiciando a participação e interação dos alunos.
Orientações: É esperado que, na etapa da resolução da atividade, as duplas já tenham autonomia para verificar em qual ordem o algarismo que deve ser modificado se posiciona e quais os valores devem ser retirados ou acrescentados. Esse item diferencia-se dos anteriores, pois solicitou não que o algarismo fosse trocado, mas questionou o quanto teria que adicionar ao algarismo zero sem modificar os outros algarismos. Esse foi o momento das crianças retomarem as propriedades do Sistema de Numeração Decimal, mais especificamente os agrupamentos e as trocas. Peça que as crianças digitem na tela da calculadora zerada o número 49 250 novamente e identifiquem onde se posiciona o algarismo zero. Por fim, sob a mediação do professor, toda a turma discute e registra na lousa as conclusões às quais a turma chegou nesse item. É esperado que a turma verifique que como o algarismo zero se posiciona na ordem das unidades, é possível que se acrescente de 1 a 9 unidades a esse número para que o algarismo que sofra modificações seja somente o zero. Acima desse valor, será necessário agrupar as unidades e realizar a troca de ordens, o que resultaria na mudança de valor de algarismos de outras ordens. É importante que as crianças cheguem a essa conclusão a partir das discussões entre os colegas e a mediação do professor e que registre essa aprendizagem estruturando um pequeno texto explicativo, com palavras e expressões que sejam compreensíveis por elas e conceitualmente corretos.
Discuta com a turma:
- Qual algarismo deve ser modificado nesse item? Em que ordem ele se encontra?
- Qual o valor posicional do algarismo zero no número original?
- Em que o terceiro item diferencia-se dos dois anteriores?
- Quantas unidades devem ser acrescentadas ao algarismo zero para que somente ele se modifique?
- O que acontece se for acrescentada mais do que nove unidades a esse número? O resultado fica de acordo com as orientações da atividade? Por quê?
- Houve alguma dificuldade enfrentada por você e sua dupla para responder a esse item? Qual? Como vocês conseguiram identificar essa dificuldade e como a superaram?
Discussão de soluções

Propósito: Discutir a resolução da atividade, propiciando a participação e interação dos alunos.
Orientações: Nesse item, as crianças tiveram que descobrir valores que elas teriam que adicionar ou subtrair do algarismo 9, para que fosse alterado somente ele e não outros algarismos do número. Para isso, solicite que as duplas expliquem como fizeram. É esperado que tenham percebido que o algarismo 9 está localizado na ordem das unidades de milhar e que, por isso, os valores a serem subtraídos do valor original serão sempre múltiplos de
1 000. As crianças também devem verificar que não é possível acrescentar nenhum valor a esse número, sem modificar nenhum outro, já que, se acrescentarmos o número 1 000, que é o mínimo a ser acrescentado, já será necessário realizar troca de ordens, já modificando outros algarismos. Após todas as duplas terem trocado ideias acerca das estratégias de resolução e a resposta ao qual chegaram, bem como, o que concordam ou discordam das estratégias uma das outras. Finalize discutindo com toda a sala e registrando, com um pequeno texto explicativo, o passo a passo de como chegaram à solução da questão e o resultado.
Discuta com a turma:
- Qual algarismo deve ser modificado nesse item? Em que ordem ele se encontra?
- Qual o valor posicional do algarismo nove no número original?
- Em que o quarto item diferencia-se dos terceiro?
- É possível acrescentar algum valor ao número original para que se tenha um resultado em conformidade ao que o item solicitou? Por quê?
- Quantas unidades de milhar devem ser subtraídas do algarismo nove para que somente ele se modifique?
- Houve alguma dificuldade enfrentada por você e sua dupla para responder a esse item? Qual? Como vocês conseguiram identificar essa dificuldade e como a superaram?
- Ao discutir a estratégia com a sala, que descobertas você e sua dupla fizeram?
Encerramento

Tempo sugerido: 2 minutos.
Orientações: Encerre a atividade retomando com os estudantes os conceitos estudados nesta aula.
Propósito: Resumir a aprendizagem, revisando o conceito estudado.
Raio X

Orientações: Essa atividade busca verificar a compreensão das crianças acerca do valor posicional de cada algarismo de um número e propõe que, a partir de um número pré-existente, o aluno transforme-o em outro número modificando o valor de cada algarismo. A atividade deve ser realizada individualmente. É interessante observar a estratégia que cada criança usa e o caminho trilhado por ela, para alcançar a resolução da questão. Ao final, conforme a necessidade, utilize a calculadora para verificar as respostas elaboradas por cada criança e promover uma discussão em cima disso. O Raio-x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. No final, reserve um tempo para um debate coletivo registrando as soluções na lousa.
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante e avaliar os conhecimentos de cada um a respeito da representação dos números do Sistema de Numeração Decimal, baseado no valor posicional de cada algarismo.
Discuta com a turma:
- Em quais ordens estão posicionados os algarismos 5 e 4 no número representado?
- Quais os seus valores posicionais?
- Qual será o número formado, quando trocarmos os algarismo 5 e 4, pelos algarismos 7 e 8? Como lemos esse número?
- Qual estratégia você utilizou para chegar ao número solicitado na questão?
Materiais Complementares:
Resolução da Atividade Complementar
Para os Alunos
Para o Professor
Sugestão de adaptação para ensino remoto
Código do plano
MAT4_02NUM_05
Recursos
USAR APENAS FERRAMENTAS EM PORTUGUÊS E GRATUITAS
- Necessários: (apenas se forem absolutamente indispensáveis; caso contrário, inserir todos como opcionais) calculadora (física ou digital)
- Opcionais: Google Meet, Google Apresentações, Google Documentos.
Para este plano, foque na etapa Atividade Principal.
Retomada
Usando a calculadora já instalada no computador ou do celular (ou até mesmo uma calculadora simples de mão) o aluno deve responder às questões apresentadas nesta etapa, incluindo as que estão nas orientações ao professor: o professor organiza um roteiro de questões que o aluno deve responder usando o recurso da calculadora. O envio das respostas pode ser feito via Google Formulários ou em folha impressa.
Atividade principal
Usando a mesma proposta apresentada na etapa anterior (Retomada) o professor pode dar os comandos via Google Documentos ou em folha impressa para que o aluno responda às atividades. Com o recurso do Google Documentos, o professor pode solicitar que os alunos façam uma cópia do arquivo disponibilizado, fazendo o registro etapa por etapa das ações com calculadora. O arquivo deve ser compartilhado com o professor após a resolução. Isso permite que o professor insira comentários no arquivo para dar devolutiva ao aluno, de maneira pessoal.
Discussão das soluções
O professor pode organizar uma videoconferência com a turma via Google Meet para discutir as estratégias que cada um utilizou para resolução. Caso o uso do recurso síncrono não seja possível, o professor pode usar alguns exemplos em slides via Google Apresentações ou em folhas impressas para fomentar a reflexão sobre o uso da calculadora neste tipo de procedimento de cálculo.
Sistematização
Não há.
Encerramento
Solicitar que os alunos utilizem a calculadora para criar um exemplo de transformação de um determinado número em outro, seguindo as ideias discutidas neste plano de aula, fazendo seus registros de forma virtual (via Google Documentos) ou em folha impressa.
Raio X
Usar a mesma estratégia de aplicação utilizada na etapa da Atividade Principal, tanto para uso virtual quanto físico das atividades. Importante aplicar também as atividades complementares disponíveis nas orientações ao professor.
Convite às famílias
Convide a família a acompanhar o trabalho do aluno na etapa de Encerramento, auxiliando-o na criação e experimentação de novos comandos.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Cíntia Diógenes
Mentora: Elisa Greenhalgh Vilalta
Revisora Pedagógica: Eliane Zanin
Especialista de área: Luciana Tenuta
Habilidade da BNCC
EF04MA02 - Mostrar, por decomposição e composição, que todo número natural pode ser escrito por meio de adições e multiplicações por potências de dez, para compreender o sistema de numeração decimal e desenvolver estratégias de cálculo.
Objetivos específicos
- Compor e decompor números naturais, baseado em seu valor posicional, que pode ser descrito por meio de adições e multiplicações por potências de dez.
- Compreender a função do zero no Sistema de Numeração Decimal e utilizá-lo adequadamente.
Conceito-chave
Propriedades do Sistema de Numeração Decimal.
Composição e decomposição de números naturais.
Uso e função do zero.
Recursos necessários
- Folha de papel A4 branca;
- Atividades impressas em folhas, coladas no caderno ou não;
- Folhas de papel (para registro das estratégias);
- Canetas ou lápis e borracha;
- Calculadoras.