Resumo da aula
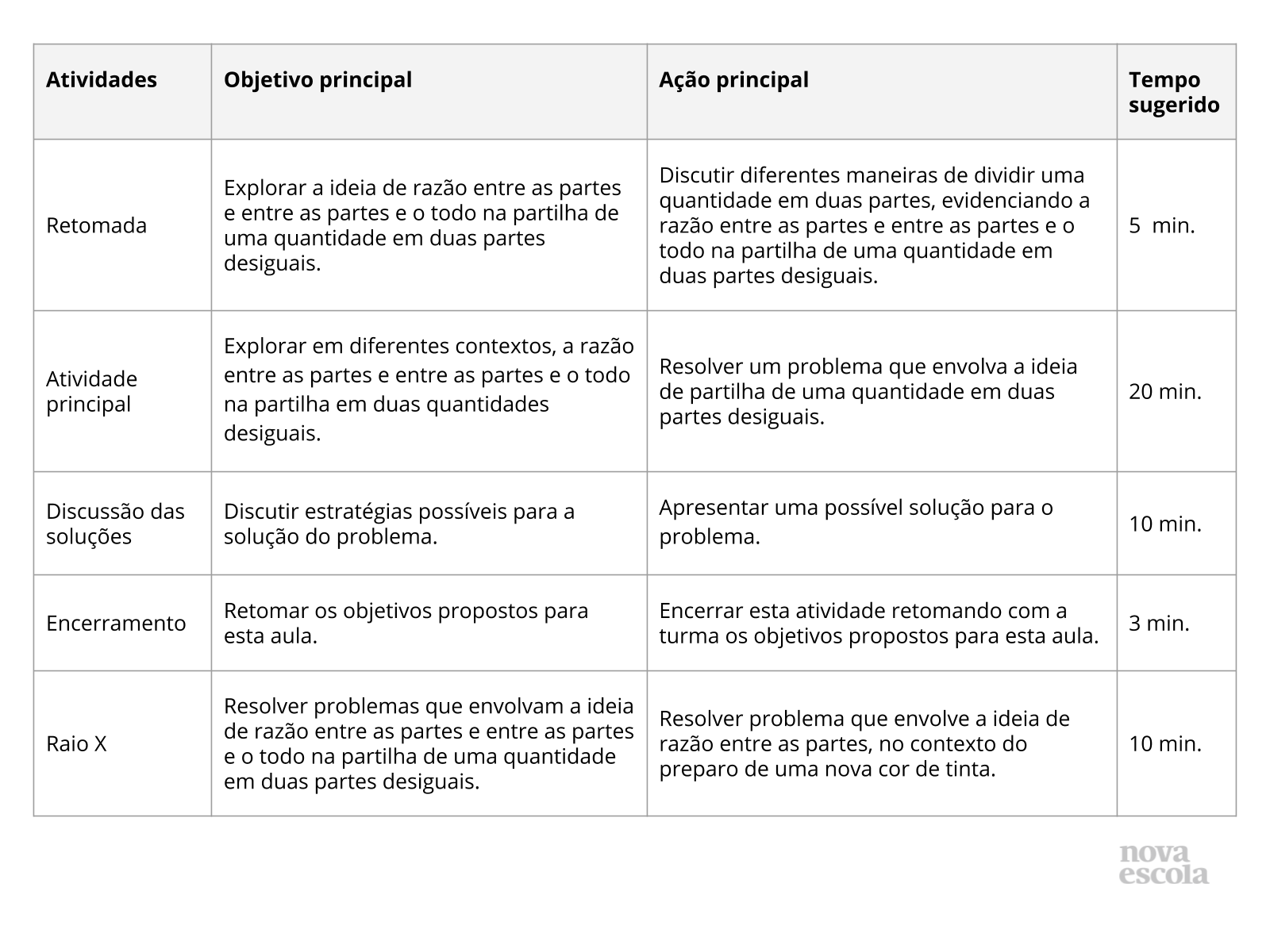
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivos

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia os objetivos para a turma.
Propósito: Compartilhar os objetivos da aula.
Retomada

Retomada
Tempo sugerido: 5 minutos.
Orientação: Projete ou leia o slide lembrando a turma os conceitos-chave envolvidos na situação proposta. Converse com os alunos sobre a possibilidade de dividir uma quantidade em duas partes de diferentes maneiras. Explore as possibilidades indicadas na tabela para a divisão de 40.
Permita que a turma discuta sobre a relação entre as partes e entre as partes e o todo. Participe da discussão, ouvindo e fazendo novas perguntas. Organize a socialização das ideias.
Propósito: Retomar a ideia de que é possível dividir uma quantidade em duas partes de diferentes maneiras, explorando a razão entre as partes e entre as partes e o todo na partilha em duas quantidades.
Discuta com a turma:
- Vocês se lembram do que aprendemos sobre divisão?
- É possível dividir esta quantidade em duas partes?
- Como vocês fariam para dividir esta quantidade em duas partes iguais?
- Há apenas uma maneira de dividir uma quantidade em duas partes?
- É possível dividir uma quantidade em duas partes desiguais?
- O que significa dizer que uma parte é um terço da outra?
- De que outra forma pode ser representada a relação que existe entre as partes?
- O que significa dizer que uma parte é um décimo do todo?
- Há alguma relação entre a outra parte e o todo? Como podemos expressar essa relação?
Atividade principal

Tempo sugerido: 20 minutos.
Orientação: Para realização desta atividade, sugerimos que os alunos estejam em duplas. Para motivar os alunos para a atividade, converse com eles sobre o assunto, pergunte quem já preparou uma receita, se já tomaram suco de acerola, de morango, de morango com acerola, como é o sabor de cada um separado, e como ficariam misturados, como na receita, com mais morango que acerola… enfim, converse com os alunos para que a compreensão do contexto não seja uma dificuldade. Organize as duplas e peça que leiam a atividade com atenção e procurem responder a pergunta proposta, usando a estratégia que preferirem para fazer o que está sendo pedido, desenhos, cálculos, esquemas, tabelas. Peça que respondam as perguntas individualmente e depois discutam na dupla, e assim resolvam a atividade. Reserve um tempo para um debate coletivo e deixe que as duplas compartilhem o que discutiram. Utilize o guia de intervenções para discutir com os alunos as formas e possibilidades de resolução.
Propósito: Perceber que é possível dividir uma quantidade em duas partes de diferentes maneiras, evidenciando a razão entre as partes e entre as partes e o todo na partilha em duas quantidades.
Discuta com a turma:
- O suco foi preparado conforme a receita?
- Quais são as polpas que serão usadas para o preparo do suco?
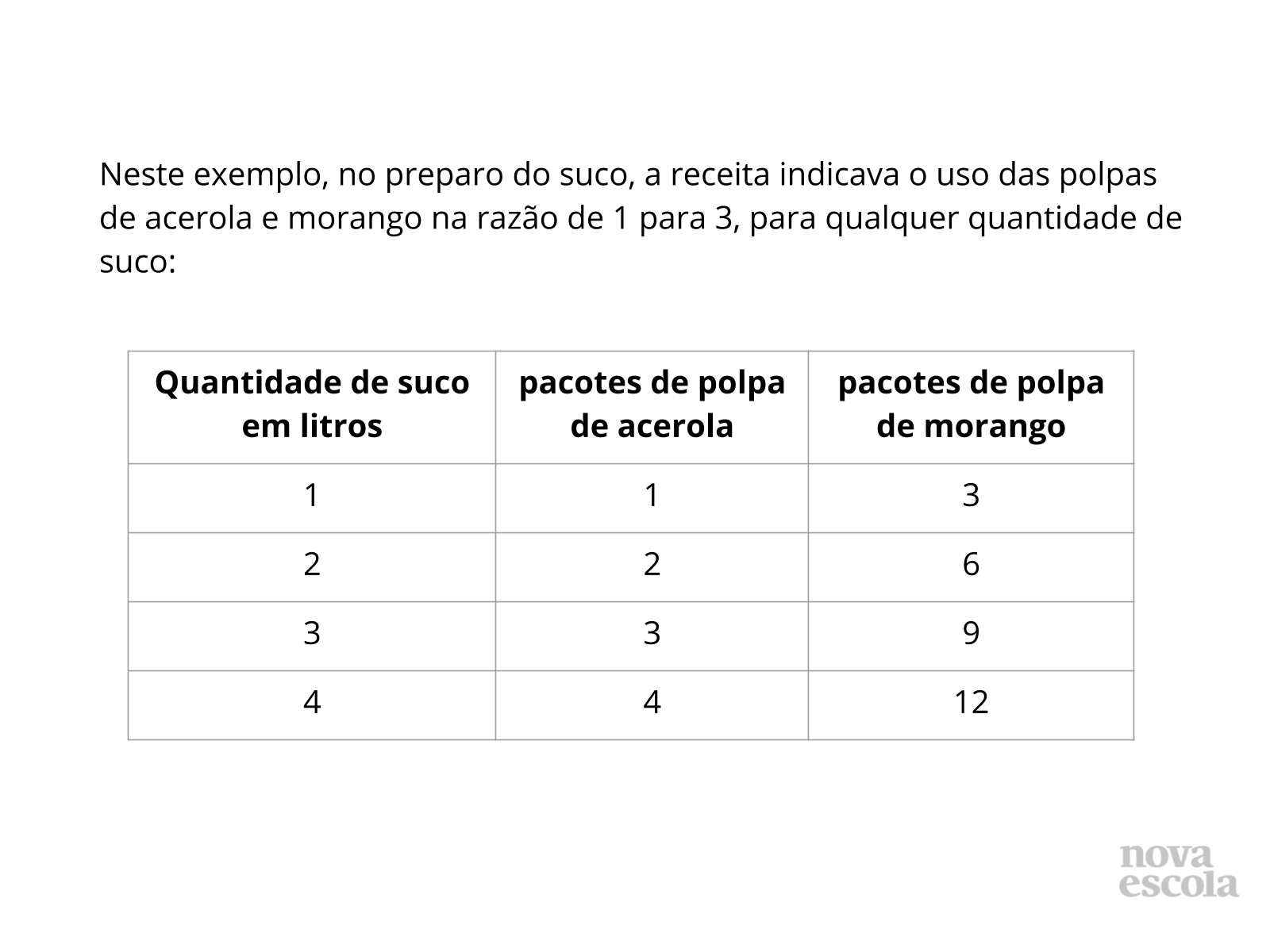
- Quantos pacotes de cada polpa deve ser usado, segundo a receita, para o preparo de um litro de suco?
- Qual a razão entre a quantidade de polpas de cada sabor no preparo de um litro de suco?
- Seguindo esta razão, quanto de cada polpa é necessário para o preparo de dois litros de suco? E para o preparo de três litros de suco? E para o preparo de quatro litros de suco?
- O que é preciso fazer para corrigir o suco preparado, seguindo a razão proposta na receita?
Materiais complementares para impressão:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Discussão da solução

Tempo sugerido: 10 minutos. (Slides 5, 6 e 7)
Orientação: Os alunos discutiram a solução nas duplas, mas neste momento é importante compartilhar com a turma toda, as diferentes estratégias utilizadas para encontrar a solução, mesmo aquelas que tenham fracassado em algum momento. Neste, e nos próximos slides, apresentamos passo a passo, uma possibilidade, talvez a mais recorrente, mas sugerimos que utilize o guia de intervenções para discutir com os alunos outras formas e possibilidades de resolução. Apresentar os slides para os alunos é uma possibilidade, mas será muito mais produtivo discutir as soluções apresentadas pelos próprios alunos.
Propósito: Compartilhar diferentes estratégias utilizadas para a solução do problema e conduzir o fechamento das ideias discutidas até o momento.
Discuta com a turma:
- Como você pensou para descobrir a solução deste problema?
- Alguém usou uma estratégia diferente?
Discussão da solução

Tempo sugerido: 10 minutos. (Slides 5, 6 e 7)
Orientação: Os alunos discutiram a solução nas duplas, mas neste momento é importante compartilhar com a turma toda, as diferentes estratégias utilizadas para encontrar a solução, mesmo aquelas que tenham fracassado em algum momento. Neste, e nos próximos slides, apresentamos passo a passo, uma possibilidade, talvez a mais recorrente, mas sugerimos que utilize o guia de intervenções para discutir com os alunos outras formas e possibilidades de resolução. Apresentar os slides para os alunos é uma possibilidade, mas será muito mais produtivo discutir as soluções apresentadas pelos próprios alunos.
Propósito: Compartilhar diferentes estratégias utilizadas para a solução do problema e conduzir o fechamento das ideias discutidas até o momento.
Discuta com a turma:
- Como você pensou para descobrir a solução deste problema?
- Alguém usou uma estratégia diferente?
Discussão da solução
Tempo sugerido: 10 minutos. (Slides 5, 6 e 7)
Orientação: Os alunos discutiram a solução nas duplas, mas neste momento é importante compartilhar com a turma toda, as diferentes estratégias utilizadas para encontrar a solução, mesmo aquelas que tenham fracassado em algum momento. Neste, e nos próximos slides, apresentamos passo a passo, uma possibilidade, talvez a mais recorrente, mas sugerimos que utilize o guia de intervenções para discutir com os alunos outras formas e possibilidades de resolução. Apresentar os slides para os alunos é uma possibilidade, mas será muito mais produtivo discutir as soluções apresentadas pelos próprios alunos.
Propósito: Compartilhar diferentes estratégias utilizadas para a solução do problema e conduzir o fechamento das ideias discutidas até o momento.
Discuta com a turma:
- Como você pensou para descobrir a solução deste problema?
- Alguém usou uma estratégia diferente?
Encerramento

Tempo sugerido: 3 minutos.
Orientação: Projete ou leia o texto do slide para a turma, retomando os objetivos propostos para esta aula.
Propósito: Retomar os objetivos propostos para esta aula.
Raio X

Tempo sugerido: 10 minutos.
Orientação: Peça que, individualmente, os alunos leiam a atividade e a realizem. Quando terminarem, faça a correção coletiva.
Utilize o guia de intervenções para discutir com os alunos as formas e possibilidades de resolução.
Propósito: Resolver problema que envolve a ideia de razão entre as partes e entre as partes e o todo na partilha de uma quantidade em duas partes desiguais.
Materiais complementares para impressão:
Raio X
Resolução do raio x
Atividade complementar
Resolução da atividade complementar
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. 
 Retomada
Retomada