Guia de intervenções
Plano de Aula
Plano de aula: Stop dos divisores
Plano 5 de uma sequência de 7 planos. Veja todos os planos sobre Ampliação dos conceitos de múltiplos e divisores
Por: Luiz Filipe Trovão
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Luiz Filipe Trovão
Mentor: Ferdinando Caíque Genghini Dantas Lobo
Especialista: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF07MA01 - Resolver e elaborar problemas com números naturais, envolvendo as ideias de múltiplos, divisores e divisibilidade.
Objetivos específicos
- Determinar os divisores de números naturais, utilizando fatoração.
Conceito-chave
Cálculo de divisores.
Recursos necessários
Lápis, borracha e caderno;
Jogo impresso: Stop dos divisores.
Habilidades BNCC:
Objetivos de aprendizagem
- Determinar os divisores de números naturais, utilizando fatoração.
Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
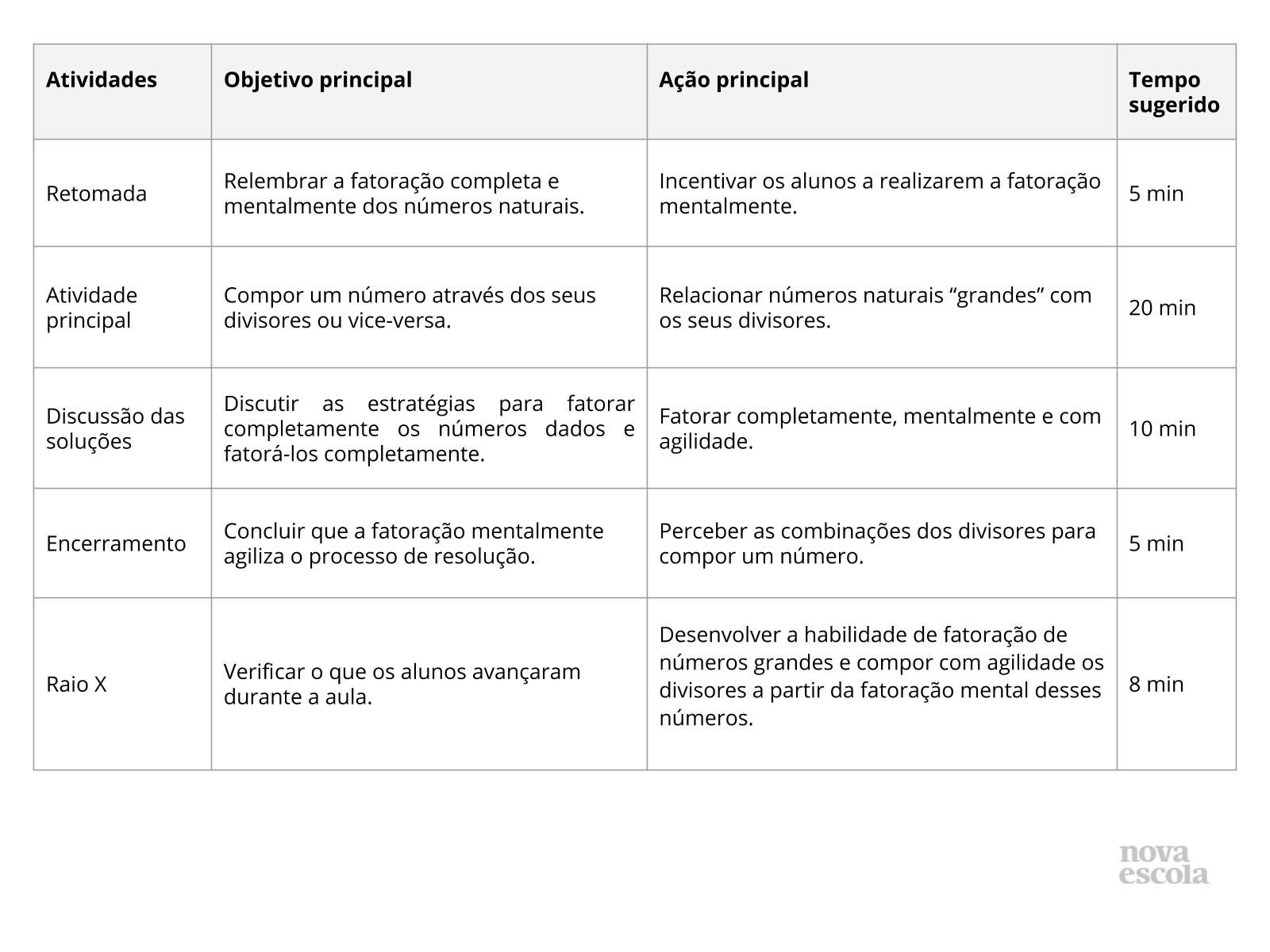
Objetivo
Tempo sugerido: 2 minutos.
Orientação: Projete, escreva no quadro ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Leituras:
Retomada

Tempo sugerido: 5 minutos.
Orientações: Inicie a aula solicitando que os alunos realizem mentalmente a fatoração completa do número 24 registrando no caderno todos os fatores encontrados.
Propósito: Retomar alguns conceitos que serão importantes para o desenvolvimento da atividade.
Discuta com a turma:
- Como podemos escrever o número 24 na forma completamente fatorada?
Dê oportunidade para que vários alunos possam falar suas respostas e como chegaram à fatoração completa do número. Como a proposta é fatorar um número mentalmente, não deve ser usado nenhum processo de algoritmo na fatoração.
Por exemplo, se algum aluno disser que o número 24 fatorado completamente é igual a 3x8, questione a turma se os números 3 e 8 já estão completamente fatorados, pois 3x8 representa uma fatoração do número 24, mas o número 8 não está fatorado completamente. Os alunos precisam compreender que o número 8 é igual a dois elevado ao cubo, ou seja, 8=2x2x2=23.
Nesse momento, professor, é importante que os próprios alunos consigam concluir a forma fatorada do número 24 e que ele é composto pelo 23x3.
- O número 10 é divisor de 24?
Quando o aluno conclui que 24=23x3 e que 10=2x5, ele deve compreender que 24 não é divisível por 10, pois o fator 5 do número 10 não está presente no número 24. Mas, atenção! Esse momento é importante que os alunos discutam e que cheguem a essa conclusão. A intenção aqui não é que os alunos dividam 24 por 10 e vejam que o número não é divisível.
Após essa discussão inicial, peça que os alunos fatorem mentalmente e completamente os números 48 e 240 e que registrem essa forma fatorada no caderno.
- Como podemos escrever o número 48 e 240 na forma completamente fatorada?
Ao escrever os números 48 e 240 na forma completamente fatorada, sugerimos que seja mostrado o caminho:
O aluno pode calcular a fatoração completa do número 48 de várias maneiras, como os exemplos abaixo:
48 = 24x2
= 23x3x2
= 24x3
Ou
48 = 12 x 4
= 22x3x22
=24x3
Ou
48 = 3 x 16
=3x24
E da mesma maneira o número 240. Uma possível estratégia é que 10 é divisor de 240, pois 240=24x10, e como 10=2x5 e 24=23x3, pode-se concluir que 240=24x3x5,
240=24x10=23x3x2x5 = 24x3x5
- O número 10 é divisor de 48 e 240?
O número 10 não é divisor de 48, pois 48=24x3 e como 10=2x5, o fator 5 do número 10 não está presente na fatoração do número 48 e portanto, o número 10 não é divisor de 48.
Como 240=24x10, o número 10 é divisor de 240.
Atividade principal

Tempo sugerido: 20 minutos (slides 4 e 5).
Orientações: Proponha aos alunos o jogo STOP DOS DIVISORES, uma atividade em que os alunos compõem os divisores a partir da fatoração desses números.
Essa atividade deve ser realizada em duplas e cada aluno deverá usar o seu próprio caderno. Atenção ao dividir as duplas, pois elas devem ser equilibradas! Os alunos devem ser agrupados de acordo com o nível de aprendizagem e dificuldade semelhantes, para que eles sintam motivados na “disputa”, uma vez que seus pares têm desenvolvimento semelhante ao dele.
Como o nome do jogo já traz a palavra em inglês STOP, que quer dizer PARE, explique para os alunos que nesse jogo, eles irão calcular os divisores de vários números, um de cada vez, e que, ao comando do professor, eles deverão parar de escrever os divisores sempre que ele disser STOP.
É importante que fique claro para os alunos que eles farão a decomposição em fatores e escreverão o maior número possível de divisores sem utilizar o processo de algoritmo da fatoração.
Entregue para os alunos a tabela impressa, onde serão realizados os registros do jogo, tanto o número apontado quanto dos divisores desse número encontrados pelos alunos.
Nesse momento, fale ou escreva na lousa o número 45. Esse primeiro número servirá para você verificar se todas as duplas compreenderam a atividade. Após um minuto, fale STOP e peça que os alunos verifiquem nas suas duplas quantos divisores foram encontrados e quais são eles, a fim de realizar uma análise entre as semelhanças e diferenças nos valores encontrados.
Após essa primeira análise, peça que algumas duplas compartilhem os seus resultados. Além de compartilhar os resultados, como pensaram e registraram para chegar ao maior número possível de divisores com agilidade.
Assim, é interessante que venha através dos alunos que 45 = 5 x 9 = 5 x 3 x 3, pois combinando os fatores, tem o 3 como divisor, o número 5, o 3x3=9, o 3x5=15, o 3x3x5=45 e o 1 que é divisor de todos os números. Concluindo que os divisores de 45 são os números 1, 3, 5, 9, 15 e 45.
Observe que nem todos os alunos terão encontrado todos os divisores, mas como eles estarão em duplas equilibradas, eles se sentirão motivados para serem os mais rápidos e, assim, desenvolverão os cálculos com agilidade.
Marca ponto o aluno da dupla que tiver escrito o maior números de divisores corretos. Caso eles encontrem o mesmo número de divisores corretos, ambos pontuam naquela rodada. No final de todas as rodadas, o vencedor será o que apresentar o maior somatório de pontos.
Se algum aluno tiver respondido algum número diferente dos divisores do número 45, é interessante que explique para os colegas o seu raciocínio e é importante que ele compreenda o porquê do número não ser divisor. Por exemplo, se a resposta for 7, pergunte aos alunos por que o número 7 não é divisor de 45. Ele precisa entender que o 7 não é uma das “peças” (fatores) que compõem o número 45. E ainda, que 45:7 não é uma divisão exata.
Após todos os alunos entenderem a dinâmica da atividade, entregue a tabela impressa do arquivo da atividade da aula que está representada no slide 4, e diga que aqueles serão os próximos números a serem explorados no jogo (300, 1200 e 2400) peça para que eles analisem um em cada rodada do jogo, e após o tempo de escrita desses divisores é muito importante que toda a turma compartilhe os resultados e aconteça esse momento de socialização.
Professor, caso você queira, sugira outros números para que seja dada uma continuação ao jogo no caderno. Sugestão de números: 3500000, 64000000.
Propósito: Encontrar o maior número possível dos divisores de um número mentalmente.
Discuta com a turma:
- Pergunte aos alunos se eles entenderam as regras apresentadas.
Nesse momento, aproveite para tirar dúvidas e esclarecer possíveis incompreensões. Quando todos tiverem entendido, proponha a atividade para os alunos, lembre-se: um número de cada vez e para cada número o professor deverá estipular um tempo de escrita dos divisores, por exemplo, o número 300 poderá ser de um a dois minutos, os demais o professor poderá aumentar o tempo e ao final desse tempo, dizer STOP.
- Como podemos escrever o número 2400 na forma completamente fatorada?
Peça que eles fatorem o número 2400 mentalmente também. Observe que é um número maior, mas nesse momento o aluno já será capaz de associar o número 2400 com 24x100 e assim, rapidamente, poderá fatorá-lo. Concluindo que 2400=24x100=23x3x22x52=25x3x52.
Nesse momento, professor você pode testar com os alunos outros divisores, por exemplo: 15 é divisor de 2400?
Espera-se que a resposta seja sim, pois 15=3x5 e tanto o 3 como o 5 fazem parte do número 2400.
- O número 21 é divisor de 2400?
Espere o seu aluno analisar e dar a sua resposta, pois você estará apenas conduzindo, fazendo as perguntas, criando oportunidades para o aluno aprender, você não vai dar pronto o raciocínio para o aluno. Assim, ao fatorar o número 21 e concluir que 21=3x7, ele entenderá que 21 não é divisor de 2400, pois o 7 não faz parte do 2400, ou ainda o 7 não é um fatores desse número.
Materiais complementares para impressão:
Resolução da atividade principal
Leituras:
Atividade principal

Tempo sugerido: 20 minutos (slides 4 e 5).
Orientações: Proponha aos alunos o jogo STOP DOS DIVISORES, uma atividade em que os alunos compõem os divisores a partir da fatoração desses números.
Essa atividade deve ser realizada em duplas e cada aluno deverá usar o seu próprio caderno. Atenção ao dividir as duplas, pois elas devem ser equilibradas! Os alunos devem ser agrupados de acordo com o nível de aprendizagem e dificuldade semelhantes, para que eles sintam motivados na “disputa”, uma vez que seus pares têm desenvolvimento semelhante ao dele.
Como o nome do jogo já traz a palavra em inglês STOP, que quer dizer PARE, explique para os alunos que nesse jogo, eles irão calcular os divisores de vários números, um de cada vez, e que, ao comando do professor, eles deverão parar de escrever os divisores sempre que ele disser STOP.
É importante que fique claro para os alunos que eles farão a decomposição em fatores e escreverão o maior número possível de divisores sem utilizar o processo de algoritmo da fatoração.
Entregue para os alunos a tabela impressa, onde serão realizados os registros do jogo, tanto o número apontado quanto dos divisores desse número encontrados pelos alunos.
Nesse momento, fale ou escreva na lousa o número 45. Esse primeiro número servirá para você verificar se todas as duplas compreenderam a atividade. Após um minuto, fale STOP e peça que os alunos verifiquem nas suas duplas quantos divisores foram encontrados e quais são eles, a fim de realizar uma análise entre as semelhanças e diferenças nos valores encontrados.
Após essa primeira análise, peça que algumas duplas compartilhem os seus resultados. Além de compartilhar os resultados, como pensaram e registraram para chegar ao maior número possível de divisores com agilidade.
Assim, é interessante que venha através dos alunos que 45 = 5 x 9 = 5 x 3 x 3, pois combinando os fatores, tem o 3 como divisor, o número 5, o 3x3=9, o 3x5=15, o 3x3x5=45 e o 1 que é divisor de todos os números. Concluindo que os divisores de 45 são os números 1, 3, 5, 9, 15 e 45.
Observe que nem todos os alunos terão encontrado todos os divisores, mas como eles estarão em duplas equilibradas, eles se sentirão motivados para serem os mais rápidos e, assim, desenvolverão os cálculos com agilidade.
Marca ponto o aluno da dupla que tiver escrito o maior números de divisores corretos. Caso eles encontrem o mesmo número de divisores corretos, ambos pontuam naquela rodada. No final de todas as rodadas, o vencedor será o que apresentar o maior somatório de pontos.
Se algum aluno tiver respondido algum número diferente dos divisores do número 45, é interessante que explique para os colegas o seu raciocínio e é importante que ele compreenda o porquê do número não ser divisor. Por exemplo, se a resposta for 7, pergunte aos alunos por que o número 7 não é divisor de 45. Ele precisa entender que o 7 não é uma das “peças” (fatores) que compõem o número 45. E ainda, que 45:7 não é uma divisão exata.
Após todos os alunos entenderem a dinâmica da atividade, entregue a tabela impressa do arquivo da atividade da aula que está representada no slide 4, e diga que aqueles serão os próximos números a serem explorados no jogo (300, 1200 e 2400) peça para que eles analisem um em cada rodada do jogo, e após o tempo de escrita desses divisores é muito importante que toda a turma compartilhe os resultados e aconteça esse momento de socialização.
Professor, caso você queira, sugira outros números para que seja dada uma continuação ao jogo no caderno. Sugestão de números: 3500000, 64000000.
Propósito: Encontrar o maior número possível dos divisores de um número mentalmente.
Discuta com a turma:
- Pergunte aos alunos se eles entenderam as regras apresentadas.
Nesse momento, aproveite para tirar dúvidas e esclarecer possíveis incompreensões. Quando todos tiverem entendido, proponha a atividade para os alunos, lembre-se: um número de cada vez e para cada número o professor deverá estipular um tempo de escrita dos divisores, por exemplo, o número 300 poderá ser de um a dois minutos, os demais o professor poderá aumentar o tempo e ao final desse tempo, dizer STOP.
- Como podemos escrever o número 2400 na forma completamente fatorada?
Peça que eles fatorem o número 2400 mentalmente também. Observe que é um número maior, mas nesse momento o aluno já será capaz de associar o número 2400 com 24x100 e assim, rapidamente, poderá fatorá-lo. Concluindo que 2400=24x100=23x3x22x52=25x3x52.
Nesse momento, professor você pode testar com os alunos outros divisores, por exemplo: 15 é divisor de 2400?
Espera-se que a resposta seja sim, pois 15=3x5 e tanto o 3 como o 5 fazem parte do número 2400.
- O número 21 é divisor de 2400?
Espere o seu aluno analisar e dar a sua resposta, pois você estará apenas conduzindo, fazendo as perguntas, criando oportunidades para o aluno aprender, você não vai dar pronto o raciocínio para o aluno. Assim, ao fatorar o número 21 e concluir que 21=3x7, ele entenderá que 21 não é divisor de 2400, pois o 7 não faz parte do 2400, ou ainda o 7 não é um fatores desse número.
Discussão de soluções

Tempo sugerido: 10 minutos.
Orientações: Quando o professor falar STOP todos os alunos deverão imediatamente parar de escrever os divisores. Nesse momento, o professor pode solicitar que algum aluno escreva a sua resposta na lousa. Após o aluno escrever no quadro, o professor deverá perguntar aos demais, se existe mais algum divisor, se um dos números escritos não é divisor do número apresentado, etc.
Propósito: Apresentar e compartilhar meios utilizados na obtenção da solução, a fim de expor diferentes caminhos para se obter o mesmo resultado.
Discuta com a turma:
- O 21 é divisor de 2400? E de 1200?
- Há algum número que seja divisor de 1200 que não seja divisor de 2400? E o contrário?
Encerramento

Tempo sugerido: 5 minutos.
Orientação: Encerre a atividade retomando com os alunos o conceito de divisor e enfatize com eles como é prático fatorar os números mentalmente. Se desejar, anote a frase em destaque no quadro ou num cartaz para deixar exposto em sala de aula.
Por exemplo, o número 70 fatorado completamente pode ser escrito assim: 2x5x7. Uma vez que o número 70=7x10 e como 10=2x5, o número 70=2x5x7.
Além do número 1 que é divisor de todos os números, os divisores do número 70 são os números 2, 5, 7 tomados os fatores primos um a um e suas combinações, de dois a dois: 10(2x5), 14 (2x7), 35 (5x7) ou em grupo de três: 70 (2x5x7).
D(70) = {1, 2, 5, 7, 10, 14, 35, 70}
Logo, conclui-se que: Os divisores de um número são formados pelas possíveis combinações dos fatores primos de um número como demonstrado no exemplo acima.
Propósito: Realizar a conclusão da aula, refletindo sobre os divisores de um número através de sua representação em fatores primos.
Raio x
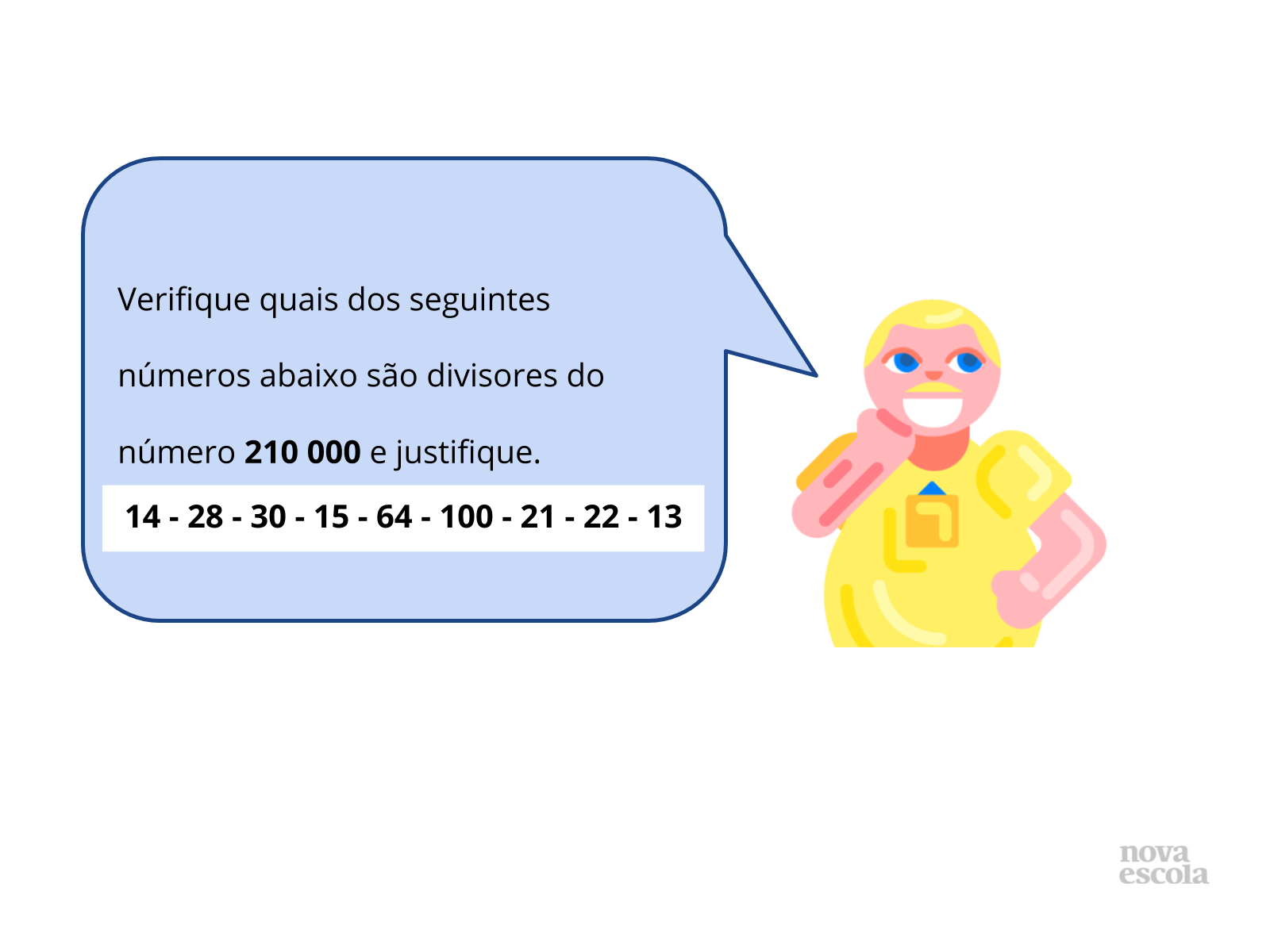
Tempo sugerido: 8 minutos.
Orientações: Apresente o desafio e peça que os alunos o resolvam individualmente e o mais rápido possível. Você pode projetar, passar no quadro ou fazer cópia para os alunos. O raio x é um momento para você avaliar se todos os alunos conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um.
Propósito: Desenvolver a habilidade de fatoração de números grandes e compor com agilidade os divisores a partir da fatoração mental desses números.
Discuta com a turma:
- Como podemos representar de forma fatorada os números múltiplos de 10?
- Como você consegue provar que 14 é divisor de 210 000? E o 28? E o 30?
Materiais complementares para impressão:
Sugestão de adaptação para ensino remoto
Recursos
Necessários:
- Caderno;
- Lápis;
- Régua;
- Grupo de alunos no Whatsapp.
Opcionais:
- Google Sala de Aula.
Para este plano, foque na etapa Atividade Principal.
Atividade principal
A atividade principal consiste em um jogo. Proponha aos alunos o jogo STOP DOS DIVISORES. Nesta atividade,eles resolverão diversas divisões e realizarão comparações.
Combine previamente o jogo com a turma e, usando um Podcast ou o recurso de áudio do Whatsapp, explique as regras e oriente-os a reproduzirem no caderno a tabela para o jogo. No dia marcado, usando o recurso do aplicativo Zoom, divida os alunos em Breakout Rooms (salas para grupos menores dentro da chamada de vídeo), para que possam jogar em duplas.
Para saber mais sobre o Zoom: Pocket-lint (disponível aqui).
Discussão das soluções
A discussão das soluções da atividade é uma etapa importantíssima da aula. Retorne para a sala principal do Zoom e converse com os alunos sobre a atividade. Neste momento, estimule a turma a falar como pensou para resolver o problema.
Convite às famílias
A participação das famílias no processo de aprendizagem é de grande importância para os alunos. Porém, ressaltamos que os pais não são professores de matemática e muitos estão ocupados com outras funções em casa.
Portanto indicamos que sugira aos alunos que, em um momento de descontração, joguem novamente o jogo da atividade principal com as famílias.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Luiz Filipe Trovão
Mentor: Ferdinando Caíque Genghini Dantas Lobo
Especialista: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF07MA01 - Resolver e elaborar problemas com números naturais, envolvendo as ideias de múltiplos, divisores e divisibilidade.
Objetivos específicos
- Determinar os divisores de números naturais, utilizando fatoração.
Conceito-chave
Cálculo de divisores.
Recursos necessários
Lápis, borracha e caderno;
Jogo impresso: Stop dos divisores.