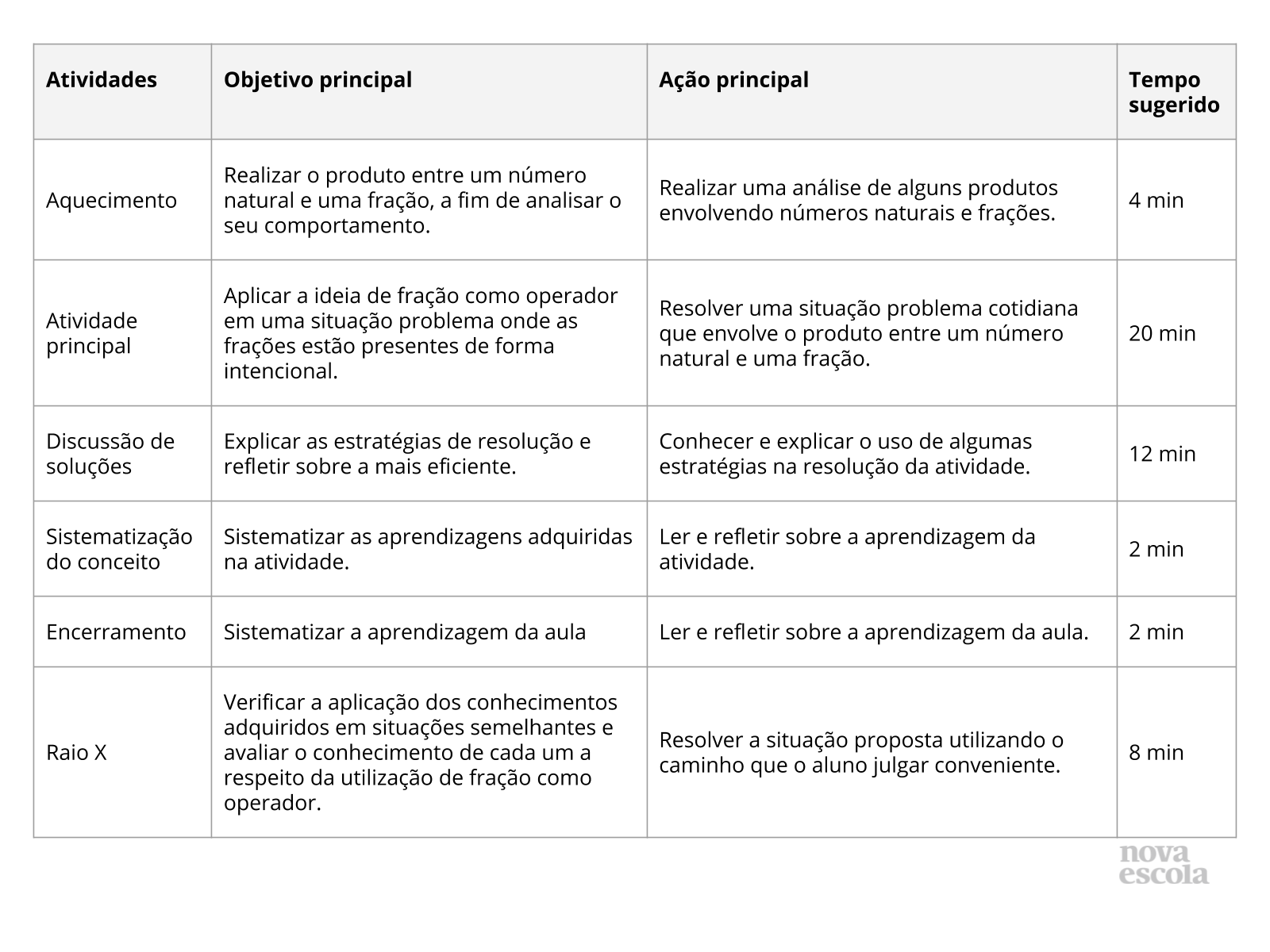
Atividade principal
Plano de Aula
Plano de aula: Fração: um operador a ser considerado
Plano 3 de uma sequência de 5 planos. Veja todos os planos sobre As frações em nosso dia a dia
Por: Luiz Filipe Trovão
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Luiz Filipe Trovão
Mentor: Ferdinando Caíque Genghini Dantas Lobo
Especialista: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF07MA06 - Reconhecer que as resoluções de um grupo de problemas que têm a mesma estrutura podem ser obtidas utilizando os mesmo procedimentos.
EF07MA08 - Comparar e ordenar frações associadas às ideias de partes de inteiros, resultado da divisão, razão e operador.
EF07MA09 - Utilizar, na resolução de problemas, a associação entre razão e fração, como a fração 2/3 para expressar a razão de duas partes de uma grandeza para três partes da mesma ou três partes de outra grandeza.
Objetivos específicos
- Efetuar multiplicações envolvendo uma fração e um número natural;
- Compreender o comportamento do operador multiplicativo, quando ele é uma fração.
Conceito-chave
Multiplicação de uma fração por um número natural; Fração como operador.
Recursos necessários
Lápis, borracha e caderno.
Habilidades BNCC:
Objetivos de aprendizagem
- Efetuar multiplicações envolvendo uma fração e um número natural;
- Compreender o comportamento do operador multiplicativo, quando ele é uma fração.
Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Materiais complementares:
Acesse o arquivo sobre o plano aqui.
Leituras:
- Nova ordem numérica: https://novaescola.org.br/conteudo/2657/nova-ordem-numerica
- Introdução aos números racionais: https://novaescola.org.br/conteudo/2722/introducao-aos-numeros-racionais
- Dividir as dúvidas para compreender as frações: https://novaescola.org.br/conteudo/2135/dividir-as-duvidas-para-compreender-as-fracoes
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma. Caso não seja possível a projeção, escreva o objetivo no quadro.
Propósito: Compartilhar o objetivo da aula.
Aquecimento

Tempo sugerido: 4 minutos (slides 3 e 4)
Orientação: Professor, projete os slides para a sala. Caso não seja possível a projeção, leia as perguntas nos balões de fala e escreva no quadro ou em um cartaz os cálculos realizados no slides 3 e os exercícios propostos no slide 4.
Realize a pergunta presente no balão de fala no slide 3. Ela tem o intuito de verificar o conhecimento que os alunos possuem sobre o produto entre um número natural e uma fração. Espere os alunos apontarem o que lembram sobre o assunto e, em seguida, utilize a demonstração presente no slide, onde os elementos de uma fração são relembrados e um exemplo envolvendo o produto entre um número natural e uma fração é apresentado.
Após a fala sobre o produto entre um número natural e uma fração, diga para os alunos que eles irão praticar esse cálculo. Passe para o slide 4 e dê um tempo para que os alunos executem o que é pedido.
- 8 x 5/4 = 40/4 = 10;
- 5 x 3/2 = 15/2 = 7,5.
Após o tempo dado aos alunos, apresente a resposta e relembre aos alunos que em alguns casos a divisão não será exata. Cabe a eles dar mais um passo e chegar na representação decimal ou deixar na representação fracionária.
Propósito: Realizar o produto entre números naturais e frações de forma conceitual.
Discuta com a turma:
- Há alguma outra forma de resolver o produto entre um número natural e uma fração, diferente do que foi apresentado? Qual?
Aquecimento

Tempo sugerido: 4 minutos (slides 3 e 4)
Orientação: Professor, projete os slides para a sala. Caso não seja possível a projeção, leia as perguntas nos balões de fala e escreva no quadro ou em um cartaz os cálculos realizados no slides 3 e os exercícios propostos no slide 4.
Realize a pergunta presente no balão de fala no slide 3. Ela tem o intuito de verificar o conhecimento que os alunos possuem sobre o produto entre um número natural e uma fração. Espere os alunos apontarem o que lembram sobre o assunto e, em seguida, utilize a demonstração presente no slide, onde os elementos de uma fração são relembrados e um exemplo envolvendo o produto entre um número natural e uma fração é apresentado.
Após a fala sobre o produto entre um número natural e uma fração, diga para os alunos que eles irão praticar esse cálculo. Passe para o slide 4 e dê um tempo para que os alunos executem o que é pedido.
- 8 x 5/4 = 40/4 = 10;
- 5 x 3/2 = 15/2 = 7,5.
Após o tempo dado aos alunos, apresente a resposta e relembre aos alunos que em alguns casos a divisão não será exata. Cabe a eles dar mais um passo e chegar na representação decimal ou deixar na representação fracionária.
Propósito: Realizar o produto entre números naturais e frações de forma conceitual.
Discuta com a turma:
- Há alguma outra forma de resolver o produto entre um número natural e uma fração, diferente do que foi apresentado? Qual?
Atividade principal

Tempo sugerido: 20 minutos (slides 5 e 6)
Orientação: Imprima a atividade principal, entregue para os alunos e leia juntamente com eles a situação apresentada na atividade. Caso não seja possível a projeção, o professor poderá escrever a situação no quadro ou confeccionar um cartaz.
Explique para os alunos que o enunciado da atividade retrata uma situação real, explicando parte do funcionamento da aprovação de uma lei na Câmara dos Deputados.
A utilização dessa situação tem a intenção de tratar de um assunto, onde as frações aparecem naturalmente como operador e faz parte do cotidiano de todos.
Professor, caso deseje se aprofundar um pouco mais no assunto, a seção Materiais Complementares ao final dessas anotações, conta com algumas sugestões de leituras.
Instigue os alunos a pensarem qual é a função da fração nessa atividade, mais precisamente o significado das frações 1/3 e 3/5. Caso necessário, solicite que eles apontem algum exemplo do cotidiano, que se utilizem de frações, a fim de que eles façam uma analogia com algo mais palpável. Após essas ações, disponibilize tempo para que eles resolvam a atividade.
Organize os alunos em duplas para a resolução da atividade. Os itens “a” e “b” trazem problemáticas sobre a situação do enunciado. Acompanhe os alunos na resolução do problema, mas não induza a algum tipo de resolução padrão. Deixe com que os alunos desenvolvam técnicas variadas.
O item “c” tem o intuito de fazer com que o aluno desenvolva um problema a partir do enunciado, utilizando o conceito de frações. Os alunos deverão desenvolver um problema para o colega de dupla resolver. Após a resolução, a troca é desfeita e o aluno corrige a atividade feita pelo seu colega. Este item visa uma maior interação entre a sala, então é importante que você, professor, acompanhe os alunos circulando pela sala.
Propósito: Utilizar uma fração como fator multiplicativo em uma situação cotidiana.
Discuta com a turma:
- O que as frações 1/3 e 3/5 representam nessa atividade?
- Como podemos calcular 1/3 de um certo valor?
- Se conhecemos 3/5 de uma certa quantia, como podemos descobrir o total dessa quantia?
Materiais complementares:
Atividade principal

Tempo sugerido: 20 minutos (slides 5 e 6)
Orientação: Imprima a atividade principal, entregue para os alunos e leia juntamente com eles a situação apresentada na atividade. Caso não seja possível a projeção, o professor poderá escrever a situação no quadro ou confeccionar um cartaz.
Explique para os alunos que o enunciado da atividade retrata uma situação real, explicando parte do funcionamento da aprovação de uma lei na Câmara dos Deputados.
A utilização dessa situação tem a intenção de tratar de um assunto, onde as frações aparecem naturalmente como operador e faz parte do cotidiano de todos.
Professor, caso deseje se aprofundar um pouco mais no assunto, a seção Materiais Complementares ao final dessas anotações, conta com algumas sugestões de leituras.
Instigue os alunos a pensarem qual é a função da fração nessa atividade, mais precisamente o significado das frações 1/3 e 3/5. Caso necessário, solicite que eles apontem algum exemplo do cotidiano, que se utilizem de frações, a fim de que eles façam uma analogia com algo mais palpável. Após essas ações, disponibilize tempo para que eles resolvam a atividade.
Organize os alunos em duplas para a resolução da atividade. Os itens “a” e “b” trazem problemáticas sobre a situação do enunciado. Acompanhe os alunos na resolução do problema, mas não induza a algum tipo de resolução padrão. Deixe com que os alunos desenvolvam técnicas variadas.
O item “c” tem o intuito de fazer com que o aluno desenvolva um problema a partir do enunciado, utilizando o conceito de frações. Os alunos deverão desenvolver um problema para o colega de dupla resolver. Após a resolução, a troca é desfeita e o aluno corrige a atividade feita pelo seu colega. Este item visa uma maior interação entre a sala, então é importante que você, professor, acompanhe os alunos circulando pela sala.
Propósito: Utilizar uma fração como fator multiplicativo em uma situação cotidiana.
Discuta com a turma:
- O que as frações 1/3 e 3/5 representam nessa atividade?
- Como podemos calcular 1/3 de um certo valor?
- Se conhecemos 3/5 de uma certa quantia, como podemos descobrir o total dessa quantia?
Discussão da solução

Tempo sugerido: 12 minutos (slides 7 ao 9)
Orientação: Inicialmente, peça para que os alunos discutam as soluções dos itens “a” e “b” em duplas, sempre acompanhando-os em seus raciocínios. Solicite que as dupla compartilhem entre si o problema elaborado no item “c”, de modo que um resolva a atividade do outro.
Em seguida, peça para que alguns alunos exponham a resolução dos itens “a” e “b” e o problema que criaram no item “c” juntamente com a resposta apresentada pelo colega. A ideia não é direcionar para que determinado aluno apresente a solução, porém quanto mais caminhos diferentes forem apresentados para se chegar na mesma resposta, mais rica será a discussão.
Após os alunos compartilharem as estratégias utilizadas na resolução dos exercícios, passe para essa série de slides. Caso não seja possível a projeção, o professor deverá reproduzir, pelo menos, os cálculos realizados para se chegar aos valores solicitados, no quadro ou em um cartaz, o restante da solução pode ser lida para a sala.
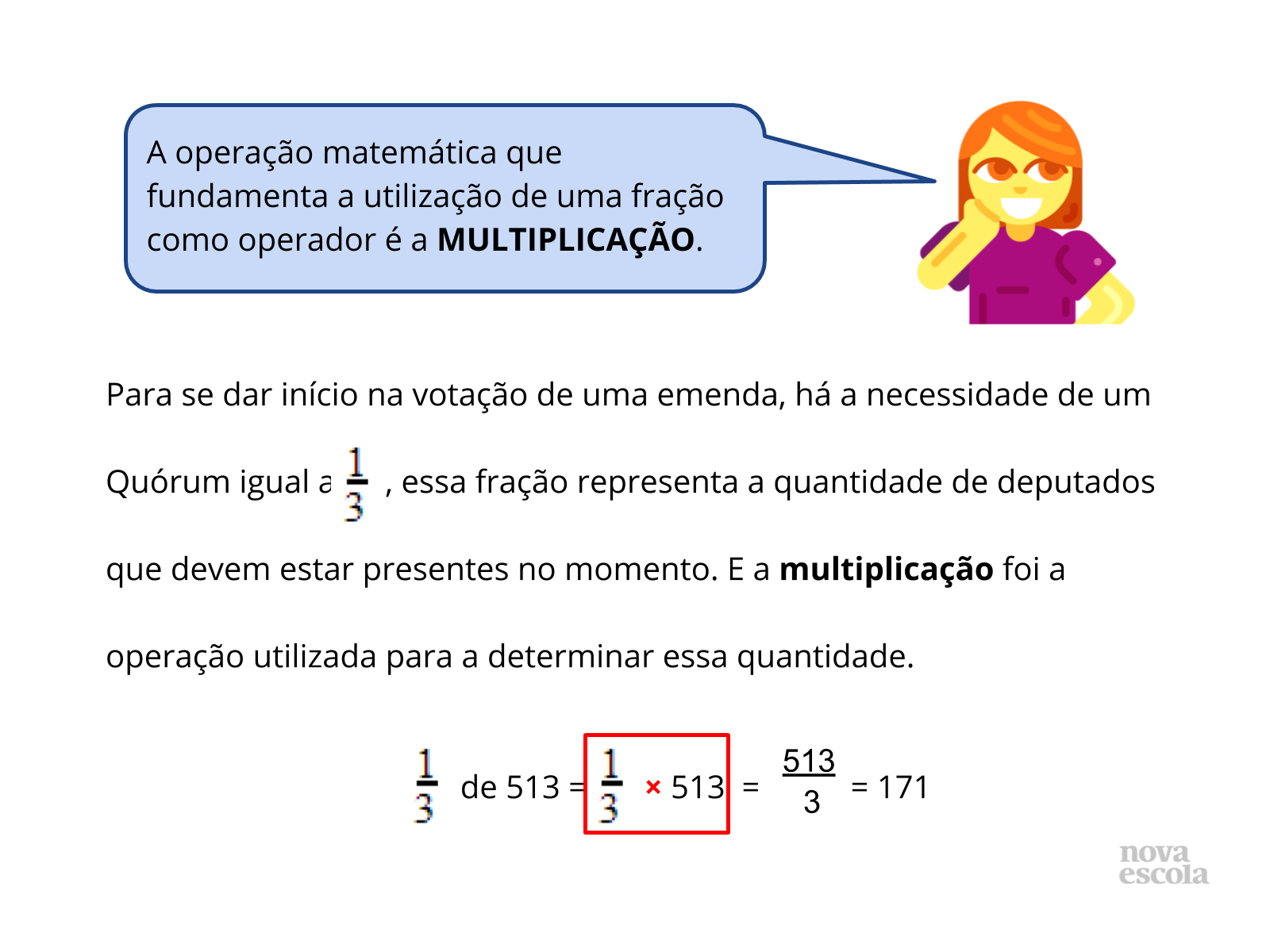
Essa resolução aponta para utilização de uma fração como operador como solução do item “a” (slide 7) ao multiplicar o total de deputados (513), pela fração que representa o Quórum (1/3).
É interessante notar que o exercício aponta para uma resposta negativa, pois mesmo tendo comparecido 170 deputados, é necessário que 171 comparecimentos para que a votação ocorresse .
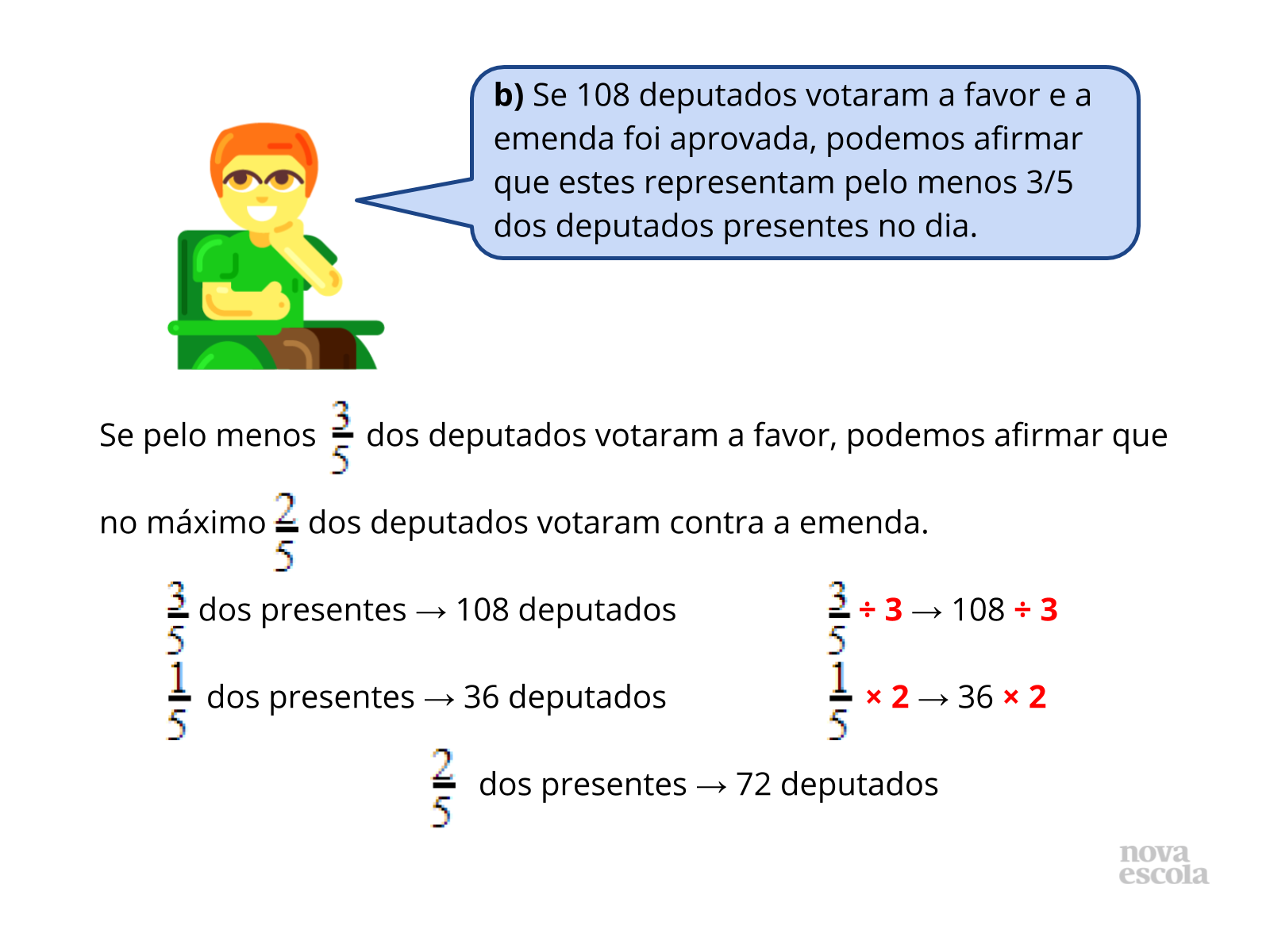
O item “b” (slides 8 e 9) se utiliza inicialmente de uma decomposição, ou uma divisão de uma fração por um número natural, pois ao saber que 3/5 = 108 deputados (3 partes de 5 representam 108 deputados), chegamos à conclusão por meio desses cálculos que 1 parte de 5 representa 36 deputados, ou seja, 1/5 = 36 deputados.
Como 2/5 dos presentes votaram contra, realizando o produto entre 2 e 1/5 (2 e 36), concluímos que 2/5 = 72 deputados, ou seja, 2 partes de 5 representam 72 deputados.
Ao possuir 108 que já votaram a favor e tendo calculado 72 que votaram contra, é possível afirmar que no dia da votação estavam presentes pelo menos 180 deputados (slide 9).
O item “c”, por ser aberto, caberá ao professor interpretar alguns dos problemas que forem apresentados pelos alunos.
Propósito: Apresentar e compartilhar meios utilizados na obtenção da solução, a fim de expor diferentes caminhos para se obter o mesmo resultado.
Discuta com a turma:
- De acordo com o exercício, é possível que a fração que representa a quantidade de deputados que votaram contra seja maior que os 3/5 que votaram a favor?
Discussão da solução
Tempo sugerido: 12 minutos (slides 7 ao 9)
Orientação: Inicialmente, peça para que os alunos discutam as soluções dos itens “a” e “b” em duplas, sempre acompanhando-os em seus raciocínios. Solicite que as dupla compartilhem entre si o problema elaborado no item “c”, de modo que um resolva a atividade do outro.
Em seguida, peça para que alguns alunos exponham a resolução dos itens “a” e “b” e o problema que criaram no item “c” juntamente com a resposta apresentada pelo colega. A ideia não é direcionar para que determinado aluno apresente a solução, porém quanto mais caminhos diferentes forem apresentados para se chegar na mesma resposta, mais rica será a discussão.
Após os alunos compartilharem as estratégias utilizadas na resolução dos exercícios, passe para essa série de slides. Caso não seja possível a projeção, o professor deverá reproduzir, pelo menos, os cálculos realizados para se chegar aos valores solicitados, no quadro ou em um cartaz, o restante da solução pode ser lida para a sala.
Essa resolução aponta para utilização de uma fração como operador como solução do item “a” (slide 7) ao multiplicar o total de deputados (513), pela fração que representa o Quórum (1/3).
É interessante notar que o exercício aponta para uma resposta negativa, pois mesmo tendo comparecido 170 deputados, é necessário que 171 comparecimentos para que a votação ocorresse .
O item “b” (slides 8 e 9) se utiliza inicialmente de uma decomposição, ou uma divisão de uma fração por um número natural, pois ao saber que 3/5 = 108 deputados (3 partes de 5 representam 108 deputados), chegamos à conclusão por meio desses cálculos que 1 parte de 5 representa 36 deputados, ou seja, 1/5 = 36 deputados.
Como 2/5 dos presentes votaram contra, realizando o produto entre 2 e 1/5 (2 e 36), concluímos que 2/5 = 72 deputados, ou seja, 2 partes de 5 representam 72 deputados.
Ao possuir 108 que já votaram a favor e tendo calculado 72 que votaram contra, é possível afirmar que no dia da votação estavam presentes pelo menos 180 deputados (slide 9).
O item “c”, por ser aberto, caberá ao professor interpretar alguns dos problemas que forem apresentados pelos alunos.
Propósito: Apresentar e compartilhar meios utilizados na obtenção da solução, a fim de expor diferentes caminhos para se obter o mesmo resultado.
Discuta com a turma:
- De acordo com o exercício, é possível que a fração que representa a quantidade de deputados que votaram contra seja maior que os 3/5 que votaram a favor?
Discussão da solução

Tempo sugerido: 12 minutos (slides 7 ao 9)
Orientação: Inicialmente, peça para que os alunos discutam as soluções dos itens “a” e “b” em duplas, sempre acompanhando-os em seus raciocínios. Solicite que as dupla compartilhem entre si o problema elaborado no item “c”, de modo que um resolva a atividade do outro.
Em seguida, peça para que alguns alunos exponham a resolução dos itens “a” e “b” e o problema que criaram no item “c” juntamente com a resposta apresentada pelo colega. A ideia não é direcionar para que determinado aluno apresente a solução, porém quanto mais caminhos diferentes forem apresentados para se chegar na mesma resposta, mais rica será a discussão.
Após os alunos compartilharem as estratégias utilizadas na resolução dos exercícios, passe para essa série de slides. Caso não seja possível a projeção, o professor deverá reproduzir, pelo menos, os cálculos realizados para se chegar aos valores solicitados, no quadro ou em um cartaz, o restante da solução pode ser lida para a sala.
Essa resolução aponta para utilização de uma fração como operador como solução do item “a” (slide 7) ao multiplicar o total de deputados (513), pela fração que representa o Quórum (1/3).
É interessante notar que o exercício aponta para uma resposta negativa, pois mesmo tendo comparecido 170 deputados, é necessário que 171 comparecimentos para que a votação ocorresse .
O item “b” (slides 8 e 9) se utiliza inicialmente de uma decomposição, ou uma divisão de uma fração por um número natural, pois ao saber que 3/5 = 108 deputados (3 partes de 5 representam 108 deputados), chegamos à conclusão por meio desses cálculos que 1 parte de 5 representa 36 deputados, ou seja, 1/5 = 36 deputados.
Como 2/5 dos presentes votaram contra, realizando o produto entre 2 e 1/5 (2 e 36), concluímos que 2/5 = 72 deputados, ou seja, 2 partes de 5 representam 72 deputados.
Ao possuir 108 que já votaram a favor e tendo calculado 72 que votaram contra, é possível afirmar que no dia da votação estavam presentes pelo menos 180 deputados (slide 9).
O item “c”, por ser aberto, caberá ao professor interpretar alguns dos problemas que forem apresentados pelos alunos.
Propósito: Apresentar e compartilhar meios utilizados na obtenção da solução, a fim de expor diferentes caminhos para se obter o mesmo resultado.
Discuta com a turma:
- De acordo com o exercício, é possível que a fração que representa a quantidade de deputados que votaram contra seja maior que os 3/5 que votaram a favor?
Sistematização do conceito
Tempo sugerido: 2 minutos
Orientação: Projete o slide e leia para os alunos a conclusão da atividade presente no balão de fala. Caso não seja possível a projeção, copie o texto no quadro, ou em um cartaz ou apenas leia o texto para sala.
Aponte para os alunos que a utilização de frações, do mesmo modo que o efetuado na atividade proposta são chamadas de operador (ou operador multiplicativo), por isso a operação matemática envolvida nesses cálculos é a multiplicação.
Retome o item “a” da atividade realizada realizando a leitura do texto neste slide, concluindo sobre a utilização de frações como operador.
Propósito: Realizar a conclusão sobre o exercício proposto, refletindo sobre a utilização de uma fração como operador.
Discuta com a turma:
- Vocês saberiam apontar mais algum exemplo que utiliza frações como operador?
Encerramento

Tempo sugerido: 2 minutos
Orientação: Projete o slide e leia para os alunos a conclusão da aula. Caso não seja possível a projeção, copie o texto no quadro, ou em um cartaz realizando a leitura apenas do balão de fala presente no slide.
Nesse momento de encerramento da aula, são indicados mais alguns exemplos de utilização de frações no mesmo âmbito que o da atividade principal, aponte esses exemplos para alunos, explicando as frações presentes no mesmo, que representam o Quórum de aprovação de algumas leis específicas na Câmara.
Propósito: Realizar a conclusão sobre o exercício proposto, refletindo sobre a utilização de outras frações em uma situação cotidiana.
Raio X
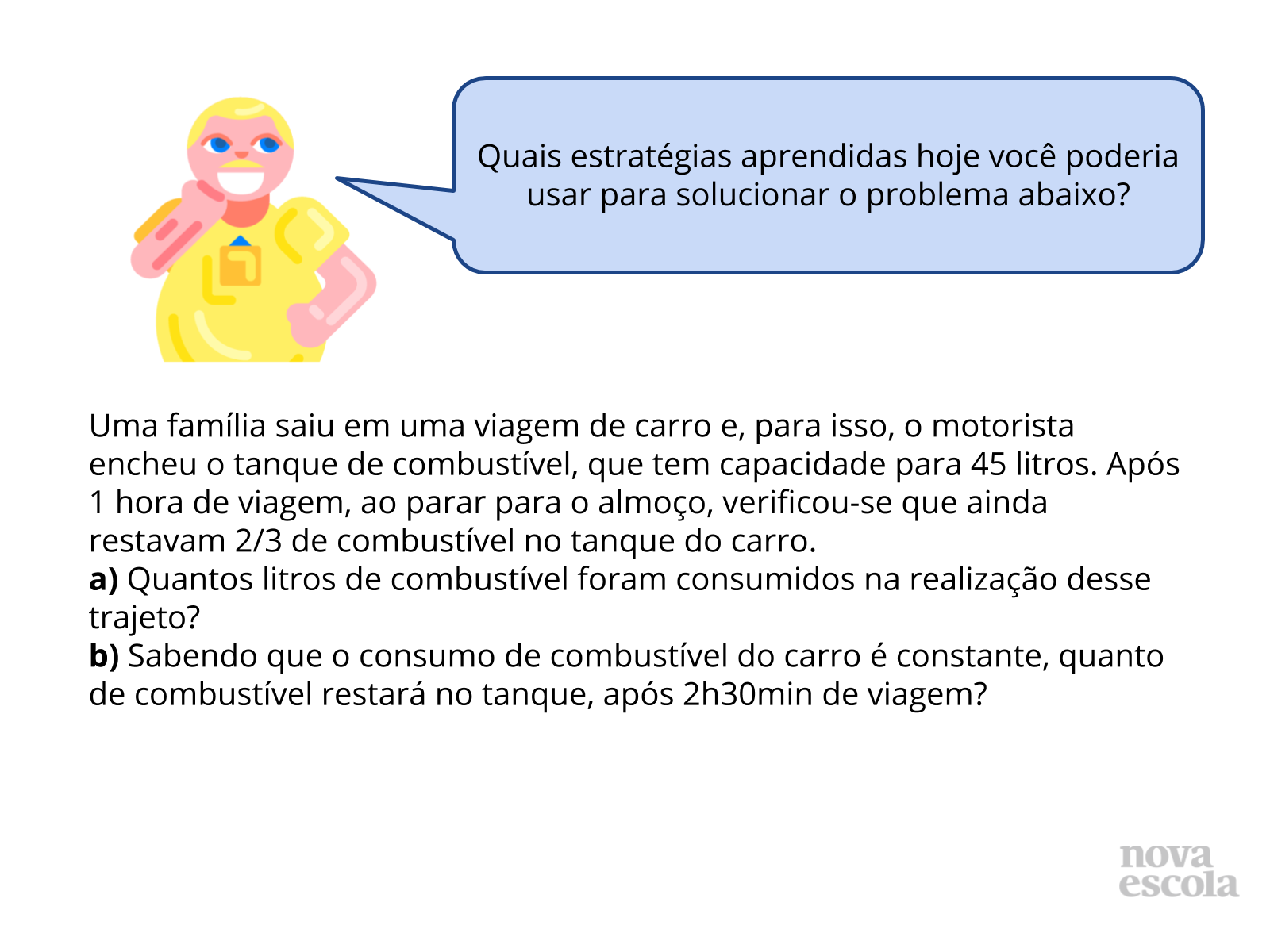
Tempo sugerido: 8 minutos.
Orientação: Apresente a nova situação e peça para que os alunos analisem e resolvam, em um primeiro momento individualmente e em seguida compartilhando a forma de pensar com o colega ao lado. Você pode projetar, passar no quadro ou fazer o download desta atividade e entregar para os seus alunos. O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure anotar e identificar todos os comentários que surgirem.
Propósito: Realizar uma atividade teórica relativa aos conteúdos ensinados na aula.
Discuta com a turma:
- A quantidade de combustível consumida na realização do trajeto foi maior ou menor do que a metade do tanque?
- O que a frase “consumo de combustível do carro é constante” significa no contexto do exercício?
Materiais complementares:
Para os alunos
Para o professor
Sugestão de adaptação para ensino remoto
Código do plano
MAT7_06NUM03
Recursos
- Necessários:
- caderno
- lápis
- régua
- grupo de alunos no WhatsApp
- Opcionais:
- Google Sala de Aula
- vídeo: “Multiplicação de frações e números naturais”, disponível no Khan Academy https://youtu.be/Oei0dcQRHUY, acesso em 17 de jun 2020.
Para este plano, foque na etapa: Aquecimento
Aquecimento
A atividade é uma retomada de conceitos que são fundamentais para a aula. Você pode propor em um movimento de Ensino Híbrido que os alunos assistam ao vídeo “Multiplicação de frações e números naturais”, disponível no Khan Academy, para a retomado dos objetos de conhecimentos. Fotografe e envie via WhatsApp ou e-mail o problema proposto para resolução. Oriente-os que é um momento de retomada de conteúdos e que caso tenham dúvidas, estas serão trabalhadas no decorrer da aula.
Atividade principal
Para a realização da atividade principal os alunos precisam ter acesso ao problema proposto. Para isso, fotografe a atividade principal e disponibilize a imagem no grupo de WhatsApp para que os alunos possam pensar sobre ele. Peça que tentem resolver a atividade. Oriente-os a filmar ou fotografar as suas estratégias e respostas para compartilhar com o professor e a turma no momento da discussão das soluções.
Discussão das soluções
Para uma aula síncrona, você poderá realizar a discussão das soluções imediatamente após a resolução pelos alunos. Analise as soluções enviadas pelos alunos e se possível, compartilhe algumas pelo meio de comunicação estabelecido por vocês. Nesse momento questione os alunos se, de acordo com o exercício, é possível que a fração que representa a quantidade de deputados que votaram contra seja maior que os 3/5 que votaram a favor.
Estimule a turma a perceber que, para conhecer uma solução, podemos seguir por diversos caminhos, e que o erro é uma importante ferramenta para o ensino-aprendizagem, combatendo a valorização excessiva da resposta certa.
Convite às famílias
A participação das famílias no processo de aprendizagem é de grande importância para o aluno. Porém, ressaltamos que os pais não são professores de matemática e muitos estão ocupados com outras funções em casa. Portanto, indicamos a participação das famílias no compartilhamento e discussão de possíveis soluções para os problemas propostos.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Luiz Filipe Trovão
Mentor: Ferdinando Caíque Genghini Dantas Lobo
Especialista: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF07MA06 - Reconhecer que as resoluções de um grupo de problemas que têm a mesma estrutura podem ser obtidas utilizando os mesmo procedimentos.
EF07MA08 - Comparar e ordenar frações associadas às ideias de partes de inteiros, resultado da divisão, razão e operador.
EF07MA09 - Utilizar, na resolução de problemas, a associação entre razão e fração, como a fração 2/3 para expressar a razão de duas partes de uma grandeza para três partes da mesma ou três partes de outra grandeza.
Objetivos específicos
- Efetuar multiplicações envolvendo uma fração e um número natural;
- Compreender o comportamento do operador multiplicativo, quando ele é uma fração.
Conceito-chave
Multiplicação de uma fração por um número natural; Fração como operador.
Recursos necessários
Lápis, borracha e caderno.









