Resumo da aula
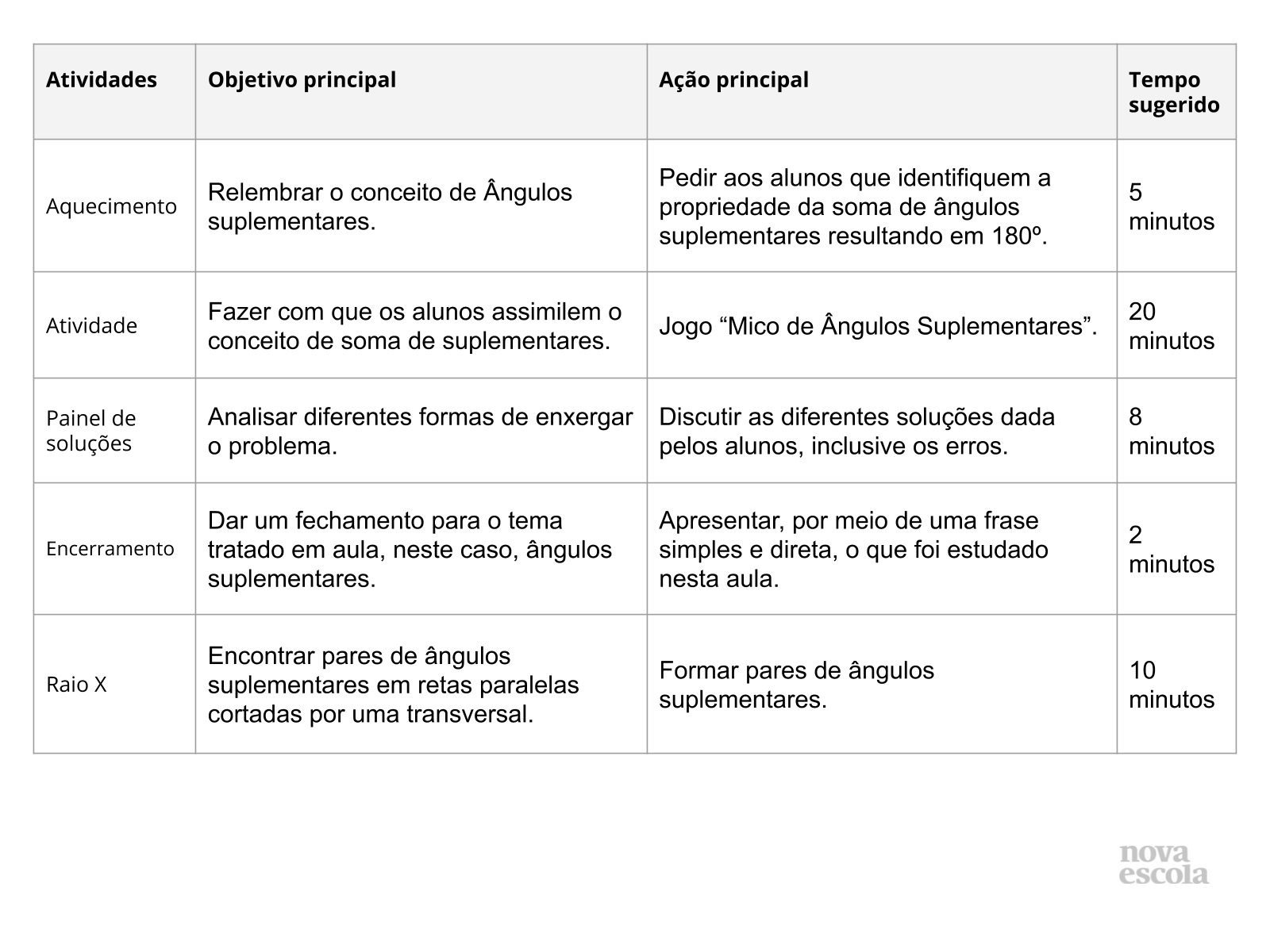
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos
Orientação: Você pode mostrar o slide, ler o objetivo ou escrevê-lo na lousa.
Propósito: Deixar o aluno em prontidão para a aula.
Retomando ângulos suplementares
Tempo sugerido: 5 minutos
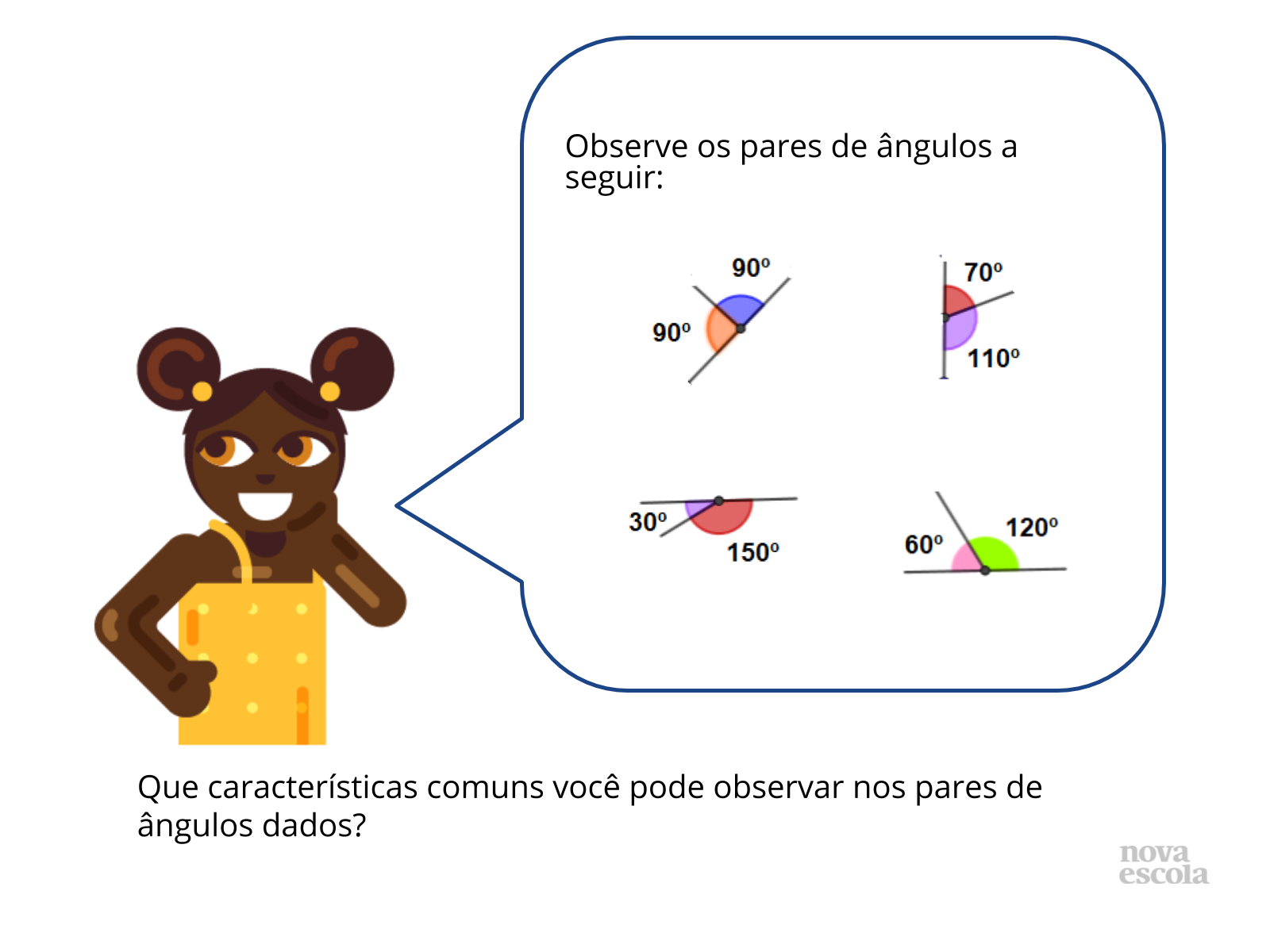
Orientação: Essa atividade pode ser feita em duplas. Diga aos alunos que observem os ângulos e falem tudo o que podem observar que seja comum a todos os pares.
Propósito: Fazer com que o aluno relembre o conceito de ângulos suplementares.
Discuta com a turma:
- Vocês se lembram do que é um ângulo?
- Se eu juntar esses dois ângulos, o que acontece?
- Qual a medida do ângulo que representa uma volta completa?
Resolução: A soma de todos os pares de ângulos sempre resulta em 180º. São pares de ângulos suplementares.
Atividade principal

Tempo sugerido: 20 minutos (Tempo total: slides 4 e 5)
Orientação: O jogo começa retirando-se uma carta do monte e deixando-a de lado. Nenhum dos jogadores pode ver o ângulo contido nela. Isso fará com que uma das cartas fique sem par. Essa carta será o Mico. Depois disso, distribuem-se as demais cartas entre os jogadores. Cada jogador retira todos os pares de ângulos suplementares que possui. Em seguida, escolhe-se um jogador para começar e, no sentido anti-horário retira uma carta do outro jogador. Se esta carta for um ângulo suplementar de alguma carta do jogador que a tirou, ele descarta o par. Caso contrário, o jogador deve juntar a carta tirada às demais e o jogo continua. Perde o jogador que ficar com a carta sem par (O mico). As cartas estão na atividade principal para impressão.
Os alunos podem continuar em duplas para fazer a atividade. Pergunte sobre o que eles aprenderam com o jogo. A soma de dois ângulos suplementares sempre resulta em 180º. Como é o ângulo de 180º? Pergunte se os ângulos precisam ser adjacentes para você saber que juntos formariam um ângulo raso.
Propósito: Aprimorar o conceito de ângulos suplementares através de uma atividade em que seu uso é exigido a todo momento. Localizar ângulos suplementares em um feixe de paralelas cortadas por uma transversal. Verificar que o ângulo raso pode representar ângulos suplementares adjacentes.
Materiais complementares:
Atividade principal
Resolução atividade principal
Guia de intervenção
Jogo do Mico
Tempo sugerido: 20 minutos (Tempo total: slides 4 e 5)
Orientação: O jogo começa retirando-se uma carta do monte e deixando-a de lado. Nenhum dos jogadores pode ver o ângulo contido nela. Isso fará com que uma das cartas fique sem par. Essa carta será o Mico. Depois disso, distribuem-se as demais cartas entre os jogadores. Cada jogador retira todos os pares de ângulos suplementares que possui. Em seguida, escolhe-se um jogador para começar e, no sentido anti-horário retira uma carta do outro jogador. Se esta carta for um ângulo suplementar de alguma carta do jogador que a tirou, ele descarta o par. Caso contrário, o jogador deve juntar a carta tirada às demais e o jogo continua. Perde o jogador que ficar com a carta sem par (O mico). As cartas estão na atividade principal para impressão.
Os alunos podem continuar em duplas para fazer a atividade. Pergunte sobre o que eles aprenderam com o jogo. A soma de dois ângulos suplementares sempre resulta em 180º. Como é o ângulo de 180º? Pergunte se os ângulos precisam ser adjacentes para você saber que juntos formariam um ângulo raso.
Propósito: Aprimorar o conceito de ângulos suplementares através de uma atividade em que seu uso é exigido a todo momento. Localizar ângulos suplementares em um feixe de paralelas cortadas por uma transversal. Verificar que o ângulo raso pode representar ângulos suplementares adjacentes.
Soluções
Tempo sugerido: 8 minutos.
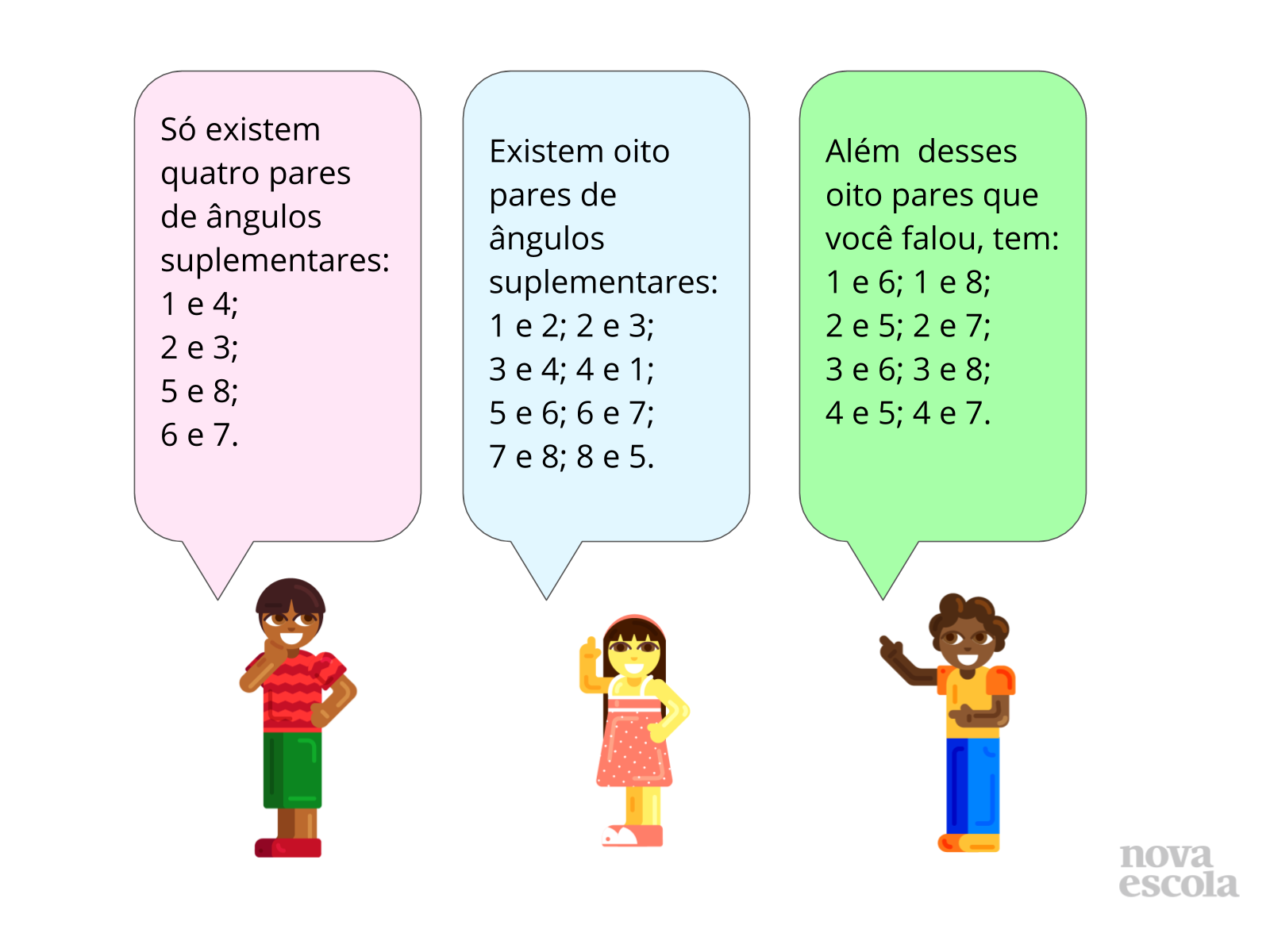
Orientação: Neste momento você vai apresentar e discutir as soluções que apareceram Dê preferência para a solução dos alunos. Procure soluções incorretas e soluções diferentes. No painel acima temos três exemplos de soluções:
Balão rosa: Essa solução pressupõe que os ângulos suplementares são apenas os adjacentes laterais. É uma solução comum porque esses ângulos são os de identificação imediata;
Balão azul: Essa solução é mais completa que a anterior. O aluno também pressupõe que somente os ângulos adjacentes são suplementares, mas ele considera todos os adjacentes e não apenas os laterais;
Balão verde: Essa solução é a mais completa porque considera todos os adjacentes e os não adjacentes.
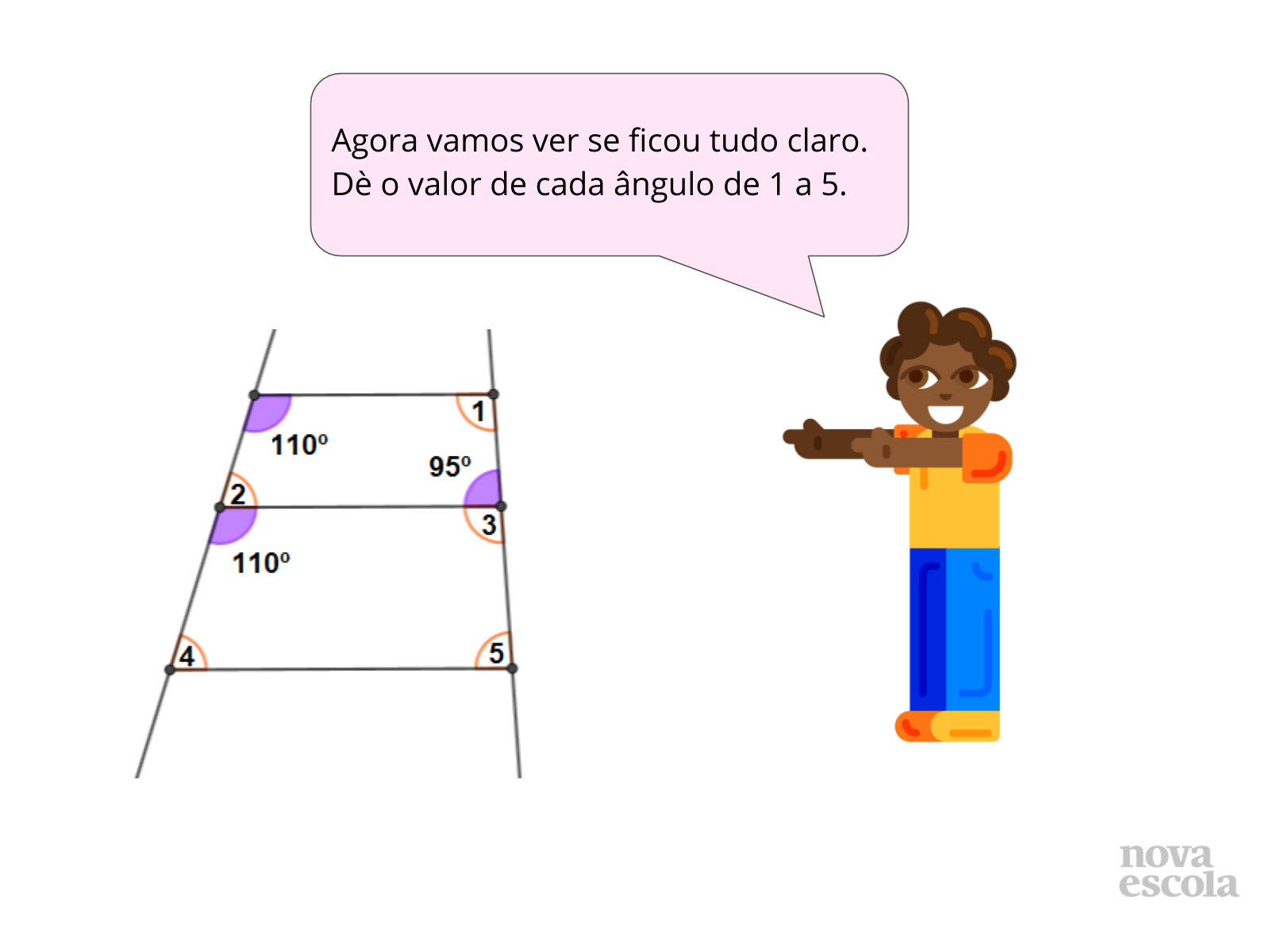
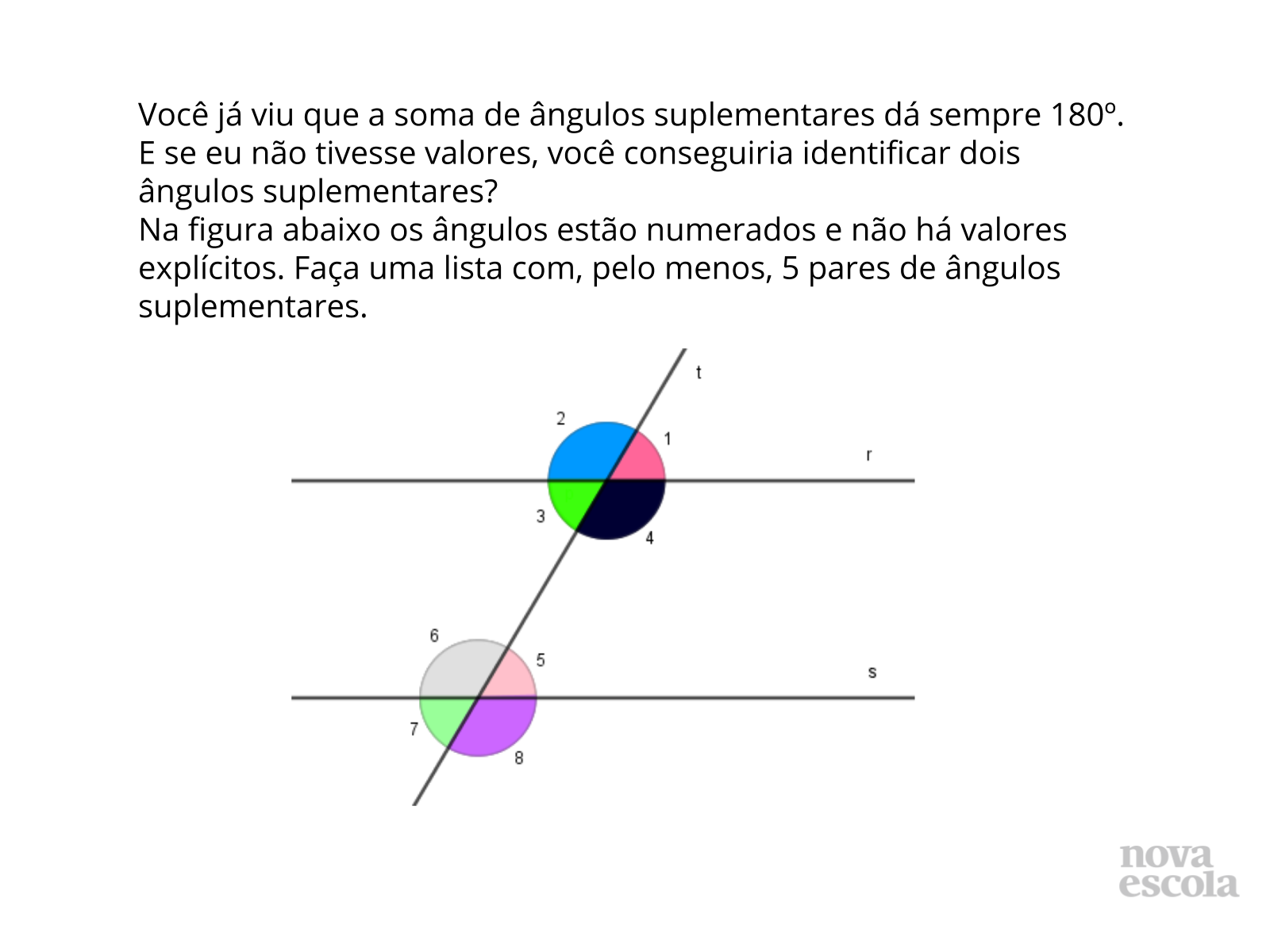
Como a atividade pede 5 pares de ângulos suplementares, é provável que não apareçam todas as dificuldades acima. Provavelmente, apenas a primeira. Mas é importante que eles identifiquem ângulos suplementares que não sejam adjacentes. Caso essa questão não surja espontaneamente, pergunte, por exemplo: “E os ângulos 1 e 6? São suplementares?”; “Qual a definição de ângulos suplementares?”; “Na definição, diz-se que os ângulos devem ser adjacentes?”.
Propósito: Apontar diferentes formas de interpretar e resolver problemas matemáticos. Discutir erros e suas causas.
Fechamento

Tempo sugerido: 2 minutos.
Orientação: Apresente o slide, leia o texto ou passe na lousa.
Propósito: Dar um fechamento ao conteúdo estudado na aula através de uma frase simples, sem muito aprofundamento.
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.