Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Para acessar documento com sugestões de Referências Bibliográficas, clique aqui.
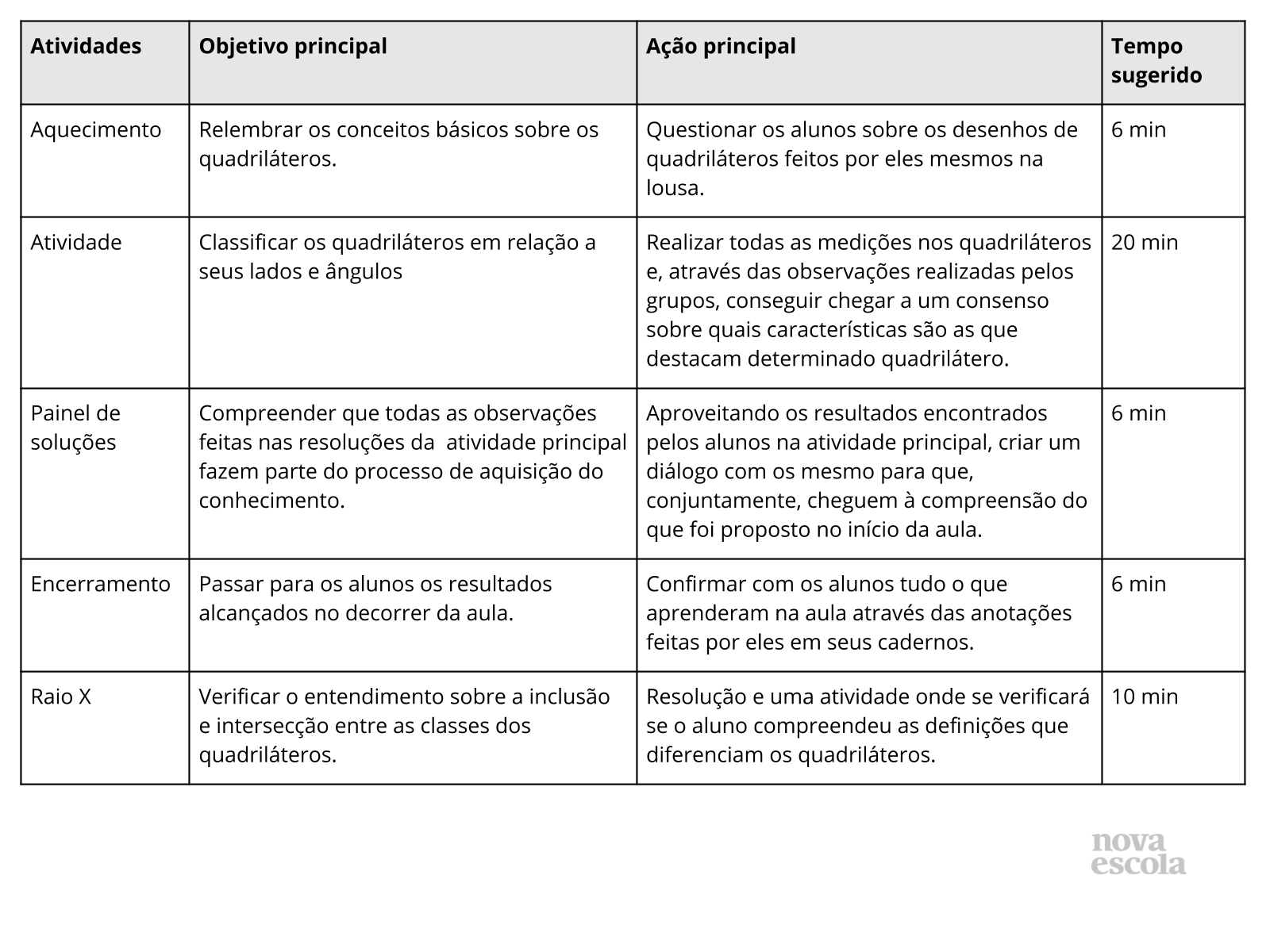
Aquecimento

Tempo sugerido: 6 minutos
Orientações: Peça a alguns alunos para desenharem quadriláteros na lousa. Se nenhum aluno fizer o desenho de um quadrilátero côncavo, faça ao menos um. Converse com os alunos sobre as diferenças entre os quadriláteros desenhados (exemplos de possíveis desenhos feitos pelos alunos aqui). Faça os seguintes questionamentos:
- Todos esses quadriláteros possuem as mesmas características? para conseguirem diferenciar o grupo dos quadriláteros convexos dos côncavos.
- Quantas diagonais um quadrilátero pode ter?
- Elas sempre se cruzam no mesmo lugar? Dividem o quadrilátero em triângulos iguais?
- Conseguem nomear um quadrilátero baseados apenas nas suas principais características?
Propósito: Relembrar as definições básicas dos quadriláteros para um aprofundamento do tema.
Materiais complementares:
Atividade aquecimento
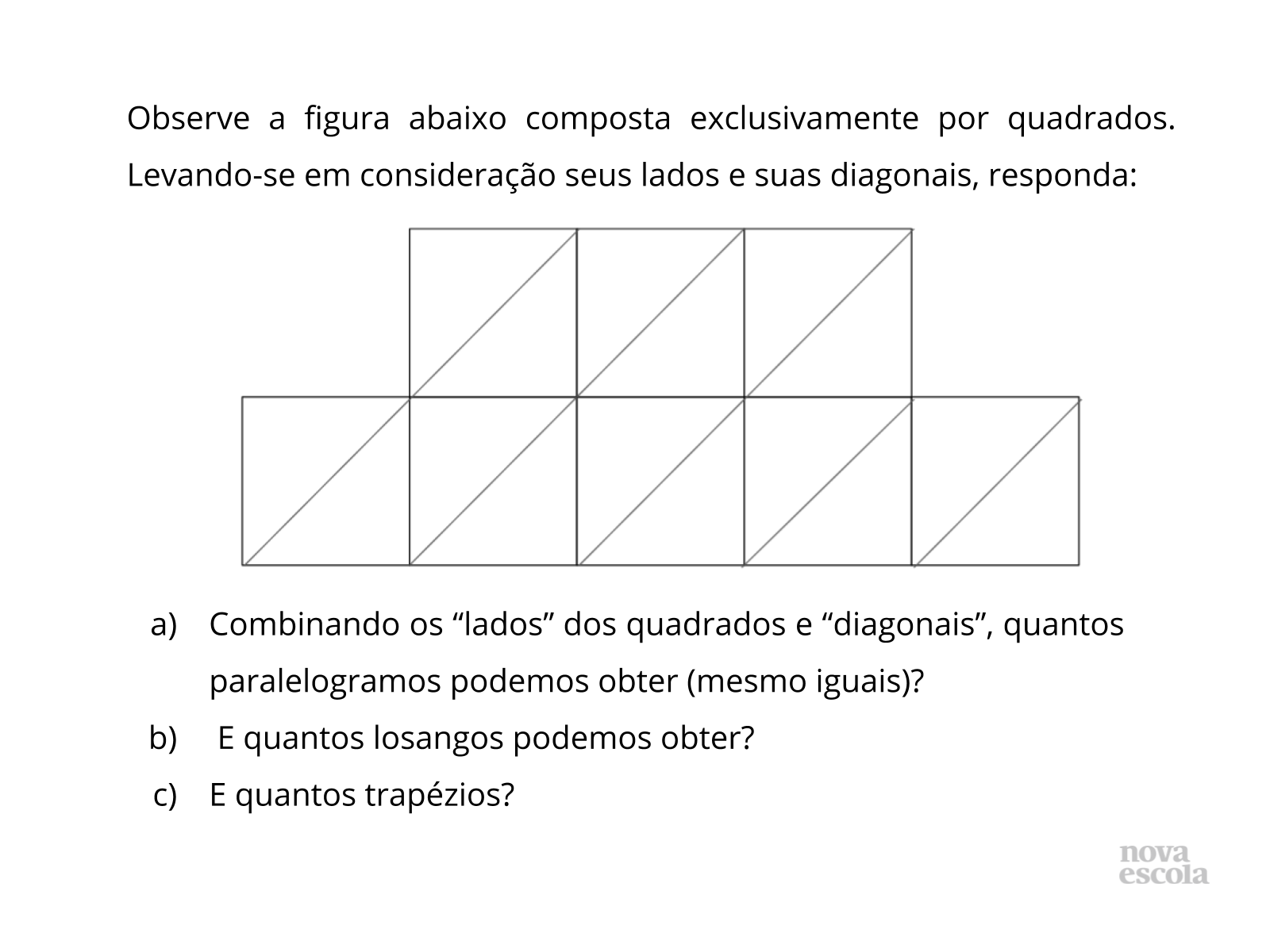
Atividade principal
Tempo sugerido: 20 minutos
Orientações: Divida a classe em grupos, peça que juntem as carteiras, distribua as réguas e os transferidores e as folhas com os quadriláteros impressos (aqui). Diga aos alunos que devem traçar as diagonais e fazer “todas” as medidas necessárias: dos lados, das diagonais e dos ângulos formados dos quadriláteros, incluindo os ângulos do cruzamento das diagonais (que serão os mais importantes) para encontrar as semelhanças. Explique a importância da atenção aos detalhes e que a participação de todos os membros dos grupo é fundamental, devendo cooperar na observação e comparação entre as medidas realizadas. Durante a realização da atividade é importante observar as dificuldades apresentada.
Questione os alunos estimulando-os:
- O que é mais importante, os valores das medidas encontrados ou a comparação entre esses valores?
- Como são os lados destes quadriláteros? São iguais? São diferentes? São paralelos?
- Vamos comparar os quadriláteros? (o quadrado com o retângulo; o quadrado com o losango; o quadrado com o paralelogramo etc);
- O que percebemos ao comparar os ângulos formados nos cruzamentos da diagonais?
Propósito: Compreender que alguns quadriláteros podem pertencer a diversas classes em virtude de suas características que se interconectam, conseguindo classificá-los em grupos distintos ou iguais.
Materiais complementares:
Atividade principal
Resolução atividade principal
Guia de intervenção
Analisando as soluções
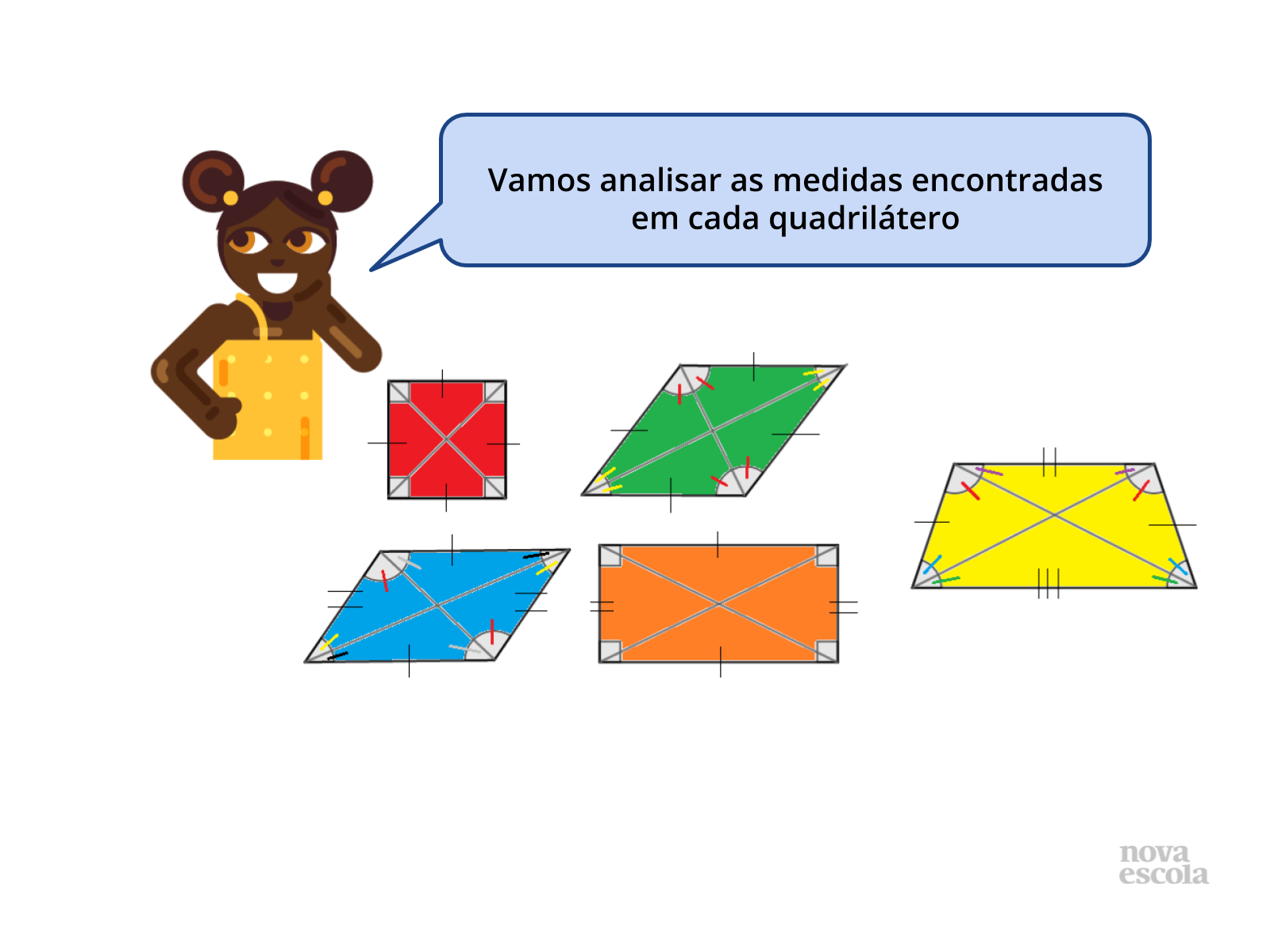
Tempo sugerido: 6 minutos (slides 5 a 7).
Orientações: A análise das soluções será feita com a participação dos grupos, onde cada grupo irá apresentar os resultados de suas medições dos lados, ângulos e diagonais dos quadriláteros.
Observação: não coloquei as medidas dos lados, pois poderão ocorrer discrepâncias no material impresso. No entanto é bom o professor confirmar as medidas dos ângulos internos, no slide os identifiquei com traços coloridos, onde cores iguais representam ângulos iguais. Para acessar o documento com os valores dos ângulos e solução clique (aqui).
Pergunte aos grupos:
- Qual desses quadriláteros poderia ser separado dos demais em virtude de suas diferenças acentuadas?
Propósito: Reconhecer o trapézio como um quadrilátero com características diferentes dos demais, já que possui três lados com medidas diferentes, um par de lados opostos não paralelos e suas diagonais não se interceptam em seus pontos médios.
Analisando as soluções
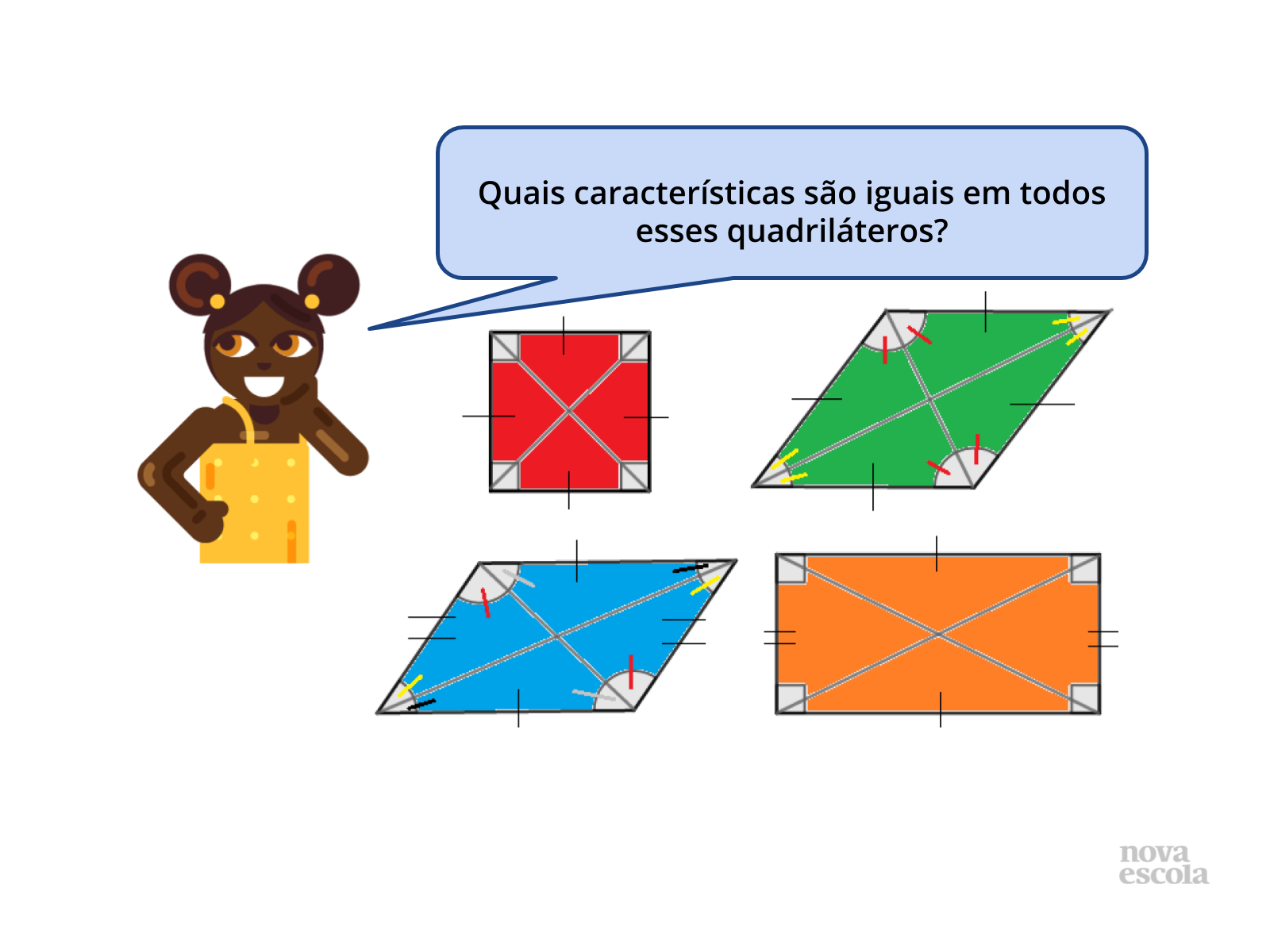
Tempo sugerido: 6 minutos (slides 5 a 7).
Orientações: Peça para os alunos focar em características comuns e não nas diferenças entre os pares de lados
Pergunte aos grupos:
- Quando as diagonais se cruzam, o que percebemos sobre suas metades?
- As distâncias entre os lados opostos é igual (no sentido de paralelos)?
- O que percebemos sobre os ângulos opostos?
Propósito: Entender que todos esses quadriláteros possuem várias características em comum e todos possuem lados opostos paralelos. Por essa razão podem ser considerados pertencentes a uma mesma classe (paralelogramos).
Analisando as soluções

Tempo sugerido: 6 minutos (slides 5 a 7).
Orientações: Questionar os alunos de maneira que eles percebam que as próprias respostas estão sendo levadas em consideração na obtenção do conhecimento da classe em geral, onde o resultado vem do esforço dos alunos em responder os questionamentos do professor.
Pergunte aos grupos:
- Com relação aos ângulos como são as figuras comparadas?
- Com relação aos lados como são as figuras comparadas?
- Qual ângulo formado pelas diagonais quando se interceptam?
- Desses quadriláteros apresentados qual deles possui mais características em comum com os demais?
Propósito: Destacar o quadrado como possuidor de várias semelhanças tanto com o losango, o retângulo e o paralelogramo. Compreender com isso que o quadrado também é retângulo, losango. e paralelogramo.
Encerramento
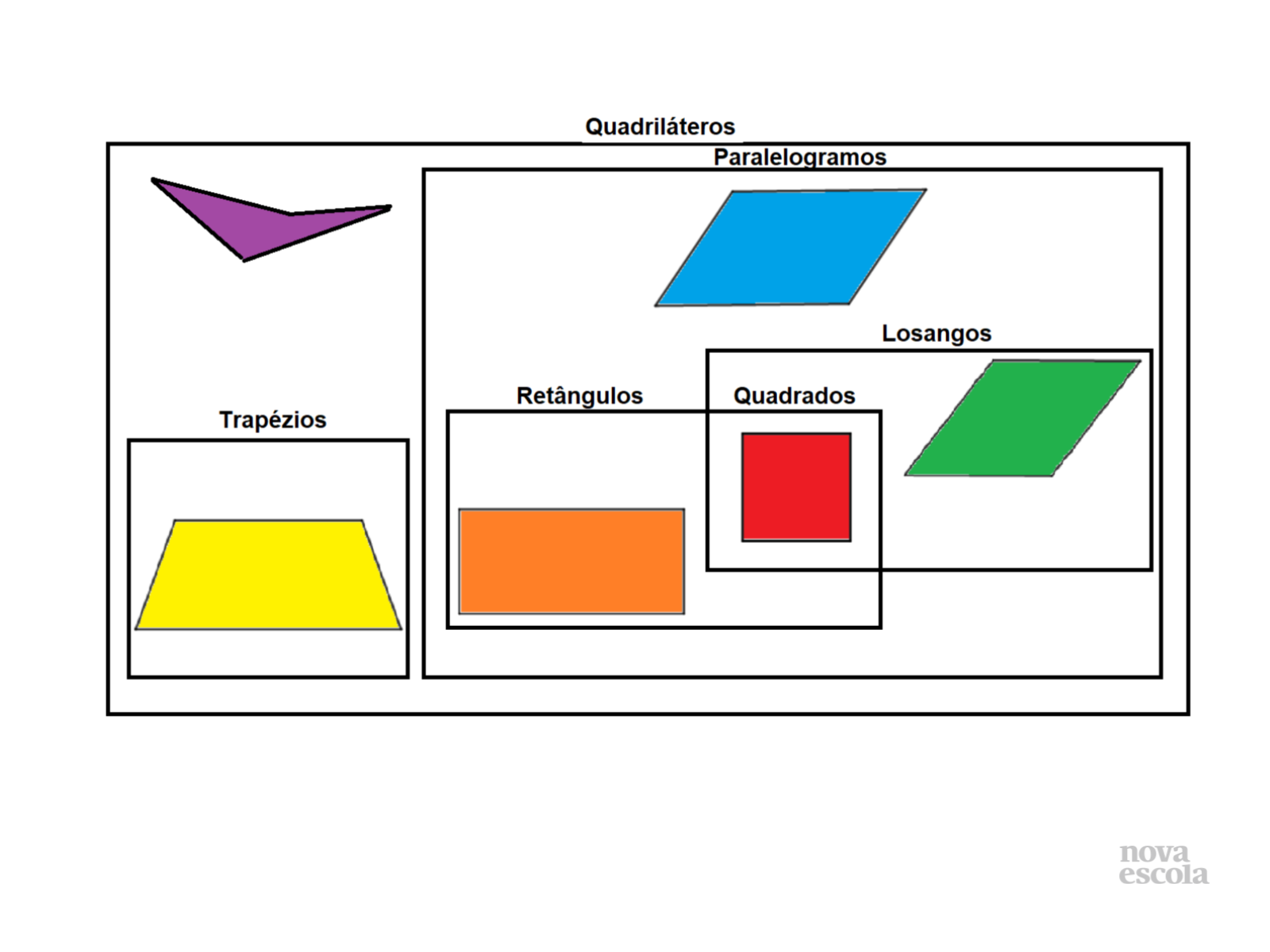
Tempo sugerido: 6 minutos
Orientações: Converse com a classe sobre os objetivos pretendidos e confirme que foram alcançados questionando os alunos sobre o que aprenderam durante a realização e correção da atividade principal. Converse com os alunos usando o slide. Diga por exemplo: Conseguem perceber que o quadrado além de quadrilátero também é losango, retângulo e paralelogramo.
Questione os alunos:
- Por que o quadrilátero roxo está separado dos demais?
- O que falta no trapézio para fazer parte dos paralelogramos?
- Quais características o quadrado possui para fazer parte de três classes de quadriláteros?
Propósito: Compreender as características dos quadriláteros para sua identificação e entender que existe a intersecção entre as classes.