Atividade principal
Plano de Aula
Plano de aula: E agora? Como atravessar?
Plano 8 de uma sequência de 10 planos. Veja todos os planos sobre Processos Matemáticos
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Esther Maria Freixedelo Martins
Mentora: Edicléia Xavier da Costa
Especialista: Rita Batista
Habilidade da BNCC
Desenvolver estratégias de representação de um problema não convencional e comparar diferentes soluções para uma mesma situação-problema.
Objetivos específicos
- Resolver problemas de travessia, considerando o estado inicial, o estado final e as restrições apresentadas na situação.
- Resolver problema de lógica, contendo dados não numéricos.
- Compreender o texto do problema, utilizando o raciocínio lógico para chegar à solução.
- Utilizar e representar estratégias diversas de resolução.
Conceito-chave
Resolução de problemas de lógica com a ideia de travessia.
Recursos necessários
Quadro, giz, lápis, borracha, cópias das atividades principais e raio-x ou projetor de slides, computador ou datashow para projeção da apresentação.
Habilidades BNCC:
Objetivos de aprendizagem
- Resolver problemas de travessia, considerando o estado inicial, o estado final e as restrições apresentadas na situação.
- Resolver problema de lógica, contendo dados não numéricos.
- Compreender o texto do problema, utilizando o raciocínio lógico para chegar à solução.
- Utilizar e representar estratégias diversas de resolução.
Resumo da aula
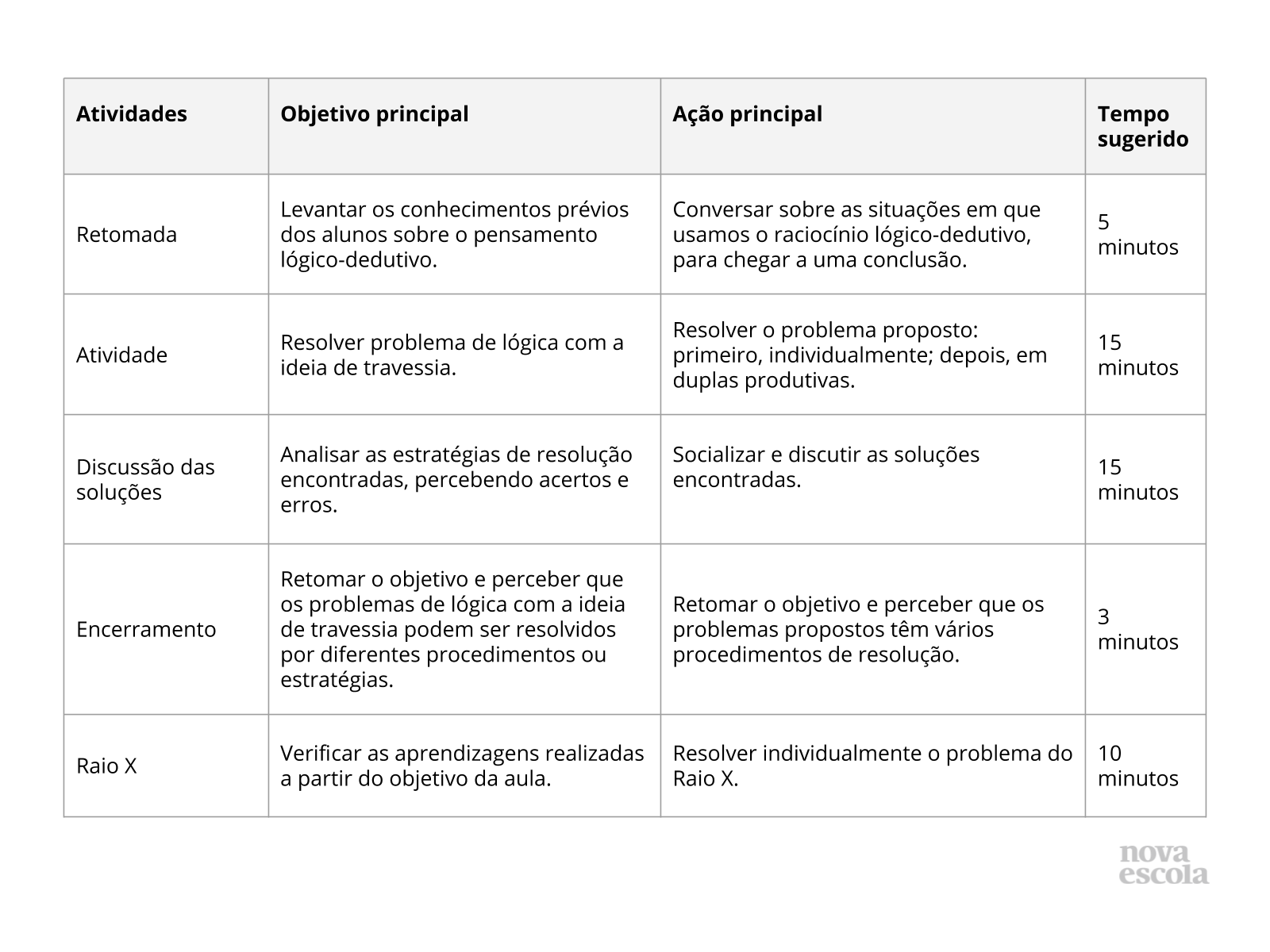
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Propósito:
Compartilhar o objetivo da aula com os alunos, explicando seus termos.
Tempo sugerido: 2 minutos
Orientação: Professor(a), escreva o objetivo na lousa ou apresente-o, usando um computador ou datashow.
Leia o objetivo com seus alunos e comente que os problemas de lógica são aqueles que precisam ser resolvidos por processos matemáticos.
Explore o significado das palavras “travessia” e “atravessar”, como ir de um lugar para o outro ou sair de um estado inicial para um estado final.
Realize o aquecimento, logo a seguir.
Aquecimento

Propósito: Refletir sobre o objetivo da aula. Aguçar a curiosidade dos alunos para os problemas de travessia.
Tempo sugerido: 5 minutos
Orientação: Professor(a), leia as estrofes do poema em voz alta, dando ritmo e expressividade à leitura.
Discuta com a turma:
- Você conhece algum problema ou jogo de travessia? Fale sobre isso.
- Como é o problema “Milho, galinha e raposa”? Por que é preciso levar uma coisa de cada vez?
- Por que o problema “parece bem simples, mas tem certas condições”?
- O que significa ser ”um problema antigo, que vem de longa tradição”?
(Ver mais orientações no arquivo: resolução da atividade de aquecimento).
Materiais complementares:
Resolução atividade aquecimento
Aquecimento
Propósito: Refletir sobre o objetivo da aula. Aguçar a curiosidade dos alunos para os problemas de travessia.
Tempo sugerido: 5 minutos
Orientação: Professor(a), leia as estrofes do poema em voz alta, dando ritmo e expressividade à leitura.
Discuta com a turma:
- Você conhece algum problema ou jogo de travessia? Fale sobre isso.
- Como é o problema “Milho, galinha e raposa”? Por que é preciso levar uma coisa de cada vez?
- Por que o problema “parece bem simples, mas tem certas condições”?
- O que significa ser ”um problema antigo, que vem de longa tradição”?
(Ver mais orientações no arquivo: resolução da atividade de aquecimento).
Atividade Principal

Propósito:
Permitir que os alunos busquem suas próprias soluções, individualmente e na troca com seus pares, realizando o esforço produtivo necessário à aprendizagem.
Tempo sugerido: 15 minutos
Orientação: Pedir que os alunos leiam e resolvam o problema individualmente. Depois de 5 minutos, organize os alunos em duplas produtivas, para que possam trocar ideias e comparar suas estratégias de resolução.
Discuta com a turma: Nesse momento o professor deve intervir nas duplas apenas para determinar o que os alunos estão pensando e oferecer ideias baseadas no pensamento dos alunos, sem redirecionar para estratégias diferentes.
Materiais complementares:
Discussão da solução

Tempo sugerido:15 minutos.
Propósito:
Compartilhar as soluções produzidas pelos alunos, para que possam compará-las, percebendo semelhanças e diferenças, discutir as estratégias e definir as que estão certas e as que apresentam algum equívoco.
Orientação: Escolha alguns alunos para que expliquem aos demais colegas como pensaram e peça que compartilhem suas soluções, registrando na lousa o resultado obtido por cada dupla, além de identificar os nomes das duplas abaixo dos registros.
Pergunte aos demais alunos se alguém pensou de maneira diferente dos colegas e deixe que os alunos expliquem suas descobertas, mesmo que não estejam corretas.
Discuta com a turma:
- No que precisamos pensar para resolver esse desafio?
- A travessia pode ser feita de qualquer jeito ou há “condições” ou “obstáculos” que devem ser considerados na solução?
- É possível descobrir a resposta sem usar um registro?
- Quem poderia compartilhar sua solução na lousa?
- Todos resolveram da mesma forma? Quem pode apresentar uma solução diferente?
- A resposta foi a mesma nas duas soluções apresentadas? Por quê?
Discussão da solução
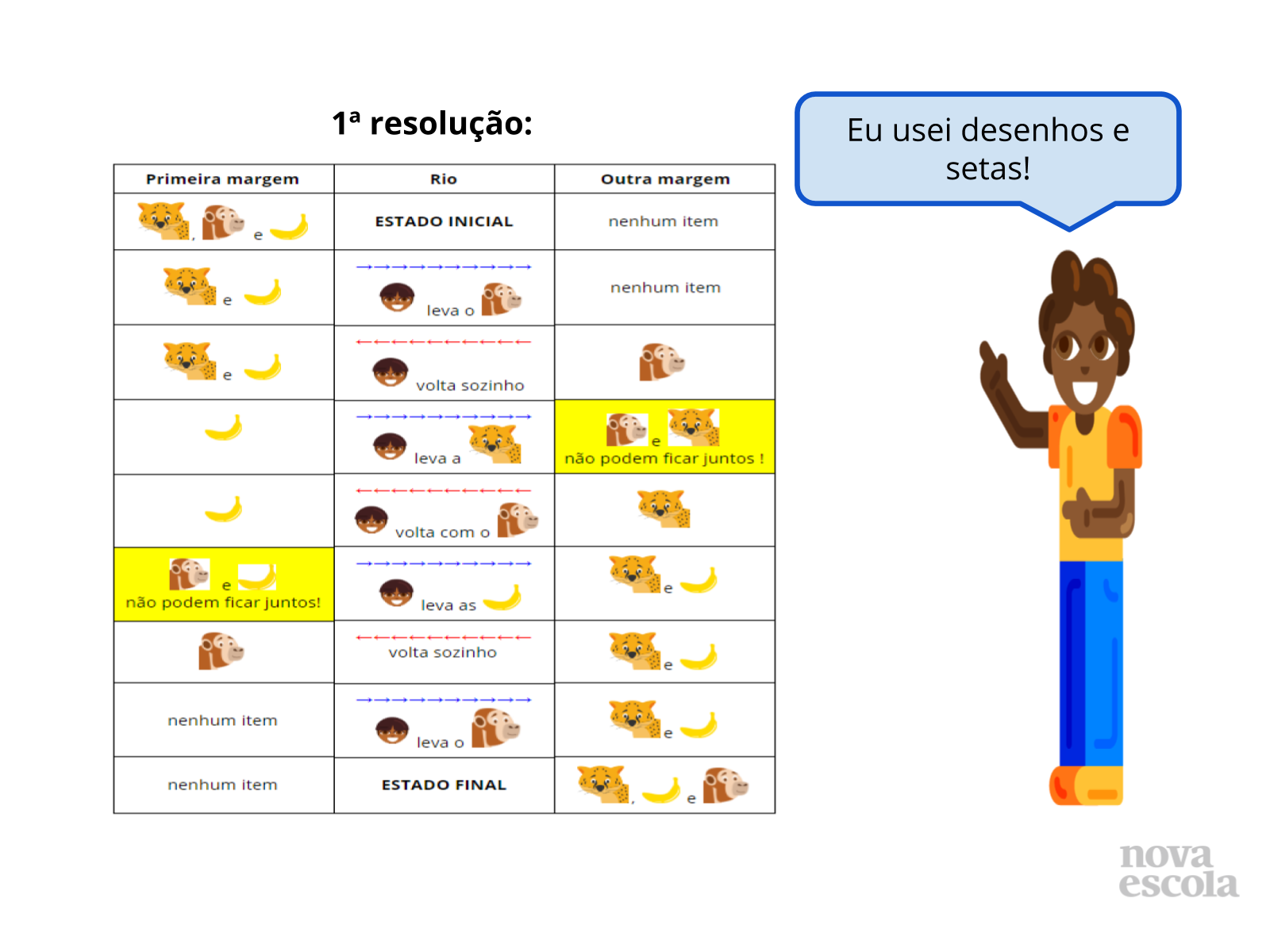
Tempo sugerido:15 minutos.
Propósito:
Compartilhar as soluções produzidas pelos alunos, para que possam compará-las, percebendo semelhanças e diferenças, discutir as estratégias e definir as que estão certas e as que apresentam algum equívoco.
Orientação: Escolha alguns alunos para que expliquem aos demais colegas como pensaram e peça que compartilhem suas soluções, registrando na lousa o resultado obtido por cada dupla, além de identificar os nomes das duplas abaixo dos registros.
Pergunte aos demais alunos se alguém pensou de maneira diferente dos colegas e deixe que os alunos expliquem suas descobertas, mesmo que não estejam corretas.
Discuta com a turma:
- Há um único jeito de resolver esse problema ou vários?
- Essas soluções diferentes estão corretas ou só uma delas é a certa?
- Essa solução se parece com as que foram apresentadas pelos colegas da nossa classe? Por quê?
- Qual das soluções é mais fácil de compreender?
Discussão da solução

Tempo sugerido:15 minutos.
Propósito:
Compartilhar as soluções produzidas pelos alunos, para que possam compará-las, percebendo semelhanças e diferenças, discutir as estratégias e definir as que estão certas e as que apresentam algum equívoco.
Orientação: Escolha alguns alunos para que expliquem aos demais colegas como pensaram e peça que compartilhem suas soluções, registrando na lousa o resultado obtido por cada dupla, além de identificar os nomes das duplas abaixo dos registros.
Pergunte aos demais alunos se alguém pensou de maneira diferente dos colegas e deixe que os alunos expliquem suas descobertas, mesmo que não estejam corretas.
Discuta com a turma:
- Há um único jeito de resolver esse problema ou vários?
- Essas soluções diferentes estão corretas ou só uma delas é a certa?
- Essa solução se parece com as que foram apresentadas pelos colegas da nossa classe? Por quê?
- Qual das soluções é mais fácil de compreender?
Discussão da solução

Tempo sugerido:15 minutos.
Propósito:
Compartilhar as soluções produzidas pelos alunos, para que possam compará-las, percebendo semelhanças e diferenças, discutir as estratégias e definir as que estão certas e as que apresentam algum equívoco.
Orientação: Escolha alguns alunos para que expliquem aos demais colegas como pensaram e peça que compartilhem suas soluções, registrando na lousa o resultado obtido por cada dupla, além de identificar os nomes das duplas abaixo dos registros.
Pergunte aos demais alunos se alguém pensou de maneira diferente dos colegas e deixe que os alunos expliquem suas descobertas, mesmo que não estejam corretas.
Discuta com a turma:
- Há um único jeito de resolver esse problema ou vários?
- Essas soluções diferentes estão corretas ou só uma delas é a certa?
- Essa solução se parece com as que foram apresentadas pelos colegas da nossa classe? Por quê?
- Qual das soluções é mais fácil de compreender?
Discussão da solução

Tempo sugerido:15 minutos.
Propósito:
Compartilhar as soluções produzidas pelos alunos, para que possam compará-las, percebendo semelhanças e diferenças, discutir as estratégias e definir as que estão certas e as que apresentam algum equívoco.
Orientação: Escolha alguns alunos para que expliquem aos demais colegas como pensaram e peça que compartilhem suas soluções, registrando na lousa o resultado obtido por cada dupla, além de identificar os nomes das duplas abaixo dos registros.
Pergunte aos demais alunos se alguém pensou de maneira diferente dos colegas e deixe que os alunos expliquem suas descobertas, mesmo que não estejam corretas.
Discuta com a turma:
- Há um único jeito de resolver esse problema ou vários?
- Essas soluções diferentes estão corretas ou só uma delas é a certa?
- Essa solução se parece com as que foram apresentadas pelos colegas da nossa classe? Por quê?
- Qual das soluções é mais fácil de compreender?
Discussão da solução

Tempo sugerido:15 minutos.
Propósito:
Compartilhar as soluções produzidas pelos alunos, para que possam compará-las, percebendo semelhanças e diferenças, discutir as estratégias e definir as que estão certas e as que apresentam algum equívoco.
Orientação: Escolha alguns alunos para que expliquem aos demais colegas como pensaram e peça que compartilhem suas soluções, registrando na lousa o resultado obtido por cada dupla, além de identificar os nomes das duplas abaixo dos registros.
Pergunte aos demais alunos se alguém pensou de maneira diferente dos colegas e deixe que os alunos expliquem suas descobertas, mesmo que não estejam corretas.
Discuta com a turma:
- Há um único jeito de resolver esse problema ou vários?
- Essas soluções diferentes estão corretas ou só uma delas é a certa?
- Essa solução se parece com as que foram apresentadas pelos colegas da nossa classe? Por quê?
- Qual das soluções é mais fácil de compreender?
Encerramento
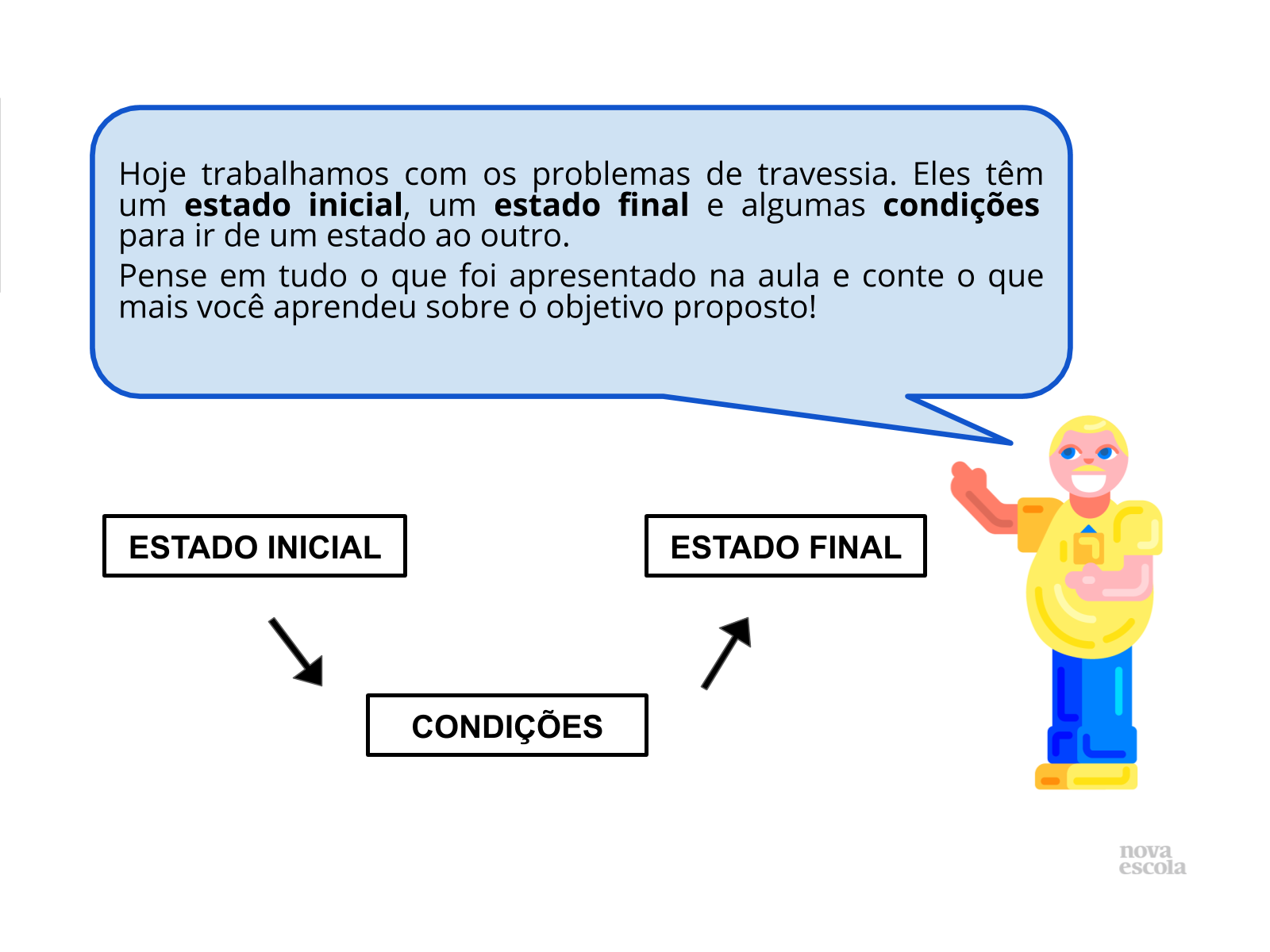
Tempo sugerido: 3 minutos
Orientação: Permita que alguns alunos expliquem o que aprenderam durante a aula, articulando suas ideias com o objetivo apresentado.
Discuta com a turma: Foque a atenção dos alunos para o objetivo da aula e para a retomada do que foi realizado.
Os alunos, provavelmente, vão pontuar que os problemas de lógica com a ideia de travessia contam uma história, que é preciso prestar atenção nas condições para atravessar, que é preciso ficar indo e voltando com os itens que queremos atravessar, que o registro é muito importante para chegar à solução e que pode ser feito de várias maneiras diferentes.
Propósito: Permitir que o aluno fale sobre o que aprendeu, para estruturar seu pensamento.
Sugestões para o professor:
- Travessias difíceis, divisões divertidas e quadrados mágicos: evolução histórica de três recreações matemáticas. Josinalva Estácio Menezes. - http://www.sbembrasil.org.br/files/viii/pdf/05/5CC19453574449.pdf
- Travessias - http://mj-matemagia.blogspot.com.br/2013/12/travessias.html
- Trabalhe com lógica de um jeito mais divertido - https://novaescola.org.br/conteudo/7137/trabalhe-com-logica-de-um-jeito-mais-divertido
- Problemas matemáticos sem problemas - https://novaescola.org.br/conteudo/2730/problemas-matematicos-sem-problemas
- “Ler, escrever e resolver problemas: habilidades básicas para aprender Matemática” - Kátia Stoccco Smole, Maria Ignez Diniz (organizadoras) - Porto Alegre: Artmed, 2007.
Raio-X

Tempo sugerido: 10 minutos
Orientação: Peça que os alunos, individualmente, leiam a atividade e a realizem, para que você possa verificar a aprendizagem realizada.
Propósito: Avaliar a aprendizagem realizada para poder planejar as próximas aulas.
Materiais complementares:
Resolução atividade complementar
Sugestão de adaptação para ensino remoto
Código do plano
MAT4_28RDP_08
Recursos
- Necessários: Caderno e lápis.
- Opcionais: - Atividades impressas;
- Algum meio de comunicação: Zoom, Google Meet, Team Link, WhatsApp, e-mail.
Para este plano, a sugestão é que foque na atividade principal, lembrando a importância de visitar todas as etapas do plano, para assim poder identificar outras partes que julgue relevante para contribuir com a aprendizagem de seus alunos.
Atividade principal
A atividade principal apresenta um problema de lógica com a ideia de travessia, com caráter lúdico e desafiador. Dessa forma, a abordagem desse problema, pode ser em aula síncrona ou assíncrona.
Na aula síncrona (Zoom, Google Meet ou Team Link), você pode apresentar o slide 5 e solicitar que os alunos realizem a leitura. Depois estimule uma conversa coletiva sobre as ideias principais apresentadas no problema, para certificar-se que compreenderam a situação proposta. Em seguida, desafie os alunos a solucionarem o problema no caderno. Estabeleça um tempo para realizarem a resolução e aborde com eles alguns questionamentos apresentados no “Discuta com a turma”, por exemplo:
- No que precisamos pensar para resolver esse desafio?
- A travessia pode ser feita de qualquer jeito ou há “condições” ou “obstáculos” que devem ser considerados na solução?
- É possível descobrir a resposta sem usar um registro?
- Há um único jeito de resolver esse problema ou vários?
- Qual das soluções é mais fácil de compreender?
De acordo com as ideias apresentadas pelos alunos, você poderá ser o escriba, tendo o cuidado de registrar, focando a câmera, para que todos possam visualizar. Lembrando de incentivar os alunos a explicarem suas ideias.
Na aula assíncrona, você pode fotografar ou printar a tela do slide 5, e alguns questionamentos que julgar pertinente e compartilhar com os alunos via WhatsApp ou e-mail. Estabelecendo um prazo para a devolutiva da resolução, deixando a possibilidade do contato com você para esclarecimentos necessários.
Se não for possível a comunicação on-line com seus alunos, escolha atividades desse e de outros planos que, juntamente com a apresentada no slide citado, formem uma sequência. Faça a impressão, inclusive com orientações, questionamentos e um cronograma para a realização das mesmas. Solicite às famílias que peguem na escola. Neste caso, acompanhe as aprendizagens sugerindo registros de soluções e/ou a confecção de um “Diário de bordo”. De forma que possa ser estabelecido um acordo para que, se possível, as famílias encaminhem a devolutiva à escola.
Vale ressaltar que a Atividade complementar do plano apresenta problemas que contribuem para o desenvolvimento da aprendizagem dos estudantes.
Discussão das soluções
Na aula síncrona, o problema pode ser respondido no caderno e as resoluções socializadas e discutidas, mesmo as que apresentam equívoco, mediante questionamentos e incentivo do(a) professor(a) para que o aluno explique seu raciocínio. Importante, provocar reflexões com as perguntas sugeridas no “Discuta com a turma”.
Na aula assíncrona, as resoluções devem ser devolvidas ao professor de acordo com o meio de entrega (digital ou físico). No caso da devolutiva digital, o professor pode favorecer a socialização das resoluções apresentadas pelos alunos, através de fotos, mensagem de texto ou áudio. Entretanto, na devolutiva física, o professor deve organizar as soluções e explicações apresentadas e encaminhar para os estudantes que recorrem a este meio de comunicação.
Sistematização
De acordo com o meio de comunicação estabelecido para abordar as atividades, favorecer, através da socialização dos raciocínios apresentados, o reconhecimento de que para solucionar problemas de lógica com a ideia de travessia, é preciso considerar o estado inicial e as condições dadas para assim, chegar ao estado final, e dessa forma, o aluno estabelecerá as etapas da travessia.
Pode ser oportunizada a leitura do texto apresentado no encerramento (slide 12) para maior apropriação dos conceitos abordados nas atividades.
Raio X
A atividade do Raio X apresentada no slide 13 pode ser usada para verificar se os alunos solucionam problemas de lógica com a ideia de travessia.
Dessa forma, professor, trabalhe esse problema, pelo mesmo meio de comunicação adotado para a realização da atividade principal, ressaltando a importância de você realizar a análise das respostas apresentadas por cada estudante e quando possível possibilitar a discussão das mesmas.
Convite às famílias
Oriente aos familiares que nesse momento é ideal que estabeleçam a rotina de estudo para seu/sua filho(a), com horários definidos. Relembre-os da importância de incentivar e se possível acompanhar as atividades do seu/sua filho(a).
Sugira que os alunos, na busca de estruturar seu pensamento, socializem com seus familiares o que aprenderam nesta aula.
Se eles tiverem acesso à internet, compartilhe com eles os link desse jogo de travessia:
https://rachacuca.com.br/jogos/o-lobo-e-a-ovelha/
Este pode ser um momento muito relevante de interação na família, e de grande aprendizado.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Esther Maria Freixedelo Martins
Mentora: Edicléia Xavier da Costa
Especialista: Rita Batista
Habilidade da BNCC
Desenvolver estratégias de representação de um problema não convencional e comparar diferentes soluções para uma mesma situação-problema.
Objetivos específicos
- Resolver problemas de travessia, considerando o estado inicial, o estado final e as restrições apresentadas na situação.
- Resolver problema de lógica, contendo dados não numéricos.
- Compreender o texto do problema, utilizando o raciocínio lógico para chegar à solução.
- Utilizar e representar estratégias diversas de resolução.
Conceito-chave
Resolução de problemas de lógica com a ideia de travessia.
Recursos necessários
Quadro, giz, lápis, borracha, cópias das atividades principais e raio-x ou projetor de slides, computador ou datashow para projeção da apresentação.

















